ПРЯМОУГОЛЬНАЯ ДИМЕТРИЧЕСКАЯ ПРОЕКЦИЯ. Косоугольная диметрическая проекция

Косоугольная диметрическая проекция

Эта проекция косоугольная, следовательно, проецирующие лучи составляют с картинной плоскостью угол отличный от прямого. И, она – диметрическая, значит оси X и Z отклонены от картины на одинаковый (небольшой) угол. И коэффициенты искажения по этим осям одинаковые. А ось Y отклонена от картины на значительный угол и, следовательно, имеет другой коэффициент искажения. ГОСТ 2.317-69 разрешает следующее расположение осей координат: ось X – горизонтальна, ось Z – вертикальна, а ось Y – отклонена от горизонтали на 45о. Устанавливаются следующие приведенные коэффициенты искажения вдоль:

- оси X – 1, k = 1

- оси Z – 1, n = 1

- оси Y – 1, m = 0,5 (то есть размеры, расположенные вдоль этой оси нужно уменьшать вполовину).

Безусловно, необходимость пересчитывать размеры составляет некоторое неудобство, что вполне искупается тем, что при проецировании на фронтальную плоскость сохраняются не только линейные, но и угловые размеры. Это значит, что плоские фигуры параллельные фронтальной плоскости проецируются на нее в натуральную форму, то есть без искажения. Например, окружность проецируется на фронтальную плоскость, как окружность.

На горизонтальную и профильную плоскости проекций окружности проецируются, как эллипсы. При проецировании на горизонтальную плоскость проекций большая ось эллипса отклонена от горизонтали в сторону оси X на угол 7о14′. При проецировании на профильную плоскость проекций большая ось эллипса отклонена от вертикали в сторону оси Z на угол 7о14′. Такой угол определяется из прямоугольного треугольника с соотношением сторон 8 : 1(рис. 96).

Коэффициенты искажения по осям

AB = 1,07 d

CD ┴ AB,CD = 0,33 d

Для горизонтальной проекции:

KL // OX,KL = 1 d

MN //OY, MN = 0,5d

Для профильной проекции:

KL // OZ,KL = 1 d

MN //OY, MN = 0,5 d

Прямоугольная диметрическая проекция

Из всех трех рассматриваемых аксонометрических проекций прямоугольная диметрия наиболее трудоемка, однако, считается, что она наиболее наглядна (рис. 97).

Для этой проекции приняты следующее расположение осей координат и приведенные коэффициенты искажения:

– ось X отклонена от горизонтали на угол 7о10′. Такой угол с достаточной точностью определяется из прямоугольного треугольника с соотношением катетов 8 : 1. Приведенный коэффициент искажения – k = 1,

–осьY отклонена от горизонтали на угол 41о25′. Такой угол строится в прямоугольном треугольнике с соотношением сторон 8 : 7. приведенный коэффициент искажения – m = 0,5,

– ось Z направлена вертикально. Приведенный коэффициент искажения – n = 1.

На все три плоскости проекций окружности проецируются, как эллипсы.

При проецировании на горизонтальную плоскость проекций:

– большая ось эллипса AB расположена горизонтально.

AB = 1,06 d,

– малая ось CD перпендикулярна AB. CD = 0,35 d,

– сопряженный диаметр KL // OX. KL = 1 d,

– сопряженный диаметр MN // OY. MN = 0,5 d.

При проецировании на профильную плоскость проекций:

– большая ось эллипса AB расположена перпендикулярно оси X. AB = 1,06 d,

– малая ось CD перпендикулярна AB. CD = 0,35 d,

– сопряженный диаметр KL // OZ. KL = 1 d,

– сопряженный диаметр MN // OY. MN = 0,5 d.

При проецировании на фронтальную плоскость проекций:

– большая ось эллипса AB расположена перпендикулярно оси Y. AB = 1,06 d,

– малая ось CD перпендикулярна AB. CD = 0,95 d,

– сопряженный диаметр KL // OX. KL = 1 d,

– сопряженный диаметр MN // OZ. MN = 1 d.

ТЕХНИЧЕСКОЕ РИСОВАНИЕ

Техническое рисование – это способ наглядного изображения предметов «от руки». Без применения инструментов в глазомерном масштабе. Технический рисунок должен адекватно передавать форму предмета и пропорциональность его частей.

Технический рисунок является обязательной стадией разработки дизайн-проектов, и совершенно необходим в процессе обучения большой части дисциплин.

stydopedya.ru

Прямоугольная диметрия

В прямоугольной диметрической проекции натуральные коэффициенты искажения следующие имеют значение:

Приведенные коэффициенты:.

В прямоугольной диметрии ось z располагается вертикально. Угол между линией горизонта (рис. 2.2) и осью x составляет 710, а между линией горизонта и осью y - 4125.

Для построения угла, приблизительно равного 710, строят прямоугольный треугольник, катеты которого составляют одну и восемь единиц; для построения угла, приблизительно равного 4125, строят прямоугольный треугольник с катетами семь и восемь единиц.

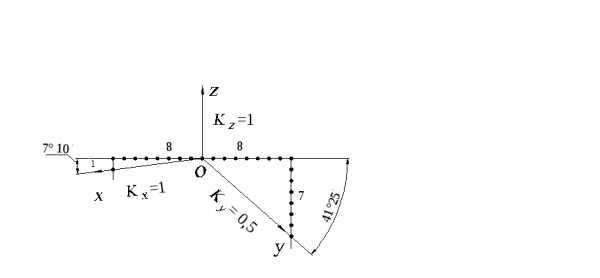
Рис. 2.2

Косоугольная фронтальная изометрия

В косоугольной фронтальной изометрии приведенные коэффициенты искажения равны по всем осям.

В косоугольной фронтальной изометрии ось z располагается вертикально (рис. 2.3), угол между осями z и x составляет 90, а между линией горизонта и осью y - 45(допускается проводить ось y под углом 30 или 60).

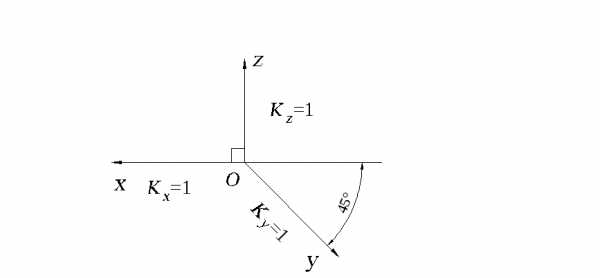
Рис. 2.3

Косоугольная фронтальная диметрия

В косоугольной фронтальной диметрии приведенные коэффициенты равны:

Расположение осей следующее (рис. 2.4): ось z располагается вертикально, угол между осями z и x составляет 90, а между линией горизонта и осью y - 45 (допускается проводить ось y под углом 30 или 60).

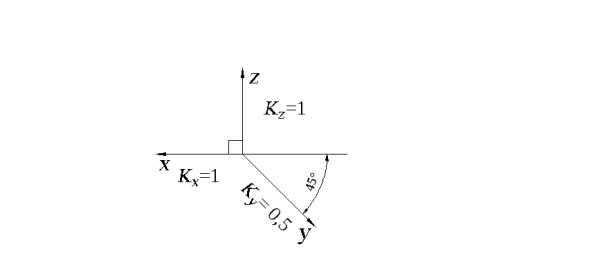
Рис. 2.4.

Косоугольная горизонтальная изометрия

В косоугольной горизонтальной изометрии приведенные коэффициенты искажения равны по всем осям:

Расположение осей следующее (рис. 2.5): ось z располагается вертикально, угол между осями x и y составляет 90º, а угол между линией горизонта и осью y составляет 30º (допускается проводить ось y под углом 45º или 60º).

Рис. 2.5.

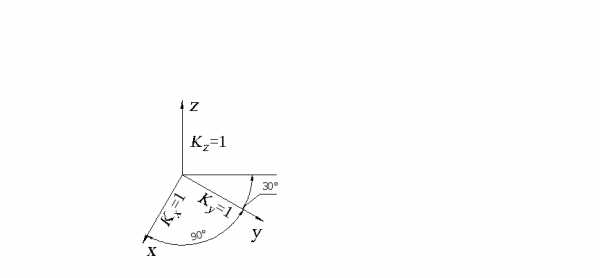
Линии штриховки сечений наносят параллельно одной из диагоналей проекций квадратов (рис. 2.6), лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям.

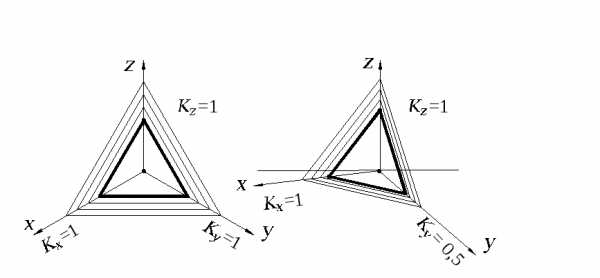
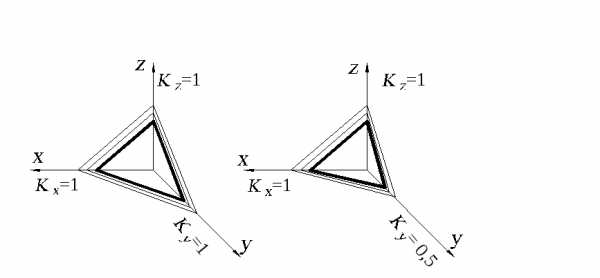
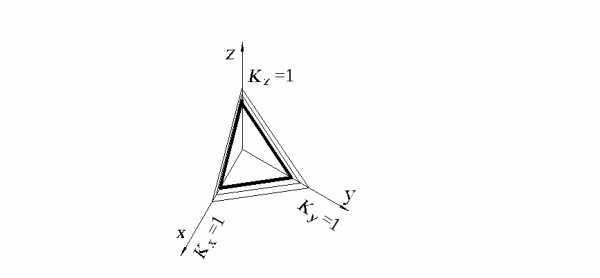
Рис. 2.6.

При нанесении размеров в аксонометрических проекциях выносные линии проводят параллельно аксонометрическим осям, размерные – параллельно измеряемому отрезку.

Порядок выполнения наглядного изображения призмы

1. Выбрать соответствующую аксонометрическую проекцию. Призму, в основании которой лежит правильный треугольник, пятиугольник или шестиугольник следует выполнить в прямоугольной изометрии или диметрии. Призму, в основании которой лежит четырехугольник следует выполнить в прямоугольной диметрии.

2. Построить аксонометрические оси и изображение плоской фигуры основания в аксонометрии (рис. 2.8, а).

3. Выполнить основные контуры призмы (рис. 2.8, б).

4. Нанести линии уступов и углублений горизонтальных вырезов призмы (рис.2.8, в).

5. Построить вертикальное цилиндрическое отверстие. В прямоугольной аксонометрии окружности вычерчиваются в виде эллипсов (рис. 2.8, г). При вычерчивании эллипсов следует предварительно построить их главные оси (большую и малую). Затем построить окружность исходного диаметра. Следующим этапом в построении является нахождение центров большого и малого радиусов. Пересечение вспомогательной окружности исходного диаметра с малой осью эллипса дает центры О1 и О2. Точки А, B, С, D – точки пересечения исходной окружности с осями проекций. Соединяем центры O1и O2 c точками B и D. Полученными радиусами проводим дуги BC и AD. На пересечении радиусов с большой осью эллипса получим центры О3 и О4 малого радиуса. Проводим еще две дуги AB и CD радиусом O3B = O4C (рис. 2.9).

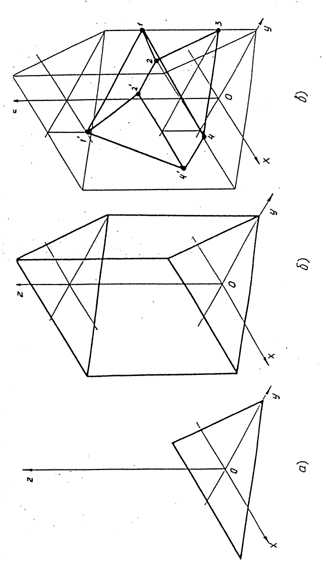
Рис. 2.8

Рис. 2.9

Рис. 2.10

При вычерчивании эллипсов в диметрической прямоугольной проекции следует начинать с вычерчивания осей. Затем необходимо построить окружность исходного диаметра и из центра О в обе стороны по вертикали отложить расстояние, равное диаметру заданной окружности, получаем новые центры О1 и О2. Точки А, B, С, D – точки пересечения исходной окружности с осями проекций. Соединяем центр О1 с точкой D, а центр О2 с точкой В, на пересечении этих линий с большой осью эллипса находим еще два новых центра - О3 и О4. Из этих центров проводим: дуги ВС и AD радиусом R = O2B = O1D; дуги AB и CD радиусом r = О3С = О4B (рис. 2.10).

6. Выполнить разрезы и сечения. При построении разрезов секущие плоскости следует проводить параллельно плоскостям, определяемым аксонометрическими осями, т.е. xОy, xОz, yОz. Нанести направление линии штриховки с учетом коэффициентов искажения по аксонометрическим осям (рис. 2.8, д)

7. Обвести чертеж соответствующими линиями (рис. 2.8, е).

8. В правый верхний угол чертежа поместить образец соответствующей аксонометрической проекции. Показать углы наклона аксонометрических осей. Указать коэффициенты искажения и направление штриховки в разрезах и сечениях.

9. Заполнить основную надпись и дополнительную графу.

Пример аксонометрического чертежа призмы показан на (рис. 2.11).

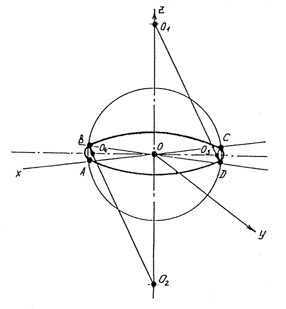
Рис. 2.11

Т е м а 3

studfiles.net

ПРЯМОУГОЛЬНАЯ ДИМЕТРИЧЕСКАЯ ПРОЕКЦИЯ

Расположение осей координат в прямоугольной диметрической проекции показаны на рис 11.6. На практике коэффициенты искажения по осям x и z принимают равным единице, по оси y – 0,5. Таким образом, при построении диметрии вдоль координатных осей x и z откладывают натуральные размеры предмета, а вдоль оси y – в два раза меньше, например, на рис. 11.6 – куб.

Окружности в прямоугольной диметрической проекции показаны на рис. 11.7. В прямоугольной диметрии так же, как в прямоугольной изометрии, большие оси эллипсов всегда располагаются перпендикулярно отсутствующей в данной плоскости аксонометрической оси, а малые оси - параллельны ей.

Рисунок 11.8	Размеры осей эллипсов приведены на рис.11.7, где D – диаметр окружности. На практике эллипс, расположенный в плоскости V (x, z), допускается заменять окружностью. На рис. 11.8 приведено построение овала, заменяющего эллипс, для окружностей, расположенных в плоскостях Н (x, y) и W (y, z). Эти овалы одинаковы по форме и величине. Алгоритм их построения аналогичен построению овала в прямоугольной изометрии. О1 и О2 – центры больших дуг радиусом R, находящиеся на расстоянии D от центра по малой оси.
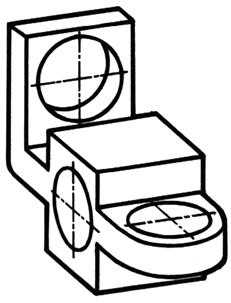Рисунок11.9	Пример изображения детали с отверстиями в изометрии показан на рис.11.9.

КОСОУГОЛЬНАЯ ФРОНТАЛЬНАЯ

ДИМЕТРИЧЕСКАЯ ПРОЕКЦИЯ

Расположение осей координат в косоугольной фронтальной диметрической проекции показаны на рис 11.10. На практике коэффициенты искажения по осям x и z принимают равным единице, по оси y – 0,5 (на рис. 11.10 – куб). Окружности в прямоугольной диметрической проекции показаны на рис. 11.11. Одна из них, расположенная в плоскостиV, проецируется без искажения, две другие - в виде эллипсов (строятся так же, как в прямоуголбной диметрии).

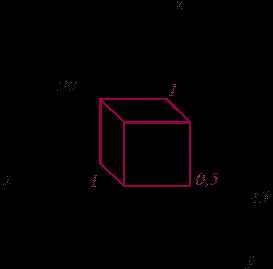Рисунок 11.10

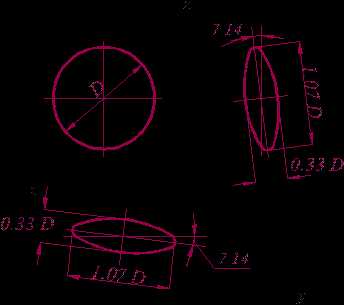Рисунок 11.11

Таким образом, косоугольная фронтальная диметрическая проекция предпочтительна в тех случаях, когда окружности лежат в плоскостях, параллельных плоскости V.

Пример изображения детали с отверстиями в косоугольной фронтальной диметрии показан на рис.11.12.

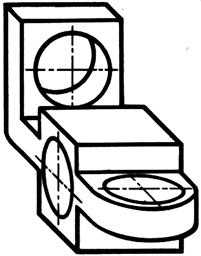
Рисунок11.12

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

1. Для чего используются аксонометрические проекции?

2. Какими свойствами обладают аксонометрические проекции?

3. Какие аксонометрические проекции вы знаете?

4. Как расположены оси координат в прямоугольной изометрической проекции?

5. Какие коэффициенты искажения по осям в прямоугольной изометрической проекции?

6. Как вычерчиваются окружности в аксонометрических проекциях?

7. Как располагаются оси эллипсов в прямоугольной изометрической проекции?

8. Как строят эллипс в прямоугольной изометрической проекции?

9. Как расположены оси координат в прямоугольной диметрической проекции?

10. Какие коэффициенты искажения по осям в прямоугольной диметрической проекции?

11. Как располагаются оси эллипсов в прямоугольной диметрической проекции?

12. Как строят эллипсы в прямоугольной диметрической проекции?

13. Как расположены оси координат в косоугольной фронтальной диметрической проекции?

14. Какие коэффициенты искажения по осям в косоугольной фронтальной диметрической проекции?

15. Как располагаются оси эллипсов в косоугольной фронтальной диметрической проекции?

16. Как строят эллипс в косоугольной фронтальной диметрической проекции?

17. В каких случаях косоугольнаяфронтальная диметрическая проекция предпочтительна?

18. Выберите оси и изображение куба, соответствующие косоугольной фронтальной диметрической проекции. (Ответ: , )

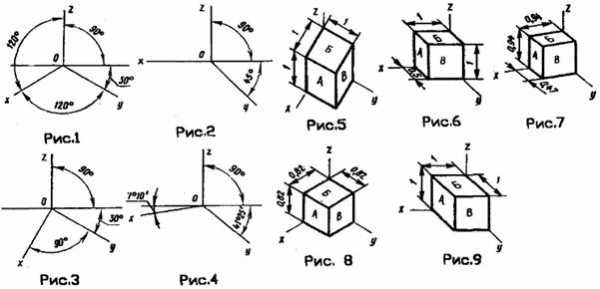
19. Установить соответствие вида аксонометрической проекции и чертежа детали. (Ответ:1-, 2-,3-)

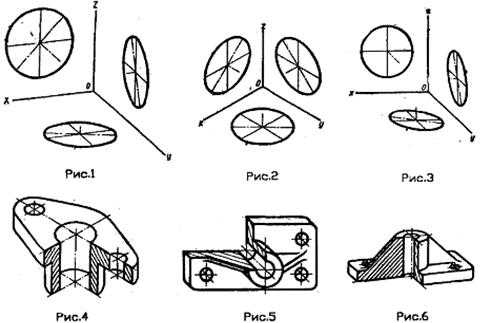
20. В какой аксонометрической проекции изображена деталь?

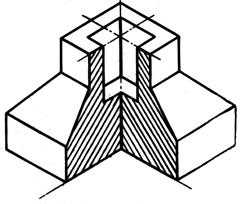
- в прямоугольной изометрии

- в прямоугольной диметрии

- в косоугольной фронтальной диметрии

21. В какой аксонометрической проекции изображена деталь?

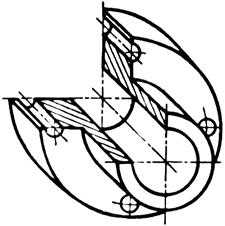
- в прямоугольной изометрии

- в косоугольной фронтальной диметрии

infopedia.su

Диметрическая проекция - это... Что такое Диметрическая проекция?

Диметрическая прое́кция — это аксонометрическая проекция, у которой коэффициенты искажения[1] по двум осям имеют равные значения, а искажение по третьей оси может принимать иное значение.

Стандартные диметрические проекции[2]

Прямоугольная диметрическая проекция

Ось Z' расположена вертикально, а оси X' и Y' образуют с горизонтальной линией углы 7°10' и 41°25'.

Коэффициент искажения по оси Y' равен 0,47, а по осям X' и Z' 0,94. На практике используют приведённые коэффициенты искажения и . В этом случае изображение получается увеличенным в .

Приближённо аксонометрические оси стандартной диметрической проекции можно построить, если принять tg 7°10'=1/8, а tg 41°25'=7/8.

Расположение осей координат в прямоугольной диметрической проекции.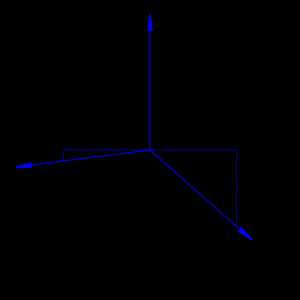

Приближённое построение прямоугольной диметрической проекции.

Фронтальная диметрическая проекция

Расположение осей координат в фронтальной диметрической проекции.

Коэффициент искажения по оси Y' равен 0,5, а по осям X' и Z' 1. Допускается применять фронтальные диметрические проекции с углом наклона оси Y' в 30° и 45°.

Применение

Диметрическая проекция используется в машиностроительном черчении, САПР для построения наглядного изображения детали на чертеже, а также в компьютерных играх для построения трёхмерного изображения.

Примечания

↑ Отношение проекционной длины и действительной длины отрезков параллельных координатным осям
↑ По ГОСТ 2.317-69 — Единая система конструкторской докуметации. Аксонометрические проекции.

Литература

Богданов В. Н., Малежик И. Ф., Верхола А. П. и др. Справочное руководство по черчению. — М.: Машиностроение, 1989. — С. 864. — ISBN 5-217-00403-7
Фролов С. А. Начертательная геометрия. — 2-е изд., перераб. и доп. — М.: Машиностроение, 1983. — С. 240.

dic.academic.ru

Аксонометрические проекции. Прямоугольные изометрия и диметрия. Косоугольная диметрия.

План лекции

1. Коэффициент искажения.

2. Прямоугольная изометрическая проекция.

3. Прямоугольная диметрическая проекция.

4. Косоугольная диметрическая проекция.

При изложении настоящего курса для наглядного изображения расположенных в пространстве относительно выбранных плоскостей проекций точек, линий, плоскостей, многогранников, сечений конической поверхности плоскостями использовались проекции, называемые аксонометрическими (от древнегреческого «аксон» — ось, «метрио» — измеряю) или аксонометрией. Их часто используют для наглядного изображения деталей машин, инструментов на чертеже, особенно на начальных этапах проектирования.

Способ аксонометрического проецирования состоит в том, что данная фигура вместе с осями прямоугольных координат, к которым она отнесена в пространстве, проецируется параллельно на некоторую плоскость, принятую за плоскость аксонометрических проекций (эту плоскость называют также картинной плоскостью).

При параллельном проецировании, если направление проецирования перпендикулярно к аксонометрической плоскости проекций, аксонометрическую проекцию называют прямоугольной, если направление проецирования не перпендикулярно к плоскости проекций, аксонометрическую проекцию называют косоугольной. В прямоугольной аксонометрической проекции оси присоединенных прямоугольных координат располагают непараллельно плоскости аксонометрических проекций.

Применяемые в отечественной конструкторской документации аксонометрические проекции стандартизованы в ГОСТ 2.317-69.

Рассмотрим образование аксонометрической проекции на примере изображения параллелепипеда с квадратным основанием рис. 1 путем последовательного преобразования его ортогональных проекций вместе с осями. При повороте параллелепипеда рис. 1а с осями х и у вокруг оси z по стрелке А на 45° получаем его изображение рис. 1б с повернутыми осями х1 и y1 и сохранившейся вертикальной осью z. При повороте изображения на профильной проекции с осями z", x"1, у"1 по стрелке Б на угол 30° получаем изображение рис. 183в с осями z"1, х"2, y''2, расположенными под некоторыми углами к картинной плоскости P(PW). Параллельная проекция рис. 183г по стрелке В на плоскости Р и является аксонометрической проекцией параллелепипеда с осями на плоскости Р. Аксонометрическую плоскость при этом не обозначают (ею является плоскость бумаги).

а) б)

в) г)

Рис. 1

Проекции осей координат хр, ур, zp на плоскости аксонометрических проекций называют аксонометрическими осями (в дальнейшем индекс «р» будет опускаться).

При различном взаимном расположении осей координат в пространстве и плоскости аксонометрической проекции и при разных направлениях проецирования можно получить множество аксонометрических проекций, отличающихся друг от друга направлением аксонометрических осей и масштабами по ним. Это положение доказано теоремой К. Польке, которая утверждает:три отрезка произвольной длины, лежащие в одной плоскости и выходящие из одной точки под произвольными углами друг к другу, представляют параллельную проекцию трех равных отрезков, отложенных на прямоугольных осях координат от начала.

Рассмотрим направление аксонометрических осей и масштабы по ним для направления проецирования, перпендикулярного аксонометрической плоскости проекций, т. е. для прямоугольной аксонометрической проекции.

Коэффициент искажения

На рисунке 2 изображена пространственная система ортогональных координат Ox, Oy, Oz,единичные отрезки е на осях координат и их проекции в направлении S на некоторую плоскость Р, являющуюся аксонометрической плоскостью проекций. Проекции ех, еу, еz отрезка е на соответствующих аксонометрических осях Орхр, Орур, Opzp в общем случае не равны отрезку е и не равны между собой. Отрезки ех, еу, ez являются единицами измерения по аксонометрическим осям — аксонометрическими единицами (аксонометрическими масштабами).

Отношения

называют коэффициентами искажения по аксонометрическим осям.

В частном случае положение картинной плоскости можно выбрать таким, что аксонометрические единицы — отрезки ех, еу, ez— будут все равны между собой или будет равна между собой пара этих отрезков.

При ех = еу = ez (k = m = n) аксонометрическую проекцию называют изометрической; искажения по всем осям в ней одинаковы. При равенстве аксонометрических единиц по двум осям, обычно при ех = еz ≠ еу (k = n ≠ m),имеем диметрическую проекцию. Если ех ≠ еу ≠ еz, то проекцию называют триметрической.

Картинная плоскость Р на рисунке 185 изображена так, что она пересекает все три координатные оси Ox, Oy, Oz в точках х, у, z соответственно. Рассмотрим прямоугольную аксонометрию. В этом случае отрезок ООр перпендикулярен плоскости Р. Отрезки Орх, Ору, Opz являются аксонометрическими проекциями отрезков Ox, Oy, Oz и представляют собой катеты прямоугольных треугольников,

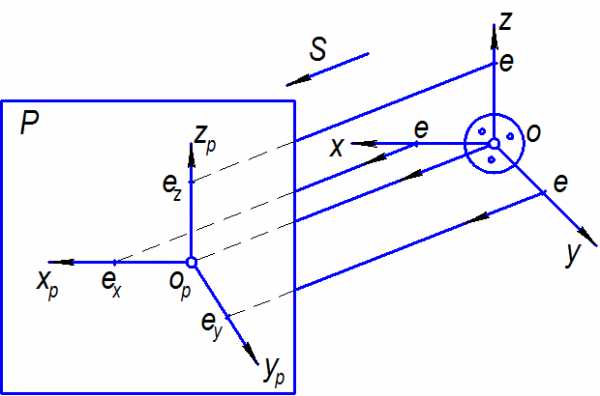
Рис. 2

гипотенузы которых – отрезки Ох, Оу, Oz. Обозначим углы между осями координат и их проекциями на плоскостиР через α, β, γ.Тогда

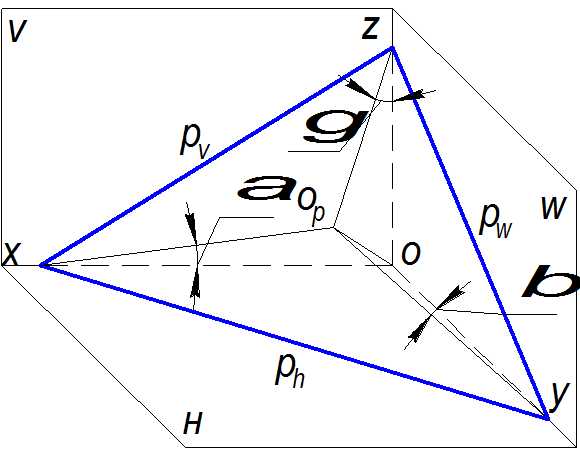
Рис. 3

Эти отношения являются коэффициентами искажения, т. е.

k = cosα; m = cosβ; n = cosγ.

Известно, что для отрезка OOP┴P сумма квадратов направляющих косинусов равна единице:

cos2 (π/2 - α) + cos2 (π/2 - β) + cos2 (π/2 - γ) = 1.

Отсюда

sin2α + sin2β + sin2γ = 1

или

1 – cos2α + 1 – cos2β + 1 – cos2γ = 1.

Тогда

cos2α + cos2β + cos2γ = 2

или

k2 + m2 + n2 = 2,

т. е. сумма квадратов коэффициентов искажения равна 2.

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:

zdamsam.ru

Аксонометрические проекции. Изометрическая проекция - Черчение

Для тoгo чтобы получить аксонометрическую проекцию предмета (рис. 106), необходимо мысленно: поместить предмет в систему координат; выбрать аксонометрическую плоскость проекций и расположить предмет перед ней; выбрать направление параллельных проецирующих лучей, которое не должно совпадать ни с одной из аксонометрических осей; направить проецирующие лучи через все точки предмета и координатные оси до пересечения с аксонометрической плоскостью проекций, получив тем самым изображение проецируемого предмета и координатных осей.

На аксонометрической плоскости проекций получают изображение — аксонометрическую проекцию предмета, а также проекции осей систем координат, которые называют аксонометрическими осями.

Аксонометрической проекцией называется изображение, полученное на аксонометрической плоскости в результате параллельного проецирования предмета вместе с системой координат, которое наглядно отображает его форму.

Система координат состоит из трех взаимно пересекающихся плоскостей, которые имеют фиксированную точку — начало координат (точку О) и три оси (X, У, Z), исходящие из нее и расположенные под прямым углом друг к другу. Система координат позволяет производить измерения по осям, определяя положение предметов в пространстве.

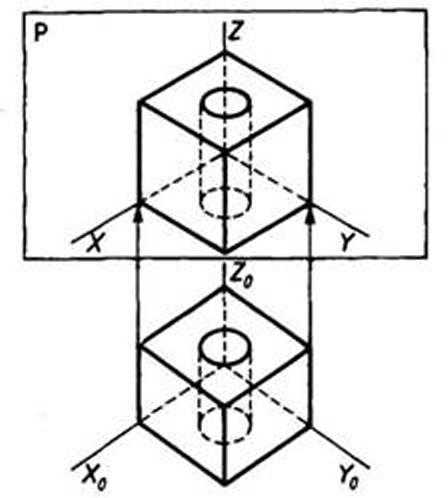
Рис. 106. Получение аксонометрической (прямоугольной изометрической) проекции

Можно получить множество аксонометрических проекций, по- разному располагая предмет перед плоскостью и выбирая при этом различное направление проецирующих лучей (рис. 107).

Наиболее употребляемой является так называемая прямоугольная изометрическая проекция (в дальнейшем будем использовать ее сокращенное название — изометрическая проекция). Изометрической проекцией (см. рис. 107, а) называется такая проекция, у которой коэффициенты искажения по всем трем осям равны, а углы между аксонометрическими осями составляют 120°. Изометрическая проекция получается с помощью параллельного проецирования.

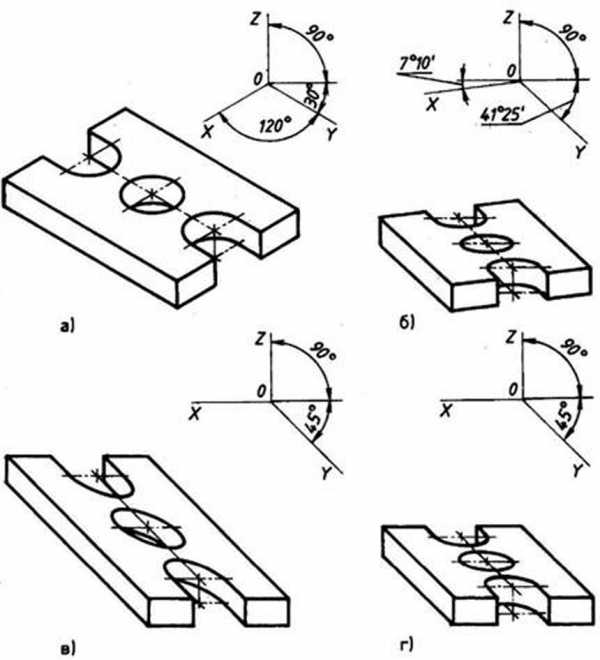
Рис. 107. Аксонометрические проекции, установленные ГОСТ 2.317—69: а — прямоугольная изометрическая проекция; б — прямоугольная диметрическая проекция; в — косоугольная фронтальная изометрическая проекция; г — косоугольная фронтальная диметрическая проекция

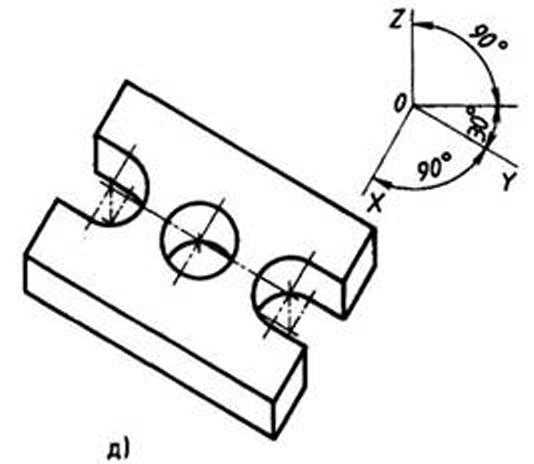
Рис. 107. Продолжение: д — косоугольная горизонтальная изометрическая проекция

При этом проецирующие лучи перпендикулярны аксонометрической плоскости проекций, а координатные оси одинаково наклонены к аксонометрической плоскости проекций (cм. рис. 106). Если сравнить линейные размеры предмета и соответствующие им размеры аксонометрического изображения, то можно увидеть, что на изображении эти размеры меньше, чем действительные. Величины, показывающие отношение размеров проекций отрезков прямых к действительным их размерам, называют коэффициентами искажения. Коэффициенты искажения (К) по осям изометрической проекции одинаковы и равны 0,82, однако для удобства построения используют так называемые практические коэффициенты искажения, которые равны единице (рис. 108).

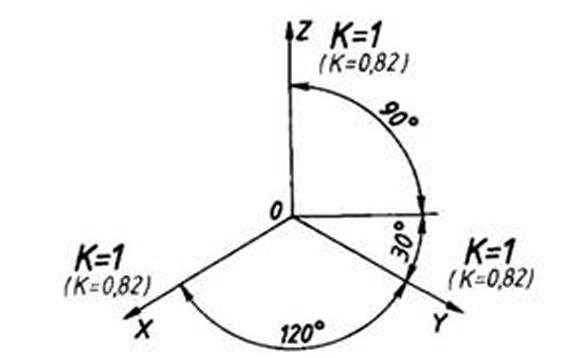
Рис. 108. Положение осей и коэффициенты искажения изометрической проекции

Существуют изометрические, диметрические и триметрические проекции. К изометрическим проекциям относятся такие проекции, которые имеют одинаковые коэффициенты искажения по всем трем осям. Диметрическими проекциями называются такие проекции, у которых два коэффициента искажения по осям одинаковые, а величина третьего отличается от них. К триметрическим проекциям относятся проекции, у которых все коэффициенты искажения различны.

cherch.ru

Прямоугольная диметрическая проекция — КиберПедия

В прямоугольной диметрической проекции аксонометрические оси Ooxo и Oozo составляют между собой угол 97о10’. Ось Ooyo является биссектрисой оставшегося угла, составляя с двумя другими осями равные углы 131о25’ (рис. 11). При построении этой проекции принимают, что

Kx = Kz и Ky = 0,5Kx.

Тогда по основной теореме аксонометрии получаем из формулы

K2x + K2y + K2z = 2, что 2K2x + (0,5Kx)2 = 2,

тогда K2x = 8/9; Kx = 0,94.

Приведенные коэффициенты искажения будут равны:

Kx = Kz = 1; Ky = 0,5,

что соответствует увеличению изображения в 1,06 раза (1/0,94 = 1,06).

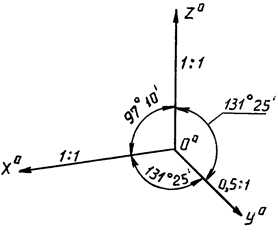
Прямоугольная диметрия рекомендуется к применению в случае, когда наибольшее число характерных особенностей сосредоточено на одной стороне предмета. Наиболее отличающаяся особенностями сторона предмета располагается параллельно плоскости XoOoZo.

Косоугольная фронтальная диметрическая проекция

Аксонометрическая плоскость a располагается параллельно фронтальной плоскости проекций V (рис. 12). Поэтому аксонометрические оси Ooxo и Oozo параллельны декартовым осям Ox и Oz. Соответственно, коэффициенты искажения Kx = Kz. Значение Ky принимается равным 0,5. Расположение аксонометрических осей показано на рисунке .

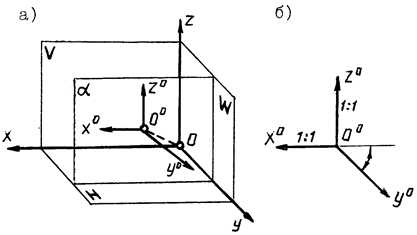
Косоугольная фронтальная диметрия удобна в тех случаях, когда изображаемая геометрическая фигура содержит большое число окружностей (или других кривых, состоящих из дуг окружностей), лежащих на взаимно параллельных плоскостях. При расположении этих плоскостей параллельно аксонометрической плоскости, все окружности будут проецироваться на ней также в виде окружностей, что упрощает построение.

КОМПЛЕКСНЫЙ ЧЕРТЕЖ ТОЧКИ И ПРЯМОЙ

План:

3.1. Комплексный чертеж точки

3.2. Проекции прямых общего положения

3.3. Проекции прямых уровня

Горизонталь - прямая равных высот

Фронталь - прямая равных глубин

Профильная прямая - прямая равных широт

3.4. Проекции проецирующих прямых

Горизонтально-проецирующая прямая

Фронтально-проецирующая прямая

Профильно-проецирующая прямая

3.5. Определение натуральной величины отрезка прямой общего положения

3.6. Деление отрезка прямой в данном отношениè

Комплексный чертеж точки

Внутри трехгранного угла, образованного горизонтальной (H), фронтальной (V) и профильной (W) плоскостями проекций, расположим какую-либо точку А (рис. 13).

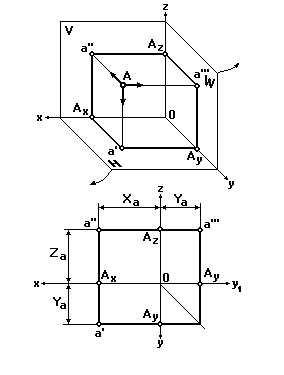
Направим проецирующий луч перпендикулярно плоскости V. Точка пересечения этого луча с плоскостью V будет фронтальной проекцией a'' точки A. Спроецируем точку А на плоскость H и получим ее горизонтальную проекцию a'. Проецируя точку А на плоскость W, получим ее профильную проекцию a'''.

Для получения чертежа необходимо все три плоскости V, H и W вместе с построенными на них проекциями совместить в одну плоскость, т.е. развернуть их.

При этом плоскость H поворачивается вокруг оси x на 90 градусов книзу, плоскость W — вокруг оси z на 90 градусов вправо, а плоскость V остается неподвижной (при этом ось y как бы раздваивается).

В результате совмещения получают чертеж точки в трех проекциях. Очертания плоскостей H, V и W на чертеже не показывают.

Линию, связывающую горизонтальную и профильную проекции точки А, представляют двумя отрезками ломаной линии. Вершина ее лежит на биссектрисе угла, образованного осями y и y1. Эту биссектрису называют постоянной линией чертежа.

Прямые линии, соединяющие проекции точки и перпендикулярные осям проекций, называют линиями проекционной связи (рис. ).

Координатный отрезок, равный превышению точки А над плоскостью H, называют высотой Za (аппликатой) точки А. Координатный отрезок, равный расстоянию от точки А до плоскости V, называют глубиной Ya (ординатой) точки А. Координатный отрезок, равный расстоянию от точки А до плоскости W, называют широтой Xa (абсциссой) точки А.

Горизонтальная проекция точки А определяется на эпюре ее координатами Xa и Ya, а фронтальная — координатами Xa и Za (рис. 13).

cyberpedia.su