5.3.4.Построение развертки усеченного конуса. Чертеж развертка усеченного конуса
Построение разверток - Медницко-жестяницкие работы
Категория:
Медницко-жестяницкие работы
Построение развертокЧтобы изготовить пустотелые изделия различной формы, нужно разметить на листе развертку этого изделия. Наиболее часто составляющие части изделия имеют формы цилиндра и конуса, поэтому рассмотрим построение разверток этих фигур.
Развертка прямого цилиндра представляет собой прямоугольник (рис. 1, а), ширина которого равна высоте цилиндра Н, а длина — длине окружности цилиндра. Для определения этой длины диаметр цилиндра D умножают на число 3,14, обозначаемое в формулах греческой буквой п.
Длина окружности цилиндра определится по формуле L = nD = 3.14D.
Например, если цилиндр имеет диаметр 100 мм, то длина развертки L = 3,14 • 100 = 314 мм. При этом расчете
he учитывают длину материала, идущего на соединительный шов. Полная длина развертки равна длине окружности плюс припуск на шов.
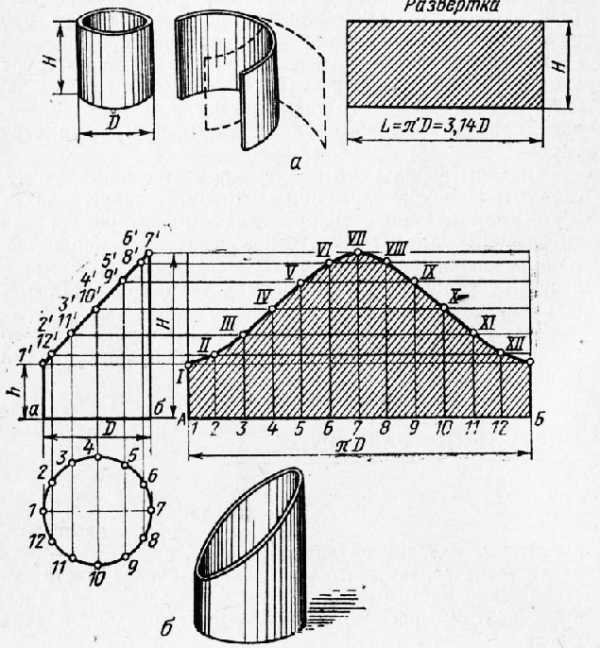
Рис. 1. Построение развертки цилиндра; а — прямого: о — усеченного
Развертка усеченного цилиндра представлена на рисунке 5 б. В натуральную величину вычерчены две проекции усеченного цилиндра: вид сбоку и вид сверху (план). Окружность круга (основания цилиндра) делят на несколько равных частей, проще всего на 12; в результате получают точки 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12. Эти точки соединяют линиями, перпендикулярными диаметру 1—7,
с наклонной линией верхней проекции 1‘—7’. При пересечении получают точки Г; 2’, 12’; 3’, 11’; 4’, 10’; 5’, 9’; 6’, 8’ и 7’. Вправо от верхней проекции проводят линию АБ, которая является продолжением линии аб (основания верхней проекции) и по длине равняется длине окружности основания цилиндра (L = 3,14D). Линию АБ делят на 12 равных частей. Из каждой точки на линии АБ восстанавливают перпендикуляры, а из каждой точки на наклонной Г—V проводят линии, параллельные прямой АБ, до пересечения с этими перпендикулярами. Пересечение линии, проведенной из точки 1’, с перпендикуляром, восстановленным из точки 1 на линии АБ, даст точку I развертки; пересечение линии, проведенной из точки 2’, с перпендикуляром, восстановленным из точки 2, даст точку II развертки и т. д. Соединив все полученные точки плавной кривой, получают развертку усеченного цилиндра в натуральную величину. Если изделие соединяется фальцевыми швами, к развертке прибавляют припуск на швы.
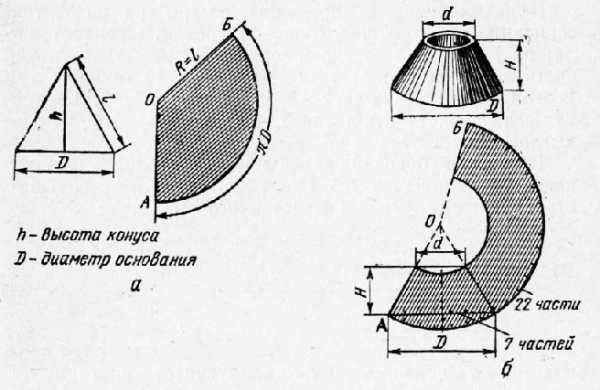
Рис. 2. Построение развертки конуса; а — прямого; б — усеченного
Развертка конуса приведена на рисунке 2а. Для ее построения вычерчивают в натуральную величину боковую проекцию конуса, которая представляет собой треугольник. Высота треугольника равна высоте конуса (h), а основание — диаметру окружности, лежащей в основании конуса (D). На боковой проекции конуса измеряют циркулем сторону треугольника, обозначенную на рисунке буквой, и, не изменяя развода циркуля, проводят рядом с проекцией часть окружности радиусом, равным. От точки А, лежащей на дуге этой окружности, откладывают расстояние, равное L = 3,14D. Для этого берут тонкую проволоку длиной L = 3,14D и от точки А откладывают ее по дуге. Там, где проволока кончится, отмечают точку Б и соединяют точки А и Б с центром О. Полученная фигура АОБ — развертка боковой поверхности конуса. При соединении конуса фальцевым швом прибавляют припуск на шов.
Для ускорения и упрощения построения развертки основание треугольника (боковой проекции конуса) делят на 7 частей, а затем, отмерив циркулем одну такую часть, откладывают от точки А по дуге 22 такие части. В этом случае длина дуги АБ будет равняться 3.14D, так как если представить число 3,14 простой дробью, то оно выглядит как 22/7.
Развертка боковой поверхности усеченного конуса показана на рисунке 2. Построение ее аналогично построению развертки для неусеченного конуса.
Читать далее:
Резка металлов
Статьи по теме:
pereosnastka.ru
5.3.4. Построение развертки усеченного конуса
ем перпендикуляры к каждому отрезку, на них откладываем действительные величины образующих цилиндра, взятые с фронтальной проекции. Соединив полученные точки между собой, получаем кривую.
Для получения полной развертки к развертке боковой поверхности добавляем окружность (основание) и натуральную величину сечения (эллипс), построенный по его большой и малой оси или по точкам.
Вчастном случае развертка конуса представляет собой плоскую фигуру, состоящую из кругового сектора и круга (основания конуса).
Вобщем случае развертывание поверхности производится по принципу развертывания многогранной пирамиды (т. е. способом треугольников), вписанной в коническую поверхность. Чем большее число граней пирамиды, вписанной в коническую поверхность, тем меньше будет разница между действительной и приближенной развертками конической поверхности.
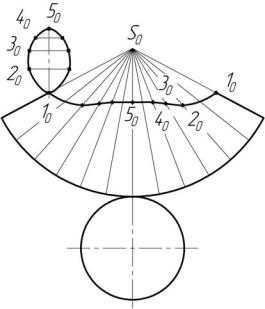
Построение развертки конуса начинается с нанесения из точки S0 дуги окружности радиусом, равным длине образующей конуса. На этой дуге откладывают 12 частей окружности основания конуса и полученные точки соединяют с вершиной. Пример изображения полной развертки усеченного конуса представлен на рис. 5.7.
Рис. 5.7
Лекция 6 (начало)
ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ. СПОСОБЫ ПОСТРОЕНИЯ ВЗАИМНОГО ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ.
СПОСОБ ВСПОМОГАТЕЛЬНЫХ СЕКУЩИХ ПЛОСКОСТЕЙ И ЧАСТНЫЕ СЛУЧАИ
6.1. Взаимное пересечение поверхностей
Пересекаясь между собой, поверхности тел образуют различные ломаные или кривые линии, которые называют линиями взаимного пересечения.
Для построения линий пересечения двух поверхностей нужно найти такие точки, которые одновременно принадлежат двум заданным поверхностям.
Когда одна из поверхностей полностью пронизывает другую, получаются 2 отдельные линии пересечения, называемые ветвями. В случае получения врезки, когда одна поверхность частично входит в другую, линия пересечения поверхностей будет одна.
6.2. Пересечение гранных поверхностей
Линия пересечения двух многогранников представляет собой замкнутую пространственную ломаную линию. Ее звенья являются линиями пересечения граней одного многогранника с гранями другого, а вершины – точки пересечения ребер одного многогранника с гранями другого. Таким образом чтобы построить линию пересечения двух многогранников, нужно решить задачу либо на пересечение двух плоскостей (способ граней), либо на пересечение прямой с плоскостью (способ ребер). На практике обычно используются оба способа в комбинации.
Пересечение пирамиды с призмой. Рассмотрим случай пересече-
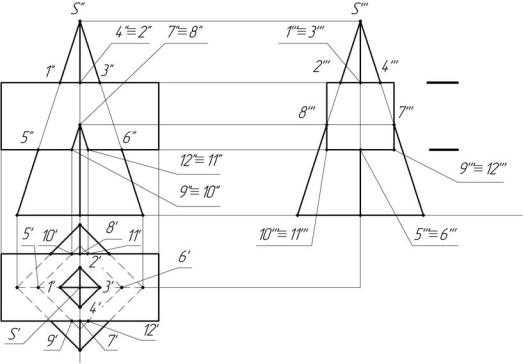
ния пирамиды с призмой, боковая поверхность которой проецируется на π3 на очерковые основания (четырехугольник). Построение начинаем с профильной проекции. При нанесении точек воспользуемся способом ребер, т. е. когда ребра вертикальной пирамиды пересекают грани горизонтальной призмы (рис. 6.1).
α'''
β'''
Рис. 6.1
Анализ условия задачи показывает, что линия пересечения пирамиды и призмы распадается на 2 ветви, одна из ветвей – плоский многоугольник, точки 1,2,3,4 (точки пересечения ребер пирамиды с гранью призмы). Горизонтальные, фронтальные и профильные их проекции находятся на проекциях соответствующих ребер и определяются по линиям связи. Аналогично могут быть найдены точки5,6,7 и8, принадлежащие другой ветви. Точки9,10,11,12 определяются из условия, что верхняя и нижняя грани призмы параллельны между собой, т. е.1' 2' параллельна 5' 10' и т. д.
Можно воспользоваться способом вспомогательных секущих плоскостей. Вспомогательная плоскость пересекает обе поверхности по ломаным линиям. Взаимное пересечение этих линий и дает нам точки, принадлежащие искомой линии пересечения. В качестве вспомогательных плоскостей выбираем α''' и β'''. С помощью плоскости α'''
находим проекции точек 1',2',3',4', а плоскости β''' – точки 5', 6',9', 10',11',12'. Точки7 и8 определяем как в предыдущем способе.
6.3.Пересечение гранных поверхностей
споверхностями вращения
Большинство технических деталей и предметов состоит из сочетания различных геометрических тел. Пересекаясь между собой, по-
верхности этих тел образуют различные прямые или кривые линии, которые называются линиями взаимного пересечения.
Для построения линии пересечения двух поверхностей нужно найти такие точки, которые одновременно принадлежали бы двум поверхностям.
При пересечении многогранника с поверхностью вращения образуется пространственная кривая линия пересечения.
Если происходит полное пересечение (проницание), то образуются две замкнутые кривые линии, а если неполное пересечение – то одна замкнутая пространственная линия пересечения.
Для построения линии взаимного пересечения многогранника с поверхностью вращения используется способ вспомогательных секущих плоскостей. Вспомогательная плоскость пересекает обе поверхности по кривой и по ломаной линиям. Взаимное пересечение этих линий и дает нам точки, принадлежащие искомой линии пересечения.
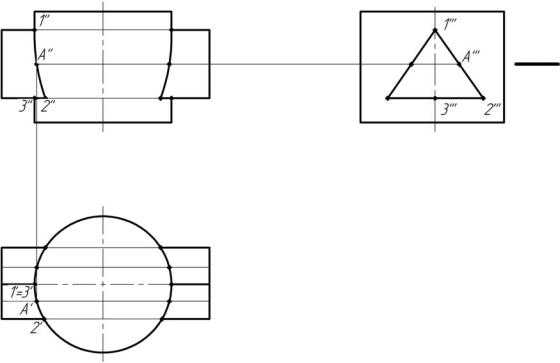
Пусть требуется построить проекции линии пересечения поверхностей цилиндра и треугольной призмы. Как видно из рис. 6.2, в пересечении участвуют все три грани призмы. Две из них направлены под некоторым углом к оси вращения цилиндра, следовательно, пересекают поверхность цилиндра по эллипсам, одна грань перпендикулярна к оси цилиндра, т. е. пересекает его по окружности.
α'''
Рис. 6.2
План решения:
1)находим точки пересечения ребер с поверхностью цилиндра;
2)находим линии пересечения граней с поверхностью цилиндра. Как видно из рис. 6.2, боковая поверхность цилиндра – горизон-
тально-проецирующая,т. е. перпендикулярна горизонтальной плоскости проекций. Боковая поверхность призмы –профильно-проецирую-щая, т. е. каждая ее грань перпендикулярна к профильной плоскости проекций. Следовательно, горизонтальная проекция линии пересечения тел совпадает с горизонтальной проекцией цилиндра, а профильная – с профильной проекцией призмы. Таким образом, на чертеже нужно построить лишь фронтальную проекцию линии пересечения.
Построение начинаем с нанесения характерных точек, т. е. точек, которые можно найти без дополнительных построений. Такими являются точки 1, 2 и 3. Они находятся на пересечении очерковых образующих фронтальных проекций цилиндра с фронтальной проекцией соответствующего ребра призмы с помощью линий связи.
Таким образом, точки пересечения ребер призмы с поверхностью цилиндра построены.
Для того чтобы найти промежуточные точки (всего таких точек четыре, но обозначим одну из них А) линий пересечения цилиндра с гранями призмы, пересекаем обе поверхностикакой-либопроецирующей плоскостью или плоскостью уровня. Возьмем, например, горизонтальную плоскость α. Плоскость α пересекает грани призмы по двум прямым, а цилиндр – по окружности. Эти линии пересекаются в точкеA' (одну точку подписали, а остальные нет), которая принадлежит одновременно и поверхности цилиндра (лежит на окружности, которая принадлежит цилиндру) и поверхности призмы (лежит на прямых линиях, которые принадлежат граням призмы).
Прямые, по которым пересекаются грани призмы с плоскостью α, найдены сначала на профильной проекции многогранника (там они спроецировались в точку A''' и симметричную точку), а затем с помощью линий связи построены на горизонтальной проекции призмы. ТочкаA и симметричные точки получены на пересечении горизонтальной проекции линий пересечения (плоскости α с призмой) с окружностью и при помощи линий связи найдены на фронтальной проекции.
42
studfiles.net
Развертки тел вращения - Mnogogranniki.ru
Что будет, если плоскую геометрическую фигуру, например прямоугольник, начать быстро вращать относительно одной из его сторон?
Одним лишь вращением мы можем создать новое геометрическое тело в пространстве.
Боковые поверхности цилиндра образуются за счет сторон вращающегося прямоугольника.
Официальное определение для таких геометрических тел, звучит следующим образом:Тела вращения — объёмные тела, возникающие при вращении плоской геометрической фигуры, ограниченной кривой, вокруг оси, лежащей в той же плоскости.
И здесь важно то, что плоская геометрическая фигура может быть совершенно произвольной формы.
Например, кривая, которая при вращении будет образовывать вазу или лампочку. Такие инструменты создания тел вращения очень популярны у тех, кто работает в программах 3D-проектирования.
Но с математической точки зрения, для нас, прежде всего, интересны следующие геометрические тела вращения:
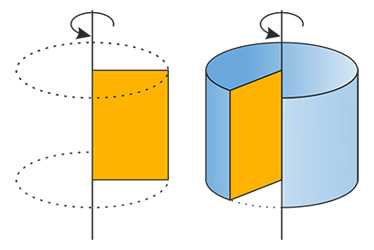
Цилиндр - образован прямоугольником, вращающимся вокруг одной из сторон.
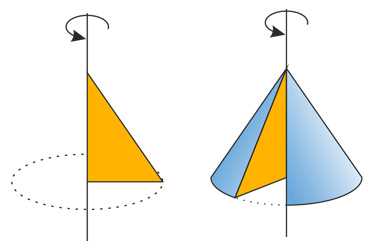
Конус - образован прямоугольным треугольником, вращающимся вокруг одного из катетов.
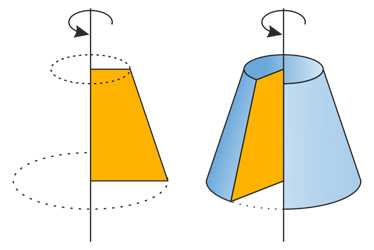
Усечённый конус - часть конуса, расположенная между его основанием и секущей плоскостью, параллельной основанию.
Образуется при вращении прямоугольной трапеции вокруг ее боковой стороны, перпендикулярной основаниям трапеции.
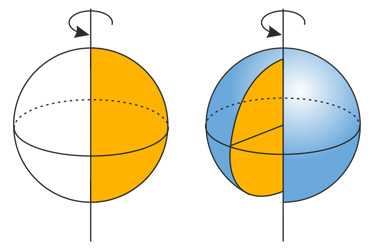
Шар - образован полукругом, вращающимся вокруг диаметра разреза.
При вращении контуров фигур возникает поверхность вращения (например, сфера, образованная окружностью), в то время как при вращении заполненных контуров возникают тела (как шар, образованный кругом).
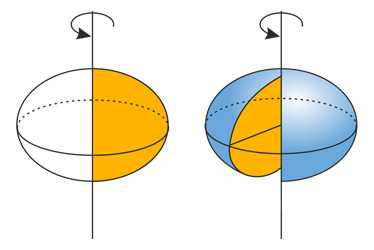
Эллипсоид — поверхность в трёхмерном пространстве, полученная деформацией сферы вдоль трёх взаимно перпендикулярных осей.
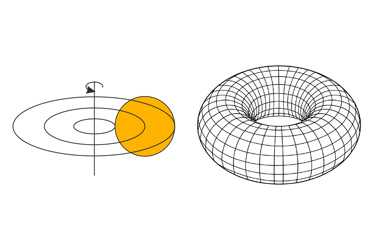
Тор - образован окружностью, вращающейся вокруг прямой, не пересекающей его.
В обычном понимании тор - это "бублик".
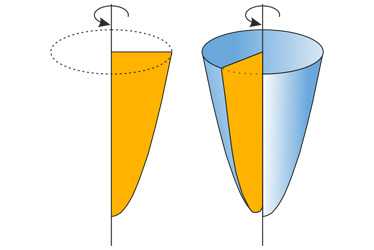
Параболоид - это поверхность, которая образуется в результате вращения вокруг оси кривой образованной графиком параболы. Отсюда и название параб-о-лоид.
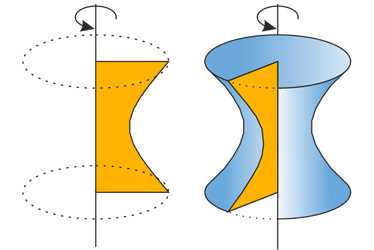
Гиперболоид - это поверхность, которая образуется в результате вращения вокруг оси кривой образованной графиком гиперболы. Соответственно название гиперб-о-лоид.
Как сделать цилиндр из бумаги?
Предлагаем вам построить модель цилиндра, со следующими характеристиками: высота 150 мм, диаметр основания 65 мм.
Скачать развертку цилиндраУсечённый цилиндр, геометрическое тело, отсекаемое от цилиндра плоскостью, непараллельной основанию.
Предлагаем вам построить модель усеченного цилиндра, со следующими характеристиками: высота 165 мм, диаметр основания 65 мм, угол наклона секущей плоскости 45°.
Скачать развертку усечённого цилиндраСхема сборки усеченного цилиндра:
1. Соедините развёртку, так, чтобы получилась трубочка.
2. Чтобы избежать сложностей и сдвигов при приклеивании оснований, мы рекомендуем сначала приклеить вспомогательные элементы. Это позволит безпрепятственно придерживать их при склеивании и создаст правильную форму геометрической конструкции.
3. Аналогичную процедуру проделываем для нижнего основания.
4. Приклеиваем основания.
Пример усечённого цилиндра из архитектуры:В 1989 году в г. Копенгаген (Дания) построили планетарий в форме усеченного цилиндра.
Как сделать конус из бумаги?
Предлагаем вам построить модель усеченного конуса со следующими характеристиками: высота 185 мм, диаметр основания 90 мм.Скачать развертку конуса
Какие могут быть сечения у конуса?
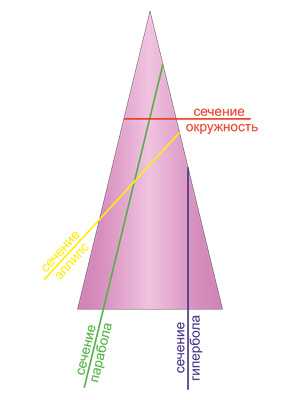
В зависимости от угла наклона секущей плоскости к основанию конуса могут быть образованы четыре варианта сечений: круг, эллипс, парабола, гипербола.
Пример из архитектуры: основание Останкинской телебашни в Москве имеет форму усеченного конуса:
Схема сборки эллиптического конуса:
1. Соедините развёртку, так, чтобы получилась трубочка.
2. Чтобы избежать сложностей и сдвигов при приклеивании
оснований, мы рекомендуем сначала приклеить вспомогательные
элементы. Это позволит безпрепятственно придерживать их
при склеивании и создаст правильную форму геометрической конструкции.
3. Аналогичную процедуру проделываем для нижнего основания.
4. Приклеиваем основания.
Обратите внимание! Других тел вращения построить из бумаги нельзя. Только: цилиндр и конус, включая всевозможные сечения.
Казалось бы, о чем нам еще говорить здесь? Нельзя, значит нельзя. Но есть маленькое «но». Из бумаги можно построить тела приближенные к таким телам вращения как шар, эллипсоид, тор, параболоид и гиперболоид.
То есть, чем больше лепестков будет содержать развертка, тем больше модель будет приближаться к округлой форме.
Как сделать параболоид из бумаги?
Схема сборки параболоида:
1. Склеиваем верхнюю часть развёртки.
2. Соединяем вместе. Образуется куполообразная часть.
3. Чтобы избежать сложностей и сдвигов при приклеивании основания,
мы рекомендуем сначала приклеить вспомогательные элементы.
Это позволит безпрепятственно придерживать их при склеивании и
создаст правильную форму геометрической конструкции.
4. Приклеиваем основание.
Пример из архитектуры.
Здания точно повторяющего формулу параболы нам найти не удалось. Но, тем не менее, в Лондоне (Великобритания) есть небоскрёб с очень необычной формой.Небоскреб Мэри-Экс, именуемый местными жителями «огурец» (англ. The Gherkin), не имеет углов, что не позволяет ветровым потокам стекать вниз и обеспечивает естественную вентиляцию. Высота 41 этажного здания 180 метров. Диаметр здания у основания составляет 49 метров, затем здание плавно расширяется, достигая максимального диаметра в 57 метров на уровне 17 этажа. Далее конструкция сужается, достигая минимального диаметра в 25 метров.
Как сделать гиперболоид из бумаги?
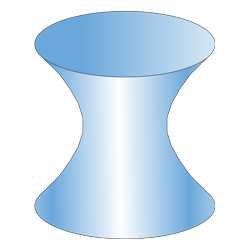
Предлагаем вам построить модель гиперболоида, со следующими характеристиками: высота 110 мм, диаметр основания 70 мм.
Схема сборки гиперболоида:
1. Соединяем две "самые маленькие" полоски через центр.
2. Должно получиться так, как показано на рисунке.
3. Приклеиваем еще две полоски, те, что средние по величине.
4.
5. Приклеиваем самые большие полоски.
6.
7. Соединяем развертку вместе.
8. Чтобы избежать сложностей и сдвигов
при приклеивании оснований,
9. Приклеиваем основания.
Пример гиперболоида из архитектуры.Зданий имеющих формулу гиперболоида достаточно много:Самые первые конструкции были созданы под руководством русского инженера Шухова В.Г. - знаменитая шуховская башня в Москве, год постройки 1922.
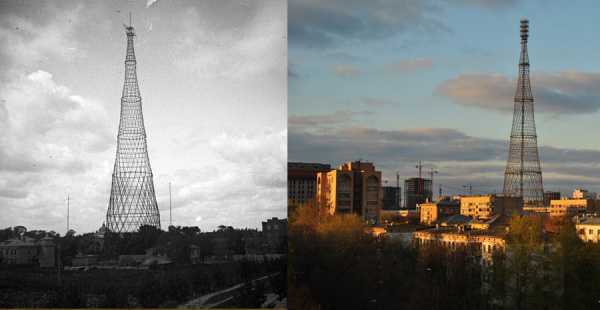Из современных построек отметим башню в г.Гуанчжоу (Китай) высота 600 метров, год посторойки 2010.Кроме того, нам показалась весьма красивой Башня Торнадо в г.Доха (Катар). 195-ти метровая конструкция, возведенная в 2008 имеет свой непередаваемый стиль.
Для сопоставимости размеров получающихся моделей тел вращения мы постарались собрать их на одной поверхности вместе с призмами из выпуска «Волшебные грани № 16».
Получился целый математический город из бумаги, умещающийся на столе!
mnogogranniki.ru
Построение развёртки конуса, усечённого конуса
Цель: научиться выполнять построение разверток конуса, усеченного конуса.
Место проведения: учебная аудитория, ОБОУ СПО «Курский электромеханический техникум».
Средства обучения:
— методические рекомендации к практической работе № 51.
Виды самостоятельной работы:
— построение разверток конуса, усеченного конуса по данным размерам;
— изготовление моделей конуса.
Краткая теоретическая справка
Конусом (точнее, круговым конусом) называется тело, которое состоит из круга — основания конуса, точки, не лежащей в плоскости этого круга,— вершины … конуса и всех отрезков, соединяющих вершину конуса с точками основания.
Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими, конуса.
Поверхность конуса состоит из основания и боковой поверхности.
Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания.
Наглядно прямой круговой конус можно представлять себе как тело, полученное при вращении прямоугольного треугольника вокруг его катета как оси.
Развертка поверхности конуса представляет собой плоскую фигуру, состоящую из сектора — развертки боковой поверхности и круга — основания конуса.
Построение выполняют следующим образом.
Проводят осевую линию и из точки S, взятой на ней, описывают радиусом, равным длине образующей конуса, дугу окружности. На ней откладывают длину окружности основания конуса.
Получить длину дуги, равной длине окружности основания, можно двумя способами:
— разделить окружность основания конуса на несколько частей, а затем отложить их на дуге окружности с радиусом, равным образующей конуса;
— от проведенной осевой линии отложить центральный угол, соответствующий длине окружности основания.
Выразим данный угол через радиус основания r и длину образующей l конуса.
Длина дуги АВА/ равна (длине окружности основания конуса). С другой стороны углу соответствует дуга АВА/ длиной, равной .
Значит, . Откуда .
Точку S соединяют с конечными точками дуги;
К полученной фигуре пристраивают круг. Диаметр этого круга равен диаметру основания конуса.
Практические задания
1. Построить развертку прямого кругового конуса с радиусом основания, равным 2 см, и образующей 5 см.
2. Построить развертку усеченного конуса с радиусами основания 2 и 3см и образующей полного конуса 5 см.
3. По построенным разверткам изготовить модель конуса.
Требования к отчёту:
1. После выполнения работы студент обязан продемонстрировать преподавателю выполненные задания.
2. Предоставить отчёт о выполненной работе, содержащий:
— порядковый номер и наименование практической работы;
— цель практической работы;
— ход выполнения работы;
— ответы на контрольные вопросы.
Контрольные вопросы
1. Что такое конус?
2. Почему конус называют телом вращения?
3. Что такое образующая конуса?
4. Какой конус называют прямым?
5. Что представляет собой развертка конуса?
6. Что такое усеченный конус и как построить его развертку?
Сделайте вывод о том, какие математические навыки были приобретены вами в ходе выполнения данной практической работы.
refac.ru
