Большая Энциклопедия Нефти и Газа. Наклонный цилиндр

Объем цилиндра: формула, калькулятор - 24СМИ

Как отличить человека технической специальности от человека с гуманитарным складом ума? Спросите каждого, что такое цилиндр. Первый скажет, что это геометрическое тело, второй вспомнит мужской головной убор 19 века. Оба будут правы, да и шляпа получила такое название благодаря особенной форме, основой которой являлась та самая фигура из геометрии. Итак, каковы особенности цилиндра и как рассчитать его объем.

Расчет объема цилиндра

Слово «цилиндр» произошло от древнегреческого kylindros, означающего «валик». Математики дают несколько определений цилиндру:

Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее под прямым углом.
Цилиндр — это тело вращения, которое получается при вращении прямоугольника вокруг его стороны.
Цилиндр — геометрическое тело, которое сформировано вращением прямоугольника на оси, совпадающей с одной из его сторон.

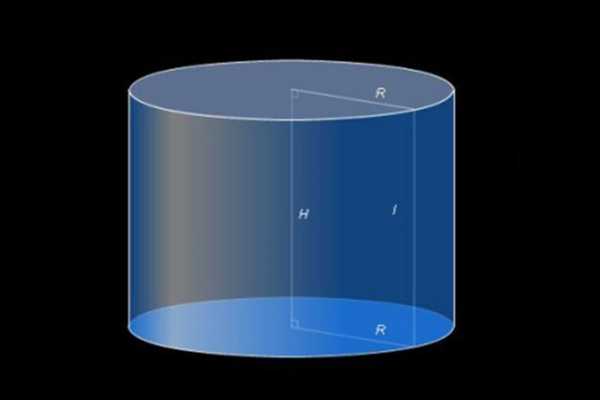Фигура цилиндр

Все эти определения верны. Также стоит отметить основные части цилиндра:

Основания — плоские фигуры, образованные пересечением цилиндрической поверхности с двумя параллельными плоскостями.
Боковая поверхность цилиндра — поверхность между плоскостями оснований.

Если в основании цилиндра лежит круг, то его называют круговым. Существуют и другие виды цилиндров, в зависимости от формы основания — эллиптический, гиперболический, параболический и т.д.

Также все цилиндры делятся на прямые и наклонные. У каждого цилиндра есть образующие — это отрезки, соединяющие соответствующие точки оснований. Если образующие перпендикулярны основаниям, то цилиндр называется прямым, а если образующие расположены под углом — цилиндр наклонный или косой.

Рисунок цилиндра

Есть и другие общие понятия для цилиндров:

Основания цилиндра равны и лежат в параллельных плоскостях. У цилиндра образующие параллельны и равны.
Поверхность цилиндра состоит из оснований и боковой поверхности. Боковая поверхность составлена из образующих.

Радиусом цилиндра называется радиус его основания.
Высотой цилиндра называется расстояние между плоскостями оснований.
Осью цилиндра называется прямая, проходящая через центры оснований.
Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением.
Плоскость, проходящая через образующую прямого цилиндра и перпендикулярная осевому сечению, проведенному через эту образующую, называется касательной плоскостью цилиндра.

Итак, как же вычислить объем цилиндра. Посчитать объем прямого кругового цилиндра можно на калькуляторе. Он равен произведению площади основания на высоту.

V = πR2h,

где V — объем цилиндра, R — радиус основания, h — высота цилиндра, а «пи» — константа, равная 3,14.

Объем цилиндр

Таким же образом вычисляется объем прямого кругового цилиндра через диаметр окружности основания — d.

V = πhd2/4

Если цилиндр прямой, но не круговой, то формула вычисления объема представляет произведение длины образующей – n на площадь сечения цилиндра плоскостью, перпендикулярной образующей — S.

V = n * S

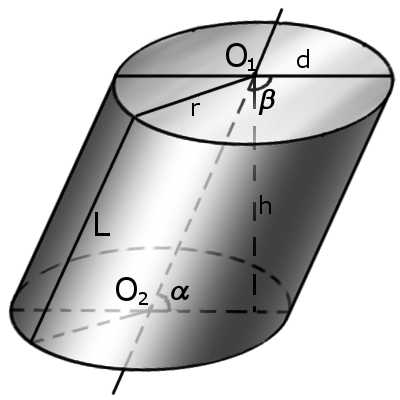Наклонный цилиндр

Если цилиндр наклонный, то в формуле участвует и синус угла наклона (альфа) образующей к основанию. В этом случае объем вычисляется по формуле:

V = S * n * sin α

Исчисляется объем цилиндра в кубических единицах.

Если стоит задача найти объем описанного вокруг сферы цилиндра, то расчеты будут такими:

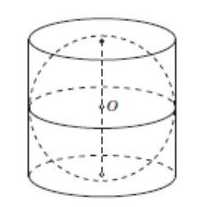Цилиндр и сфера

Радиус цилиндра равен радиусу сферы — R. Высота цилиндра равна диаметру сферы. Диаметр есть удвоенный радиус — 2R. Таким образом объем прямого описанного цилиндра равен произведению площади основания πR2 («пи» умножить на радиус в квадрате) на высоту, т. е. 2R.

V = 2R * πR2

Приведя формулу к должному виду получим:

V = 2πR3

Если цилиндр вписан в прямоугольный параллелепипед, то, зная длину стороны его основания и высоту, можно найти объем.

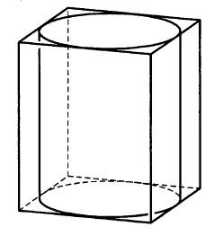Цилиндр, вписанный в параллелепипед

В этом случае радиус основания цилиндра равен половине длины стороны основания параллелепипеда — а. Высота цилиндра и параллелепипеда совпадают, обозначим h. Тогда объем вычисляется по формуле:

V = πh(a/2)2

Где применяется расчет объема цилиндра

Расчет объема цилиндра учащиеся проходят в средней школе. Во взрослой жизни эти знания применяют в своей работе инженеры и конструкторы различных машин и механизмов, потребительских товаров, а также архитекторы.

Из товаров народного потребления форму цилиндра имеют стаканы, кружки, бокалы, кастрюли, термосы и прочая посуда, а также некоторые вазы, банки и упаковки напитков либо средств бытовой химии. Объем таких цилиндрических предметов исчисляется в литрах.

Стаканы имеют цилиндрическую форму

Рассчитывается объем цилиндра при производстве медицинских шприцов. От полученного объема зависит точное количество медикаментов, вводимое пациенту при инъекциях. Лекарства в жидкой форме, суспензии, растворы помещаются в стеклянные или пластиковые бутылочки цилиндрической формы, а на бирке указывается объем средства.

Распространены цилиндры и в технике: такой вид имеют валы и их отдельные составные части, используемые в двигателях внутреннего сгорания. К тому же, расчет объема цилиндра – задача, которую приходится решать конструкторам при проектировании современных бензиновых и дизельных силовых агрегатов, ведь от этого параметра зависят характеристики, в первую очередь, мощность. Двигатели внутреннего сгорания снабжаются поршнями, которые также имеют цилиндрическую форму.

Расчет цилиндрического вала

Архитекторам приходится рассчитывать объем цилиндра при проектировании зданий, снабженных колоннами. Правда, эти архитектурные элементы в классическом варианте (вместе с базой и капителем) встречаются редко, но упрощенные разновидности, состоящие из одного ствола (который и представляет собой цилиндр) используются часто.

Чрезвычайно распространенные детали, которые присутствуют в конструкциях технических устройств — роликовые подшипники. Как нетрудно догадаться по названию, главный компонент — прочные и износостойкие металлические цилиндрические ролики. Благодаря такой геометрии, эти детали обладают большой несущей способностью и способны выдерживать нагрузки. Роликовые подшипники — высокоточные детали, и поэтому при их создании правильный расчет объема цилиндра (ролика) играет немаловажную роль.

24smi.org

Цилиндр, площадь цилиндра

Цилиндр (происходит из греческого языка, от слов "каток", "валик") – это геометрическое тело, которое ограничено снаружи поверхностью, называющейся цилиндрической, и двумя плоскостями. Данные плоскости пересекают поверхность фигуры и являются параллельными друг другу.

Цилиндрическая поверхность – это поверхность, которая получена поступательными движениями прямой линии в пространстве. Эти движения таковы, что выделенная точка этой прямой линии совершает движение вдоль кривой плоского типа. Такая прямая линия называется образующей, а кривая линия – направляющей.

Цилиндр состоит из пары оснований и боковой цилиндрической поверхности. Цилиндры бывают нескольких видов:

1. Круговой, прямой цилиндр. У такого цилиндра основания и направляющая перпендикулярны образующей линии, и имеется ось симметрии.

2. Наклонный цилиндр. У него угол между образующей линией и основанием не является прямым.

3. Цилиндр иной формы. Гиперболический, эллиптический, параболический и другие.

Площадь цилиндра, а также площадь полной поверхности любого цилиндра находится с помощью сложения площадей оснований этой фигуры и площади боковой поверхности.

Формула, по которой вычисляется полная площадь цилиндра для кругового, прямого цилиндра:

Sp = 2п Rh + 2п R2 = 2п R (h+R).

Площадь боковой поверхности ищется чуть сложнее, чем площадь цилиндра целиком, она вычисляется путем умножения длины образующей линии на периметр сечения, образованного плоскостью, которая перпендикулярна образующей линии.

Данная площадь поверхности цилиндра для кругового, прямого цилиндра узнается по развертке этого объекта.

Развертка – это прямоугольник, который имеет высоту h и длину P, которая приравнивается периметру основания.

Отсюда следует, что боковая площадь цилиндра является равной площади развертки и может быть вычислена по данной формуле:

Sb = Ph.

Если взять круговой, прямой цилиндр, то для него:

P = 2п R, а Sb = 2п Rh.

Если цилиндр наклонный, то площадь боковой поверхности должна быть равна произведению длины его образующей линии и периметра сечения, которое перпендикулярно данной образующей линии.

К сожалению, не существует простой формулы для выражения площади боковой поверхности наклонного цилиндра через его высоту и параметры его основания.

Чтобы вычислить площадь сечения цилиндра, необходимо знать несколько фактов. Если сечение своей плоскостью пересекает основания, то такое сечение всегда является прямоугольником. Но эти прямоугольники будут разными, в зависимости от положения сечения. Одна из сторон осевого сечения фигуры, которое перпендикулярно основаниям, равна высоте, а другая - диаметру основания цилиндра. А площадь такого сечения, соответственно, приравнивается произведению одной стороны прямоугольника на другую, перпендикулярную первой, или произведению высоты данной фигуры на диаметр его основания.

Если сечение будет перпендикулярно основаниям фигуры, но не будет проходить через ось вращения, то площадь этого сечения будет равна произведению высоты этого цилиндра и определенной хорды. Чтобы получить хорду, нужно построить окружность у основания цилиндра, провести радиус и отложить на нем расстояние, на котором находится сечение. А от этой точки нужно провести перпендикуляры к радиусу от пересечения с окружностью. Точки пересечения соединяются с центром. А основание треугольника – это искомая хорда, длина которой ищется по теореме Пифагора. Теорема Пифагора звучит так: «Сумма квадратов двух катетов равна гипотенузе, возведенной в квадрат»:

С2 = А2 + В2.

Если сечение не затрагивает основания цилиндра, а сам цилиндр круговой и прямой, то площадь этого сечения находится как площадь окружности.

Площадь окружности равна:

S окр. = 2п R2.

Чтобы найти радиус окружности R, нужно ее длину C разделить на 2п:

R = C \ 2п, где п – число пи, математическая постоянная, вычисленная для работы с данными окружности и равная 3,14.

fb.ru

Цилиндр

Понятие цилиндра

Определение 1

Геометрическая фигура, образованная двумя равными кругами, лежащими в параллельных плоскостях, все точки которых соединены между параллельными прямыми, так что никакая точка не остается несоединенной, называется цилиндром (рис. 1).

Рисунок 1. Цилиндр

Круги при этом называются основаниями цилиндра, а прямые их соединяющие -- образующими. Прямая, которая проходит через центры окружностей оснований называется осью цилиндра, а совокупность всех образующих -- боковой поверхностью цилиндра.

Виды цилиндров

Определение 2

Цилиндр, у которого все образующие перпендикулярны к плоскостям, проходящим через основания, называется прямым. В противном же случае он является наклонным (рис. 2).

Рисунок 2. Прямой и наклонный цилиндры

Площадь поверхности цилиндра

Площадь поверхности цилиндра определяется следующим образом:

Найдем теперь формулы для вычисления площадь боковой поверхности и основания.

Так как в основании лежат круги, то очевидно, что

Теорема 1

Площадь боковой поверхности цилиндра определяется как произведение длины окружности, ограничивающей основание цилиндра на его высоту.

Доказательство.

Для доказательства этой теоремы нам необходимо найти площадь развертки боковой поверхности цилиндра (рис. 3).

Рисунок 3.

Видим, что разверткой боковой поверхности цилиндра является прямоугольник. Высота прямоугольника равняется высоте цилиндра $h$, а длина равняется длине окружности, ограничивающей основание цилиндра, то есть

Теорема доказана.

Объем цилиндра

Теорема 2

Объем цилиндра определяется как произведение площади основания цилиндра на его высоту.

Доказательство.

Рассмотрим цилиндр с радиусом $r$ и высотой $h$. Найдем ее объем $V$. Для этого сначала впишем в нее правильную $n-$угольную призму, в которую впишем еще один цилиндр. Пусть радиус второго цилиндра равняется $r'$, а её объем равен $V'$ (рис. 4).

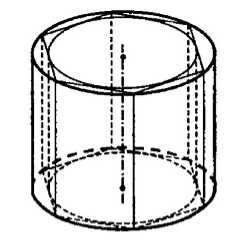
Рисунок 4.

Как мы знаем, объем призмы будет равен $S_{осн.пр.}h$. Следовательно, получим следующую оценку

Тогда из оценки, получим

Теорема доказана.

Пример задачи

Пример 1

Найти площадь полной поверхности цилиндра и его объем, если радиус его основания равняется $7$ см, а высота в два раза больше диаметра основания.

Решение.

Найдем вначале высоту цилиндра. Так как высота в два раза больше диаметра, получим

\[h=2\cdot 2r=4r=28\ см\]

Как мы знаем

\[S_{осн}=\pi r^2=49\pi \]

По теореме 1

\[S_{бок}=2\pi rh=392\pi \]

Тогда

\[S_{полн}=S_{бок}+2S_{осн}=392\pi +98\pi =490\pi \]

По теореме 2

\[V=\pi r^2h=49\pi \cdot 28=1372\pi \]

Ответ: $490\pi ,\ 1372\pi $

spravochnick.ru

Наклон - цилиндр - Большая Энциклопедия Нефти и Газа, статья, страница 1

Наклон - цилиндр

Cтраница 1

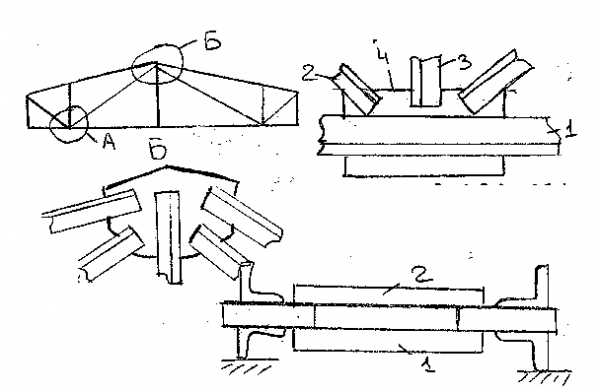
Наклон цилиндра проверяют по отвесу, опущенному по оси втулки ( см. фиг. Для быстрого успокоения колебаний отвеса груз погружают в сосуд, наполненный маслом и установленный на дно корыта фундаментной рамы. Перед опусканием отвеса коленчатый вал должен быть повернут так, чтобы щеки колена расположились горизонтально. Струну отвеса устанавливают по цент: ру верхней части цилиндра так, чтобы груз на 50 - 60 мм не доходил до дна и е касался стенок сосуда. Для ускорения центровки струну крепят при помощи скобочки, передвигаемой по доске. Доска зажимается гайками двух диаметрально противоположных шпилек крышки цилиндра. В ней по центру цилиндра сверлят отверстие диаметром 8 - 10 мм или делают прорезь 10 X 25 мм, на которую накладывают скобку с крючком для креп ления отвеса. Расстояние от струны до стенки цилиндра измеряют при помощи микрометрического штихмаса, а при его отсутствии - простым штихмасом, изготовленным из проволоки диаметром 5 - 7 мм. [1]

Наклон цилиндра вперед не приводит к принципиальным отличиям по сравнению с вертикальным цилиндром. [2]

С увеличением угла наклона цилиндра ( рис. 8.2 в) интенсивность восходящего потока уменьшается, и при а 90 ( рис. 8.2 г) отстой характеризуется спокойным накоплением воды у верхней стенки цилиндра. [3]

С увеличением угла наклона цилиндра ( рис. 75 е) интенсивность движения потока уменьшается, а при горизонтально установленном цилиндре ( рис. 75 г) отстой характеризуется спокойным накоплением воды у верхней стенки цилиндра. [5]

Разность замеров - это величина наклона цилиндра по оси. По ходу наклон оси цилиндра определяют уровнем. [7]

При определении положения оси цилиндра вертикальных компрессоров и небольших двигателей замеряют наклон цилиндра по оси рейсмусом ( см. рис. 68, б) при положении мотылевой шейки кривошипа в в. Разность замеров определяет величину наклона цилиндра по оси. По ходу наклон оси цилиндра определяют уровнем. [8]

В этой печи скорость движения шихты и расплава может регулироваться за счет изменения угла наклона цилиндров и числа оборотов их вращения. [9]

Аль-Араби и Хамиз [9] получили экспериментальные данные по теплоотдаче от изотермических наклонных цилиндров в воздухе для различных углов наклона цилиндра как при ламинарном, так и при турбулентном режиме течения. Аль-Араби и Сэлман [10] также измерили коэффициенты теплоотдачи от равномерно нагреваемого наклонного цилиндра при условии постоянной плотности теплового потока на поверхности. При ламинарном режиме течения указаны корреляционные формулы для местного и среднего коэффициентов теплоотдачи. [10]

Аль-Араби и Хамиз [9] получили экспериментальные данные по теплоотдаче от изотермических наклонных цилиндров в воздухе для различных углов наклона цилиндра как при ламинарном, так и при турбулентном режиме течения. Аль - Араби и Сэлман [10] также измерили коэффициенты теплоотдачи от равномерно нагреваемого наклонного цилиндра при условии постоянной плотности теплового потока на поверхности. При ламинарном режиме течения указаны корреляционные формулы для местного и среднего коэффициентов теплоотдачи. [11]

При монтаже пневмоцилиндров, монтируемых на цапфах, цилиндр должен беспрепятственно качаться на цапфах в пределах заданного угла поворота, что проверяется путем наклона цилиндра на заданный угол. [12]

Боковые стенки станины имеют фиксатор в виде цилиндрического стержня 14 -, удерживающего цилиндр в положении под углом 75, и два съемных стопора для углов наклона цилиндра приблизительно на 23 и 11, что позволяет варьировать время качения в отношении 4: 2: 1 для жидкости данной вязкости и для трубки и шарика данных размеров. [13]

Если наклонный цилиндр условно разделить на элементы ( /, т, п, о), то в каждом из них вода поднимается вверх, как это показано в положении а. При определенном угле наклона цилиндра скорость движения воды вдоль его верхней стенки максимальна. [14]

Страницы: 1 2

www.ngpedia.ru

Цилиндр, конус, шар, развёртка цилиндра и конуса

Цилиндр, конус и шар относятся к объемным (трехмерным) геометрическим фигурам вращения.

Объемные фигуры вращения (еще говорят — «тела», подразумевая объемность фигуры), как правило, образованы вращением плоской фигуры вокруг какой-то линии (прямой).

Так, цилиндр — это фигура, полученная от вращения прямоугольника вокруг одной из его сторон как оси; конус — вращением прямоугольного треугольника вокруг его катета как оси, шар — вращением полукруга вокруг его диаметра как оси.

Объемные фигуры бывают прямые (прямой цилиндр, прямой конус) и наклонные (наклонный цилиндр, наклонный конус), что зависит от вида той плоской геометрической фигуры, которая их образует.

В курсе математики для б класса рассматриваются только прямые цилиндры и конусы

Определение. Цилиндр — это тело (объемная геометрическая фигура), полученное вращением прямоугольника вокруг одной из его сторон как оси.

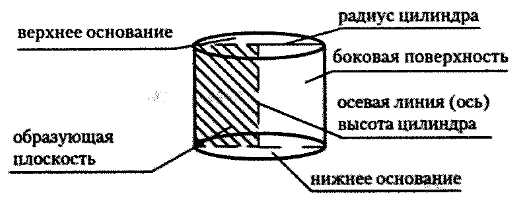
Определение. Конус (прямой) — это тело (объемная геометрическая фигура), полученное вращением прямоугольного треугольника вокруг его катета как оси.

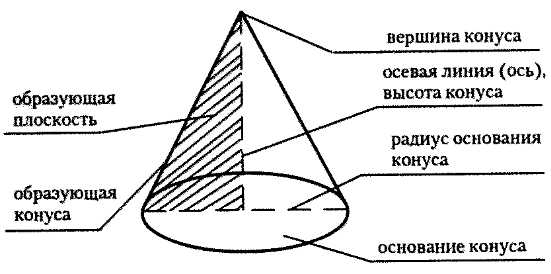
Определение. Шар — это тело (объемная геометрическая фигура), полученное вращением полукруга вокруг его диаметра как оси.

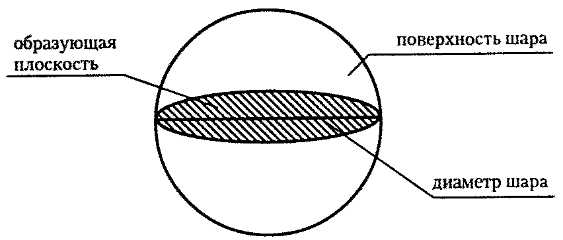
Развертки цилиндра и конуса

Разверткой геометрической фигуры называется изображение плоскости, ограничивающей фигуру, в одной плоскости листа по размерам фигуры.

Развертка цилиндра приведена схематически.

Развертка конуса приведена схематически.

Площади боковой поверхности цилиндра и конуса

Правило. Площадь боковой поверхности цилиндра равна произведению длины окружности основания и высоты цилиндра.

где C — длина окружности, H — высота цилиндра, R — радиус окружности основания.

Правило. Площадь боковой поверхности конуса равна произведению половины длины окружности основания и образующей конуса.

где C — длина окружности основания, l — длина образующей конуса, R — радиус основания.

Площадь поверхности шара

Правило. Площадь поверхности шара равна учетверенной площади большого круга шара.

где R — радиус шара.

Объемы цилиндра, конуса и шара

Правило. Объем цилиндра равен произведению площади основания н высоты.

где R — радиус основания, H — высота цилиндра.

Правило. Объем конуса равен одной трети произведения площади основания и высоты конуса.

где R — радиус основания, H — высота конуса.

Правило. Объем шара равен четырем третямпроизведения числа Пи на куб радиуса.

где R — радиус шара.

shkolo.ru

Наклонный цилиндр развертка. | МеханикИнфо

Развертка наклонного усеченного цилиндра. Наклонный цилиндр развертка. 4.60/5 (92.00%) проголосовало 5

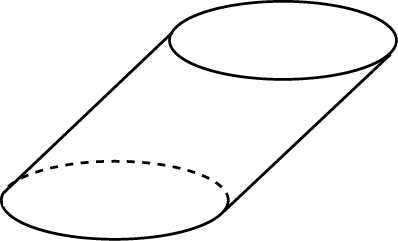
Возьмем вертикальную и горизонтальную проекции наклонного усеченного цилиндра (рис. 1, а), причем нижнее основание цилиндра проектируется на горизонтальную проекцию без искажения, а верхнее основание проектируется также на горизонтальную проекцию в искаженном виде. Действительная форма верхнего основания проектируется на дополнительную плоскость проекции.

Развертку наклонного усеченного цилиндра (рис. 1, б) получают аналогично развертке усеченного цилиндра. Плоскостью, перпендикулярной к образующим, цилиндр делят по линии mn на два усеченных цилиндра.

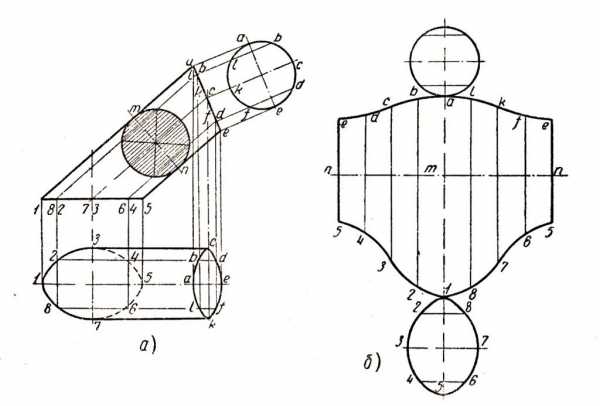
Рис 1. Развертка наклонного усеченного цилиндра:

а — проекция; в — развертка.

На линии mn строится истинное сечение цилиндра, которое будет окружностью. Окружность делится на равное число частей на пример, на восемь частей. Через полученные точки деления окружности проводят образующие цилиндра. Дальнейшее построение истинных очертаний срезанных поверхностей наклонного цилиндра и их проекций видно из рис. 1, б. Каждый полученный цилиндр развертывают в плоскость так, как показано в ст. Развертка усеченного цилиндра, и получают развертку поверхности каждого цилиндра. Сумма обеих разверток с добавлением верхнего и нижнего оснований цилиндра образует полную развертку.

mechanicinfo.ru

Развертка наклонного цилиндра — КиберПедия

Чтобы построить развертку цилиндра, необходимо вписать в него призму с достаточно большим числом граней и развернуть ее. Чем больше граней у вспомогательной призмы, тем точнее развертка.

Примечание. Рекомендуется окружность основания цилиндра делить на 12 равных частей при R>25 мм и на 8 – при R<25 мм (R – радиус основания цилиндра).

Развертывание цилиндрической поверхности общего вида производится по схеме развертывания боковой поверхности наклонной призмы. Отличительной особенностью является то, что полученные точки боковой поверхности, описывающие окружности оснований цилиндра, соединяются не прямыми, а кривыми линиями с помощью лекал.

Основания цилиндра на развертке изображаются окружностями (в натуральную величину каждое), которые касаются в любой точке кривой боковой поверхности, описывающей это основание.

Методика построения линии пересечения поверхностей на развертке наклонного цилиндра аналогична методике, используемой при развертке призмы.

Частные случаи разверток

К частным случаям разверток относятся развертки прямого кругового конуса и прямого кругового цилиндра.

Развертка прямого кругового конуса.Развертка прямого кругового конуса (рис. 119) представляет собой сектор круга, радиус которого равен длине образующей конуса b, а центральный угол а

, (1)

где R – радиус основания конуса.

Нанесение линии на развертку производится по точкам с использованием лекал. Для определения положения любой точки поверхности на развертке, например, точки N, вначале находят положения проекций k1и k2 образующей k, которой принадлежит эта точка. Затем прямую k наносят на развертку при условии, что длина дуги A0K0 равна длине дуги A1K1. Далее, используя теорему Фалеса, определяют истинное положение точки N0: ([K0N0] =m).

Примечание. Развертку прямого конуса можно строить как развертку конической поверхности общего вида, т.е. в конус необходимо вписать правильную многогранную пирамиду.

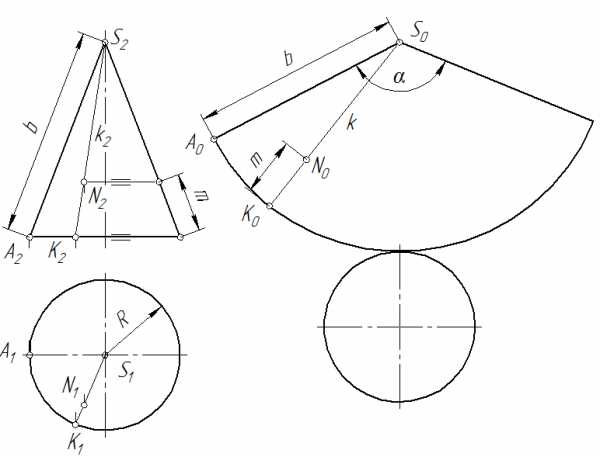
Рис. 119

Методика построения линии пересечения поверхностей на развертке конуса аналогична методике, используемой при развертке пирамиды.

Развертка прямого цилиндра.Развертка боковой поверхности прямого цилиндра представляет собой прямоугольник (рис. 120), одна сторона которого равна образующей l, а другая – длине окружности основания n:

n=2πR, (2)

где R – радиус основания окружности.

Каждое основание цилиндра наносят в виде круга с радиусом R,касающегося в любой точке стороны п прямоугольника, описывающего его.

Нанесение линии пересечения поверхностей на развертку производится по точкам с использованием лекал. Положение любой точки поверхности на развертке, например N, определяется следующим образом. Вначале находят проекции k1 и k2 образующей k, которой принадлежит точка N. Затем определяют положение этой образующей на развертке по условию, что отрезок [B0K0] равен длине дуги B1K1. Так как k2=k, то положение точки N0на развертке определяется как [N0K2]= [N2K2].

Примечание. Развертку прямого цилиндра можно строить как развертку наклонного цилиндра, т.е. в цилиндр необходимо вписать правильную многогранную призму.

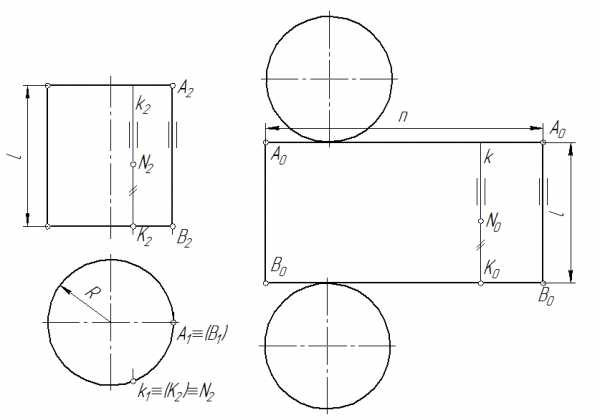
Рис. 120

Развертка сферы

Сферическая поверхность является неразвертываемой. Здесь можно говорить только об условном развертывании. На рис. 121 показан один из приемов построения. Поверхность “разрезают” несколькими плоскостями, проходящими через ось сферы, перпендикулярную π1. Точность развертки зависит от числа плоскостей – чем больше плоскостей, тем точнее развертка. На рис. 104 число таких плоскостей 12 (фронтальные проекции линий пересечения не показаны).

Дуги окружностей на плоскости π1 в лепестках развертки заменяют прямыми, касательными к этим дугам, например, прямая А1В1 заменяет дугу ав.

На плоскости π2дугу 1272делят на равные части: 1222=2232=...=6272 (чем больше частей – тем точнее развертка). Принимая точки 12 22, 32,... за фронтальные проекции отрезков АВ, CD, EF,образующих лепестки развертки, строят их горизонтальные проекции A1B1,C1D1, E1F1,...

На прямой l откладывают отрезок A0B0= A1B1 и через его середину (точка 10) проводят перпендикуляр k. На этом перпендикуляре откладывают отрезки [1020]= 1222, [2030]= 2232, [3040]= 3242, [4050]= 4252, [5262]= 5262и[6272]= 6272и через полученные точки 20, 30, 40, 50,и60проводят отрезки [C0D0]=[C1D1], [E0F0]=[E1F1] и т.д., параллельные прямой A0B0, при этом точки 21≡20,31≡30 и т.д.

По лекало через полученные точки А0, D0, F0,...,70 и В0 С0, E0…, 70 проводят кривые. В результате получается приближенная развертка половины лепестка сферической поверхности. Далее, используя эту часть лепестка, строят недостающую часть развертки.

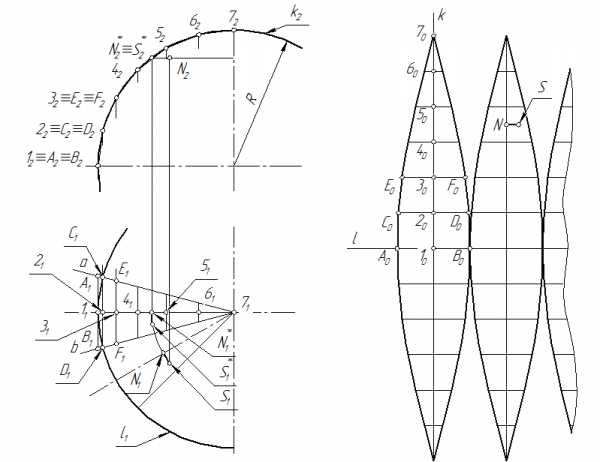
Рис. 121

Примечания.

1. Окружность сферы рекомендуется делить на 12 равных частей (лепестков) при R>25 мм и на 8 – при R<25 мм (R – радиус сферы).

2. Дугу 1272 следует делить не менее чем на 4 равные части (6, 8, 10 или 12 частей).

Построение линии пересечения поверхностей на развертке производится по ее точкам с использованием лекал.

Для нахождения положения точки на развертке, например, S, определяют ее положение относительно экватора ( 12S*2) и центральной линии сегмента [S1N1], в котором она находится. Далее полученные значения этих величин наносят на развертку, т.е. [1N]- 12S2* и [SN]=[S1N1].

16.4. Контрольные вопросы

1. Какую форму имеет развёртка поверхности прямого кругового конуса?

2. Как нанести на развёртку прямого кругового конуса точку, ей принадлежащую?

3. Какую форму имеет развёртка поверхности прямого кругового цилиндра?

4. Как нанести на развёртку прямого кругового цилиндра точку, ей принадлежащую?

5. Каким способом сроят развёртки наклонных цилиндрических поверхностей?

6. Как нанести на развёртку наклонной цилиндрической поверхности точку, ей принадлежащую?

7. Каким способом строят развертку сферы?

8. Как нанести на развёртку сферы точку, ей принадлежащую?

Лекция 17. АКСОНОМЕТРИЯ

17.1. Общие сведения об аксонометрии.

17.2. Прямоугольная изометрическая проекция.

17.3. Прямоугольная диметрическая проекция.

17.4. Построение аксонометрического изображения тел.

17.5. Контрольные вопросы.

cyberpedia.su