Прямоугольная изометрическая проекция. Прямоугольная изометрическая проекция

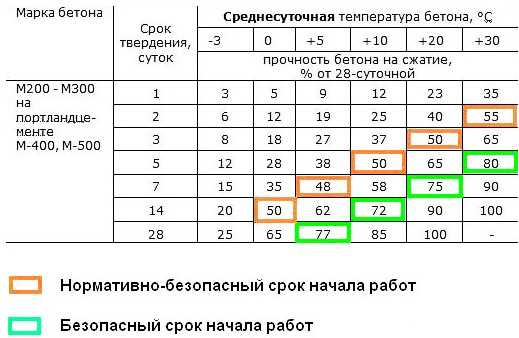
Изометрическая проекция - это... Что такое Изометрическая проекция?

Стол в прямоугольной изометрической проекции

Изометри́ческая прое́кция — это разновидность аксонометрической проекции, при которой в отображении трёхмерного объекта на плоскость коэффициент искажения (отношение длины спроектированного на плоскость отрезка, параллельного координатной оси, к действительной длине отрезка) по всем трём осям один и тот же. Слово «изометрическая» в названии проекции пришло из греческого языка и означает «равный размер», отражая тот факт, что в этой проекции масштабы по всем осям равны. В других видах проекций это не так.

Изометрическая проекция используется в машиностроительном черчении и САПР для построения наглядного изображения детали на чертеже, а также в компьютерных играх для трёхмерных объектов и панорам.

Необходимо отметить, что параллельные проекции, разновидностью которых являются аксонометрические и, в том числе, изометрические проекции, делятся также на ортогональные (перпендикулярные), с направлением проекции перпендикулярным к плоскости проекции, и косоугольные, с углом между направлением и плоскостью, отличным от прямого. По советским стандартам (см. ниже) аксонометрические проекции могут быть и ортогональными, и косоугольными[1]. По западным же стандартам, аксонометрические проекции являются только ортогональными, а косоугольные проекции рассматриваются отдельно.[источник не указан 1314 дней] В результате, по западным стандартам изометрическая проекция определяется более узко и, помимо равенства масштабов по осям, включает условие равенства 120° углов между проекциями любой пары осей. Во избежание путаницы далее, если не указано иное, под изометрической проекцией будет подразумеваться только прямоугольная изометрическая проекция.

Стандартные изометрические проекции[1]

Расположение осей координат в изометрических проекциях…
...прямоугольной
...косоугольной фронтальной
...косоугольной горизонтальной

Прямоугольная (ортогональная) изометрическая проекция

В прямоугольной изометрической проекции аксонометрические оси образуют между собой углы в 120°, ось Z' направлена вертикально. Коэффициенты искажения () имеют числовое значение . Как правило, для упрощения построений изометрическую проекцию выполняют без искажений по осям, то есть коэффициент искажения принимают равным 1, в этом случае получают увеличение линейных размеров в раза.

Косоугольная фронтальная изометрическая проекция

Ось Z' направлена вертикально, угол между осью X' и Z' равен 90°, ось Y' с углом наклона 135° (допускается 120° и 150°) от оси Z'.

Фронтальная изометрическая проекция выполняется по осям X', Y' и Z' без искажения.

Кривые параллельные фронтальной плоскости проецируются без искажений.

Косоугольная горизонтальная изометрическая проекция

Ось Z' направлена вертикально, между осью Z' и осью Y' угол наклона равен 120° (допускается 135° и 150°), при этом сохраняется угол между осями X' и Y' равным 90°.

Горизонтальную изометрическую проекцию выполняют без искажения по осям X', Y' и Z'.

Кривые, параллельные горизонтальной плоскости[2] проецируются без искажений.

Визуализация

Изометрический вид объекта можно получить, выбрав направление обзора таким образом, чтобы углы между проекцией осей x, y, и z были одинаковы и равны 120°. К примеру, если взять куб, это можно выполнить направив взгляд на одну из граней куба, после чего повернув куб на ±45° вокруг вертикальной оси и на ±arcsin (tan 30°) ≈ 35.264° вокруг горизонтальной оси. Обратите внимание: на иллюстрации изометрической проекции куба контур проекции образует правильный шестиугольник — все рёбра равной длины и все грани равной площади.

Подобным же образом изометрический вид может быть получен, к примеру, в редакторе трёхмерных сцен: начав с камерой, выровненной параллельно полу и координатным осям, её нужно повернуть вниз на ≈35.264° вокруг горизонтальной оси и на ±45° вокруг вертикальной оси.

Другой путь визуализации изометрической проекции заключается в рассмотрении вида кубической комнаты с верхнего угла с направлением взгляда в противолежащий нижний угол. Ось x здесь направлена диагонально вниз и вправо, ось y — диагонально вниз и влево, ось z — прямо вверх. Глубина также отражается высотой картинки. Линии, нарисованные вдоль осей, имеют угол 120° между собой.

Матричные преобразования

Имеется 8 различных вариантов получения изометрической проекции в зависимости от того, в какой октант смотрит наблюдатель. Изометрическое преобразование точки в трёхмерном пространстве в точку на плоскости при взгляде в первый октант может быть математически описано с помощью матриц поворота следующим образом. Вначале, как объяснено в разделе Визуализация, выполняется поворот вокруг горизонтальной оси (здесь x) на α = arcsin (tan 30°) ≈ 35.264° и вокруг вертикальной оси (здесь y) на β = 45°:

Затем применяется ортогональная проекция на плоскость x-y:

Другие семь возможных видов получаются поворотом к противостоящим сторонам и/или инверсией направления взгляда.[3]

Ограничения аксонометрической проекции

Изометрический рисунок с голубым шаром на два уровня выше красного

Как и в других видах параллельных проекций, объекты в аксонометрической проекции не выглядят больше или меньше при приближении или удалении от наблюдателя. Это полезно в архитектурных чертежах и удобно в спрайто-ориентированных компьютерных играх, но, в отличие от перспективной (центральной) проекции, приводит к ощущению искривления, поскольку наши глаза или фотография работают иначе.

Это также легко приводит к ситуациям, когда глубину и высоту невозможно оценить, как показано на иллюстрации справа. В этом изометрическом рисунке голубой шар на два уровня выше красного, но это нельзя увидеть, если смотреть только на левую половину картинки. Если выступ, на котором находится голубой шар, расширить на один квадрат, то он окажется точно рядом с квадратом, на котором находится красный шар, создавая оптическую иллюзию, будто оба шара на одном уровне.

Дополнительная проблема, специфичная для изометрической проекции — сложность определения, какая сторона объекта наблюдается. При отсутствии теней и для объектов, которые относительно перпендикулярны и соразмерны, сложно определить, какая сторона является верхней, нижней или боковой. Это происходит из-за приблизительно равных по размеру и площади проекций такого объекта.

Большинство современных компьютерных игр избегают этого за счёт отказа от аксонометрической проекции в пользу перспективного трёхмерного рендеринга. Однако эксплуатация проекционных иллюзий популярна в оптическом искусстве — таком, как работы из серии «невозможной архитектуры» Эшера. Водопад (1961) — хороший пример, в котором строение в основном изометрическое, в то время как блеклый фон использует перспективную проекцию. Другое преимущество заключается в том, что в черчении даже новички легко могут строить углы в 60° с помощью только циркуля и линейки.

Изометрическая проекция в компьютерных играх и пиксельной графике

Рисунок телевизора в почти-изометрической пиксельной графике. У пиксельного узора видна пропорция 2:1

В области компьютерных игр и пиксельной графики аксонометрическая проекция была весьма популярна в силу лёгкости, с которой двухмерные спрайты и плиточная графика (англ.) могли быть использованы для представления трёхмерной игровой среды — поскольку во время перемещения по игровому полю объекты не меняют размер, компьютеру не требуется масштабировать спрайты или выполнять вычисления, необходимые для моделирования визуальной перспективы. Это позволяло старым 8-битным и 16-битным игровым системам (и, позднее, портативным игровым системам) легко отображать большие трёхмерные пространства. И хотя неразбериха с глубиной (см. выше) иногда могла быть проблемой, хороший дизайн игры способен её смягчить. С приходом более мощных графических систем аксонометрическая проекция стала терять свои позиции.

Проекция в компьютерных играх обычно несколько отличается от «истинной» изометрической в силу ограничений растровой графики — линии по осям x и y не имели бы аккуратного пиксельного узора, если бы рисовались под углом в 30° к горизонтали. Хотя современные компьютеры могут устранять эту проблему с помощью сглаживания, ранее компьютерная графика не поддерживала достаточную цветовую палитру или не располагала достаточной мощностью процессоров для его выполнения. Вместо этого использовалась пропорция пиксельного узора 2:1 для рисования осевых линий x и y, в результате чего эти оси располагались под углом arctan 0,5 ≈ 26,565° к горизонтали. (Игровые системы с неквадратными пикселями могли, однако, приводить к другим углам, включая полностью изометрические). Поскольку здесь из трёх углов между осями (116,565°, 116,565°, 126,87°) равны только два, такой вид проекции более точно характеризуется как вариация диметрической проекции. Однако большинство представителей сообществ компьютерных игр и растровой графики продолжает называть эту проекцию «изометрической перспективой». Также, часто используются термины «вид 3/4 (англ.)» и «2.5D».

Термин применялся и к играм, не использующим пропорцию 2:1, общую для многих компьютерных игр. Fallout[4] и SimCity 4[5], в которых используется триметрическая проекция, были отнесены к «изометрическим». Игры с косоугольной проекцией, такие как The Legend of Zelda: A Link to the Past[6] и Ultima Online[7], а также игры с перспективной проекцией с видом «с воздуха» (англ.)русск., такие как The Age of Decadence (англ.)[8] и Silent Storm[9], также иногда относят к изометрическим или «псевдо-изометрическим».

Кадр из игры «echochrome»

Интересный пример использования особенностей изометрической проекции наблюдается в игре echochrome (яп. 無限回廊 муген кайро:?). Слоган игры — «В этом мире то, что ты видишь, становится реальностью». Смысл игры заключается в том, что иллюзия, возникающая при взгляде на изометрически построенный трёхмерный уровень с определённой точки, перестаёт быть иллюзией. Например, если посмотреть на уровень таким образом, чтобы площадки, находящиеся на разной высоте, выглядели так, будто они находятся на одной и той же высоте (см. изображение с синим и красным шарами из предыдущего раздела), игрой они будут расцениваться как находящиеся на одной высоте, и человек (игрок) сможет запросто «перешагнуть» с одной площадки на другую. Затем, если повернуть карту уровня и посмотреть на конструкцию так, чтобы было отчётливо видно разницу в высоте, можно понять, что в действительности человек «перешагнул» на другую высоту, пользуясь тем, что изометрическая иллюзия на какой-то момент стала реальностью. На приведённом в качестве иллюстрации кадре из игры положение площадки, находящейся вверху лестницы, можно представить двояко: в одном случае она находится на одной высоте с площадкой, на которой находится игрок (можно перешагнуть), а в другом случае — под ней (можно спрыгнуть через чёрное отверстие). Оба случая будут одновременно являться правдой. Очевидно, этот эффект достигается отсутствием перспективы в изометрии.

История изометрических компьютерных игр

Q*bert (1982), одна из первых игр с изометрической графикой

Первыми играми, использующими изометрическую проекцию, были аркадные игры начала 1980-х: так, Q*bert[10] и Zaxxon (англ.)[11] выпущены в 1982 году. Q*bert показывает статичную пирамиду, нарисованную в изометрической перспективе, по которой должен прыгать управляемый игроком персонаж. Zaxxon предлагает прокручиваемые изометрические уровни, над которыми летает управляемый игроком самолётик. Год спустя, в 1983 году, была выпущена аркадная игра Congo Bongo (англ.)[12], работавшая на тех же игровых автоматах, что и Zaxxon. В этой игре персонаж перемещается по большим изометрическим уровням, включающим трёхмерные подъёмы и спуски. То же самое предлагается и в аркадной игре Marble Madness (1984).

С выходом Ant Attack (англ.) (1983) для ZX Spectrum изометрические игры перестали быть изюминкой только аркадных игровых автоматов и пришли также и в домашние компьютеры. Журнал CRASH присудил этой игре 100 % в категории «графика» за новую «трёхмерную» технологию.[13] Год спустя для ZX была выпущена игра Knight Lore, которая расценивается как революционное произведение[14], определившее последующий жанр изометрических квестовых игр[15]. На домашних компьютерах было отмечено столько изометрических игр-последователей Knight Lore, что эта игра стала считаться вторым наиболее клонируемым образцом программного обеспечения после текстового редактора WordStar (англ.).[16] Среди клонов большой успех имела игра Head Over Heels (1987)[17]. Однако, изометрическая перспектива не ограничивалась только аркадами и квестовыми играми — например, стратегическая игра Populous (1989) также использовала изометрическую перспективу.

На протяжении 1990-х некоторые очень успешные игры вроде Civilization II и Diablo использовали фиксированную изометрическую перспективу. С приходом 3D ускорителей на персональные компьютеры и игровые консоли игры с трёхмерной перспективой в основном переключились на полноценную трёхмерность вместо изометрической перспективы. Это можно видеть в преемницах вышеназванных игр — начиная с Civilization IV в этой серии используется полная трёхмерность. Diablo II, как и ранее, использует фиксированную перспективу, но опционально применяет перспективное масштабирование спрайтов на расстоянии, получая псевдо-трёхмерную перспективу.[18]

См. также: Категория:Компьютерные игры с изометрической графикой

Примечания

Ссылки

Introduction to 3 Dimensional graphics (англ.). Blueprint project. IDER group, Manufactuing Systems Engineering Centre, University of Hertfordshire. — Пояснения и учебник по рисованию в изометрической перспективе из Хертфорширдского университета.(недоступная ссылка — история) Проверено 29 сентября 2008.
Herbert Glarner. Isometric Projection (англ.) (19 марта 2007). Архивировано из первоисточника 19 февраля 2012. Проверено 29 сентября 2008.
PixelDam (англ.). — A collaborative pixelart community. Архивировано из первоисточника 19 февраля 2012. Проверено 29 сентября 2008.
Tom Gersic. Rendering Isometric Tiles in Blender 3D (англ.). — Учебник с примерами по созданию изометрических плиток в программе Blender 3D. Архивировано из первоисточника 19 февраля 2012. Проверено 29 сентября 2008.

Литература

Богданов В. Н., Малежик И. Ф., Верхола А. П. и др. Справочное руководство по черчению. — М.: Машиностроение, 1989. — С. 864. — ISBN 5-217-00403-7
Фролов С. А. Начертательная геометрия. — 2-е изд., перераб. и доп. — М.: Машиностроение, 1983. — С. 240.

dic.academic.ru

ПРЯМОУГОЛЬНАЯ ИЗОМЕТРИЧЕСКАЯ ПРОЕКЦИЯ

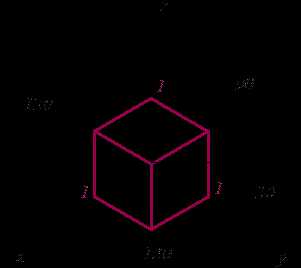В прямоугольной изометрической проекции оси координат расположены под одинаковым углом друг к другу - 120º (рис 11.1). На практике коэффициенты искажения по осям принимают равным единице, поэтому при построении изометрии вдоль координатных осей откладывают натуральные размеры предмета, например, на рис. 11.1 – куб. На рис. 11.2 показано построение шестигранной призмы.

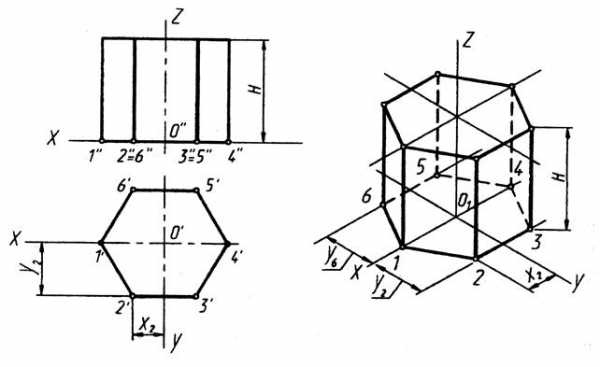
Рис. 11.2

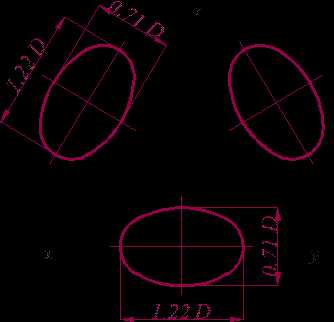Рис. 11.3

Окружности в аксонометрических проекциях представляют собой эллипсы. В прямоугольной изометрии все три эллипса одинаковы по форме, равны друг другу, но расположены различно (рис 11.3) . Их большая ось всегда располагаются перпендикулярно отсутствующей в данной плоскости аксонометрической оси, а малая ось - параллельна ей. Например, в плоскости V (x, z) большая ось перпендикулярна y, а малая ось - параллельна ей. Размеры осей эллипса приведены на рис.11.3, где D – диаметр окружности.

Построение эллипса сравнительно сложно, поэтому его заменяют овалом. Овал - это кривая, по очертанию похожая на эллипс, но строится при помощи циркуля. На рис.11.4 показано построение овала в плоскости H (x, y). Из центра будущего овала строится окружность заданного диаметра D, большая и малая оси. Пересечение окружности с малой осью даст точки О1 и О2 – центры больших дуг радиусом R= О11= О22. Дуги вычерчиваются из центров от точек 1 и 2 соответственно до пересечения с окружностью. Пересечение О11 и О22 с большой осью даст точки О3 и О4 – центры малых дуг радиусом r.

Рис. 11.4

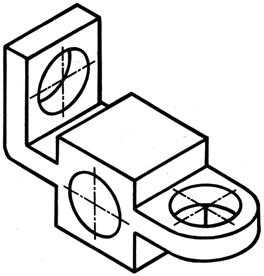Рисунок 11.5

Пример изображения детали с отверстиями в изометрии показан на рис.11.5.

Прямоугольная изометрическая проекция

В изометрической проекции все коэффициенты равны между собой:

K = m = n; k2 + m2 + n2 = 2.

Тогда

Зk2 = 2,

откуда

Следовательно, при построении изометрической проекции размеры предмета, откладываемые по аксонометрическим осям, умножают на 0,82. Такой перерасчет размеров неудобен. Поэтому изометрическую проекцию для упрощения, как правило, выполняют без уменьшения размеров (искажения) по осям х, у, z, т. е. используют приведенный коэффициент искажения, который принимают равным 1. Получаемое при этом изображение предмета в изометрической проекции имеет несколько большие размеры, чем в действительности. Увеличение в этом случае составляет 22% (выражается числом 1,22 = 1: 0,82).

Каждый отрезок, направленный по осям х, у, z или параллельно им, сохраняет свою величину.

Расположение осей изометрической проекции показано на рисунке 4. На рисунках 5а, 6а показаны ортогональные, а на рисунках 5б, 6б — изометрические проекции точки А и отрезка А В.

Шестигранная призма в изометрии. Построение шестигранной призмы по данному чертежу в системе ортогональных проекций (слева на рис. 7) приведено на рисунке 189. На изометрической оси z откладывают высоту Н, проводят линии, параллельные осям х и у. Отмечают на линии, параллельной оси х, положение точек 1 и 4.

Для построения точки 2 определяют координаты этой точки на чертеже — х2 и у2 — и, откладывая эти координаты на аксонометрическом изображении, строят точку 2. Таким же образом строят точки 3, 5 и 6.

Построение точки верхнего основания соединяют между собой, проводят ребро из точки 1 до пересечения с осью x,затем — ребра из точек 2, 3, 6. Ребра нижнего основания проводят параллельно ребрам верхнего. Построение точки А, расположенной на боковой грани, по координатам хА (или уА) и zA очевидно из рисунка 7.

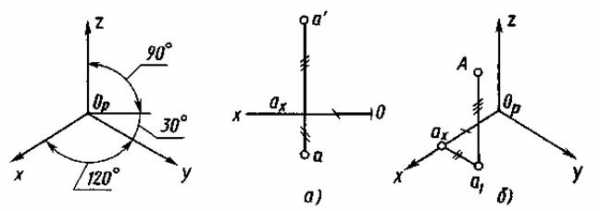
Рис. 4Рис. 5

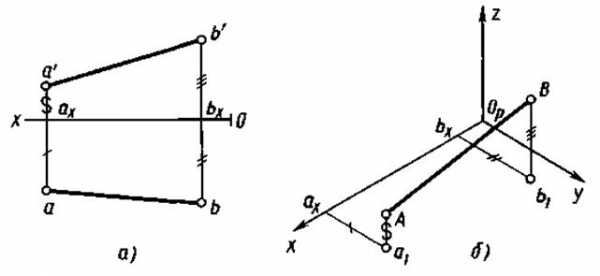
Рис. 6

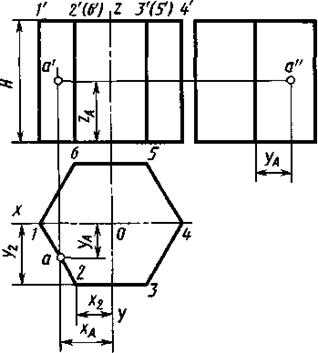
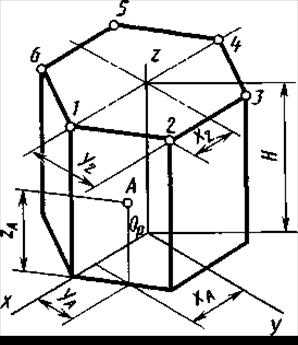
Рис. 7

Прямоугольная диметрическая проекция

Коэффициенты искажения в диметрической проекции выбирают следующими:

k = n; m =1/2 k.

В целях упрощения построений, как и в изометрических проекциях, приведенный коэффициент искажения по осям хи z принимают равным 1; по оси укоэффициент искажения равен 0,5. По осям х и z или параллельно им все размеры откладывают в натуральную величину, по оси у размеры уменьшают вдвое.

Увеличение в этом случае составляет 6% (выражается числом 1,06 = 1:0,94).

Расположение осей Ох и Оу в диметрическои проекции показано на рисунке 8. С достаточной для практических целей точностью оси х и у строят по тангенсам углов:

tg 7°10' = 1/8; tg 42°25' = 7/8.

Продолжение оси у за центр Ор является биссектрисой угла xOpz, что также может быть использовано для построения оси у.

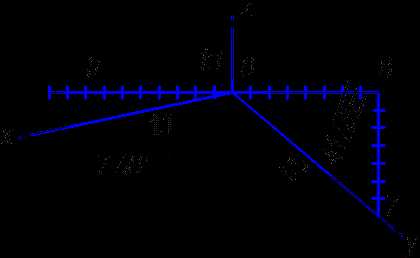
Рис. 8

Аксонометрические изображения окружности

Окружности в аксонометрической проекции приведены на рисунке 9 (построение предложено Ю.Б. Ивановым), в диметрическои — на рисунке 10 с указанием соответствующих значений величин осей эллипсов для приведенных коэффициентов искажения, равных 1.

Большая ось эллипсов расположена под утлом 90° для эллипсов, лежащих:

в плоскости xOz — к оси у,

в плоскости yOz — к оси х,

в плоскости хОу — к оси z.

При выполнении аксонометрического изображения от руки (какна рис. 9., 10) построение эллипсов, как в изометрии, так и в диметрии, выполняют по 8 точкам. Например, по точкам 1, 2, 3, 4, 5, 6, 7 и 8 (рис. 9). Точки 7, 2, 3 и 4 находят на соответствующих аксонометрических осях, а точки 5, 6, 7 и 8 строят по величинам соответствующих большой и малой осей эллипса.

При выполнении же аксонометрического изображения чертежным инструментом построение эллипсов в диметрическойпроекции также производят по 8 точкам, а эллипсы в изометрической проекции можнозаменять овалами и строить их следующим образом.

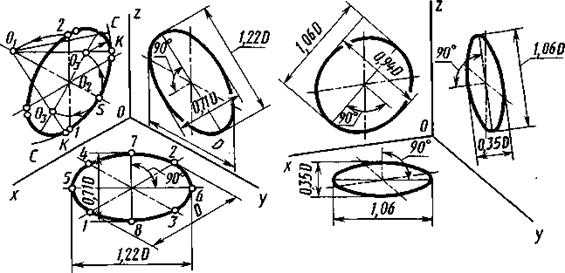
Рис. 9Рис. 10

Построение показано на рисунке 9 на примере эллипса, лежащего в плоскости xOz. Из точки 1 как из центра делают засечку радиусом R = D на продолжении малой оси эллипса в точке О1 (строят также аналогичным образом и симметричную ей точку, которая на чертеже не показана). Из точки О1 как из центра проводят дугу CSC радиуса D, которая является одной из дуг, составляющих контур эллипса. Из точки О2 как из центра проводят дугу радиуса O2S до пересечения с большой осью эллипса в точках О3. Проводя через точки О1, О3 прямую, находят в пересечении с дугой CSC точку К, которая определяет О3К — величину радиуса замыкающей дуги овала. Точки К являются также точками сопряжения дуг, составляющих овал.

Аксонометрия цилиндра. Аксонометрические изображения цилиндра определяются аксонометрическими изображениями окружностей его оснований. Построение в изометрии цилиндра высотой Н по ортогональному чертежу (рис. 11 слева) и точки Сна его боковой поверхности показано на рисунке 11 справа.

Аксонометрическое изображение сферы и способ вписывания сферических поверхностей. В прямоугольной аксонометрии поверхность сферы проецируется на аксонометрическую плоскость проекций в виде круга. Это позволяет использовать сферу для построения аксонометрических проекций тех фигур, в которые могут быть вписаны сферические поверхности. Так, например, аксонометрия поверхности вращения в этом случае может быть построена как огибающая сфер, вписанных в эту поверхность.

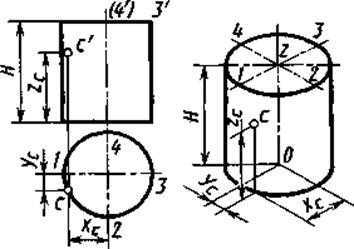
Рис. 11

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:

zdamsam.ru

Изометрическая проекция — WiKi

Изометри́ческая прое́кция (др.-греч. ἴσος «равный» + μετρέω «измеряю») — это разновидность аксонометрической проекции, при которой в отображении трёхмерного объекта на плоскость коэффициент искажения (отношение длины спроецированного на плоскость отрезка, параллельного координатной оси, к действительной длине отрезка) по всем трём осям один и тот же. Слово «изометрическая» в названии проекции пришло из греческого языка и означает «равный размер», отражая тот факт, что в этой проекции масштабы по всем осям равны. В других видах проекций это не так.

Стол в прямоугольной изометрической проекции

Необходимо отметить, что параллельные проекции, разновидностью которых являются аксонометрические и, в том числе, изометрические проекции, делятся также на ортогональные (перпендикулярные), с направлением проекции перпендикулярным к плоскости проекции, и косоугольные, с углом между направлением и плоскостью, отличным от прямого. По советским стандартам (см. ниже) аксонометрические проекции могут быть и ортогональными, и косоугольными[1]. В результате, по западным стандартам изометрическая проекция определяется более узко и, помимо равенства масштабов по осям, включает условие равенства 120° углов между проекциями любой пары осей. Во избежание путаницы далее, если не указано иное, под изометрической проекцией будет подразумеваться только прямоугольная изометрическая проекция.

Стандартные изометрические проекции[1]

...прямоугольной
...косоугольной фронтальной
...косоугольной горизонтальной

Прямоугольная (ортогональная) изометрическая проекция

В прямоугольной изометрической проекции аксонометрические оси образуют между собой углы в 120°, ось Z' направлена вертикально. Коэффициенты искажения (kx,ky,kz{\displaystyle k_{x},k_{y},k_{z}} ) имеют числовое значение 23≈0,82{\displaystyle {\sqrt {\frac {2}{3}}}\approx 0,82} . Как правило, для упрощения построений изометрическую проекцию выполняют без искажений по осям, то есть коэффициент искажения принимают равным 1, в этом случае получают увеличение линейных размеров в 10,82≈1,22{\displaystyle {\frac {1}{0,82}}\approx 1,22} раза.

Приближённо аксонометрические оси прямоугольной проекции можно построить, если принять tg 30°=4/7 (0,577 и 0,571 соотв.).

Косоугольная фронтальная изометрическая проекция

Фронтальная изометрическая проекция выполняется по осям X', Y' и Z' без искажения.

Кривые, параллельные фронтальной плоскости, проецируются без искажений.

Косоугольная горизонтальная изометрическая проекция

Горизонтальную изометрическую проекцию выполняют без искажения по осям X', Y' и Z'.

Кривые, параллельные горизонтальной плоскости[2] проецируются без искажений.

Стоит отметить, что, поскольку ортогональный трёхгранник невозможно повернуть так, чтобы два его ребра были бы видны взаимно-перпендикулярными, и третье ребро при этом не проецировалась бы в точку, все проекции, в которых видны все три оси, но угол на чертеже между к-н двумя — прямой (здесь это вторая и третья из приведённых), строго говоря, показывают «то, чего не бывает».

К счастью, глаз человека довольно успешно корректирует такие погрешности при изображении реальных объектов, и потому они допустимы ради простоты построения чертежа.

Визуализация

Изометрический вид объекта можно получить, выбрав направление обзора таким образом, чтобы углы между проекцией осей x, y, и z были одинаковы и равны 120°. К примеру, если взять куб, это можно выполнить направив взгляд на одну из граней куба, после чего повернув куб на ±45° вокруг вертикальной оси и на ±arcsin (tan 30°) ≈ 35,264° вокруг горизонтальной оси. Обратите внимание: на иллюстрации изометрической проекции куба контур проекции образует правильный шестиугольник — все рёбра равной длины и все грани равной площади.

Матричные преобразования

Имеется 8 различных вариантов получения изометрической проекции в зависимости от того, в какой октант смотрит наблюдатель. Изометрическое преобразование точки ax,y,z{\displaystyle a_{x,y,z}} в трёхмерном пространстве в точку bx,y{\displaystyle b_{x,y}} на плоскости при взгляде в первый октант может быть математически описано с помощью матриц поворота следующим образом. Вначале, как объяснено в разделе Визуализация, выполняется поворот вокруг горизонтальной оси (здесь x) на α = arcsin (tan 30°) ≈ 35,264° и вокруг вертикальной оси (здесь y) на β = 45°:

[cxcycz]=[1000cos⁡αsin⁡α0−sin⁡αcos⁡α][cos⁡β0−sin⁡β010sin⁡β0cos⁡β][axayaz]=16[30−31212−22][axayaz]{\displaystyle {\begin{bmatrix}\mathbf {c} _{x}\\\mathbf {c} _{y}\\\mathbf {c} _{z}\\\end{bmatrix}}={\begin{bmatrix}1&0&0\\0&{\cos \alpha }&{\sin \alpha }\\0&{-\sin \alpha }&{\cos \alpha }\\\end{bmatrix}}{\begin{bmatrix}{\cos \beta }&0&{-\sin \beta }\\0&1&0\\{\sin \beta }&0&{\cos \beta }\\\end{bmatrix}}{\begin{bmatrix}\mathbf {a} _{x}\\\mathbf {a} _{y}\\\mathbf {a} _{z}\\\end{bmatrix}}={\frac {1}{\sqrt {6}}}{\begin{bmatrix}{\sqrt {3}}&0&-{\sqrt {3}}\\1&2&1\\{\sqrt {2}}&-{\sqrt {2}}&{\sqrt {2}}\\\end{bmatrix}}{\begin{bmatrix}\mathbf {a} _{x}\\\mathbf {a} _{y}\\\mathbf {a} _{z}\\\end{bmatrix}}}

Затем применяется ортогональная проекция на плоскость x-y:

[bxby0]=[100010000][cxcycz]{\displaystyle {\begin{bmatrix}\mathbf {b} _{x}\\\mathbf {b} _{y}\\0\\\end{bmatrix}}={\begin{bmatrix}1&0&0\\0&1&0\\0&0&0\\\end{bmatrix}}{\begin{bmatrix}\mathbf {c} _{x}\\\mathbf {c} _{y}\\\mathbf {c} _{z}\\\end{bmatrix}}}

Ограничения аксонометрической проекции

Изометрический рисунок с голубым шаром на два уровня выше красного

Как и в других видах параллельных проекций, объекты в аксонометрической проекции не выглядят больше или меньше при приближении или удалении от наблюдателя. Это полезно в архитектурных чертежах и удобно в спрайто-ориентированных компьютерных играх, но, в отличие от перспективной (центральной) проекции, приводит к ощущению искривления, поскольку человеческий глаз или фотография работают иначе.

Изометрическая проекция в компьютерных играх и пиксельной графике

Рисунок телевизора в почти-изометрической пиксельной графике. У пиксельного узора видна пропорция 2:1

В области компьютерных игр и пиксельной графики аксонометрическая проекция была весьма популярна в силу лёгкости, с которой двухмерные спрайты и плиточная графика могли быть использованы для представления трёхмерной игровой среды — поскольку во время перемещения по игровому полю объекты не меняют размер, компьютеру не требуется масштабировать спрайты или выполнять вычисления, необходимые для моделирования визуальной перспективы. Это позволяло старым 8-битным и 16-битным игровым системам (и, позднее, портативным игровым системам) легко отображать большие трёхмерные пространства. И хотя неразбериха с глубиной (см. выше) иногда могла быть проблемой, хороший дизайн игры способен её смягчить. С приходом более мощных графических систем аксонометрическая проекция стала терять свои позиции.

Проекция в компьютерных играх обычно несколько отличается от «истинной» изометрической в силу ограничений растровой графики — линии по осям x и y не имели бы аккуратного пиксельного узора, если бы рисовались под углом в 30° к горизонтали. Хотя современные компьютеры могут устранять эту проблему с помощью сглаживания, ранее компьютерная графика не поддерживала достаточную цветовую палитру или не располагала достаточной мощностью процессоров для его выполнения. Вместо этого использовалась пропорция пиксельного узора 2:1 для рисования осевых линий x и y, в результате чего эти оси располагались под углом arctg 0,5 ≈ 26,565° к горизонтали. (Игровые системы с неквадратными пикселями могли, однако, приводить к другим углам, включая полностью изометрические[4]). Поскольку здесь из трёх углов между осями (116,565°, 116,565°, 126,87°) равны только два, такой вид проекции более точно характеризуется как вариация диметрической проекции. Однако большинство представителей сообществ компьютерных игр и растровой графики продолжает называть эту проекцию «изометрической перспективой». Также, часто используются термины «вид 3/4 (англ.)» и «2.5D».

Термин применялся и к играм, не использующим пропорцию 2:1, общую для многих компьютерных игр. Fallout[5] и SimCity 4[6], в которых используется триметрическая проекция, были отнесены к «изометрическим». Игры с косоугольной проекцией, такие как The Legend of Zelda: A Link to the Past[7] и Ultima Online[8], а также игры с перспективной проекцией с видом «с воздуха» (англ.)русск., такие как The Age of Decadence (англ.)[9] и Silent Storm[10], также иногда относят к изометрическим или «псевдо-изометрическим».

Кадр из игры «echochrome»

Интересный пример использования особенностей изометрической проекции наблюдается в игре echochrome (яп. 無限回廊 муген кайро:). Слоган игры — «В этом мире то, что ты видишь, становится реальностью». Смысл игры заключается в том, что иллюзия, возникающая при взгляде на изометрически построенный трёхмерный уровень с определённой точки, перестаёт быть иллюзией. Например, если посмотреть на уровень таким образом, чтобы площадки, находящиеся на разной высоте, выглядели так, будто они находятся на одной и той же высоте (см. изображение с синим и красным шарами из предыдущего раздела), игрой они будут расцениваться как находящиеся на одной высоте, и человек (игрок) сможет запросто «перешагнуть» с одной площадки на другую. Затем, если повернуть карту уровня и посмотреть на конструкцию так, чтобы было отчётливо видно разницу в высоте, можно понять, что в действительности человек «перешагнул» на другую высоту, пользуясь тем, что изометрическая иллюзия на какой-то момент стала реальностью. На приведённом в качестве иллюстрации кадре из игры положение площадки, находящейся вверху лестницы, можно представить двояко: в одном случае она находится на одной высоте с площадкой, на которой находится игрок (можно перешагнуть), а в другом случае — под ней (можно спрыгнуть через чёрное отверстие). Оба случая будут одновременно являться правдой. Очевидно, этот эффект достигается отсутствием перспективы в изометрии.

История изометрических компьютерных игр

Q*bert (1982), одна из первых игр с изометрической графикой

Первыми играми, использующими изометрическую проекцию, были аркадные игры начала 1980-х: так, Q*bert[11] и Zaxxon[12] выпущены в 1982 году. Q*bert показывает статичную пирамиду, нарисованную в изометрической перспективе, по которой должен прыгать управляемый игроком персонаж. Zaxxon предлагает прокручиваемые изометрические уровни, над которыми летает управляемый игроком самолётик. Год спустя, в 1983 году, была выпущена аркадная игра Congo Bongo (англ.)[13], работавшая на тех же игровых автоматах, что и Zaxxon. В этой игре персонаж перемещается по большим изометрическим уровням, включающим трёхмерные подъёмы и спуски. То же самое предлагается и в аркадной игре Marble Madness (1984).

С выходом Ant Attack (англ.) (1983) для ZX Spectrum изометрические игры перестали быть изюминкой только аркадных игровых автоматов и пришли также и в домашние компьютеры. Журнал CRASH присудил этой игре 100 % в категории «графика» за новую «трёхмерную» технологию.[14] Год спустя для ZX была выпущена игра Knight Lore, которая расценивается как революционное произведение[15], определившее последующий жанр изометрических квестовых игр[16]. На домашних компьютерах было отмечено столько изометрических игр-последователей Knight Lore, что эта игра стала считаться вторым наиболее клонируемым образцом программного обеспечения после текстового редактора WordStar (англ.).[17] Среди клонов большой успех имела игра Head Over Heels (1987)[18]. Однако, изометрическая перспектива не ограничивалась только аркадами и квестовыми играми — например, стратегическая игра Populous (1989) также использовала изометрическую перспективу.

Примечания

↑ 1 2 По ГОСТ 2.317-69 — Единая система конструкторской документации. Аксонометрические проекции.
↑ Здесь горизонтальной называется плоскость, перпендикулярная оси Z (которая является прообразом оси Z').
↑ Ingrid Carlbom, Joseph Paciorek. Planar Geometric Projections and Viewing Transformations // ACM Computing Surveys (CSUR) : журнал. — ACM, декабрь 1978. — Т. 10, № 4. — С. 465—502. — ISSN 0360-0300. — DOI:10.1145/356744.356750.
↑ Так, в распространённом разрешении CGA/VGA 320×200 этот угол равняется arctg 0,6 ≈ 30,96°.
↑ Jeff Green. GameSpot Preview: Arcanum (англ.) (недоступная ссылка — история). GameSpot (29 февраля 2000). Проверено 29 сентября 2008. Архивировано 31 августа 2000 года.
↑ Steve Butts. SimCity 4: Rush Hour Preview (англ.). IGN (9 сентября 2003). Проверено 29 сентября 2008. Архивировано 19 февраля 2012 года.
↑ GDC 2004: The History of Zelda (англ.). IGN (25 марта 2004). Проверено 29 сентября 2008. Архивировано 19 февраля 2012 года.
↑ Dave Greely, Ben Sawyer. Has Origin Created the First True Online Game World? (англ.). Gamasutra (19 августа 1997). Проверено 29 сентября 2008. Архивировано 19 февраля 2012 года.
↑ Age of Decadence (англ.). Iron Tower Studios. Проверено 29 сентября 2008. Архивировано 19 февраля 2012 года.
↑ Steve O’Hagan. PC Previews: Silent Storm (англ.). GamesRadar—CVG (7 августа 2003). Проверено 29 сентября 2008. Архивировано 19 февраля 2012 года.
↑ Q*bert (англ.) на сайте Killer List of Videogames
↑ Zaxxon (англ.) на сайте Killer List of Videogames
↑ Congo Bongo (англ.) на сайте Killer List of Videogames
↑ Soft Solid 3D Ant Attack // CRASH : журнал. — февраль 1984. — № 1.
↑ Ultimate Play The Game — Company Lookback // Retro Micro Games Action — The Best of gamesTM (англ.) Retro. — Highbury Entertainment, 2006. — Т. 1. — С. 25.
↑ Steven Collins. Game Graphics During the 8-bit Computer Era // ACM SIGGRAPH. Computer Graphics. — май 1998. — Т. 32, № 2.
↑ Krikke J. Axonometry: a matter of perspective // IEEE. Computer Graphics and Applications. — июль-август 2000. — Т. 20, № 4. — С. 7—11. — DOI:10.1109/38.851742.
↑ Looking for an old angle // CRASH : журнал. — апрель 1988. — № 51.
↑ Diablo II Nears Completion As Blizzard Prepares For Final Phase Of Beta Testing (недоступная ссылка — история). Market Wire (май 2000). Проверено 29 сентября 2008. Архивировано 10 июля 2012 года.

Ссылки

Introduction to 3 Dimensional graphics (англ.). Blueprint project (недоступная ссылка — история). IDER group, Manufactuing Systems Engineering Centre, University of Hertfordshire. — Пояснения и учебник по рисованию в изометрической перспективе из Хертфорширдского университета. Проверено 29 сентября 2008. Архивировано 28 октября 2000 года.
Herbert Glarner. Isometric Projection (англ.) (19 марта 2007). Проверено 29 сентября 2008. Архивировано 19 февраля 2012 года.
PixelDam (англ.). — A collaborative pixelart community. Проверено 29 сентября 2008. Архивировано 19 февраля 2012 года.
Tom Gersic. Rendering Isometric Tiles in Blender 3D (англ.). — Учебник с примерами по созданию изометрических плиток в программе Blender 3D. Проверено 29 сентября 2008. Архивировано 19 февраля 2012 года.

Литература

Богданов В. Н., Малежик И. Ф., Верхола А. П. и др. Справочное руководство по черчению. — М.: Машиностроение, 1989. — С. 864. — ISBN 5-217-00403-7.
Фролов С. А. Начертательная геометрия. — 2-е изд., перераб. и доп. — М.: Машиностроение, 1983. — С. 240.

ru-wiki.org

Прямоугольная изометрическая проекция.

Аксонометрия. Аксонометрические проекции.

Расположение аксонометрических осей показано на рисунке. Все три оси образуют между собой равные углы в

1200. Ось OZ располагается вертикально.

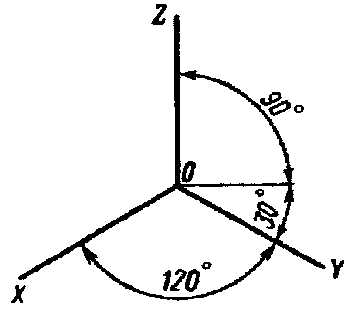
Аксонометрия. Изометрия.

Коэффициент искажения по все трем осям равен 0,82. На практике прямоугольную изометрическую проекцию

обычно строят без сокращения размеров по осям - все размеры, параллельные осям, принимают с коэффициентом

искажения равным единице.

Получается изображение, подобное точной проекции, но увеличенное в 1, 22 раза. На рисунке показаны

направления осей эллипсов, изображающих окружности, расположенные в плоскостях, параллельных координатным

плоскостям.

Большие оси АВ перпендикулярны к соответствующим аксонометрическим осям. Малые оси CD

перпендикулярны к АВ и параллельны соответствующим аксонометрическим осям. Все три эллипса равны.

Размеры осей эллипсапо отношению к диаметруdокружности:

При построенииточной проекции с коэффициентомискажения0,82 АВ = d; CD = 0,58d.

При построении без сокращения размеров по всем осям АВ = 1,22d; CD = 0,71d.

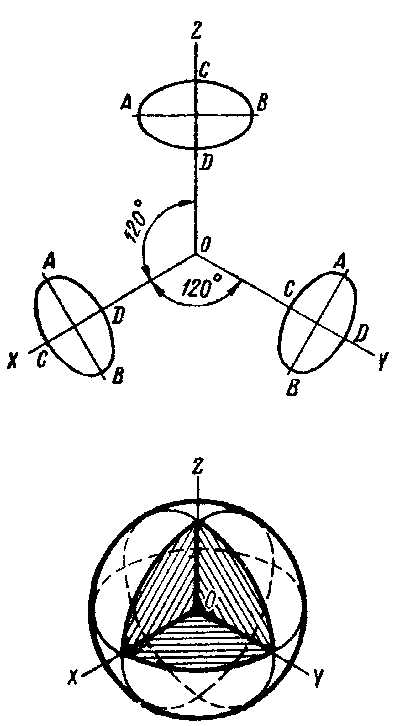
Аксонометрия. Изометрия шара.

Изометрия шара показана на рисунке. Внешний контур шара является окружностью. При построении точной

проекции R = d/2.При построении с коэффициентом искажения, приведенным к единице, R = 1,22d/2.

d- диаметр шара.

Штриховка разрезов в аксонометрии.

Линии штриховки сечений наносят параллельно одной из диагоналей квадратов (условно изображенных), лежащих

в соответствующих координатных плоскостях. Стороны условного квадрата параллельны аксонометрическим осям.

Различные сечения одной и той же детали штрихуются с наклоном в разные стороны.

Выносные линии на чертежах в аксонометрии проводятся параллельно аксонометрическим осям. Размерные линии

проводятся параллельно измеряемому отрезку.

Аксонометрия. Изометрия.

Построение аксонометрических изображений

Переход от ортогональных проекций предмета к аксонометрическому изображению рекомендуется осуществлять в такой последовательности (рис. 161):


Рисунок 161. Построение аксонометрического изображения

1. На ортогональном чертеже размечают оси прямоугольной системы координат, к которой и относят данный предмет. Оси ориентируют так, чтобы они допускали удобное измерение координат точек предмета. Например, при построении аксонометрии тела вращения одну из координатных осей целесообразно совместить с осью тела.

2. Строят аксонометрические оси с таким расчетом, чтобы обеспечить наилучшую наглядность изображения и видимость тех или иных точек предмета.

3. По одной из ортогональных проекций предмета чертят вторичную проекцию.

4. Создают аксонометрическое изображение, для наглядности делают вырез четверти.

ГОСТ 2.317-69 определяет условности и способы нанесения размеров при построении аксонометрического изображения, основное внимание следует обратить на следующее:


Рисунок 162. Штриховка в аксонометрии

· Линии штриховки сечения в аксонометрических проекциях наносят параллельно одной из диагоналей проекций квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям.

· При нанесении размеров выносные линии проводят параллельно аксонометрическим осям, размерные линии – параллельно измеряемому отрезку.

· В аксонометрических проекциях спицы маховиков и шкивов, ребра жесткости и подобные элементы штрихуют.

Инструкция

Пусть перед вами стоит задача выполнить построение аксонометрической проекции заданного тела вращения. В первую очередь нужно соотнести данное тело с какой-либо прямоугольной системой координат. Так как дано тело вращения, то в данном случае для удобства счёта одну из осей системы координат необходимо совместить с осью тела вращения.

Теперь нужно вычертить вторую ортогональную проекцию тела, как показано на рисунке.

Затем необходимо перейти к построению аксонометрических осей. Учтите, что их нужно так располагать на листе, чтобы большей части поверхности предмета была обеспечена видимость. Для того, чтобы упростить задачу построения лучше всего будет взять координатную ось, используемую в прямоугольной изометрической проекции, изображенную на рисунке. Благодаря такому выбору, коэффициенты искажения по каждой из осей становятся равными единице. Если же делать стандартные аксонометрические оси, в которых соседние оси образуют угол в 120 градусов, то коэффициент искажения станет равен 0,82. Это создаст дополнительные сложности при изображении предмета.

Все элементы заданной фигуры необходимо спроецировать в соотношении один к одному вдоль аксонометрических осей. Для того, чтобы изображение было более наглядным, в ближайшей четверти детали делается вырез, с последующей штриховкой. Линии штриховки по правилам наносят параллельно какой-либо из диагоналей условного квадрата, лежащего в рассматриваемой координатной плоскости. Стороны этого квадрата должны быть параллельны аксонометрическим осям. В одной детали разные сечения необходимо заштриховывать с наклоном в разные стороны.

mykonspekts.ru

Прямоугольная изометрическая проекция

Производство Прямоугольная изометрическая проекция
просмотров - 463

Углы между осями х, у и z равны между собой, линейные размеры предмета͵ параллельные этим осям, искажаются одинаково (рис. 4.2).

а б

Рис. 4.2

При построении аксонометрии дробные показатели искажений усложняют расчет размеров, для его упрощения пользуются приведёнными показателям искажений: в изометрии все три показателя увеличивают в 1,22 раза (1:0,82»l,22), получая 1 (рис. 4.2, а), так, длина всех ребер куба на изображении одинаковая (рис. 4.2, б), равная 0,82 действительной длины. Для упрощения построений (как сказано выше), отрезки, параллельные аксонометрическим осям, откладываются действительной длины.

Линии штриховки сечений наносят параллельно одной из диагоналей проекции квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям («спроецированная» штриховка, рис. 4.3).

Рис. 4.3

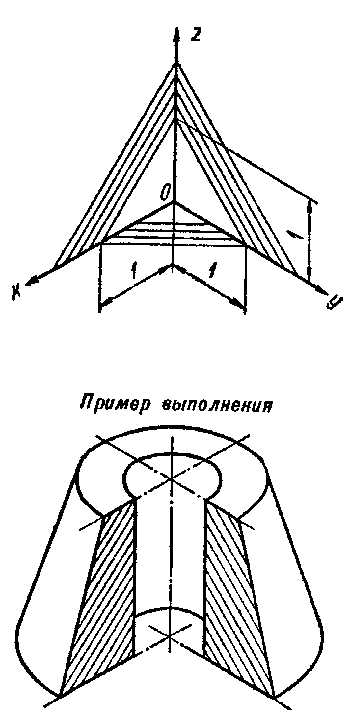
В случае если основание тела ‑ правильный многоугольник (к примеру, шестиугольник), то построенные прямоугольные изометрические проекции тела, ограниченного плоскостями, выполняют просто, а именно: построение вершин основания по координатам упрощается, провести одну из осей координат через центр основания (рис. 4.4).

Рис. 4.4

Построив изометрию основания призмы, из вершин шестиугольника основания проводим прямые, параллельные соответственно осям х', у или z'. На этих прямых от вершин основания отложим высоту призмы и получим изометриювершин другого основания призмы. Соединив эти точки прямыми, получим изометрическую проекцию призмы.

Прямоугольная изометрическая проекция окружности. В случае если построить изометрическую проекцию куба, в грани которого вписаны окружности диаметра D (рис. 4.5, а), то квадратные грани куба будут изображаться в виде ромбов, а окружности в виде эллипсов (рис.4.5, б). Малая ось CD' каждого эллипса всегда должна быть перпендикулярна большой оси А 'В'.

а б

Рис. 4.5

В случае если окружность расположена в плоскости, параллельной горизонтальной плоскости,то большая ось А'В' должна быть горизонтальной, а малая ось С'D'-вертикальной (рис. 4.5, б). В случае если окружность расположена в плоскости, параллельной фронтальной плоскости,то большая ось эллипса должна быть проведена под углом 90° к оси у.

При расположении окружности в плоскости, параллельной профильной плоскости, большая ось эллипса располагается под углом 90° к оси х'.

Рис. 4.6

Большие оси эллипсов всегда перпендикулярны соответствующим осям, а малые ‑ им параллельны.

При построении изометрической проекции окружности без сокращения по осям х', у' и z' длина большой оси эллипса берется равной 1,22 диаметра D изображаемой окружности, а длина малой оси эллипса ‑ 0,71D (рис. 4.6).

Рис.4.7

В учебных чертежах для упрощения построения вместо эллипсов рекомендуется применять овалы, очерченные дугами окружностей. Упрощенный способ построения изометрического овала приведен на рис. 4.7. Для построения овала в плоскости, параллельной горизонтальной плоскости проекций, проводим вертикальную и горизонтальную оси овала.

Из точки пересечения осей О проводим вспомогательную окружность диаметром D, равным действительной величине диаметра изображаемой окружности, и находят точки п – точки пересечения этой окружности с аксонометрическими осями х и у. Из точек m пересечения вспомогательной окружности с осью z,как из центров радиусом R1 =пт, проводим две дуги ‑ nDn и пСп окружности, принадлежащие овалу.

Из центра О радиусом ОС, равным половине малой оси овала, находим на большой оси овала АВ точки О1и О1′. Из этих точек радиусом R=O11 = O12 = О1′3 = О1′4 проводим две дуги. Точки 1, 2, 3 и 4 сопряжений дуг радиусов R и R1находим, соединяя точки m с точками О1 и О1′ и продолжая прямые до пересечения с дугами пСп и nDn. Также строим овалы, расположенные в плоскостях, параллельных фронтальной и профильной плоскостям проекций.

На рис. 4.8 приведен пример построения овалов на изометрии детали с расположением окружностей в плоскостях, параллельных горизонтальной, фронтальной и профильной плоскостям проекций.

Рис. 4.8

Построение аксонометрической проекции детали следует начинать с изображения на чертеже аксонометрических осей. Целесообразно за начало координат принимать центр симметрии, а за оси координат – оси симметрии детали.

При построении аксонометрии рекомендуется мысленно разделить деталь на простейшие геометрические тела (цилиндр, конус, призма, пирамида и т. п.). После изображения аксонометрических проекций составных элементов предмета строятся конструктивные скругления в местах их соединения.

Линии, изображающие проекции предмета͵ параллельны одноименным аксонометрическим осям, в связи с этим при построении аксонометрических проекций удобно использовать прямые, параллельные аксонометрическим осям.

Рис.4.9

Как и на комплексном чертеже, полые детали в аксонометрии рекомендуется выполнять с разрезом (рис. 4.9).

В случае если окружность неполная, то для ее изображения вычерчивают тонкой линией полный овал или эллипс, а затем обводят нужную часть овала

(рис. 4.9).

Изометрическая проекция - это... Что такое Изометрическая проекция?

Стол в прямоугольной изометрической проекции

Стандартные изометрические проекции[1]

Расположение осей координат в изометрических проекциях…
...прямоугольной
...косоугольной фронтальной
...косоугольной горизонтальной

Прямоугольная (ортогональная) изометрическая проекция

Косоугольная фронтальная изометрическая проекция

Фронтальная изометрическая проекция выполняется по осям X', Y' и Z' без искажения.

Кривые параллельные фронтальной плоскости проецируются без искажений.

Косоугольная горизонтальная изометрическая проекция

Горизонтальную изометрическую проекцию выполняют без искажения по осям X', Y' и Z'.

Кривые, параллельные горизонтальной плоскости[2] проецируются без искажений.

Визуализация

Матричные преобразования

Затем применяется ортогональная проекция на плоскость x-y:

Ограничения аксонометрической проекции

Изометрический рисунок с голубым шаром на два уровня выше красного

Изометрическая проекция в компьютерных играх и пиксельной графике

Рисунок телевизора в почти-изометрической пиксельной графике. У пиксельного узора видна пропорция 2:1

Кадр из игры «echochrome»

История изометрических компьютерных игр

Q*bert (1982), одна из первых игр с изометрической графикой

См. также: Категория:Компьютерные игры с изометрической графикой

Примечания

Ссылки

Introduction to 3 Dimensional graphics (англ.). Blueprint project. IDER group, Manufactuing Systems Engineering Centre, University of Hertfordshire. — Пояснения и учебник по рисованию в изометрической перспективе из Хертфорширдского университета.(недоступная ссылка — история) Проверено 29 сентября 2008.
Herbert Glarner. Isometric Projection (англ.) (19 марта 2007). Архивировано из первоисточника 19 февраля 2012. Проверено 29 сентября 2008.
PixelDam (англ.). — A collaborative pixelart community. Архивировано из первоисточника 19 февраля 2012. Проверено 29 сентября 2008.
Tom Gersic. Rendering Isometric Tiles in Blender 3D (англ.). — Учебник с примерами по созданию изометрических плиток в программе Blender 3D. Архивировано из первоисточника 19 февраля 2012. Проверено 29 сентября 2008.

Литература

Богданов В. Н., Малежик И. Ф., Верхола А. П. и др. Справочное руководство по черчению. — М.: Машиностроение, 1989. — С. 864. — ISBN 5-217-00403-7
Фролов С. А. Начертательная геометрия. — 2-е изд., перераб. и доп. — М.: Машиностроение, 1983. — С. 240.

dikc.academic.ru

Прямоугольная изометрическая проекция. Прямоугольная изометрическая проекция

Изометрическая проекция - это... Что такое Изометрическая проекция?

Стандартные изометрические проекции[1]

Прямоугольная (ортогональная) изометрическая проекция

Косоугольная фронтальная изометрическая проекция

Косоугольная горизонтальная изометрическая проекция

Визуализация

Матричные преобразования

Ограничения аксонометрической проекции

Изометрическая проекция в компьютерных играх и пиксельной графике

История изометрических компьютерных игр

Примечания

Ссылки

Литература

ПРЯМОУГОЛЬНАЯ ИЗОМЕТРИЧЕСКАЯ ПРОЕКЦИЯ

Похожие статьи:

Прямоугольная изометрическая проекция

Изометрическая проекция — WiKi

Стандартные изометрические проекции[1]

Прямоугольная (ортогональная) изометрическая проекция

Косоугольная фронтальная изометрическая проекция

Косоугольная горизонтальная изометрическая проекция

Визуализация

Матричные преобразования

Ограничения аксонометрической проекции

Изометрическая проекция в компьютерных играх и пиксельной графике

История изометрических компьютерных игр

Примечания

Ссылки

Литература

Прямоугольная изометрическая проекция.

Прямоугольная изометрическая проекция

Производство Прямоугольная изометрическая проекция просмотров - 463

Читайте также

Изометрическая проекция - это... Что такое Изометрическая проекция?

Стандартные изометрические проекции[1]

Прямоугольная (ортогональная) изометрическая проекция

Косоугольная фронтальная изометрическая проекция

Косоугольная горизонтальная изометрическая проекция

Визуализация

Матричные преобразования

Ограничения аксонометрической проекции

Изометрическая проекция в компьютерных играх и пиксельной графике

История изометрических компьютерных игр

Примечания

Ссылки

Литература

Производство Прямоугольная изометрическая проекция
просмотров - 463