23.Пластичность металлов, влияние на пластичность химического состава, температуры нагрева, схемы напряженного состояния, скорость деформации.

Пластичность—
способность металла принимать под
действием нагрузки новую форму не
разрушаясь.

Пластичность
металлов определяется также при
испытании на растяжение. Это свойство
обнаруживается в том, что под действием
нагрузки образцы разных металлов в
различной степени удлиняются, а их
поперечное сечение уменьшается. Чем
больше способен образец удлиняться, а
его пеперечное сечение сужаться, тем
пластичнее металл образца.

В
условиях обработки металлов давлением
на пластичность влияют многие факторы:
состав и структура деформируемого
металла, характер напряженного состояния
при деформации, неравномерность
деформации, скорость деформации,
температура деформации и др. Изменяя
те или иные факторы, можно изменять
пластичность.

1.Состав
и структура металла.
Пластичность находится в прямой
зависимости от химического состава
материала. С повышением содержания
углерода в стали пластичность падает.
Большое влияние оказывают элементы,
входящие в состав сплава как примеси.
Олово, сурьма, свинец, сера не растворяются
в металле и, располагаясь по границам
зерен, ослабляют связи между ними.
Температура плавления этих элементов
низкая, при нагреве под горячую деформацию
они плавятся, что приводит к потере
пластичности.

2.Влияние
температуры неоднозначно.
Малоуглеродистые
и среднеуглеродистые стали,
с повышением температуры, становятся
более пластичными (1).
Высоколегированные стали имеют большую
пластичность в холодном состоянии (2).
Для шарикоподшипниковых
сталей
пластичность почти не зависит от
температуры (3).
Отдельные сплавы могут иметь интервал
повышенной пластичности (4).
Техническое
железо
в интервале 800…1000⁰
С
характеризуется понижением пластических
свойств (5).
При температурах, близких к температуре
плавления пластичность резко снижается
из-за возможного перегрева
и пережога.

3.Характер
напряженного состояния.
Один и тот же материал проявляет
различную пластичность при изменении
схемы напряженного состояния. Схема
всестороннего сжатия является наиболее
благоприятной для проявления пластических
свойств, так как при этом затрудняется
межзеренная деформация и вся деформация
протекает за счет внутризеренной.
Появление в схеме растягивающих
напряжений снижает пластичность. Самая
низкая пластичность наблюдается при
схеме всестороннего растяжения.

4.Скорость
деформации.
С повышением скорости деформации в
условиях горячей деформации пластичность
снижается. Имеющаяся неравномерность
деформации вызывает дополнительные
напряжения, которые снимаются только
в том случае, если скорость разупрочняющих
процессов не меньше скорости деформации.

Пластичность
зависит от структурного состояния
металла,
особенно при горячей деформации.
Неоднородность микроструктуры снижает
пластичность. Однофазные сплавы, при
прочих равных условиях, всегда пластичнее,
чем двухфазные. Фазы имеют неодинаковые
механические свойства, и деформация
получается неравномерной. Мелкозернистые
металлы пластичнее крупнозернистых.
Металл слитков менее пластичен, чем
металл прокатанной или кованой заготовки,
так как литая структура имеет резкую
неоднородность зерен, включения и
другие дефекты.

Пластичность металлов

Пластичность
– свойство металла пластически
деформироваться, не разрушаясь под
действием внешних сил. Это одно из
важных механических свойств металла,
которое в сочетании с высокой прочностью
делает его основным конструкционным
материалом. Для определения пластичности
образцы и оборудование не требуются.
Показатели (характеристики) пластичности
– относительные удлинение

(дельта) и
сужение
(кси).

Относительным
удлинением
называется отношение абсолютного
удлинения, т. е. приращение расчетной
длины образца после разрыва,
к его первоначальной расчетной длине,мм, выраженное
в процентах:

%,
(2)

где

– длина
образца после разрыва, мм.

Относительным
сужением
называется отношение абсолютного
сужения, т. е. уменьшение площади
поперечного сечения образца после
разрыва,
к первоначальной площади его поперечного
сечения
мм²,выраженное
в процентах:

%,
(3)

где – площадь
поперечного сечения образца после
разрыва,мм²_.

Твердость
– свойство металла сопротивляться
внедрению в него другого более твердого
тела. Для определения твердости не
требуется изготовления специальных
образцов, испытания проводятся без
разрушения металла.

Твердость
металла определяют прямыми и косвенными
методами: вдавливанием, царапанием,
упругой отдачей, магнитным.

При
прямых методах в металл вдавливают
твердый наконечник (индентор) различной
формы (шарик, конус, пирамида) из закаленной
стали, алмаза или твердого сплава. После
снятия нагрузки на индентор в металле
остается отпечаток, который и характеризует
твердость.

Метод
Бринелля.
В плоскую поверхность металла вдавливается
стальной закаленный шарик диаметра 10
мм (рисунок 2). После снятия нагрузки в
металле остается отпечаток (лунка).
Диаметр отпечатка d измеряют специальным
микроскопом с точностью 0,05 мм. На практике
пользуются специальной таблицей, в
которой диаметру отпечатка d соответствует
определенное число твердости НВ.

Диаметр
шарика D
и нагрузку P
устанавливают в зависимости от твердости
и толщины испытуемого металла. Например,
для стали и чугуна нагрузка Р
= 3000 кг; D
= 10 мм. Твердость технически чистого
железа по Бринеллю равна 80 – 90 единиц.

а
б

а
– по Бринеллю; б – по Роквеллу

Рисунок
2 — Схема испытания твердости

Метод
Бринелля не рекомендуется применять
для металлов с твердостью более НВ 450,
так как шарик может деформироваться и
в результате получится искаженный
результат. Этот метод используется в
основном для измерения твердости
заготовок и полуфабрикатов из
неупрочненного металла.

Метод
Роквелла.
Твердость определяют по глубине
отпечатка. Индентором служит стальной
закаленный шарик диаметра 1,58 мм для
мягких металлов или алмазный конус с
углом при вершине 120º
для твердых и сверхтвердых (более HRC
70) металлов (рисунок 2, б).

Шарик
и конус вдавливаются в металл под
действием двух нагрузок – предварительной
и основной. Общая нагрузка равна их
сумме. Предварительная нагрузка
принимается одинаковой для всех металлов
(10 кг). Перед началом испытания большая
стрелка твердомера выставляется на «0»
шкалы индикатора, и затем включается
основная нагрузка – большая стрелка
перемещается по шкале индикатора и
показывает значение твердости.

При
вдавливании стального шарика нагрузка
составляет 100 кг, отсчет твердости
производится по внутренней (красной)
шкале индикатора, твердость обозначают
НRВ. При вдавливании алмазного конуса
твердость определяется по показанию
стрелки по внешней (черной) шкале
индикатора. Для твердых металлов основная
нагрузка составляет 150 кг. Это основной
метод измерения твердости закаленных
сталей. Обозначение твердости – НRC.

Для
очень твердых, а также тонких материалов
нагрузка принимается равной 60 кг.
Обозначение твердости – НRА.

Метод
определения твердости по Роквеллу
позволяет испытывать мягкие и твердые
металлы, при этом отпечатки от шарика
или конуса очень малы, поэтому этим
методом можно измерять твердость и
готовых деталей. Поверхность для
испытания должна быть шлифованной.
Измерения выполняются быстро (в течение
30 – 60 с), не требуется никаких вычислений,
так как значение твердости снимается
по шкале индикатора твердомера.

Метод
Виккерса.
В испытуемую поверхность (шлифованную
или полированную) вдавливается
четырехгранная алмазная пирамида под
нагрузкой 5, 10, 20, 30, 50 или 100 кг. В металле
остается квадратный отпечаток. Специальным
микроскопом твердомера измеряют
диагональ отпечатка (рисунок 3).

Зная
нагрузку на пирамиду и диагональ
отпечатка, по таблицам определяют
твердость металла НV.

Метод
универсальный.
Его можно использовать для определения
твердости деталей малой толщины и тонких
поверхностных слоев большой твердости
(после азотирования, нитроциментации
и т. п.).Чем тоньше металл, тем меньше
должна быть нагрузка на пирамиду, однако
при большой нагрузке результат получается
точнее.

Пластичность металлов

Введение

Считается, что исследование пластичности металлов началось в 1864 году с открытия Трески.
публикация его критерия максимального напряжения сдвига для текучести. С тех пор он
расширен, чтобы включить эффекты анизотропии, зависимости скорости и микроскопического
эффекты, связанные с зернами, дислокациями и плоскостями скольжения атомов.

На этой странице сначала будут рассмотрены основные механизмы пластических деформаций,
которые происходят на атомном уровне. Затем он перейдет к макромасштабным моделям
пластичность. Макромасштабные подходы рассматривают металлы как изотропные континуумы ​​вниз.
до наименьших возможных масштабов. Он начинается с одномерных приложений, которые
кажутся смехотворно простыми, но позволяют понять фундаментальные принципы.
представил. Затем он переходит к 3-D приложениям.

Основные механизмы

Ключевым фундаментальным механизмом пластичности металлов является движение
атомов вдоль плоскостей атомного скольжения. Например, на двумерном рисунке ниже
кружки представляют атомы, упакованные вместе в металле. Металл
подвергается макроскопическому напряжению сдвига, как показано на рисунке. Как это обычно бывает,
внешняя нагрузка не совпадает с плоскостями скольжения.
Это делает механизмы деформации в микроскопическом масштабе весьма
сложный.

В этом двумерном примере есть три основные плоскости скольжения. (Есть еще много
в реальном трехмерном мире.) Они обозначены на рисунке ниже. Каждая плоскость скольжения
имеет единичный вектор нормали \({\bf n}_i\) и вектор направления скольжения,
\({\bf s}_i\).

Скольжение не происходит на плоскости скольжения, если разрешенное напряжение сдвига на
плоскость скольжения превышает критическое разрешенное касательное напряжение материала.
Разрешенное напряжение сдвига рассчитывается по формуле

\[
\tau_\text{разрешено} = \sigma_{ij} s_i n_j
\]

В этом примере должно быть ясно, что по мере увеличения внешней поперечной нагрузки
наиболее быстро будет возрастать разрешенное касательное напряжение на плоскости скольжения № 1 и
сначала срабатывает проскальзывание на этом самолете, задолго до (если вообще) других систем проскальзывания
стать активным.

Конечным результатом является то, что все плоскости скольжения, параллельные #1, начинают сдвигаться, создавая

Обычно это также сопровождается вращением плоскостей скольжения.
Должно быть ясно, что процесс не изменяет объем материала.
Вот почему пластичность несжимаема (что несомненно установлено в
тесты, проведенные Бриджменом в 1947 и 1952). Кроме того, когда атомы скользят,
дислокации (глюки в атомных стеках) растут в числе и повышают
критическое разрешенное напряжение сдвига, необходимое для поддержания дальнейшей пластической деформации.
Это объясняет постепенное увеличение напряжения при продолжении пластической деформации.

Все это только для одного зерна. Это делает его очень анизотропным, потому что
любой приложенный сдвиг, который совпадает с плоскостью скольжения, приведет к более низкому пределу текучести
чем прикладной сдвиг, который не выравнивается. Но если вы не лопатка турбины, то
металл на самом деле состоит из миллионов или миллиардов беспорядочно ориентированных зерен. e}\). Это приписывается Ли (19п}
\]

Обратите внимание, что, как и в случае с полярными разложениями, матрицы считываются из
справа налево. Таким образом, в этом случае предполагается, что пластическая деформация принимает
первое место, затем упругие деформации.

Одномерная пластичность металла

Сложность микромасштабных описаний пластичности металлов,
поликристаллический пластик , поэтому для 99,99% применений,
используются макромасштабные теории пластичности. Они очень эмпиричны.
Они основаны исключительно на наблюдаемом поведении на макроуровне.

Этот процесс начинается с простых одноосных кривых напряжения-деформации, как показано ниже.

На графике показано так называемое изотропное и кинематическое упрочнение, которое происходит
в металлах. Кинематический аспект – это анизотропная часть, отвечающая за
для центра поверхности текучести, дрейфующей от нуля. Это
иногда называемый эффектом Баушингера в честь исследователя, который
впервые определил его в 1881 году. Изотропный аспект симметричен независимо от
направление загрузки.
9м
\]

Только имейте в виду, что пластиковая часть полностью эмпирическая. Это только
кривая подходит только для одномерных приложений, где деформации
относительно небольшой, потому что один показатель степени m не может соответствовать данным более
большие диапазоны деформации.

Трехмерная пластичность металла

Ситуация значительно сложнее в 3D. В таком случае,
текучесть диктуется напряжением фон Мизеса. Напомним, что это
круг, как на следующем эскизе.

Обратите внимание, что приведенный выше рисунок относится к чисто изотропному случаю. кинематический
затвердевание изображается кружком, удаляющимся от начала координат.
Поскольку это происходит в пространстве напряжений, центр окружности
описывается бесследным тензором напряжений \(\alpha_{ij}\), называемым обратным напряжением
тензорная или кинематическая переменная упрочнения.

пластичность_(физика)

В физике и материаловедении пластичность — это свойство материала претерпевать необратимое изменение формы в ответ на приложенную силу. Например, твердый кусок металла или пластика, сгибаемый или растираемый в новую форму, проявляет пластичность, поскольку в самом материале происходят постоянные изменения. Напротив, постоянная складка на листе бумаги или изменение формы влажной глины происходит из-за перегруппировки отдельных волокон или частиц. В технике переход от упругого поведения к пластическому называется пределом текучести.

Дополнительные рекомендуемые знания

Пояснение

Для многих пластичных металлов растягивающая нагрузка, приложенная к образцу, приводит к тому, что он ведет себя упруго. Каждое увеличение нагрузки сопровождается пропорциональным увеличением растяжения, и когда нагрузка снимается, деталь возвращается точно к своему первоначальному размеру. Однако, как только нагрузка превышает некоторый порог (предел текучести), удлинение увеличивается быстрее, чем в упругой области, и когда нагрузка снимается, некоторое удлинение остается. Общий график, отображающий это поведение, приведен ниже.

Пластичность – это свойство материалов подвергаться большой деформации без разрушения. Это встречается в большинстве металлов и в целом является хорошим описанием большого класса материалов.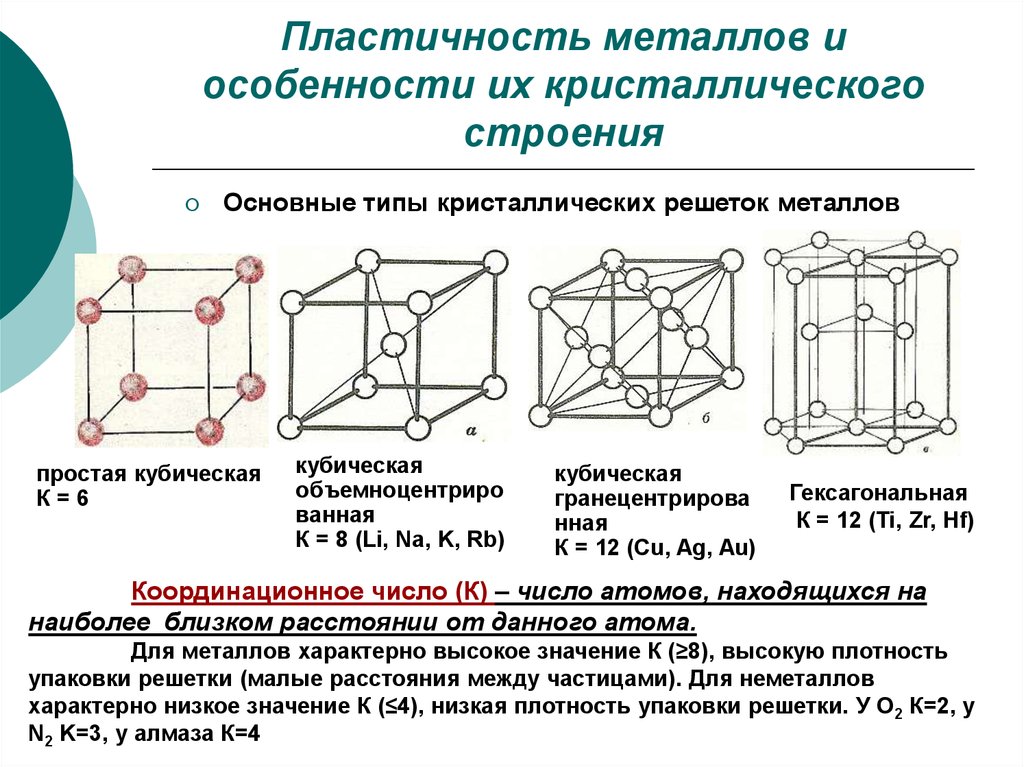 Совершенная пластичность — это свойство материалов подвергаться большим сдвиговым деформациям без какого-либо увеличения (сдвигового) напряжения. Пластмассовые материалы, которые не являются идеально пластичными, являются вязкопластичными.

Микроскопически пластичность металлов является следствием дислокаций.

Математические описания пластичности

Теория деформации

Существует несколько математических описаний пластичности. Одним из них является теория деформации (см., например, закон Гука), где тензор напряжений (порядка d в ​​d измерениях) является функцией тензора деформации. Хотя это описание является точным, когда небольшая часть вещества подвергается возрастающей нагрузке (например, деформации), эта теория не может объяснить необратимость.

На изображении выше представлена ​​составляющая напряжения сдвига по отношению к составляющей деформации сдвига при возрастающей деформационной нагрузке.

Пластичные материалы могут выдерживать большие пластические деформации без разрушения. Однако даже пластичные металлы разрушаются, когда деформация становится достаточно большой — это происходит в результате наклепа материала, что делает его хрупким. Термическая обработка, такая как отжиг, может восстановить пластичность обрабатываемой детали, чтобы можно было продолжить формование.

Теория пластичности течения

В 1934 году Эгон Орован, Майкл Поланьи и Джеффри Инграм Тейлор примерно одновременно поняли, что пластическую деформацию пластичных материалов можно объяснить с точки зрения теории дислокаций.
Более правильная математическая теория пластичности, теория пластичности течения, использует набор нелинейных, неинтегрируемых уравнений для описания набора изменений деформации и напряжения по отношению к предыдущему состоянию и небольшому увеличению деформации.

Эластичный и пластический отказ

Если напряжение превышает критическое значение, как было сказано выше, материал подвергается пластической, или необратимой, деформации. Это критическое напряжение может быть растягивающим или сжимающим.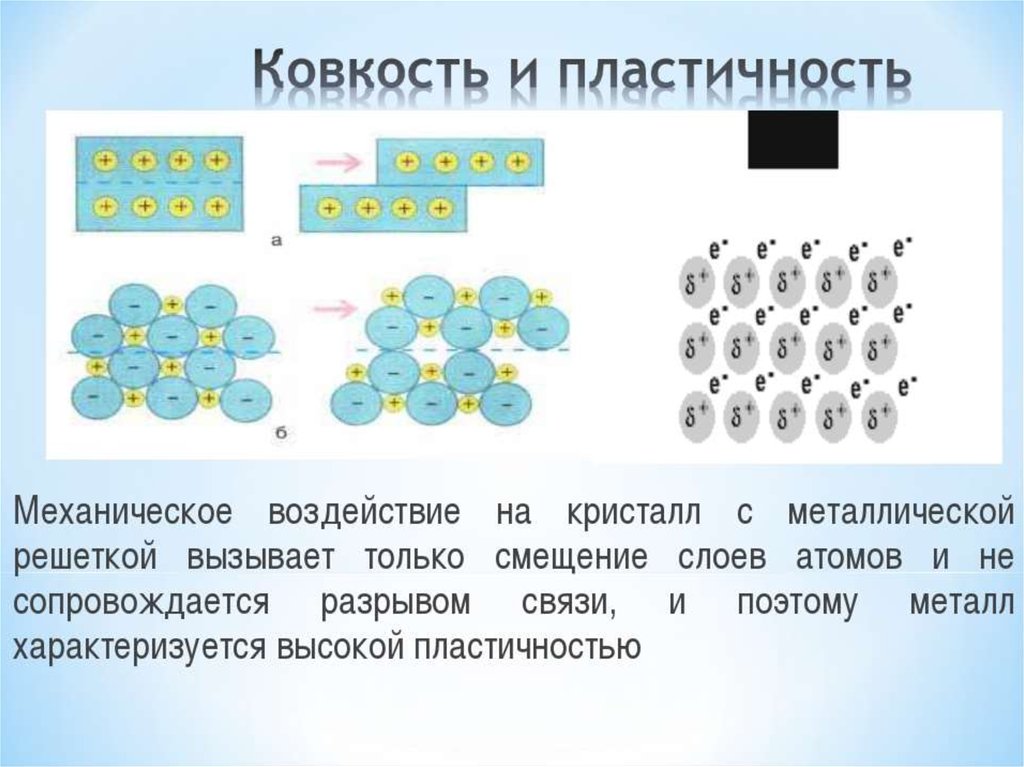

Критерий Трески

Этот критерий основан на представлении о том, что разрушение материала происходит при сдвиге, что является относительно хорошим предположением при рассмотрении металлов. Учитывая основное напряженное состояние, мы можем использовать круг Мора, чтобы определить максимальные напряжения сдвига, которые испытает наш материал, и сделать вывод, что материал выйдет из строя, если:

σ ₁ — σ ₃ ≥ σ ₀

Где σ ₁ — максимальное нормальное напряжение, σ ₃ — минимальное нормальное напряжение, при котором 96 8 σ0 90 материал разрушается при одноосном нагружении. Можно построить поверхность текучести, которая обеспечивает визуальное представление этой концепции. Внутри поверхности текучести деформация упругая. Вне поверхности деформация носит пластический характер. См. Анри Треска.

Критерий фон Мизеса

Этот критерий основан на критерии Трески, но принимает во внимание допущение, что гидростатические напряжения не способствуют разрушению материала. Фон Мизес находит эффективное напряжение при одноосной нагрузке, вычитая гидростатические напряжения, и утверждает, что все действующие напряжения, превышающие то, которое вызывает разрушение материала при одноосной нагрузке, приведут к пластической деформации.

σ _{эффективный} ² = 1/2 ((σ ₁₁ – σ ₂₂ )² + (σ ₂₂ – σ ₃₃ )² + (σ ₁₁ – σ ₃₃ )²) + 3 (σ ₁₂ ² + σ ₁₃ ² + σ 2

²) 6 σ 2

Опять же, визуальное представление поверхности текучести может быть построено с использованием приведенного выше уравнения, которое принимает форму эллипса. Внутри поверхности материалы подвергаются упругой деформации. Вне поверхности они подвергаются пластической деформации. См. стресс фон Мизеса

Атомные механизмы

Системы скольжения

Кристаллические материалы содержат однородные плоскости атомов, организованные в дальнем порядке. Самолеты могут проскальзывать друг мимо друга в тесном направлении, как показано на вики-странице систем скольжения. Результатом является постоянное изменение формы внутри кристалла и пластическая деформация. Наличие дислокаций увеличивает вероятность скольжения самолетов.

Срезная лента

Наличие других дефектов внутри кристалла может запутывать дислокации или иным образом препятствовать их скольжению. Когда это происходит, пластичность локализуется в определенных областях материала. Для кристаллов эти области локализованной пластичности называются полосами сдвига.

Безумие

В аморфных материалах обсуждение «дислокаций» неприменимо, так как во всем материале отсутствует дальний порядок. Эти материалы все еще могут подвергаться пластической деформации. Поскольку аморфные материалы, такие как полимеры, плохо упорядочены, они содержат большое количество свободного объема или неиспользуемого пространства. Натяжение этих материалов при растяжении открывает эти области и может придать материалам нечеткий вид. Эта мутность является результатом образования трещин , когда в материале образуются волокна в областях с высоким гидростатическим напряжением. Материал может превратиться из упорядоченного вида в «сумасшедший» рисунок деформации и растяжек.

Мартенситные материалы

Некоторые материалы, особенно склонные к мартенситным превращениям, деформируются способами, которые плохо описываются классическими теориями пластичности и упругости. Одним из самых известных примеров этого является нитинол, который проявляет псевдоэластичность: деформации, которые обратимы в контексте механического проектирования, но необратимы с точки зрения термодинамики.

Ячеистые материалы

Эти материалы пластически деформируются, когда изгибающий момент превышает полностью пластический момент. Это относится к пенам с открытыми порами, где изгибающий момент действует на стенки ячеек. Пенопласты могут быть изготовлены из любого материала с пластическим пределом текучести, включая жесткие полимеры и металлы. Этот метод моделирования пены в виде балок допустим только в том случае, если отношение плотности пены к плотности материала меньше 0,3.