Содержание
Прекционное черчение — Стр 3
19
г) Соединяем полученные на П1 проекции точек с учетом видимости, используя порядок движения по плоскостям выреза. На плоскости П1 (вид сверху) все грани пирамиды видимы, поэтому и линии пересечения будут видимы. Движение осуществляем следующим образом: от точки 1 к точке 3 (прямая 1131), от точки 3 к точке 2 (прямая 3121), далее к точке 4 (прямая 2141), затем к точке 5 (прямая 4151) и, наконец, к точке 1 (прямая 5111). На задней грани получим прямые 11$21$ , 21$41$ и 11$41$ .
3.Строим профильные проекции полученных прямых, для этого сначала строим профильные проекции точек 1, 1′, 2, 2′, 3, 4, 4′, 5. Соединяем полученные проекции точек прямыми с учетом видимости, используя порядок движения по
плоскостям выреза: от точки 1 к точке 3 (1333 видима), к точке 2 по невидимой
грани (3323 невидима), к точке 4 (2343 невидима), к точке 5 (4353 невидима), к точке 1 (1353 видима). Проекции 1$32$3 , 2$34$3 и 1$34$3 совпадают с проекцией грани.
4.Строим проекции линий пересечения плоскостей призматического отверстия: 11′ – проекция линии пересечения плоскостей α и γ, 22′ – проекция линии пересечения плоскостей α и β, 44′ – проекция линии пересечения плоскостей β и γ. Эти прямые находятся внутри пирамиды, поэтому на П1 и П3 они невидимы.
5.Удаляем те участки пирамиды, которые оказались вырезанными отверстием; это часть ребра между точками 3 и 5, а также части граней, заключенные между плоскостями выреза. Часть прямой 2343 становится видимой.
6.Обводим проекции пирамиды и полученные линии выреза.
2.2. Поверхности вращения
Поверхности, которые образуются вращением образующей вокруг неподвижной оси, называются поверхностями вращения (рис. 15 а).
Рис. 15. Образование поверхности вращения
Линейчатые поверхности вращения – те поверхности, образующая которых прямая (цилиндрическая, коническая поверхности вращения).
20
Нелинейчатые поверхности вращения – те поверхности, образующая которых кривая линия (сфера, тор).
Каждая точка образующей при вращении вокруг оси описывает окружность в плоскости, перпендикулярной оси вращения (рис. 15 а). Эта окружность называется параллелью. Параллель наибольшего диаметра называется экватором, наименьшего диаметра – горлом (рис. 15 б). Если через ось вращения i провести плоскость, то она пересечет поверхность вращения по образующей – меридиану. Главные меридианы поверхности – фронтальный (в плоскости, параллельной фронтальной плоскости проекций) и профильный (в плоскости, параллельной профильной плоскости проекций) (рис. 15 б). Меридианы и параллели часто используются при построении комплексных чертежей.
2.2.1. Цилиндр
Цилиндрическая поверхность вращения образуется вращением прямолинейной образующей вокруг оси, параллельной образующей (рис. 16 а и б).
Рис. 16. Образование цилиндрической поверхности и цилиндра
Цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью и двумя перпендикулярными к оси вращения плоскостями (рис. 16 в). Отсеченная часть цилиндрической поверхности – это боковая поверхность цилиндра, а круги, расположенные в секущих плоскостях, – основания цилиндра. Полученное таким обра-
16 в). Отсеченная часть цилиндрической поверхности – это боковая поверхность цилиндра, а круги, расположенные в секущих плоскостях, – основания цилиндра. Полученное таким обра-
зом тело называется прямым круго- Рис. 17. Прямой круговой цилиндр
вым цилиндром (рис. 17).
21
Условие принадлежности точки поверхности цилиндра
Если точка А принадлежит поверхности цилиндра (рис. 18), то она принадлежит:
!» образующей lА, параллельной оси вращения i; !» окружности nA в плоскости, перпендикуляр-
ной оси вращения.
Следовательно, точку на поверхности цилиндра можно построить по двум простым линиям: либо образующей (прямой), либо окружности, центр которой лежит на оси вращения.
Рис. 18. Принадлежность точки поверхности цилиндра
Рассмотрим изображения цилиндра вращения на комплексном чертеже
(рис. 19).
Рис. 19. Комплексный чертеж прямого кругового цилиндра
22
Чтение комплексного чертежа цилиндра
1. Ось вращения i перпендикулярна горизонтальной плоскости проекций и на П1 изобразится в виде точки (центр окружности основания).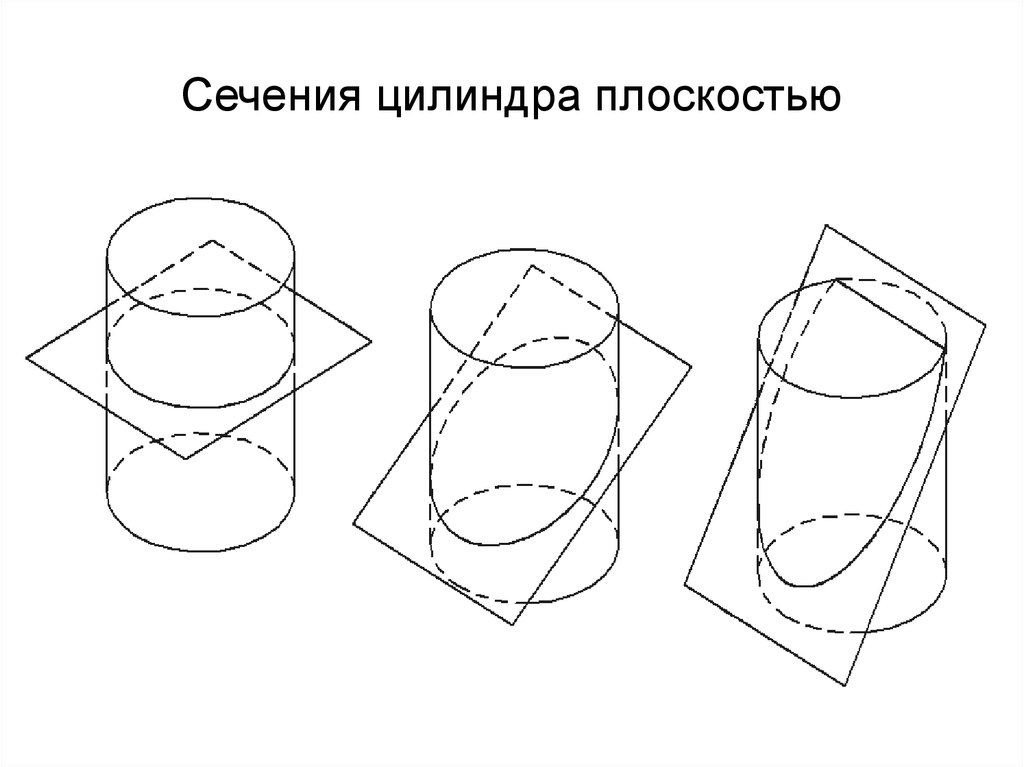
2.Основания цилиндра – круги, расположенные в горизонтальных плоскостях уровня, поэтому на П1 они изобразятся в виде окружностей в натуральную величину,
ана П2 – в виде отрезков, длина которых равна диаметру окружностей основания.
3.Образующие перпендикулярны П1.
4.Боковая поверхность цилиндра занимает проецирующее положение по
отношению к плоскости П1 и спроецируется в окружность, совпадающую с проекцией оснований.
5.Горизонтальный очерк цилиндра – окружность, обладающая собирательным свойством.
6.Фронтальный очерк – прямоугольник, образованный проекциями оснований в виде отрезков и фронтальными очерковыми образующими (прямыми) 11′ и 33′ – фронтальными меридианами.
7.Видимость поверхности. На плоскости П1 видимо верхнее основание цилиндра. При проецировании на П2 граница видимости проходит через фронтальный меридиан 11′ и 33′, поэтому видимой на П2 является ближняя к наблюдателю половина боковой поверхности цилиндра.
Построение профильной проекции цилиндра по двум известным
1. Построение профильной проекции оси вращения i3.
Построение профильной проекции оси вращения i3.
2.Проецирование окружностей оснований по горизонтальным линиям связи. Центры окружностей основания лежат на оси вращения, окружности оснований изобразятся в виде отрезков, длина которых равна диаметрам окружностей оснований.
3.Через крайние точки окружностей оснований проходят профильные очерковые образующие (прямые).
4.Профильный очерк – прямоугольник, образованный проекциями оснований
ввиде отрезков и крайними образующими (профильными меридианами) 22′ и 44′.
5.Видимой на П3 является левая половина боковой поверхности цилиндра.
Построение точки на поверхности цилиндра
1. Пусть точка А задана своей фронтальной проекцией А2. Для построения горизонтальной проекции точки А1 не требуется проведения вспомогательных линий, так как цилиндрическая поверхность проецирующая на П1. Следовательно, А1 находим на окружности, являющейся горизонтальным очерком цилиндра. Вертикальная линия связи пересекает эту окружность в двух точках. Выбираем ту из них, которая ближе к наблюдателю, так как А2 задана видимой. А3 строим по двум известным проекциям. Определяем видимость А3. При взгляде на цилиндр слева точка А лежит на ближней к наблюдателю половине цилиндра, значит А3 видима.
Выбираем ту из них, которая ближе к наблюдателю, так как А2 задана видимой. А3 строим по двум известным проекциям. Определяем видимость А3. При взгляде на цилиндр слева точка А лежит на ближней к наблюдателю половине цилиндра, значит А3 видима.
23
2.Точка В задана фронтальной невидимой проекцией. В1 лежит на дальней от наблюдателя половине цилиндра. В3 строим по двум известным проекциям (ВzВ3 = ВxВ1 = yB). Определим видимость: В3 невидима, так как лежит на дальней от наблюдателя половине цилиндра.
3.Точка С (С2) лежит на самой ближней к наблюдателю образующей 22′.
Находим горизонтальную проекцию С1 (она совпадает с 21) и профильную С3 на профильной очерковой образующей 232$3 .
Линия на цилиндрической поверхности
При пересечении поверхности цилиндра плоскостью можно получить следующие линии:
1) две прямые (образующие), лежащие в плоскости α, параллельной оси вращения цилиндра (рис. 20 а). α || i % α ∩ цилиндр ═ m, m′ – образующие.
Образующая цилиндра – прямая, параллельная оси вращения i. Для ее построения необходимо знать две точки на поверхности цилиндра;
Для ее построения необходимо знать две точки на поверхности цилиндра;
2) окружность, лежащую в плоскости β, перпендикулярной оси вращения цилиндра (рис. 20 б). β & i % β ∩ цилиндр ═ n – окружность.
Окружность на поверхности цилиндра имеет радиус Rn и центр О, лежащий на оси вращения i;
à
Рис. 20. Линии на поверхности цилиндра
24
á
â
Рис. 20. (Продолжение)
3) эллипс, лежащий в плоскости γ, наклоненной к оси вращения цилиндра (рис. 20 в). γ !, &’ i % β ∩ цилиндр ═ l – эллипс.
25
Эллипс – кривая второго порядка, для точного |
| |
построения которой необходимо множество точек. |
| |
Строят количество точек, достаточное для построения |
| |
кривой, а затем обводят кривую с помощью лекал. Из |
| |
этого множества точек выделяют характерные точки |
| |
кривой, без которых точное построение эллипса невоз- |
| |
можно. |
| |
(рис. 21). АВ – большая ось эллипса (AO = OB), СD – | Рис. 21. Эллипс | |
малая ось эллипса (CO = OD), AB & CD. | ||
| ||
Пример построения линии на цилиндре | ||
| Дано: Φ – цилиндр, бо- | |
| ковая поверх- | |
| ность которого | |
| занимает проеци- | |
| рующее положе- | |
| ние к П1 | |
| ————————— | |
| l (l2) – ? | |
| Анализ условия (рис. | |
| Линия l лежит в | |
| плоскости γ, наклонен- | |
| ной к оси вращения ци- | |
| линдра. l – эллипс. | |
| l2 – известна (γ & П2, | |
| γ2 обладает собиратель- | |
| ным свойством). | |
| l1 – известна (Ф & П1, | |
| Ф1 обладает собиратель- | |
| ным свойством). | |
| ————————— | |
Рис. 22. Построение линии на цилиндре | l3 – ? | |
| ||
Порядок решения:
1. Опорные точки: АВ – большая ось эллипса; СD – малая ось эллипса; С и D – точки видимости на П3.
Опорные точки: АВ – большая ось эллипса; СD – малая ось эллипса; С и D – точки видимости на П3.
2. Промежуточные точки строятся по условию принадлежности точки поверхности цилиндра (см. «Построение точки на поверхности цилиндра», стр. 22).
Соединяем полученные точки плавной кривой по лекалам тонкой линией, следя за тем, чтобы проекция эллипса была симметрична относительно большой и малой оси эллипса.
26
3. Видимость эллипса. На П1 эллипс совпадает с проекцией поверхности цилиндра. На П3 видима часть эллипса ближе границы видимости до точек видимости C3 и D3. К точке В3 уходит невидимая часть эллипса.
Пример построения выреза в цилиндре
Рис. 23. Задание для построения выреза в цилиндре
Анализ условия (чтение исходного чертежа) (рис. 23)
Дано: 1. Цилиндр, боковая поверхность которого занимает проецирующее положение по отношению к П1 (собирательное свойство горизонтальной проекции).
2.Сквозное призматическое отверстие, образованное тремя плоскостями, занимающими проецирующее положение по отношению
к П2 (собирательное свойство фронтальной проекции отверстия).
Вывод: горизонтальные и фронтальные проекции линий пересечения известны, необходимо построить их профильные проекции.
Порядок решения:
1. Строим изображение цилиндра (рис. 24) без учета отверстия, пользуясь введенными внутренними координатными осями и линиями проекционной связи.
2. Строим проекции линий пересечения каждой плоскости, ограничивающей отверстие, с цилиндрической поверхностью.
а) Нижняя плоскость отверстия лежит в плоскости α, которая является горизонтальной плоскостью уровня. Плоскость α перпендикулярна оси i и пересекает цилиндрическую поверхность по окружности, горизонтальная проекция которой совпадает с горизонтальным очерком цилиндра. Но в вырез попадает не вся окружность, а две дуги окружности, ограниченные прямыми 11′ и 22′. Поэтому на передней половине цилиндра получаем дугу 12, а на задней половине – дугу 1′2′.
б) Плоскость выреза β параллельна оси вращения цилиндра i, поэтому на цилиндрической поверхности в плоскости β лежат две образующие (прямые), для построения которых необходимы две точки: точки 2 и 3 (на ближ-
27
ней половине цилиндра) и точки 2′ и 3′ (на задней половине цилиндра). Прямые 23 и 2′3′ – проецирующие по отношению к П1.
Прямые 23 и 2′3′ – проецирующие по отношению к П1.
Рис. 24. Построение выреза в цилиндре
в) Плоскость выреза γ располагается под углом к оси вращения цилиндра i, поэтому на цилиндрической поверхности образуется эллипс. Построение эллипса на цилиндрической поверхности рассмотрено на стр. 25.
Опорные точки: АВ – большая ось эллипса; СD – малая ось эллипса;
5 и 6 – точки видимости на П3.
Промежуточные точки строятся из условия принадлежности цилиндрической поверхности.
Эллипс строится полностью, а затем выделяются участки, попадающие в вырез, с учетом видимости.
3.Строим проекции линий пересечения плоскостей призматического отверстия: прямая 11′ – пересечение плоскостей α и γ, прямая 22′ – пересечение плоскостей α и β, прямая 33′ – пересечение плоскостей β и γ. Эти прямые находятся внутри цилиндра, поэтому на П1 и П3 они невидимы.
4.Удаляем те участки цилиндра, которые вырезаны отверстием. Это части
образующих между точками 4, С и точками 4′, D, а также части цилиндра, заключенные между плоскостями выреза. Части прямых 2333 и 2$33$3 до эллипса ничем
Части прямых 2333 и 2$33$3 до эллипса ничем
не закрыты, а значит, видимы на П3.
5. Обводим проекции цилиндра и полученные линии выреза.
28
2.2.2. Конус
Коническая поверхность вращения образуется вращением вокруг оси прямолинейной образующей, пересекающей эту ось (рис. 25 а и б). Точка пересечения образующей с осью вращения называется вершиной конической поверхности.
Рис. 25. Образование конической поверхности и конуса
Конус – геометрическое тело, ограниченное конической поверхностью и плоскостью, перпендикулярной оси вращения (рис. 25 в). Отсеченная часть конической поверхности – это боковая поверхность конуса, а круг, расположенный в секущей плоскости, – основание конуса. Полученное таким образом тело называ-
ется прямым круговым конусом (рис. 26).
Условие принадлежности точки поверхности конуса
Если точка А принадлежит поверхности конуса (рис. 27), то она принадлежит: 1) образующей lA , проходящей через вершину S;
2) окружности nA в плоскости, перпендикулярной оси вращения.
Поэтому точку на поверхности конуса можно построить по двум простым линиям: либо образующей (прямой), либо окружности (Оn # i, Rn).
Рис. 26. Прямой круговой конус | Рис. 27. Принадлежность | |
точки поверхности конуса | ||
|
Приложения
Ботвинников А.Д. § 10 [1] Степакова В. В. § 9-11 [3]
Куб
Ромбокубоктаэдр Преобразование ромбокубооктаэдра в «левый» и «правый» курносые кубы
Ромбоикосододекаэдр
Трансформация из ромбоикосидодекаэдра в плосконосый додекаэдр
Это интересно! pdf Прочитай чертёж pdf Кто автор? pdf Что означают слова pdf Видео «1D-2D-3D-4D — Что это такое?» pdf Лента Мёбиуса
| Многообразие геометрических форм На уроках математики вы уже познакомились с некоторыми геометрическими фигурами. Если все точки фигуры лежат в одной плоскости, фигуру называют плоской: треугольник, квадрат и др. Совокупность точек, расположенных в пространстве, образует пространственную фигуру: куб, цилиндр и др. Фигуры в пространстве называют геометрическими телами. Предметы, которые нас окружают, детали машин имеют, как правило, сложную реальную геометрическую форму. Однако, присмотревшись к ним внимательно, можно заметить, что некоторые из них состоят из одного или нескольких простых геометрических тел или их видоизмененных частей. Такими геометрическими телами, образующими форму предметов, являются призмы, пирамиды, цилиндры, конусы, шары и др. (рис. 1) Рис. 1. Геометрические тела По форме простые геометрические тела делятся на многогранники и тела вращения. Многогранники – геометрические тела, поверхность которых состоит из плоских многоугольников. Это куб, призма, параллелепипед, пирамида и др. Тела вращения – геометрические тела, поверхность которых описывается какой-либо прямой или кривой (образующей) при её вращении вокруг неподвижной оси (например, конус, цилиндр, шар и т. п.). Форма каждого геометрического тела имеет свои характерные признаки. По ним мы отличаем призму от цилиндра, пирамиду от конуса и т. п. Эти признаки используются и при построении чертежей геометрических тел или состоящих из них предметов и деталей. Однако прежде чем выполнять такие чертежи, выясним, какие правила положены в основу способов их построения. Поскольку форма большинства предметов представляет собой сочетание различных геометрических тел или их частей, для построения чертежей этих предметов необходимо знать, как изображается каждое геометрическое тело. Изображение многогранников Рассмотрим построение прямоугольных проекций призмы. Для примера возьмем треугольную призму (рис. 2) и шестиугольную призму (рис. 3). Их основания, параллельные горизонтальной плоскости проекций, изображаются на ней в натуральную величину, а на фронтальной и профильной плоскостях — отрезками прямых. Боковые грани изображаются без искажения на тех плоскостях проекций, которым они параллельны, и в виде отрезков прямых — на тех, которым перпендикулярны. Грани, наклонные к плоскостям, изображаются на них искаженными. Рис. 2. Треугольная призма Рис. Размеры призм определяются их высотами и размерами фигур основания. Штрихпунктирными линиями на чертеже изображаются оси симметрии. Рассмотрим, как изображают на чертеже правильную четырехугольную пирамиду (рис. 4). Основание пирамиды проецируется на горизонтальную плоскость проекций в натуральную величину. На нём диагоналями изображаются проекции боковых ребер, идущих от вершин основания к вершине пирамиды. Рис. 4. Четырехугольная пирамида Фронтальная и профильная проекции пирамиды — равнобедренные треугольники. Размеры пирамиды определяются длиной b двух сторон ее основания и высотой h. Изображение тел вращения Если круги, лежащие в основаниях цилиндра (рис. 5) и конуса 6), расположены параллельно горизонтальной плоскости проекций, их проекции на эту плоскость будут также кругами.
Рис. 6. Конус Фронтальная и профильная проекции цилиндра в данном случае – прямоугольники, а конуса – равнобедренные треугольники. На всех проекциях следует наносить оси симметрии, с проведения которых и начинают выполнение чертежей цилиндра и конуса. Фронтальная и профильная проекции цилиндра одинаковы. То же можно сказать о проекциях конуса. Поэтому в данном случае профильные проекции на чертеже лишние. Кроме того, благодаря знаку диаметра Ø можно представить форму цилиндра и конуса даже по одной проекции (рис. 7, a и б). Отсюда следует, что в подобных случаях нет необходимости в трех проекциях. Размеры цилиндра и конуса определяются их высотой h и диаметром основания d. Рис. 7. Чертежи цилиндра, конуса и шара Все проекции шара – круги, диаметр которых равен диаметру шара. На каждой проекции проводят центровые линии. Благодаря знаку Ø, шар можно изображать в одной проекции (рис. 7, в). Но если по чертежу трудно отличить сферу от других поверхностей, то на чертеже добавляют слово «сфера», например: «Сфера Ø40». Анализ геометрической формы Вы знаете, что форма большинства предметов представляет собой сочетание различных геометрических тел или их частей. Следовательно, для чтения и выполнения чертежей нужно знать, как они изображаются. Форма каждого геометрического тела имеет свои характерные признаки. В основе формы деталей машин и механизмов также находятся геометрические тела. Чтобы понять по чертежу форму сложного предмета, его мысленно разделяют на части, представляющие собой геометрические тела, т. е. анализируют форму (рис. 8). Затем мысленно объединив эти части, воссоздают общую форму предмета. Рис. 8. Кофейник и его элементы Геометрической формой называется внешний облик предмета, характеризующийся совокупностью его геометрических свойств. Предметы бывают простой и сложной формы. К предметам простой формы относятся те, которые представляют собой геометрические тела: цилиндр, конус, шар, призма, пирамида (рис. 9, а). К предметам сложной (составной) формы относятся такие, которые образованы сочетанием различных геометрических тел (рис. 9, б). Рис. 9. Предметы простой (а) и сложной (б) формы Основные геометрические тела можно выявить в любой детали или предмете. Так, на рисунке 10, а в прямоугольной проекции изображена деталь, называемая валиком (от слова «вал»). В ней можно выделить такие геометрические тела, как усеченный конус 1, цилиндр 2, параллелепипед 3 и еще один цилиндр, большего диаметра – 4 (рис. 10, б). Рис. 10. Анализ геометрической формы детали Чтобы представить по чертежу общую форму любой детали, необходимо выявить форму всех ее элементов. Ещё проанализируем форму детали (рис. 11), состоящей из трех геометрических тел: конусов (прямого кругового и усеченного) и цилиндра. Рис. 11. Анализ геометрической формы детали «Конус» на основе расчленения ее на геометрические тела: 1 – конус; 2 – усеченный конус; 3 – цилиндр Все части, составляющие форму рассматриваемого изделия, расположены на одной оси (т. е. соосны). К основанию конуса примыкает равновеликое основание усеченного конуса. Другое основание усеченного конуса совмещается с основанием цилиндра, диаметр которого меньше диаметра конуса. Попробуйте выполнить чертеж детали, представленной на рисунке 12. Рис. 12. Геометрическая разборка формы детали
| Практические задания, тесты и домашние работы Графическая работа
Вопросы для повторения
Тест
Домашняя работа
Черчение с увлечением! pdf Третий лишний pdf Отгадай форму pdf Согни бумагу по чертежу pdf Крыша дома pdf Чайники pdf В чём отличие? pdf Изобрази пробку pdf Модели из проволоки pdf Эвристическая задача
|
табурет средней высоты разделяет сверхмощный газовый баллон замены пневматический 8″ ход
5
Просто работает
Опубликовано TaT 9th Jul 2020
Прибыл быстро.
 Немного нервное биение по моему нынешнему стулу, чтобы сместить старый, и мне пришлось искать сторонние инструкции по этому процессу, но в целом довольно просто. Абсолютно твердый.
Немного нервное биение по моему нынешнему стулу, чтобы сместить старый, и мне пришлось искать сторонние инструкции по этому процессу, но в целом довольно просто. Абсолютно твердый.5
Превосходный и сверхмощный
Опубликовано Роуз 8th Mar 2018
Мне нужно было увеличить высоту новых офисных стульев, а табурет для черчения GC-8 Запчасти для тяжелых условий эксплуатации Пневматический газовый баллон 8 дюймов Ход идеально подходит, очень прочный и очень простой в установке
5
Легко заменить!
Опубликовано Неизвестный 31 января 2018 г.

Он отлично подходил для того, чтобы починить мое прогибающееся кресло и в то же время поднять его, чтобы он лучше подходил для домашнего офиса. У меня был короткий стул и высокая офисная стойка. Я использовал этот продукт, чтобы исправить оба! Легко исправить! Я использовал трубный ключ, чтобы снять старый с кронштейна на дне сиденья. Стучать не получается. Молоток позаботился об удалении нижнего конца с роликами. Лучше купить новый стул!!
5
Деталь высокого качества
Опубликовано ДЖОН ЛОМНИЦКИ 2 июня 2017 г.
Это именно то, что мы искали. Вместо того, чтобы заменить наш стул, это здорово, я сейчас сижу в кресле, и это действительно немного дает, когда я сажусь и восстанавливаюсь — действительно приятно — отличный продукт и немного выше — мы более высокие люди
5
Отличный продукт, цена и обслуживание
Опубликовано Офис-менеджером 10 октября 2016 г.

Нужен новый газовый баллон для нашего офисного стула, и после некоторых исследований мы выбрали echairparts.com. Я не был уверен, какая именно часть мне нужна, написал по электронной почте представителю службы поддержки и получил быстрый ответ на все мои технические вопросы, которые мне нужны для совершения осознанной покупки. Деталь прибыла через 2 дня и была точной подгонкой и заменой!! Эта компания стала нашим постоянным поставщиком запчастей. У них отличная техподдержка!
Как рисовать цилиндры из жизни
Мы получили следующий вопрос от нашего ученика:
» Как найти точку схода (или горизонтальную линию), чтобы правильно нарисовать цилиндр? »
Ответ от Владимир Лондон, репетитор Академии натурного рисунка
Когда вы рисуете с натуры, линия горизонта всегда будет на уровне ваших глаз. Не нужно гадать. Все объекты и элементы над этой линией будут видны снизу; и мы видим сверху все предметы, находящиеся ниже линии горизонта.
Все объекты и элементы над этой линией будут видны снизу; и мы видим сверху все предметы, находящиеся ниже линии горизонта.
Горизонтально расположенные круги в перспективе выглядят как овалы. Однако, когда круг находится на уровне горизонта, он воспринимается как прямая линия. Точка схода стоячего цилиндра будет лежать на линии горизонта. Поскольку стоящий цилиндр можно изобразить в одноточечной перспективе, эта точка схода будет там, где горизонт пересекает вертикальную ось симметрии цилиндра.
Эта точка не нужна для рисования цилиндра. Расположение горизонта и пропорции цилиндра, которые вы измеряете с натуры, достаточны для изображения реалистично выглядящего цилиндрического объекта.
Точку схода можно использовать, если по какой-то причине вы хотите нарисовать прямоугольный параллелепипед, содержащий цилиндр. Это помогает рисовать более сложные архитектурные конструкции, такие как купола зданий, классические капители колонн или урны с кубовидными постаментами.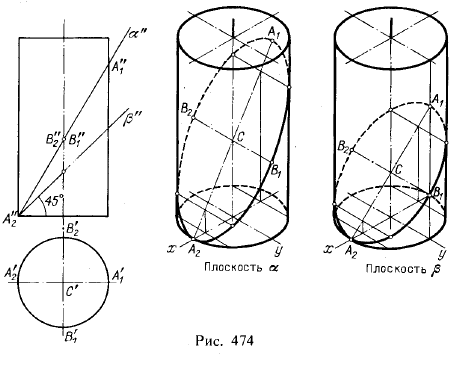
Возвращаясь к вопросу «Как правильно нарисовать цилиндр» . Есть много способов рисования цилиндров. Я дам вам метод, который я использую.
Рисуя стоячий цилиндр с натуры, первый вопрос, который вам нужно решить, — это высота и ширина цилиндра, путем измерения основной пропорции цилиндра — отношения ширины к высоте. Вы можете использовать карандаш, чтобы измерить эту пропорцию или сделать это на глаз. Есть видео Академии рисования, где я показываю, как измерять карандашом.
- Итак, первый шаг — найти основную пропорцию «А-В» и отметить ее на бумаге.
- Следующий шаг прост — разделите ширину «А» пополам и проведите главную ось симметрии цилиндра посередине.
- Если мы увидим цилиндр сверху, его верхняя круговая плоскость будет выглядеть как эллипс. Измерьте его высоту как относительную пропорцию к ширине или высоте цилиндра. Отметьте на чертеже высоту этой верхней плоскости «С».
- Нарисуйте главную ось овала. Он идет по горизонтали немного не по центру, поэтому размер «E» немного больше, чем «D».
 Это происходит потому, что все объекты, находящиеся ближе к зрителю, в перспективе кажутся больше, чем объекты, расположенные дальше. Одна часть овала ближе к нам, чем другая, поэтому E > D.
Это происходит потому, что все объекты, находящиеся ближе к зрителю, в перспективе кажутся больше, чем объекты, расположенные дальше. Одна часть овала ближе к нам, чем другая, поэтому E > D.
5. Нарисуйте верхнюю плоскость. Это будет эллипс, когда мы увидим перед собой цилиндр. Это может быть овал, если учесть другие искажения перспективы. Использование терминов «эллипс» и «овал» — тема для отдельного разговора. Термин «овал» включает в себя определение «эллипс» и не требует каких-либо оговорок об искажении, поэтому я буду использовать это слово в целях данного объяснения.
6. Следующий шаг – сравнить в жизни, насколько верхний овал больше нижнего. Если объект не сделан из стекла и не прозрачен, вы не увидите всю высоту нижнего овала и должны будете угадать.
7. Отметьте эту высоту на чертеже и разделите ее на две части, следя за тем, чтобы часть «Н», которая ближе к нам, была немного больше, чем «I».
8. Нарисуйте еще один овал, изображающий нижнюю плоскость цилиндра. Делайте это так, как будто вы можете видеть сквозь объект, а также изображать невидимую часть овала.
Делайте это так, как будто вы можете видеть сквозь объект, а также изображать невидимую часть овала.
Рисование всех объектов прозрачными помогает избежать младших ошибок при построении.
Говоря об ошибках, вот четыре типичных ошибки начинающих художников:
1. Не сглаживайте нижний овал. В нашем примере он самый полный.
2. Не рисуйте острые углы овала. Овалы — это круги в ракурсе. Круги не имеют острых краев, как и овалы.
3. Не рисуйте квадратные или слишком заостренные овалы. Их кривизна должна быть плавной во всех местах.
4. Убедитесь, что овал полностью симметричен относительно своей вторичной (более короткой) оси.
Не забудьте применить правила воздушной перспективы. Те объекты, которые находятся ближе к зрителю, будут казаться более четкими и четкими, чем те, которые находятся дальше и должны быть изображены с меньшим нажимом карандаша и контрастом. В таком неглубоком предмете, как цилиндр, в жизни не увидишь воздушной перспективы.
 Это концы большой и малой осей эллипса
Это концы большой и малой осей эллипса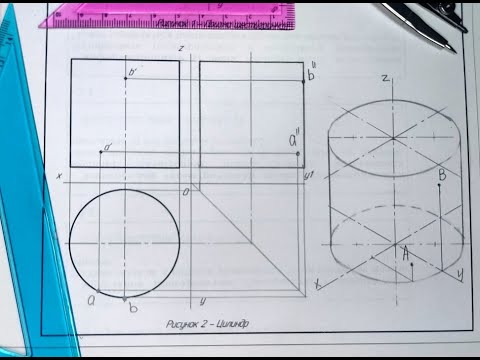 22)
22) Под фигурой понимают любую совокупность (множество) точек. Всякую сложную фигуру можно разделить на более простые.
Под фигурой понимают любую совокупность (множество) точек. Всякую сложную фигуру можно разделить на более простые. Плоскость является частным случаем поверхности.
Плоскость является частным случаем поверхности.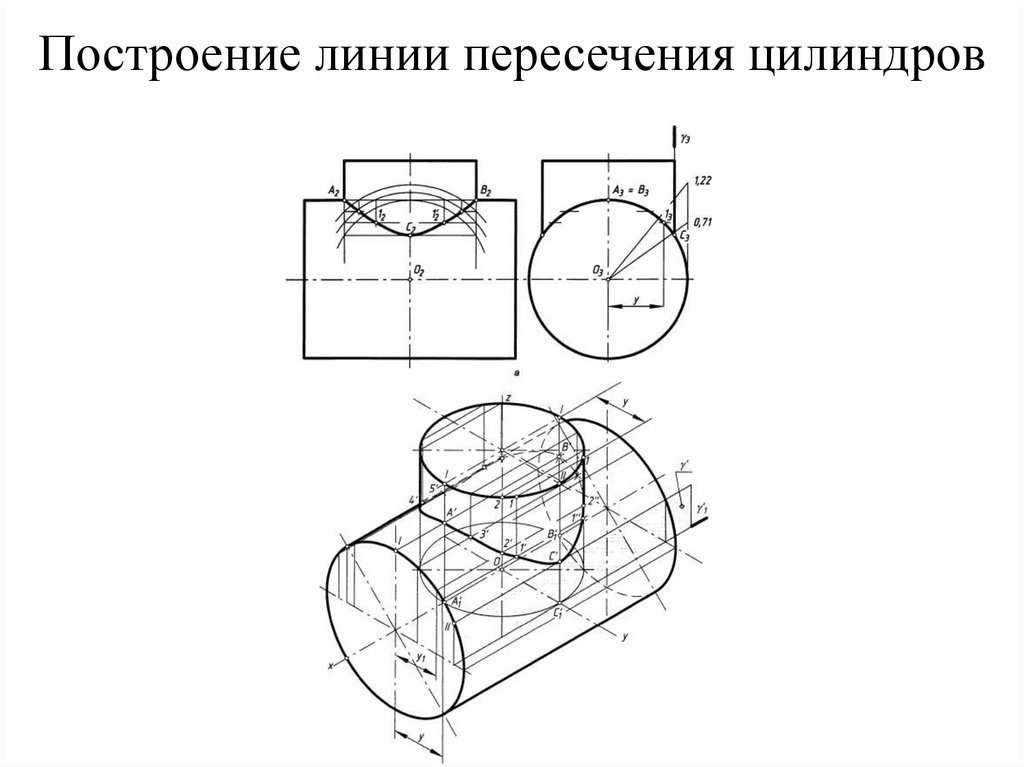 Поэтому рассмотрим сначала построение чертежей и аксонометрических проекций простых тел. Это тем более необходимо, так как в сложной форме любого предмета всегда можно выделить простые геометрические тела, которые помогают представить форму предмета по его чертежу.
Поэтому рассмотрим сначала построение чертежей и аксонометрических проекций простых тел. Это тем более необходимо, так как в сложной форме любого предмета всегда можно выделить простые геометрические тела, которые помогают представить форму предмета по его чертежу. 3. Шестиугольная призма.
3. Шестиугольная призма. 5. Цилиндр
5. Цилиндр
 К геометрическим свойствам предметов относятся: размеры, пропорции, взаимное расположение составляющих элементов формы.
К геометрическим свойствам предметов относятся: размеры, пропорции, взаимное расположение составляющих элементов формы. Для этой цели сложную по форме деталь мысленно разделяют на отдельные конструктивные части, имеющие форму различных геометрических тел. Мысленное разделение предмета на основные геометрические тела называют анализом геометрической формы предмета. Используя изображение детали, размерные числа, условные знаки и надписи, можно воссоздать образ детали, т. е. представить по чертежу ее пространственную форму.
Для этой цели сложную по форме деталь мысленно разделяют на отдельные конструктивные части, имеющие форму различных геометрических тел. Мысленное разделение предмета на основные геометрические тела называют анализом геометрической формы предмета. Используя изображение детали, размерные числа, условные знаки и надписи, можно воссоздать образ детали, т. е. представить по чертежу ее пространственную форму.
 Немного нервное биение по моему нынешнему стулу, чтобы сместить старый, и мне пришлось искать сторонние инструкции по этому процессу, но в целом довольно просто. Абсолютно твердый.
Немного нервное биение по моему нынешнему стулу, чтобы сместить старый, и мне пришлось искать сторонние инструкции по этому процессу, но в целом довольно просто. Абсолютно твердый.

 Это происходит потому, что все объекты, находящиеся ближе к зрителю, в перспективе кажутся больше, чем объекты, расположенные дальше. Одна часть овала ближе к нам, чем другая, поэтому E > D.
Это происходит потому, что все объекты, находящиеся ближе к зрителю, в перспективе кажутся больше, чем объекты, расположенные дальше. Одна часть овала ближе к нам, чем другая, поэтому E > D.