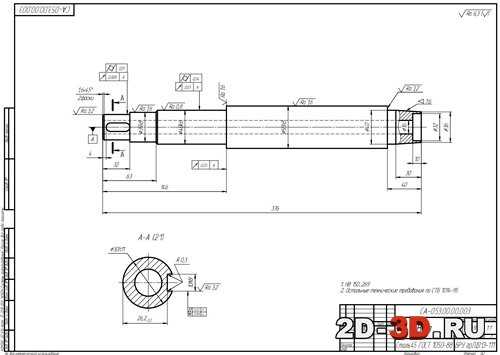
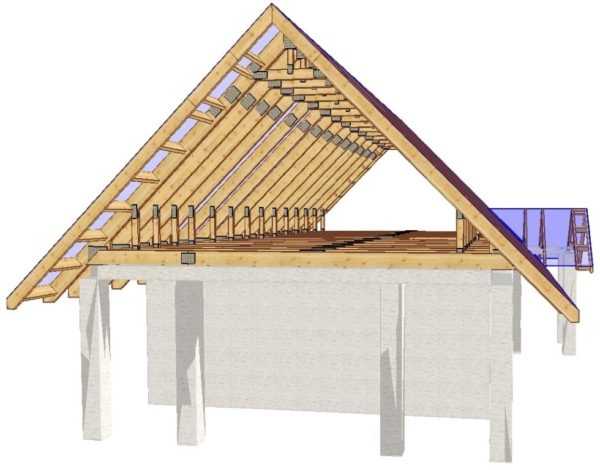
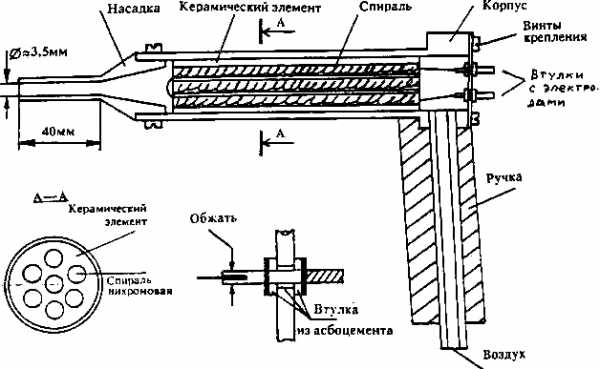
Опорный конспект по геометрии на тему "Цилиндр". Цилиндр в разрезе

Цилиндр как геометрическая фигура

Цилиндр (круговой цилиндр) – тело, которое состоит из двух кругов, совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов. Круги называются основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей кругов, – образующими цилиндра.

Основания цилиндра равны и лежат в параллельных плоскостях, а образующие цилиндра параллельны и равны. Поверхность цилиндра состоит из оснований и боковой поверхности. Боковую поверхность составляют образующие.

Цилиндр называется прямым, если его образующие перпендикулярны плоскостям основания. Цилиндр можно рассматривать как тело, полученное при вращении прямоугольника вокруг одной из сторон как оси. Существуют и другие виды цилиндра – эллиптический, гиперболический, параболический. Призму так же рассматривают, как разновидность цилиндра.

На рисунке 2 изображён наклонный цилиндр. Круги с центрами О и О1 являются его основаниями.

Радиус цилиндра – радиус его основания. Высота цилиндра – расстояние между плоскостями оснований. Осью цилиндра называется прямая, проходящая через центры оснований. Она параллельна образующим. Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением. Плоскость, проходящая через образующую прямого цилиндра и перпендикулярная осевому сечению, проведённому через эту образующую, называется касательной плоскостью цилиндра.

Плоскость, перпендикулярная оси цилиндра, пересекает его боковую поверхность по окружности, равной окружности основания.

Призмой, вписанной в цилиндр, называется такая призма, основания которой – равные многоугольники, вписанные в основания цилиндра. Её боковые рёбра являются образующими цилиндра. Призма называется описанной около цилиндра, если её основания — равные многоугольники, описанные около оснований цилиндра. Плоскости её граней касаются боковой поверхности цилиндра.

Площадь боковой поверхности цилиндра можно вычислить, умножив длину образующей на периметр сечения цилиндра плоскостью, перпендикулярной образующей.

Площадь боковой поверхности прямого цилиндра можно найти по его развёртке. Развёртка цилиндра представляет собой прямоугольник с высотой h и длиной P, которая равна периметру основания. Следовательно, площадь боковой поверхности цилиндра равна площади его развёртки и вычисляется по формуле:

Sb = Ph.

В частности, для прямого кругового цилиндра:

P = 2πR, и Sb = 2πRh.

Площадь полной поверхности цилиндра равна сумме площадей его боковой поверхности и его оснований.

Для прямого кругового цилиндра:

Sp = 2πRh + 2πR2 = 2πR(h + R)

Для нахождения объёма наклонного цилиндра существуют две формулы.

Можно найти объём, умножив длину образующей на площадь сечения цилиндра плоскостью, перпендикулярной образующей.

Объём наклонного цилиндра равен произведению площади основания на высоту (расстояние между плоскостями, в которых лежат основания):

V = Sh = S l sin α,

где l – длина образующей, а α – угол между образующей и плоскостью основания. Для прямого цилиндра h = l.

Формула для нахождения объёма кругового цилиндра выглядит следующим образом:

V = π R2 h = π (d2 / 4)h,

где d – диаметр основания.

blog.tutoronline.ru

Цилиндр. Виды, объём цилиндра, площадь поверхности :: SYL.ru

Название науки «геометрия» переводится как "измерение земли". Зародилась стараниями самых первых древних землеустроителей. А было так: во время разливов священного Нила потоки воды иногда смывали границы участков земледельцев, а новые границы могли не совпасть со старыми. Налоги же крестьянами уплачивались в казну фараона пропорционально величине земельного надела. Измерением площадей пашни в новых границах после разлива занимались специальные люди. Именно в результате их деятельности и возникла новая наука, получившая развитие в Древней Греции. Там она и название получила, и приобрела практически современный вид. В дальнейшем термин стал интернациональным названием науки о плоских и объёмных фигурах.

Планиметрия – раздел геометрии, занимающийся изучением плоских фигур. Другим разделом науки является стереометрия, которая рассматривает свойства пространственных (объёмных) фигур. К таким фигурам относится и описываемая в этой статье – цилиндр.

Примеров присутствия предметов цилиндрической формы в повседневной жизни предостаточно. Цилиндрическую (гораздо реже – коническую) форму имеют почти все детали вращения - валы, втулки, шейки, оси и т.д. Цилиндр широко используется и в строительстве: башни, опорные, декоративные колонны. А кроме того посуда, некоторые виды упаковки, трубы всевозможных диаметров. И наконец – знаменитые шляпы, ставшие надолго символом мужской элегантности. Список можно продолжать бесконечно.

Определение цилиндра как геометрической фигуры

Цилиндром (круговым цилиндром) принято называть фигуру, состоящую из двух кругов, которые при желании совмещаются с помощью параллельного переноса. Именно эти круги и являются основаниями цилиндра. А вот линии (прямые отрезки), связывающие соответствующие точки, получили название «образующие».

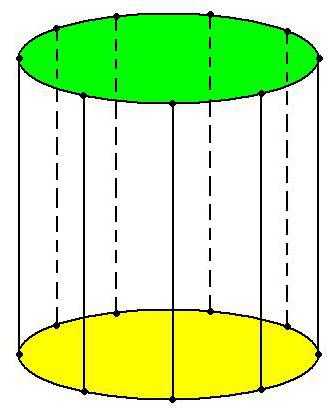
Важно, что основания цилиндра всегда равны (если это условие не выполняется, то перед нами – усечённый конус, что-либо другое, но только не цилиндр) и находятся в параллельных плоскостях. Отрезки же, соединяющие соответствующие точки на кругах, параллельны и равны.

Совокупность бесконечного множества образующих - не что иное, как боковая поверхность цилиндра – один из элементов данной геометрической фигуры. Другая её важная составляющая – рассмотренные выше круги. Называются они основаниями.

Виды цилиндров

Самый простой и распространённый вид цилиндра – круговой. Его образуют два правильных круга, выступающих в роли оснований. Но вместо них могут быть и другие фигуры.

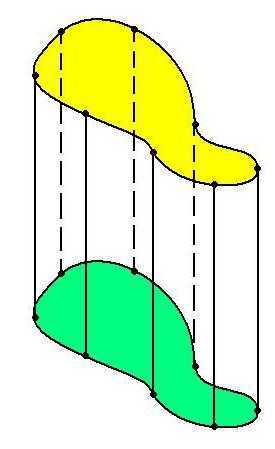
Основания цилиндров могут образовывать (кроме кругов) эллипсы, другие замкнутые фигуры. Но цилиндр может иметь не обязательно замкнутую форму. Например основанием цилиндра может служить парабола, гипербола, другая открытая функция. Такой цилиндр будет открытым или развернутым.

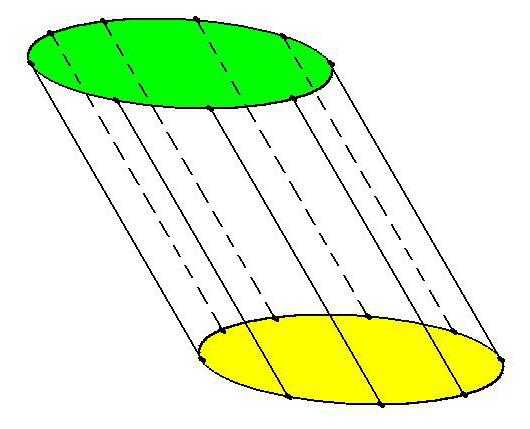
По углу наклона образующих к основаниям цилиндры могут быть прямыми или наклонными. У прямого цилиндра образующие строго перпендикулярны плоскости основания. Если данный угол отличается от 90°, цилиндр – наклонный.

Что такое поверхность вращения

Прямой круговой цилиндр, без сомнения – самая распространённая поверхность вращения, используемая в технике. Иногда по техническим показаниям применяется коническая, шарообразная, некоторые другие типы поверхностей, но 99% всех вращающихся валов, осей и т.д. выполнены именно в форме цилиндров. Для того чтобы лучше уяснить, что такое поверхность вращения, можно рассмотреть, как же образован сам цилиндр.

Допустим, имеется некая прямая a, расположенная вертикально. ABCD – прямоугольник, одна из сторон которого (отрезок АВ) лежит на прямой a. Если вращать прямоугольник вокруг прямой, как это показано на рисунке, объём, который он займёт, вращаясь, и будет нашим телом вращения – прямым круговым цилиндром с высотой H = AB = DC и радиусом R = AD = BC.

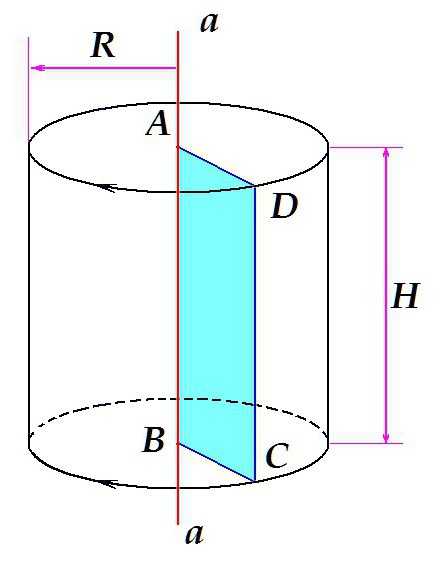
В данном случае, в результате вращения фигуры - прямоугольника - получается цилиндр. Вращая треугольник, можно получить конус, вращая полукруг – шар и т.д.

Площадь поверхности цилиндра

Для того чтобы вычислить площадь поверхности обычного прямого кругового цилиндра, необходимо подсчитать площади оснований и боковой поверхности.

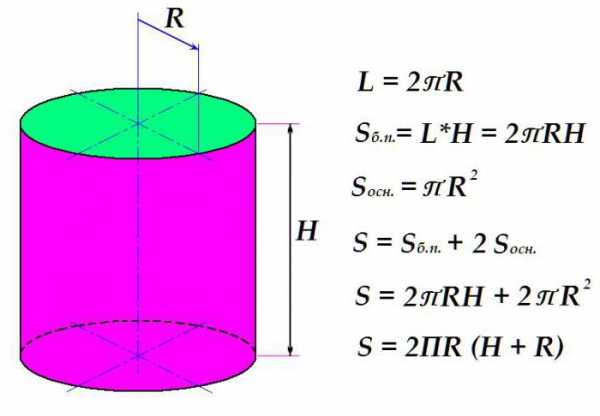
Вначале рассмотрим, как вычисляют площадь боковой поверхности. Это произведение длины окружности на высоту цилиндра. Длина окружности, в свою очередь, равняется удвоенному произведению универсального числа П на радиус окружности.

Площадь круга, как известно, равняется произведению П на квадрат радиуса. Итак, сложив формулы для площади определения боковой поверхности с удвоенным выражением площади основания (их ведь два) и произведя нехитрые алгебраические преобразования, получаем окончательное выражение для определения площади поверхности цилиндра.

Определение объёма фигуры

Объем цилиндра определяется по стандартной схеме: площадь поверхности основания умножается на высоту.

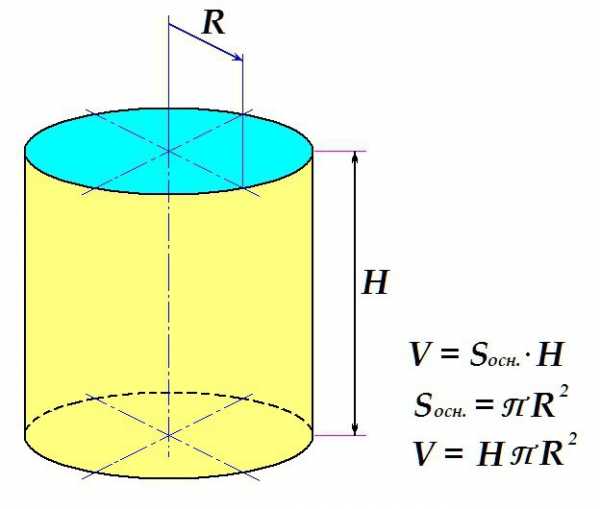
Таким образом, конечная формула выглядит следующим образом: искомое определяется как произведение высоты тела на универсальное число П и на квадрат радиуса основания.

Полученная формула, надо сказать, применима для решения самых неожиданных задач. Точно так же, как объем цилиндра, определяется, например, объём электропроводки. Это бывает необходимо для вычисления массы проводов.

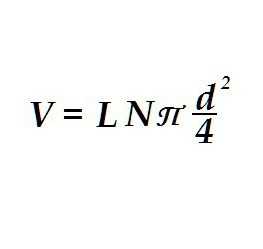
Отличия в формуле только в том, что вместо радиуса одного цилиндра стоит делённый надвое диаметр жилы проводки и в выражении появляется число жил в проводе N. Также вместо высоты используется длина провода. Таким образом рассчитывается объем «цилиндра» не одного, а по числу проводков в оплётке.

Такие расчёты часто требуются на практике. Ведь значительная часть ёмкостей для воды изготовлена в форме трубы. И вычислить объем цилиндра часто бывает нужно даже в домашнем хозяйстве.

Однако, как уже говорилось, форма цилиндра может быть разной. И в некоторых случаях требуется рассчитать, чему равен объем цилиндра наклонного.

Отличие в том, что площадь поверхности основания умножают не на длину образующей, как в случае с прямым цилиндром, а на расстояние между плоскостями – перпендикулярный отрезок, построенный между ними.

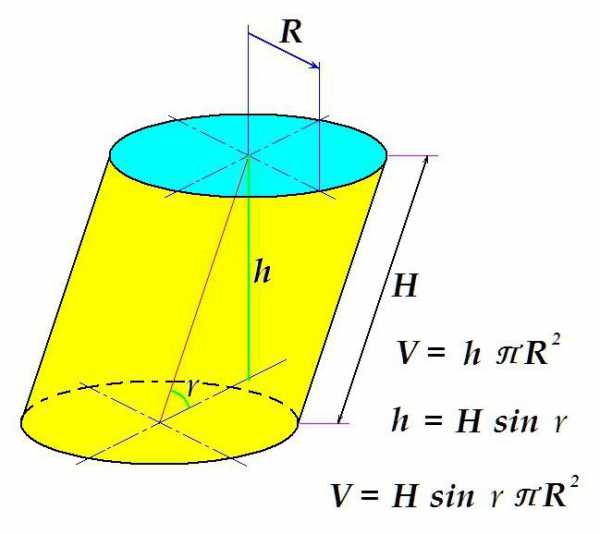
Как видно из рисунка, такой отрезок равен произведению длины образующей на синус угла наклона образующей к плоскости.

Как построить развёртку цилиндра

В некоторых случаях требуется выкроить развёртку цилиндра. На приведённом рисунке показаны правила, по которым строится заготовка для изготовления цилиндра с заданными высотой и диаметром.

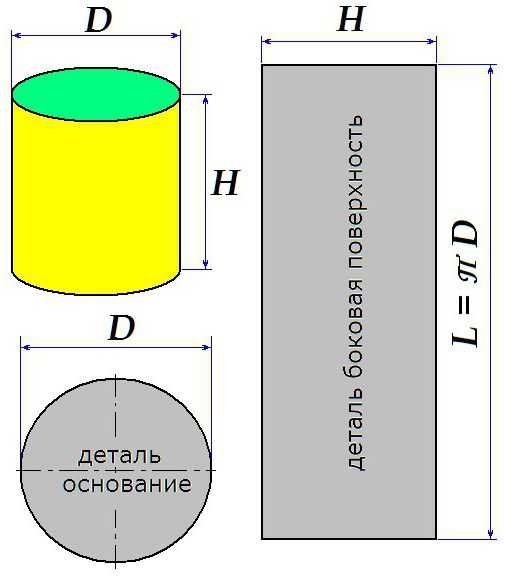
Следует учитывать, что рисунок приведен без учёта швов.

Отличия скошенного цилиндра

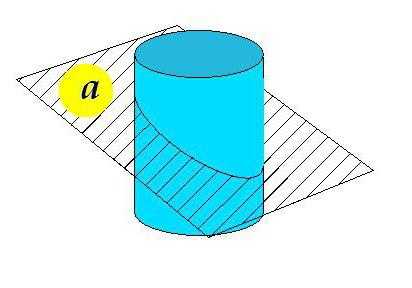
Представим себе некий прямой цилиндр, ограниченный с одной стороны плоскостью, перпендикулярной образующим. А вот плоскость, ограничивающая цилиндр с другой стороны, не перпендикулярна образующим и не параллельна первой плоскости.

На рисунке представлен скошенный цилиндр. Плоскость а под неким углом, отличным от 90° к образующим, пересекает фигуру.

Такая геометрическая форма чаще встречается на практике в виде соединений трубопроводов (колена). Но бывают даже здания, построенные в виде скошенного цилиндра.

Геометрические характеристики скошенного цилиндра

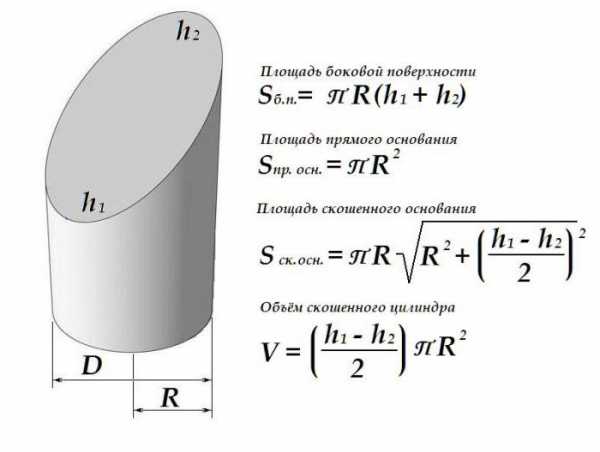
Наклон одной из плоскостей скошенного цилиндра слегка изменяет порядок расчёта как площади поверхности такой фигуры, так и ее объёма.

www.syl.ru

Опорный конспект по геометрии на тему "Цилиндр"

Цилиндр

Опр. Цилиндром называется тело, которое состоит из двух кругов, совмещаемых

параллельным переносом и всех отрезков, соединяющих соответствующие точки

этих кругов.

Круги называют основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей этих кругов – образующими цилиндра (рис. 1)

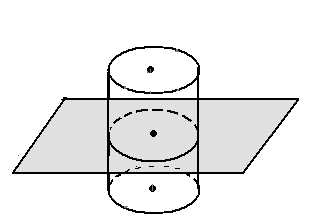
рис. 1 рис. 2 рис. 3 рис. 4

Свойства цилиндра:

1) Основания цилиндра равны и лежат в параллельных плоскостях.

2) Образующие цилиндра равны и параллельны.

Опр. Радиусом цилиндра называется радиус его основания.

Опр. Высотой цилиндра называется расстояние между плоскостями его оснований.

Опр. Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением.

Осевое сечение цилиндра – прямоугольник со сторонами 2R и l (в прямом цилиндре l = Н) рис. 2

Сечение цилиндра, параллельные его оси, являются прямоугольниками (рис. 3).

Сечение цилиндра плоскостью, параллельной основаниям – круг, равный основаниям (рис. 4)

Площадь поверхности цилиндра.

Боковая поверхность цилиндра составлена из образующих.

Полная поверхность цилиндра состоит из оснований и боковой поверхности.

Sполн = 2Sосн + Sбок; Sосн = П∙R2; Sбок = 2П∙R∙Н Sполн = 2ПR∙(R + Н)

Практическая часть:

№1. Радиус цилиндра равен 3см, а его высота- 5см. Найдите площадь осевого сечения и площадь пол-

ной поверхности цилиндра.

№2. Диагональ осевого сечения цилиндра наклонена к плоскости основания под углом 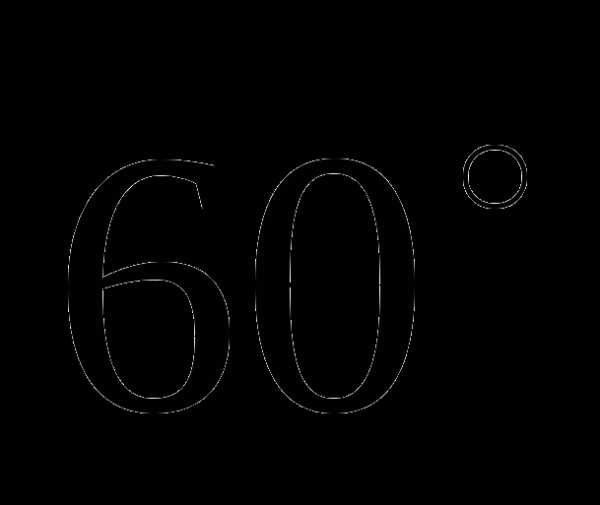и равна 20 см. Найдите площадь боковой поверхности цилиндра.

№3. Радиус цилиндра равен 2см, а его высота- 3см. Найдите диагональ осевого сечения цилиндра.

№4. Диагональ осевого сечения цилиндра, равная 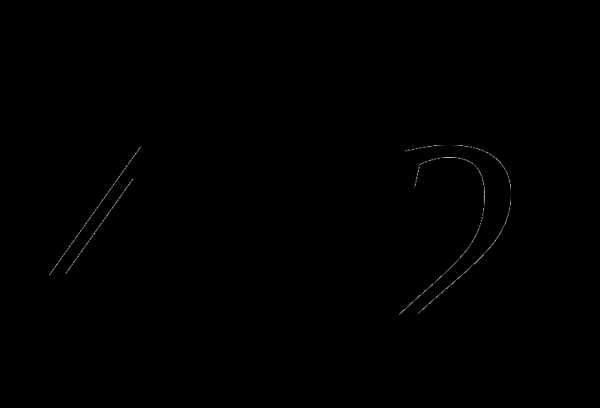, образует с плоскостью основания угол 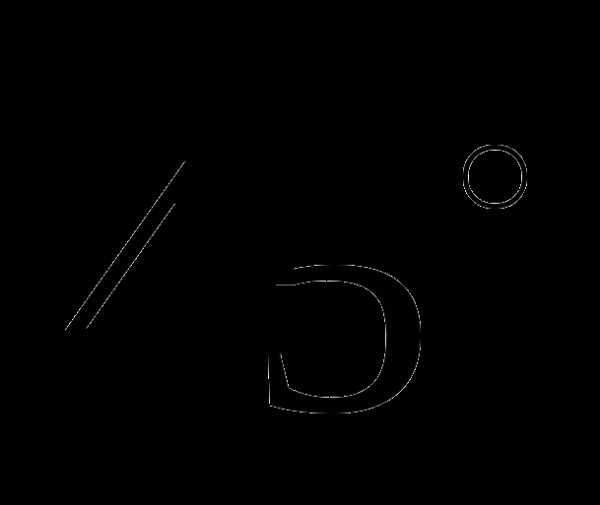. Найдите площадь боковой поверхности цилиндра.

№5. Площадь боковой поверхности цилиндра равна 15. Найдите площадь осевого сечения.

№6. Найдите высоту цилиндра, если площадь его основания равна 1, а S бок = .

№7. Диагональ осевого сечения цилиндра имеет длину 8см и наклонена к плоскости основания под углом 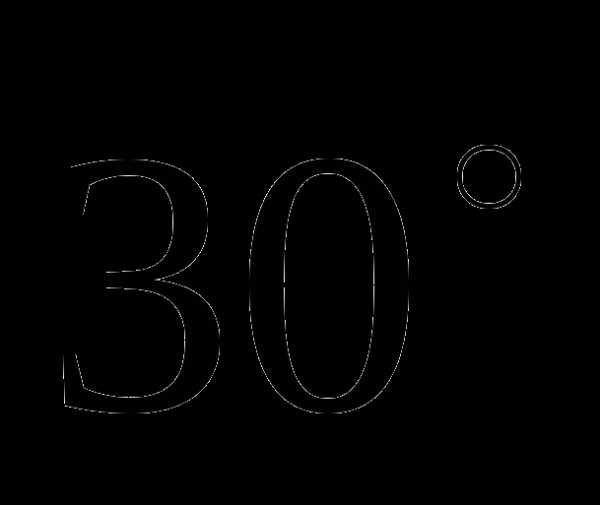. Найдите полную поверхность цилиндра.

№8.

Цилиндрическая дымовая труба с диаметром 65см имеет высоту 18м. Сколько жести нужно для её изготовления, если на заклепку уходит 10% материала?

infourok.ru

Понятие цилиндра

На этом уроке мы вспомним понятие цилиндра. Дадим его определение. Рассмотрим, какими элементами обладает цилиндр.

Вокруг нас существует множество объектов, которые являются физическими моделями цилиндра, или проще говоря, имеют форму цилиндра.

Например, кружки и стаканы имеют форму цилиндра. Карандаши, шляпы, пуфики, барабан также имеют форму цилиндра.

Некоторые архитектурные сооружения.

Колонны храмов и соборов, выполненные в форме цилиндра, подчеркивают их гармонию и красоту.

Итак, перейдём к самому цилиндру. Рассмотрим произвольную плоскость и окружность с центром О радиуса , лежащую в этой плоскости. Через каждую точку окружности проведем прямую, перпендикулярную к плоскости .

Определение:

Поверхность, образованная этими прямыми, называется цилиндрической поверхностью, а сами прямые – образующими цилиндрической поверхности.

Прямая, проходящая через точку О перпендикулярно к плоскости , называется осью цилиндрической поверхности. Поскольку все образующие и ось перпендикулярны к плоскости , то они параллельны друг другу.

Рассмотрим теперь плоскость , параллельную плоскости . Отрезки образующих, заключённые между плоскостями и , параллельны и равны друг другу. По построению концы этих отрезков, расположенные в плоскости , заполняют окружность . Концы же, расположенные в плоскости , заполняют окружность с центром радиуса , где – точка пересечения плоскости с осью цилиндрической поверхности. Справедливость этого утверждения следует из того, что множество концов образующих, лежащих в плоскости , получается из окружности параллельным переносом на вектор . Параллельный перенос является движением и, значит, наложением, а при наложении любая фигура переходит в равную ей фигуру. Следовательно, при параллельном переносе на вектор . окружность перейдёт в равную ей окружность радиуса с центром в точке .

Определение:

Тело, ограниченное цилиндрической поверхностью и двумя равными кругами с границами и , называется цилиндром.

Можно ещё услышать и такое определение: прямым круговым цилиндром или просто цилиндром называется геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями и , которые перпендикулярны образующим цилиндрической поверхности.

Назовём элементы цилиндра.

Круги называются основаниями цилиндра.

Отрезки образующих, заключенные между основаниями, - образующими цилиндра.

А образованная ими часть цилиндрической поверхности это есть боковая поверхность цилиндра.

Ось цилиндрической поверхности называется осью цилиндра.

Как уже отмечалось ранее, все образующие цилиндра параллельны и равны друг другу. Длина образующей называется высотой цилиндра, а радиус основания – радиусом цилиндра.

Цилиндр называется равносторонним, если его высота равна диаметру основания.

Боковой поверхностью цилиндра называется часть цилиндрической поверхности, расположенная между основаниями цилиндра.

Цилиндр можно получить вращением прямоугольника вокруг одной из его сторон на . Итак, если взять некоторый прямоугольник и вращать его вокруг одной из сторон, например, вокруг стороны , то в результате получим тело, которое и называется цилиндром.

В этом случае основания цилиндра образуются вращением сторон и , а боковая поверхность цилиндра образуется вращении стороны .

Теперь рассмотрим сечения цилиндра различными плоскостями.

Если секущая плоскость проходит через ось цилиндра, то сечение представляет собой прямоугольник, две стороны которого – образующие, а две другие – диаметры оснований цилиндра. Такое сечение называется осевым.

Определение:

Осевым сечением цилиндра называется сечение цилиндра плоскостью, проходящей через его ось.

Если секущая плоскость параллельна оси цилиндра, то сечением цилиндра служит прямоугольник, две стороны которого – образующие цилиндра, а две другие – хорды оснований цилиндра.

Если секущая плоскость перпендикулярна к оси цилиндра, то сечение является кругом.

В самом деле, такая секущая плоскость отсекает от данного цилиндра тело, которое также является цилиндром. Его основаниями служат два круга, один из которых и есть рассматриваемое сечение.

Замечание. На практике очень часто встречаются предметы, которые имеют форму сложных цилиндров.

На экране, на первом рисунке вы видите цилиндр, каждое основание которого представляет собой фигуру, ограниченную частью параболы и отрезком. На втором рисунке изображен цилиндр, основаниями которого являются круги, но образующие цилиндра не перпендикулярны к плоскостям оснований, такой цилиндр называют еще наклонным цилиндром. Однако в дальнейшем мы будем рассматривать только прямые круговые цилиндры.

Задача: точка – середина образующей цилиндра, центрами оснований которого являются точки и . Верно ли, что ?

Решение: рассмотрим и .

Образующая перпендикулярна плоскостям, в которых лежат основания цилиндра. Следовательно, она перпендикулярна любой прямой лежащей в этих плоскостях. Прямые и являются радиусами цилиндра и лежат в плоскостях оснований. Значит, прямая и . Отсюда получаем, что и – прямоугольные.

Так как основаниями цилиндра являются равные круги, то , как радиусы.

Так как по условию задачи точка – середина образующей цилиндра, то отрезки . Значит, равны по двум катетам. Отсюда вытекает, что .

Ответ: .

Задача: точка – центр основания цилиндра. Отрезок – диаметр другого его основания. Вычислите площадь , если радиус цилиндра равен см, а его высота – см.

Решение: напомним, что площадь треугольника находится по формуле . Заметим, что высота цилиндра является и высотой нашего и равна . А основание треугольника есть диаметр цилиндра и равно оно двум радиусам, т.е. (см).

Подставим в формулу площади треугольника высоту и длину основания треугольника. Посчитаем. Получим, что площадь треугольника равна . Не забудем записать ответ.

Задача: радиус цилиндра см, а его высота – см. Вычислите площадь осевого сечения.

Решение: напомним, что осевым сечением цилиндра называется сечение цилиндра плоскостью, проходящей через его ось. Осевое сечение цилиндра представляет собой прямоугольник, две стороны которого – образующие, а две другие – диаметры оснований цилиндра.

Высота цилиндра – это есть длина образующей . Следовательно, ширина осевого сечения равна . Длина сечения равна диаметру основания цилиндра. И значит, равна (см).

Теперь вычислим площадь осевого сечения. Она равна ().

Запишем ответ.

Итоги:

На этом уроке мы вспомнили понятие цилиндра. Узнали, что тело, ограниченное цилиндрической поверхностью и двумя кругами с границами и , называется цилиндром. Или прямым круговым цилиндром или просто цилиндром называется геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями и , которые перпендикулярны образующим цилиндрической поверхности. Назвали элементы цилиндра. А также рассмотрели сечения цилиндра различными плоскостями.

videouroki.net

Цилиндр [wiki.eduVdom.com]

Цилиндром (прямым круговым цилиндром) называется тело, состоящее из двух кругов (оснований цилиндра), совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие при параллельном переносе точки этих кругов. Отрезки, соединяющие соответствующие точки окружностей оснований, называются образующими цилиндра.

Цилиндр является телом вращения.

Цилиндр

Рис.1

Вот другое определение:

Цилиндр — тело, которое ограничено цилиндрической поверхностью с замкнутой направляющей и двумя параллельными плоскостями, пересекающими образующие данной поверхности.

Цилиндрическая поверхность — поверхность, которая образуется движением прямой линии вдоль некоторой кривой. Прямую называют образующей цилиндрической поверхности, а кривую линию — направляющей цилиндрической поверхности.

Боковая поверхность цилиндра — часть цилиндрической поверхности, которая ограничена параллельными плоскостями.

Основания цилиндра — части параллельных плоскостей, отсекаемые боковой поверхностью цилиндра.

Рис.1 мини

Цилиндр называется прямым (См.Рис.1), если его образующие перпендикулярны плоскостям оснований. В противном случае цилиндр называется наклонным.

Круговой цилиндр — цилиндр, основания которого являются кругами.

Прямой круговой цилиндр (просто цилиндр) – это тело, полученное при вращении прямоугольника вокруг одной из его сторон. См.Рис.1.

Радиус цилиндра – радиус его основания.

Образующая цилиндра — образующая цилиндрической поверхности.

Высотой цилиндра называется расстояние между плоскостями оснований. Осью цилиндра называется прямая, проходящая через центры оснований. Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением.

Ось цилиндра параллельна его образующей и является осью симметрии цилиндра.

Плоскость, проходящая через образующую прямого цилиндра и перпендикулярная осевому сечению, проведенному через эту образующую, называется касательной плоскостью цилиндра. См.Рис.2.

Рис.2

Развёртка боковой поверхности цилиндра — прямоугольник со сторонами, равными высоте цилиндра и длине окружности основания.

Площадь боковой поверхности цилиндра — площадь развёртки боковой поверхности. $$S_{бок}=2\pi\cdot rh$$ , где h – высота цилиндра, а r – радиус основания.

Площадь полной поверхности цилиндра — площадь, которая равна сумме площадей двух оснований цилиндра и его боковой поверхности, т.е. выражается формулой: $$S_{полн}=2\pi\cdot r^2 + 2\pi\cdot rh = 2\pi\cdot r(r+h)$$ , где h – высота цилиндра, а r – радиус основания.

Объем всякого цилиндра равен произведению площади основания на высоту: $$V = S\cdot h$$ Объем круглого цилиндра: $$V=\pi r^2 \cdot h$$ , где (r — радиус основания).

Призма есть частный вид цилиндра (образующие параллельны боковым ребрам; направляющая — многоугольник, лежащий в основании). С другой стороны, произвольный цилиндр можно рассматривать как выродившуюся («сглаженную») призму с очень большим числом очень узких граней. Практически цилиндр неотличим от такой призмы. Все свойства призмы сохраняются и в цилиндре.

wiki.eduvdom.com

Сечения цилиндра - Энциклопедия по машиностроению XXL

В предыдущих параграфах были рассмотрены кривые линии, полученные в результате плоских сечений цилиндра и конуса, а также чертежи плоских деталей со сложным криволинейным контуром. Рассмотрим чертежи деталей с криволинейными поверхностями. [c.225]

СЕЧЕНИЕ ЦИЛИНДРА ПЛОСКОСТЬЮ [c.96]

Примером плоского сечения цилиндра может служить часть пылесборника машины для очистки литых деталей (рис. 174, я). Плоская крышка А трубы пылесборника наклонена к оси трубы и ограничена эллипсом. [c.98]

Строим нормальное сечение цилиндра плоскостью Qyi ]л определяем натуральную величину линии сечения. [c.291]

Пример. Построить наклонное сечение цилиндра плоскостью (рис. 121). [c.134]

Заданная секущая плоскость пересекает только цилиндрическую поверхность. Следовательно, в сечении цилиндра получаем плоскую фигуру, ограниченную эллипсом (см. 32). Большая ось эллипса равна отрезку 1-5-, а малая — отрезку 3 7 (диаметру цилиндра). [c.134]

Строим новую проекцию линии сечения цилиндра плоскостью А—А, используя приведенные ранее в п. 6.4 правила. [c.135]

Границами сечения цилиндра плоскостью типа у (рис. 153) параллельной оси вращения являются образующие, проходящие через точки (1-2), (Г-2 ). На фронтальной проекции конкурирующие точки 1 и 2 г не обозначены, чтобы не загромождать изображения. Этот приём используется и в других примерах. [c.151]

Рассмотрим применение способа на примере пересечения прямого кругового конуса с осью вращения 1(12) и эллиптического цилиндра с осью симметрии 4(42) (рис. 189). В сечении цилиндра плоскостью, перпендикулярной оси я(я2), будут эллипсы, а в сечении под углом (р, изображенном как основание цилиндра, будут окружности диаметра (1. Эти окружности называют круговыми сечениями." Не трудно догадаться, что у этого цилиндра есть ещё одно направление, в котором сечения тоже будут круговыми. [c.189]

Поскольку количество точек для построения лекальных кривых определяется количеством частей, на которые делится нормальное сечение цилиндра, оно зависит от необходимой степени точности выполнения развертки. Отметим, не приводя доказательств, что кривые, ограничивающие построенную развертку, являются синусоида ми. [c.119]

Так как деформация при кручении зависит от величины крутящего момента, действующего в данном сечении, необходимо рассмотреть методику определения крутящего момента в любом сечении цилиндра. В месте закрепления цилиндра (рис. 131, б) возникает реактивный крутящий момент Л1р, равный внешнему крутящему моменту М, приложенному к свободному концу цилиндра. Рассечем цилиндр плоскостью / и рассмотрим равновесие его нижней части (рис. 131, в). Для нахождения нижней части в равновесии необходимо, чтобы момент внутренних сил упругости в данном сечении уравновешивал реактивный момент Мр, равный М [c.188]

Таким образом, крутящий момент, действующий в любом сечении цилиндра, являющийся моментом внутренних сил упругости, численно равен моменту внешней пары сил, действующей по любую сторону от сечения. [c.188]

Пс закону Гука напряжение в сечении цилиндра [c.191]

Сумма таких элементарных моментов, взятая, по всей площади поперечного сечения цилиндра, равна крутящему моменту М р, который действует в рассматриваемом сечении цилиндра и в данном конкретном случае равен внешнему моменту М [c.191]

На основании этого цилиндр можно рассматривать как составленный из отдельных колец, нанизанных на ось. Поперечные сечения цилиндра при деформации остаются плоскими, [c.447]

Нормальным сечением цилиндра называется сечение, перпендикулярное к его образующим. У эллиптического цилиндра, как известно ( 30), нормальным сечением является эллипс. Для задания секущей плоскости [c.162]

На чертеже показано построение точек А, В, С, О, Е, Р, О и Н натурального вида сечения. Эти точки построены при помощи их высот и широт. Эллипсы, которые получаются в сечениях цилиндров, построены по их осям, при этом малая ось каждого эллипса равна диаметру соответствующего цилиндра, а большая — отрезку проекции Е 2. заключенному между проекциями очерковых образующих цилиндра. [c.165]

Прямая строфоида — фокаль эллиптических сечений цилиндра, когда ось пучка секущих плоскостей проходит через точку А перпендикулярно к осевому сечению цилиндра АОу. Циссоида — место точек М (рис. 2, д), [c.21]

Заметим, что в силу тонкостенности кольца, представляющего собой сечение цилиндра, по которому действуют напряжения 02, площадь его подсчитана как произведение длины окружности на толщину стенки. [c.262]

Радиальное перемещение произвольно взятой точки обозначим через и. Величина и является функцией текущего радиуса г и не изменяется по длине цилиндра. За положительное направление для г примем направление от оси цилиндра (рис. 309). Что касается перемещений вдоль оси, то будем считать, что они возникают только как следствие общего удлинения или укорочения цилиндра. Если осевые перемещения существуют, то они распределены так, что поперечные сечения цилиндра остаются плоскими. [c.276]

В сечениях цилиндра (как осевых, так и поперечных) возникают изгибающие моменты и нормальные силы. Они определяются через напряжения и о ,, аналогично тому, как это делалось для круглой пластины. [c.317]

Развертка цилиндра вращения. Выбирают горизонтальную прямую линию и на нен спрямляют линию нормального сечения цилиндра вращения — окружность радиусом г. Строят развертку боковой поверхности цилиндра. На развертке помечают прямолинейные образующие, проходящие через характерные точки линии пересечения цилиндра с конусом. Эти точки замечают на соответствующих образующих, Они определяют линию пересечения поверхностей на развертке. Полная развертка цилиндра вращения представляется разверткой его боковой поверхности и основаниями — окружностями радиуса г. [c.20]

Натуральный вид фигуры сечения цилиндра плоскостью Р построен способом перемены плоскостей проекций на плоскости перпендикулярной плоскости V. Большая ось эллипса — отрезок 1,7,Г 7, малая — отрезок 4,10,= 4. [c.112]

Переносное нормальное ускорение wl точки М направлено по радиусу МО, кругового сечения цилиндра, проходящего через точку /И, причем [c.216]

Таким образом, радиус кривизны винтовой линии с постоянным шагом больше, чем радиус / кругового сечения цилиндра. [c.81]

Рассмотрим элемент массы, находящийся между двумя бесконечно близкими поперечными сечениями цилиндра плоскостями, параллельными плоскости хОу (рис. 7,6). Находим [c.61]

В уравнения (h) входят четыре неизвестных хс, q>, R и F Чтобы задача была определенной, необходимо составить еще одно уравнение. В случае качения без скольжения необходимое уравнение можно составить из кинематических соображений. Действительно, в этом случае точка С касания поперечного сечения цилиндра и прямой линии АВ является мгновенным центром скоростей ( 111 т. 1). Поэтому полагаем [c.410]

Здесь с — координаты торцевых сечений цилиндра, нормальных к его образующим. Далее находим [c.489]

Предположим, что боковая поверхность цилиндра свободна от напряжений, а на 5 ) и 5i заданы произвольные силовые воздействия. Из механических соображений ясно, что если характерный размер поперечного сечения цилиндра мал по сравнению с его высотой, то на достаточном удалении от торцов характер распределения внешних воздействий не будет сказываться на напряженно-деформированном состоянии — главную роль будут играть такие интегральные характеристики, как [c.63]

Рассмотрим образование цилиндроида. Возьмем цилиндр (рис. 276), образующими которого являются горизонтальные прямые линии. В данном случае они взяты параллельно и плоскости V. Цилиндр пересечем двумя горизонтально-проецирующими плоскостями Nift м NiH. Эти плоскости между собой пересекаются по вертикальной прямой линии fg, f g. Сечениями цилиндра являются кривые линии аЬ, а Ь и d, d. [c.187]

Все точки производящей перемещаются в плоскостях, перпендикулярных к образующим аксоида-цилиндра. Ходами их точек являются кривые линии, являющиеся эвольвентами линий сечения цилиндра-аксоида этими плоскостями. Проекции таких линий на плоскость Q имеют общую эволюту — направляющунз линию цилиндра-аксоида. [c.364]

Действительно, круговое сечение цилиндра можно принять за параллель некоторой сферы. Например, окружность радиуса ell (рис. 263, 6) может быть параллелью многих сфер, центры которых располагаются на прямой, проведенной через j перпендикулярно к плоскости параллели. Если же мы на этом перпендикуляре возьмем точку в пересечении с осью конуса, то такую точку (с фронт проекцией 0 ) можно принять за центр сферы с радиусом 0 1, пересекающей цилиндр по окруж--НОШХааддаз li э конус вращения — по окружности с диаметром 2 3. Отсюда мы получаем точки, фронт, проекции которых сливаются в одну точку е (одна из этих точек — на обращенной к нам части линии пересечения, другая — на ей симметричной). [c.220]

Сечением цилиндра плоскостью р, образующей острый угол с осью вращения, является эллипс с сопряжёнными диаметрами [АВ] и[СО]. В примере его фронтальная проекция изображается пря.мой [А2В2], горизонтальная проекция - окружностью, а профильная - эллипсом. Плоскость р пересекается с верх-1им основанием цилиндра по прямой 3-3. Толстой линией обведены изображения изделия, полученного из цилиндрической заготовки, срезанной плоскостями. [c.151]

Проведём проецирующую плоскость у(у2) параллельно круговому сечению цилиндра. Она рассечет цилиндр по окружности т(т2), которая изобразится отрезком внутри очерка цилиндра. Из проекции центра ШгПцг окружности [c.189]

Черс прямую т проведена плоскость и>, пересекающая цилиндрическую поверхность по образующим. Для этого, как известно, плоскость должна быть параллельна образующим (или оси) цилиндра. На чертежах она определена прямсж т и прямой а, про ходящей через некоторую точку А прямой т и параллельной оси цилиндра ш т [ а). (Другие плоскости, в частности проецирующие, проходящие через прямую т, дадут в сечении цилиндра более сложные, лекальные кривые линии.) [c.82]

Точка 2 найдена с помЬщъю вспомогательного сечении пршильной плоскостью размер а получен на нормальном сечении цилиндра повернутом во фронтальное п[c.25]

В осевых сечениях цилиндра (плоскость АВСО элемента) по условиям осевой симметрии касательные напряжения отсутствуют и сохраняются только нормальные напряжения а , называемые окружными. В поперечных сечениях цилиндра (поверхность СОЕР элемента) касательные напряжения также предпола1 аются равными нулю. Основанием к этому служит условие независимости перемещений и от координаты г. [c.277]

Так к ж цилир др катится без скольжения, то точка R соприкасания среднего сечення цилиндра с плоскостью является мгновенным центром скоростей среднего сечения. [c.238]

Предположим, что массовые силы отсутствуют и что сечение цилиндра плоскостью Хз = onst— односвязная область в плоскости (xi,. Гг) Для решения задачи применим полуобратный метод, т. е. попытаемся угадать вид некоторых характеристик напряженно-деформировакного состояния, остальные же величины будем искать таким образом, чтобы удовлетворить всем уравнениям теории упругости. [c.64]

Гипотеза (2.116) вытекает из того, что каждое сечение цилиндра плоскостью Хз = onst поворачивается около оси Ох на угол, пропорциональный Хз (а — коэффициент пропорциональности) (2.117) означает, что точки, расположенные на прямой Jt i = onst, 2= onst, смещаются вдоль Oxg на одну и ту же величину. [c.65]

mash-xxl.info

Дайте определение цилиндра как геометрического тела.

Цилиндром называется тело, которое состоит из двух кругов, совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов. Круги называются основаниями цилиндра. а отрезки, соединяющие соответствующие точки окружностей кругов, - образующими цилиндра. Основания цилиндра равны и лежат в параллельных плоскостях. У цилиндра образующие параллельны и равны. Поверхность цилиндра состоит из оснований и боковой поверхности. Боковая поверхность составлена из образующих. Цилиндр называется прямым, если его образующие перпендикулярны плоскостям оснований. Радиусом цилиндра называется радиус его основания. Высотой цилиндра называется расстояние между плоскостями оснований. Осью цилиндра называется прямая, проходящая через центры оснований. Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением. Плоскость, проходящая через образующую прямого цилиндра и перпендикулярная осевому сечению, проведенному через эту образующую, называется касательной плоскостью цилиндра Призмой, вписанной в цилиндр, называется такая призма, основания которой - равные многоугольники, вписанные в основание цилиндра. Ее боковые ребра являются образующими цилиндра. Призма называется описанной около цилиндра. если ее основания - равные многоугольники, описанные около оснований цилиндра. Плоскости ее граней касаются боковой поверхности цилиндра. <img src="//otvet.imgsmail.ru/download/b2cf36e91f7106e56bdf3d081dc1f1f6_i-70.gif" >

Цили́ндр (греч. kýlindros, валик, каток) — геометрическое тело, ограниченное цилиндрической поверхностью (называемой боковой поверхностью цилиндра) и не более чем двумя поверхностями (основаниями цилиндра) ; причём если оснований два, то одно получено из другого параллельным переносом вдоль образующей боковой поверхности цилиндра; и основание пересекает каждую образующую боковой поверхности ровно один раз.

Цилиндр - тело, ограниченное цилиндрической поверхностью с замкнутой направляющей и двумя параллельными плоскостями, являющимися основаниями цилиндра. Цилиндрическая поверхость образуется прямой (образующей) , перемещающейся параллельно заданному направлению вдоль некоторой кривой (направляющей) . Если в основании цилиндра круг, а его образующие перпендикулярны плоскости основания, он называется - круговой прямой цилиндр. Если одно из оснований кругового прямого цилиндра не параллельно второму, он называетяс усечённый круговой цилиндр.

touch.otvet.mail.ru