Содержание
Формулы объема геометрических фигур
Объем геометрической фигуры
— количественная характеристика пространства, занимаемого телом или веществом. Объём тела или вместимость сосуда определяется его формой и линейными размерами.
Навигация по странице:
Формулы объема куба
Формулы объема призмы
Формулы объема параллелепипеда
Формулы объема прямоугольного параллелепипеда
Формулы объема пирамиды
Формулы объема правильного тетраэдра
Формулы объема цилиндра
Формулы объема конуса
Формулы объема шара
Онлайн калькуляторы для вычисления объемов
Объем призмы
Объем призмы равен произведению площади основания призмы, на высоту.
Формула объема призмы:
V = So h
где V — объем призмы,
So — площадь основания призмы,
h — высота призмы.
Онлайн калькулятор для расчета объема призмы
Формулы площади геометрических фигур для определения площади основания призмы
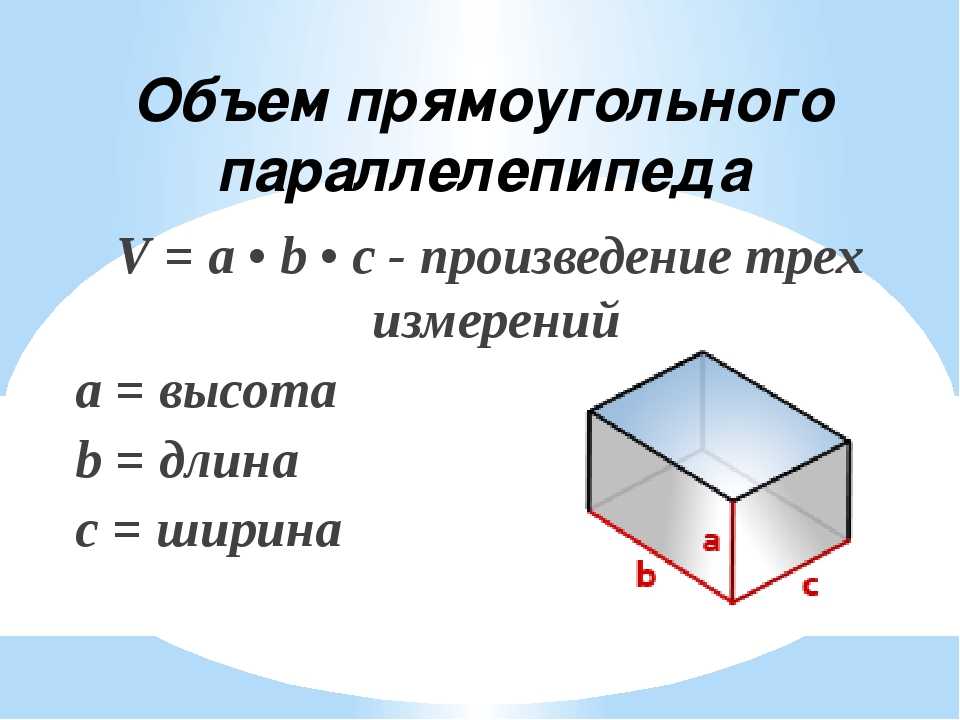
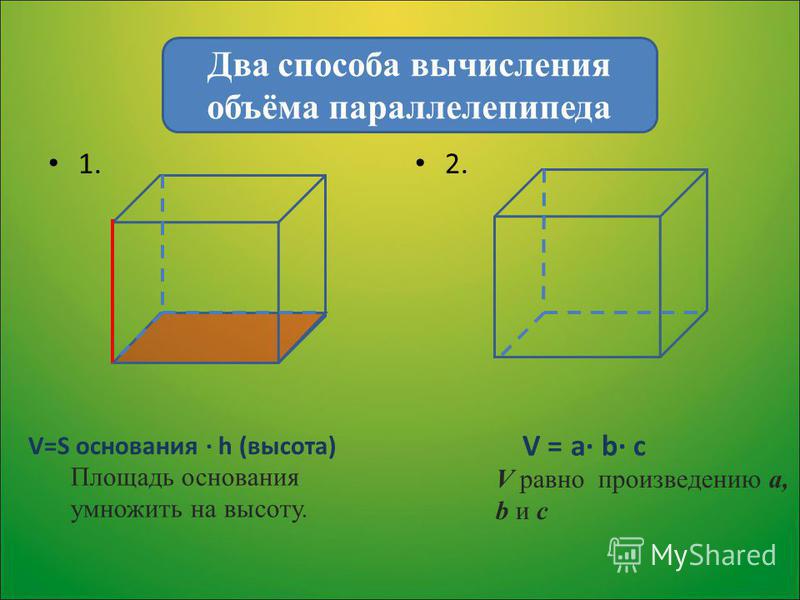
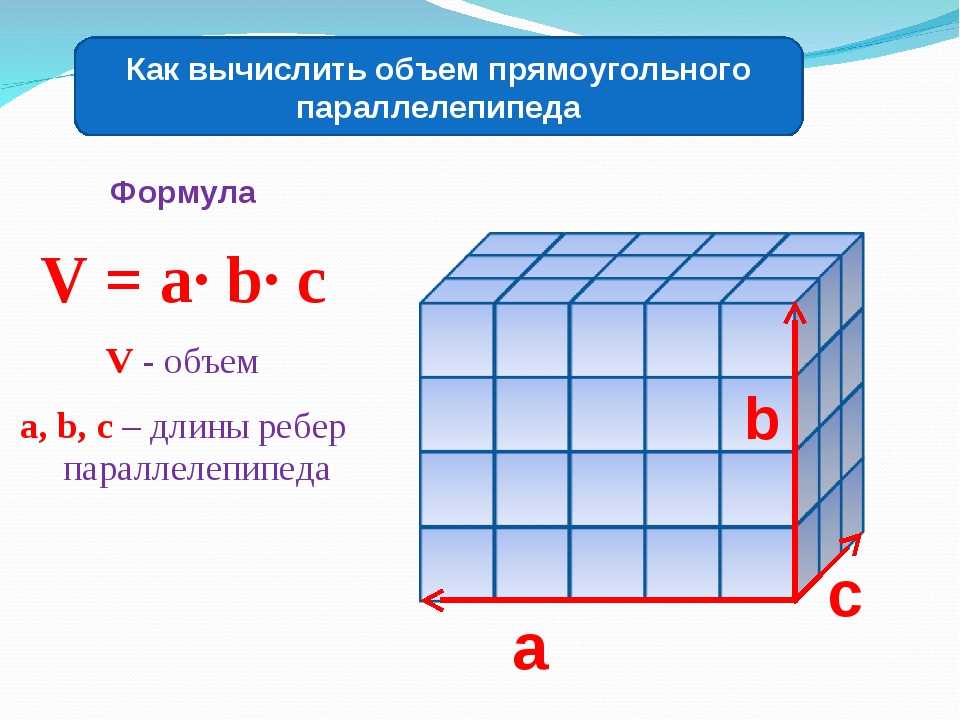
Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
Формула объема прямоугольного параллелепипеда:
V = a · b · h
где V — объем прямоугольного параллелепипеда,
a — длина,
b — ширина,
h — высота.
Смотрите также онлайн калькулятор для расчета объема прямоугольного параллелепипеда
Объем пирамиды
Объем пирамиды равен трети от произведения площади ее основания на высоту.
Формула объема пирамиды:
| V = | 1 | So · h |
| 3 |
где V — объем пирамиды,
So — площадь основания пирамиды,
h — длина высоты пирамиды.
Онлайн калькулятор для расчета объема пирамиды
Формулы площади геометрических фигур для определения площади основания пирамиды
Объем цилиндра
Объем цилиндра равен произведению площади его основания на высоту.
Формулы объема цилиндра:
V = π R2 h
V = So h
где V — объем цилиндра,
So — площадь основания цилиндра,
R — радиус цилиндра,
h — высота цилиндра,
π = 3.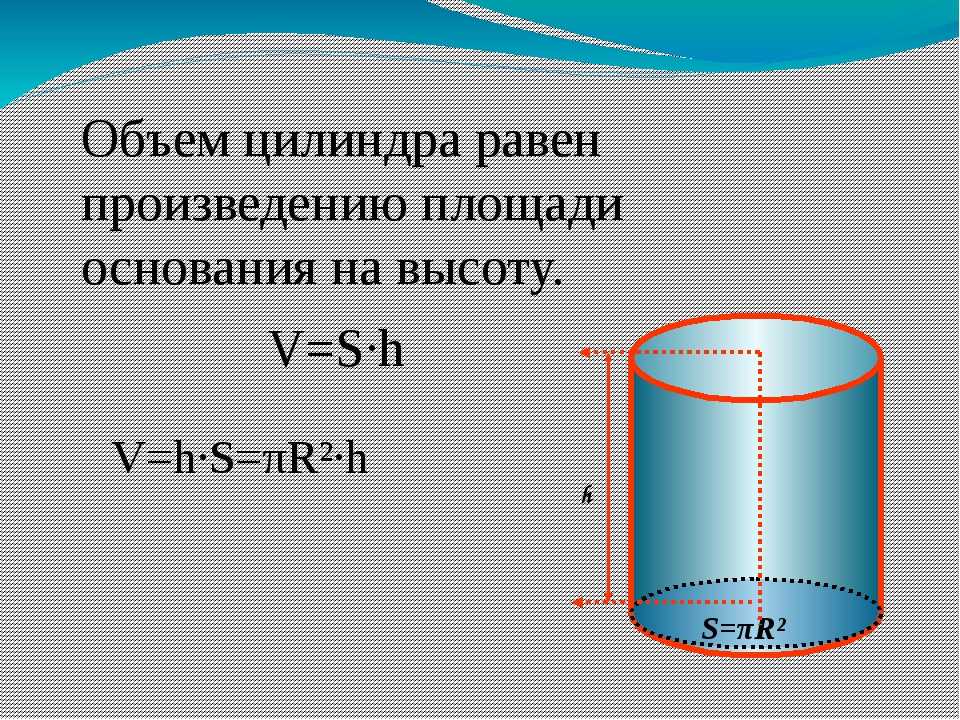 141592.
141592.
Смотрите также онлайн калькулятор для расчета объема цилиндра
Объем конуса
Объем конуса равен трети от произведению площади его основания на высоту.
Формулы объема конуса:
| V = | 1 | π R2 h |
| 3 |
| V = | 1 | So h |
| 3 |
где V — объем конуса,
So — площадь основания конуса,
R — радиус основания конуса,
h — высота конуса,
π = 3.141592.
Смотрите также онлайн калькулятор для расчета объема конуса
Все таблицы и формулы
Все формулы объемов геометрических тел
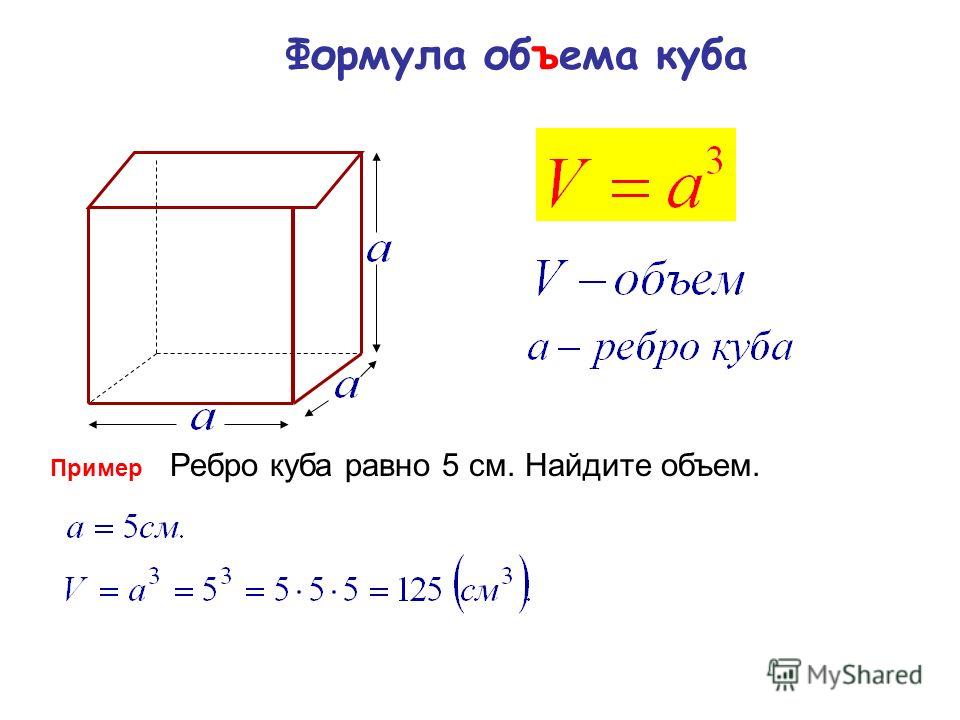
1. Расчет объема куба
a — сторона куба
Формула объема куба, (V):
2.
 Найти по формуле, объем прямоугольного параллелепипеда
Найти по формуле, объем прямоугольного параллелепипеда
a, b, c — стороны параллелепипеда
Еще иногда сторону параллелепипеда, называют ребром.
Формула объема параллелепипеда, (V):
3. Формула для вычисления объема шара, сферы
R — радиус шара
π ≈ 3.14
По формуле, если дан радиус, можно найти объема шара, (V):
4. Как вычислить объем цилиндра ?
h — высота цилиндра
r — радиус основания
π ≈ 3.14
По формуле найти объема цилиндра, есди известны — его радиус основания и высота, (V):
5.
 Как найти объем конуса ?
Как найти объем конуса ?
R — радиус основания
H — высота конуса
π ≈ 3.14
Формула объема конуса, если известны радиус и высота (V):
7. Формула объема усеченного конуса
r — радиус верхнего основания
R — радиус нижнего основания
h — высота конуса
π ≈ 3.14
Формула объема усеченного конуса, если известны — радиус нижнего основания, радиус верхнего основания и высота конуса (V ):
8. Объем правильного тетраэдра
Правильный тетраэдр — пирамида у которой все грани, равносторонние треугольники.
а — ребро тетраэдра
Формула, для расчета объема правильного тетраэдра (V):
9.
 Объем правильной четырехугольной пирамиды
Объем правильной четырехугольной пирамиды
Пирамида, у которой основание квадрат и грани равные, равнобедренные треугольники, называется правильной четырехугольной пирамидой.
a — сторона основания
h — высота пирамиды
Формула для вычисления объема правильной четырехугольной пирамиды, (V):
10. Объем правильной треугольной пирамиды
Пирамида, у которой основание равносторонний треугольник и грани равные, равнобедренные треугольники, называется правильной треугольной пирамидой.
a — сторона основания
h — высота пирамиды
Формула объема правильной треугольной пирамиды, если даны — высота и сторона основания (V):
11. Найти объем правильной пирамиды
Пирамида в основании, которой лежит правильный многоугольник и грани равные треугольники, называется правильной.
h — высота пирамиды
a — сторона основания пирамиды
n — количество сторон многоугольника в основании
Формула объема правильной пирамиды, зная высоту, сторону основания и количество этих сторон (V):
12. Расчет объема пирамиды
h — высота пирамиды
S — площадь основания ABCDE
Формула для вычисления объема пирамиды, если даны — высота и площадь основания (V):
13. Расчёт объёма усечённой пирамиды
h — высота пирамиды
Sниж — площадь нижнего основания, ABCDE
Sверх — площадь верхнего основания, abcde
Формула объема усеченной пирамиды, (V):
14.
 Объем шарового сегмента, формула
Объем шарового сегмента, формула
Шаровый сегмент- это часть шара отсеченная плоскостью. В данном примере, плоскостью ABCD.
R — радиус шара
h — высота сегмента
π ≈ 3.14
Формула для расчета объема шарового сегмента, (V):
15. Объем шарового сектора
R — радиус шара
h — высота сегмента
π ≈ 3.14
Формула объема шарового сектора, (V):
16. Объем шарового слоя
h — высота шарового слоя
R — радиус нижнего основания
r — радиус верхнего основания
π ≈ 3.14
Формула объема шарового слоя, (V):
Калькулятор объема цилиндра
Автор: Ханна Памула, кандидат наук
Отзыв от Bogna Szyk и Jack Bowater
Последнее обновление: 06 сентября 2022 г.
Содержание:
- Как рассчитать объем цилиндра?
- Объем полого цилиндра
- Объем наклонного цилиндра
- Часто задаваемые вопросы
Наш калькулятор объема цилиндра позволяет вычислить объем этого твердого тела. Если вы хотите выяснить, сколько воды помещается в банку, кофе в вашу любимую кружку или даже объем соломинки для питья — вы находитесь в правильном месте. Другой вариант расчета объем цилиндрической оболочки (полый цилиндр).
Как рассчитать объем цилиндра?
Начнем с самого начала – что такое цилиндр? Это твердое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями. Мы можем представить его как твердую физическую банку с крышками сверху и снизу. Для расчета его объема нам необходимо знать два параметра – радиус (или диаметр) и высоту:
объем цилиндра = π × радиус цилиндра² × высота цилиндра
Калькулятор объема цилиндра помогает найти объем прямого, полого и наклонного цилиндра:
Объем полого цилиндра
Полый цилиндр, также называемый цилиндрической оболочкой, представляет собой трехмерную область, ограниченную двумя прямыми круговыми цилиндрами. с одной осью и двумя параллельными кольцевыми основаниями, перпендикулярными общей оси цилиндров.
с одной осью и двумя параллельными кольцевыми основаниями, перпендикулярными общей оси цилиндров.
Легче понять это определение, представив, например, соломинку для питья или трубку – полый цилиндр – это пластик, металл или другой материал. Формула объема полого цилиндра:
объем_цилиндра = π × (R² - r²) × высота_цилиндра
где R – внешний радиус, а r – внутренний радиус
Для расчета объема цилиндрической оболочки возьмем пример из реальной жизни. , может… рулон туалетной бумаги, а почему бы и нет? 😀
Введите внешний радиус цилиндра . Стандарт равен примерно 5,5 см.
Определить внутренний радиус цилиндра . Это внутренний радиус картонной детали около 2 см.
Узнать высоту цилиндра ; для нас это 9 см.
Тадаам! Объем полого цилиндра равен 742,2 см³.
Помните, что результатом является объем бумаги и картона.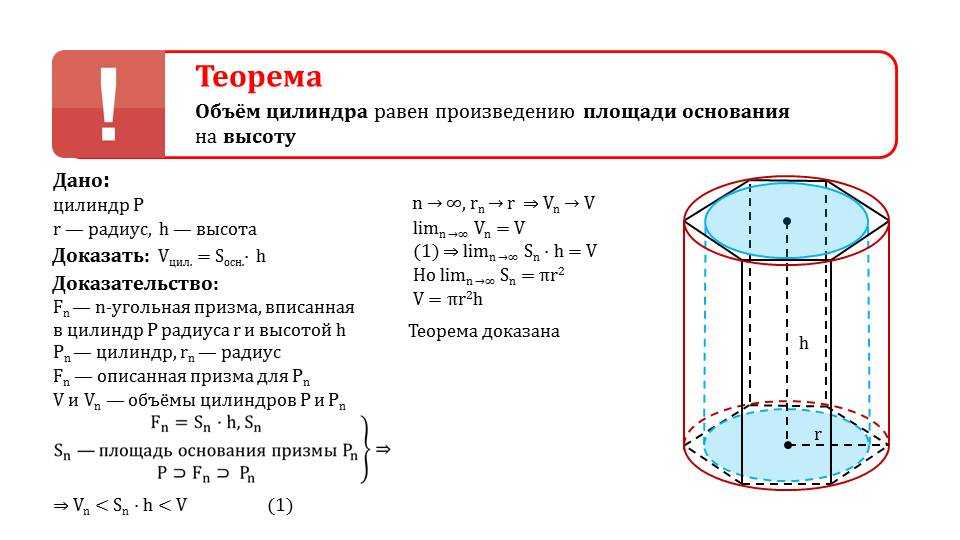 Если вы хотите посчитать, сколько пластилина можно положить внутрь картонного рулона, воспользуйтесь стандартной формулой объема цилиндра — калькулятор посчитает в мгновение ока!
Если вы хотите посчитать, сколько пластилина можно положить внутрь картонного рулона, воспользуйтесь стандартной формулой объема цилиндра — калькулятор посчитает в мгновение ока!
Объем косого цилиндра
Косой цилиндр – это тот, который «наклоняется» – стороны не перпендикулярны основаниям, в отличие от стандартного «прямого цилиндра». Как рассчитать объем косого цилиндра? Формула такая же, как и для прямого. Только помните, что высота должна быть перпендикулярна основаниям.
Теперь, когда вы знаете, как рассчитать объем цилиндра, возможно, вы захотите определить объемы других трехмерных тел? Используйте этот общий калькулятор объема!
Если вам интересно, сколько чайных ложек или чашек поместится в ваш контейнер, воспользуйтесь нашим конвертером объема.
Для расчета объема грунта, необходимого для цветочных горшков различной формы, в том числе для цилиндрического, воспользуйтесь калькулятором грунта.
Часто задаваемые вопросы
Где можно найти цилиндры в природе?
Цилиндры вокруг нас , и мы говорим не только о банках Pringles.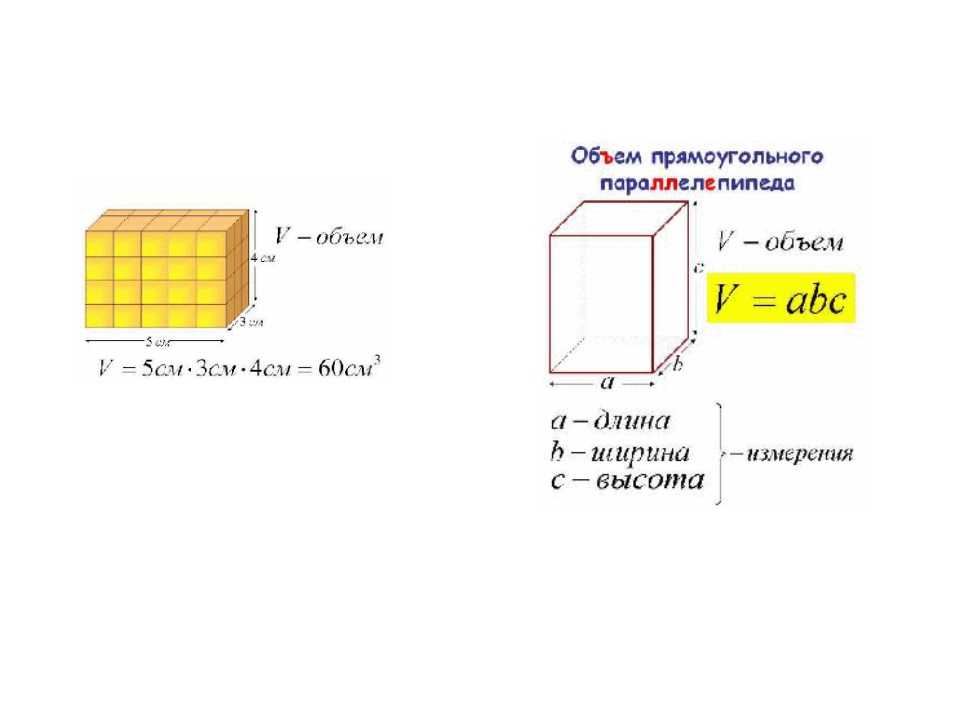 Хотя вещи в природе редко бывают идеальными цилиндрами, некоторые примеры стволы деревьев и стебли растений, некоторые кости (и, следовательно, тела) и жгутики микроскопических организмов. Они составляют большое количество природных объектов на Земле!
Хотя вещи в природе редко бывают идеальными цилиндрами, некоторые примеры стволы деревьев и стебли растений, некоторые кости (и, следовательно, тела) и жгутики микроскопических организмов. Они составляют большое количество природных объектов на Земле!
Как нарисовать цилиндр?
Чтобы нарисовать цилиндр, выполните следующие действия:
Нарисуйте слегка приплюснутый круг. Чем более он сплющен, тем ближе вы смотрите на сторону цилиндра на .
Начертить две равные параллельные линии с дальних сторон вашего круга спускается вниз.
Соедините концы двух линий полукруглой линией, которая выглядит так же, как нижняя половина вашего верхнего круга.
При необходимости добавьте тень и штриховку.
Как рассчитать вес цилиндра?
Для расчета веса баллона:
Возведение в квадрат радиуса цилиндра .

Умножьте квадрат радиуса на число пи и высоту цилиндра .
Умножьте объем на плотность цилиндра. Результат – вес цилиндра.
Как рассчитать отношение площади поверхности к объему цилиндра?
Найдите объем цилиндра по формуле πr²h .
Найдите площадь поверхности цилиндра по формуле 2πrh + 2πr² .
Из двух формул составьте отношение , т. е. πr²h : 2πrh + 2πr².
В качестве альтернативы упростите его до rh : 2(h+r) .
Разделите с обеих сторон на одну из сторон, чтобы получить соотношение в его простейшей форме.
Как найти высоту цилиндра?
Если у вас объем и радиус цилиндра:
- Убедитесь, что объем и радиус указаны в тех же единицах , что и (например, см³ и см), а радиус — в радианах .

- Квадрат радиус.
- Разделите объем на квадрат радиуса и пи, чтобы получить высоту в тех же единицах, что и радиус.
Если у вас есть площадь поверхности и радиус (r):
- Убедитесь, что поверхность и радиус указаны в тех же единицах , что и , а радиус указан в радианах.
- Вычтите 2πr² из площади поверхности.
- Разделите результат шага 1 на 2πr.
- Результат — высота цилиндра.
Как найти радиус цилиндра?
Если у вас есть объем и высота цилиндра:
- Убедитесь, что объем и высота указаны в в тех же единицах (например, см³ и см), а радиус указан в радианах .
- Разделить объем на пи и высоту.
- Квадрат корень результата.
Если у вас есть площадь поверхности и высота (h):
- Подставьте высоту, h и площадь поверхности в уравнение, площадь поверхности = πr²h : 2πrh + 2πr².

- Разделите с обеих сторон на 2π.
- Вычтите площади поверхности/2π с обеих сторон.
- Решите полученное квадратное уравнение.
- положительный корень — это радиус.
Как найти объем прямоугольного трапециевидного цилиндра?
Правильный трапециевидный цилиндр, также известный как прямоугольная призма , может быть решен следующим образом:
- Сложите вместе две параллельные стороны (основания) трапеции.
- Разделить результат на 2.
- Умножьте результат шага 2 на высоту трапеции (т.е. расстояние, разделяющее две стороны).
- Умножьте результат на длину цилиндра.
- Результатом является площадь правильного трапециевидного цилиндра.
Как найти объем овального цилиндра?
Чтобы найти объем овального цилиндра:
- Умножьте наименьший радиус овала (малая ось) на его наибольший радиус (большая ось).

- Умножьте это новое число на пи .
- Разделите результат шага 2 на 4. Результатом будет площадь овала.
- Умножьте площадь овала на высоту цилиндра.
- Результат — объем овального цилиндра.
Как найти объем наклонного цилиндра?
Чтобы вычислить объем наклонного цилиндра:
- Найдите радиус , длину стороны и угол наклона цилиндра.
- Квадрат радиус.
- Умножьте на число пи.
- Возьмем грех угла .
- Умножьте sin на длину стороны.
- Умножьте на результат шагов 3 и 5 вместе.
- В результате получается наклонный объем.
Как рассчитать рабочий объем цилиндра?
Чтобы вычислить рабочий объем цилиндра:
- Разделите диаметр отверстия на на 2, чтобы получить радиус отверстия .

- Квадрат радиус отверстия.
- Умножьте радиус квадрата на число пи.
- Умножьте результат шага 3 на длину штриха . Убедитесь, что единицы измерения диаметра и длины хода совпадают.
- Результатом является рабочий объем одного цилиндра.
Ханна Памула, кандидат наук
Правый/наклонный полный цилиндр
Высота
Радиус
Диаметр
Том
Полый цилиндр
Высота
Диаметр Внешний
Внутренний
Том
Проверьте 20 аналогичных калькуляторов геометрии 📦
Область Hemispherecubecubecubecubecubecubecubecubecubecubecubecubecubecubecubecubecubecubecubecubecubecubecubecubecubecubecubecubecububube. … еще 17
Расчет объема
Расчет объема
ДЕП | Вода/сточные воды Возврат | ||||||||||
Формула: Д х Ш *** Кубический | Объем Пожалуйста
| ||||||||||
Формула: 3. **** Кубический | Объем
|




 1417
1417