Удельное электрическое сопротивление. Формула удельное электрическое сопротивление
Удельное электрическое сопротивление — Википедия
Уде́льное электри́ческое сопротивле́ние, или просто удельное сопротивление вещества — физическая величина, характеризующая способность вещества препятствовать прохождению электрического тока.
Удельное сопротивление обозначается греческой буквой ρ. Величина, обратная удельному сопротивлению, называется удельной проводимостью (удельной электропроводностью). В отличие от электрического сопротивления, являющегося свойством проводника и зависящего от его материала, формы и размеров, удельное электрическое сопротивление является свойством только вещества.
Электрическое сопротивление однородного проводника с удельным сопротивлением ρ, длиной l и площадью поперечного сечения S может быть рассчитано по формуле R=ρ⋅lS{\displaystyle R={\frac {\rho \cdot l}{S}}} (при этом предполагается, что ни площадь, ни форма поперечного сечения не меняются вдоль проводника). Соответственно, для ρ выполняется ρ=R⋅Sl.{\displaystyle \rho ={\frac {R\cdot S}{l}}.}
Из последней формулы следует: физический смысл удельного сопротивления вещества заключается в том, что оно представляет собой сопротивление изготовленного из этого вещества однородного проводника единичной длины и с единичной площадью поперечного сечения.
Единицы измерения
Единица измерения удельного сопротивления в Международной системе единиц (СИ) — Ом·м[1]. Из соотношения ρ=R⋅Sl{\displaystyle \rho ={\frac {R\cdot S}{l}}} следует, что единица измерения удельного сопротивления в системе СИ равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 м², изготовленный из этого вещества, имеет сопротивление, равное 1 Ом[2]. Соответственно, удельное сопротивление произвольного вещества, выраженное в единицах СИ, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 м².
В технике также применяется устаревшая внесистемная единица Ом·мм²/м, равная 10−6 от 1 Ом·м[1]. Данная единица равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 мм², изготовленный из этого вещества, имеет сопротивление, равное 1 Ом[2]. Соответственно, удельное сопротивление какого-либо вещества, выраженное в этих единицах, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 мм².
Видео по теме
Обобщение понятия удельного сопротивления
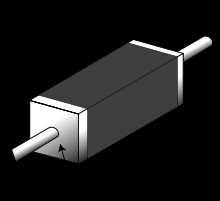Кусок резистивного материала с электрическими контактами на обоих концах Удельное сопротивление можно определить также для неоднородного материала, свойства которого меняются от точки к точке. В этом случае оно является не константой, а скалярной функцией координат — коэффициентом, связывающим напряжённость электрического поля E→(r→){\displaystyle {\vec {E}}({\vec {r}})} и плотность тока J→(r→){\displaystyle {\vec {J}}({\vec {r}})} в данной точке r→{\displaystyle {\vec {r}}}. Указанная связь выражается законом Ома в дифференциальной форме:
Эта формула справедлива для неоднородного, но изотропного вещества. Вещество может быть и анизотропно (большинство кристаллов, намагниченная плазма и т. д.), то есть его свойства могут зависеть от направления. В этом случае удельное сопротивление является зависящим от координат тензором второго ранга, содержащим девять компонент ρij{\displaystyle \rho _{ij}}. В анизотропном веществе векторы плотности тока и напряжённости электрического поля в каждой данной точке вещества не сонаправлены; связь между ними выражается соотношением
Ei(r→)=∑j=13ρij(r→)Jj(r→).{\displaystyle E_{i}({\vec {r}})=\sum _{j=1}^{3}\rho _{ij}({\vec {r}})J_{j}({\vec {r}}).}В анизотропном, но однородном веществе тензор ρij{\displaystyle \rho _{ij}} от координат не зависит.
Тензор ρij{\displaystyle \rho _{ij}} симметричен, то есть для любых i{\displaystyle i} и j{\displaystyle j} выполняется ρij=ρji{\displaystyle \rho _{ij}=\rho _{ji}}.
Как и для всякого симметричного тензора, для ρij{\displaystyle \rho _{ij}} можно выбрать ортогональную систему декартовых координат, в которых матрица ρij{\displaystyle \rho _{ij}} становится диагональной, то есть приобретает вид, при котором из девяти компонент ρij{\displaystyle \rho _{ij}} отличными от нуля являются лишь три: ρ11{\displaystyle \rho _{11}}, ρ22{\displaystyle \rho _{22}} и ρ33{\displaystyle \rho _{33}}. В этом случае, обозначив ρii{\displaystyle \rho _{ii}} как ρi{\displaystyle \rho _{i}}, вместо предыдущей формулы получаем более простую
Ei=ρiJi.{\displaystyle E_{i}=\rho _{i}J_{i}.}Величины ρi{\displaystyle \rho _{i}} называют главными значениями тензора удельного сопротивления.
Связь с удельной проводимостью
В изотропных материалах связь между удельным сопротивлением ρ{\displaystyle \rho } и удельной проводимостью σ{\displaystyle \sigma } выражается равенством
ρ=1σ.{\displaystyle \rho ={\frac {1}{\sigma }}.}В случае анизотропных материалов связь между компонентами тензора удельного сопротивления ρij{\displaystyle \rho _{ij}} и тензора удельной проводимости σij{\displaystyle \sigma _{ij}} имеет более сложный характер. Действительно, закон Ома в дифференциальной форме для анизотропных материалов имеет вид:
Ji(r→)=∑j=13σij(r→)Ej(r→).{\displaystyle J_{i}({\vec {r}})=\sum _{j=1}^{3}\sigma _{ij}({\vec {r}})E_{j}({\vec {r}}).}Из этого равенства и приведённого ранее соотношения для Ei(r→){\displaystyle E_{i}({\vec {r}})} следует, что тензор удельного сопротивления является обратным тензору удельной проводимости. С учётом этого для компонент тензора удельного сопротивления выполняется:
ρ11=1det(σ)[σ22σ33−σ23σ32],{\displaystyle \rho _{11}={\frac {1}{\det(\sigma )}}[\sigma _{22}\sigma _{33}-\sigma _{23}\sigma _{32}],}ρ12=1det(σ)[σ33σ12−σ13σ32],{\displaystyle \rho _{12}={\frac {1}{\det(\sigma )}}[\sigma _{33}\sigma _{12}-\sigma _{13}\sigma _{32}],}где det(σ){\displaystyle \det(\sigma )} — определитель матрицы, составленной из компонент тензора σij{\displaystyle \sigma _{ij}}. Остальные компоненты тензора удельного сопротивления получаются из приведённых уравнений в результате циклической перестановки индексов 1, 2 и 3[3].
Удельное электрическое сопротивление некоторых веществ
Металлические монокристаллы
В таблице приведены главные значения тензора удельного сопротивления монокристаллов при температуре 20 °C[4].
| Олово | 9,9 | 14,3 |
| Висмут | 109 | 138 |
| Кадмий | 6,8 | 8,3 |
| Цинк | 5,91 | 6,13 |
| Теллур | 2,90·109 | 5,9·109 |
Металлы и сплавы, применяемые в электротехнике
Разброс значений обусловлен разной химической чистотой металлов, способов изготовления образцов, изученных разными учеными и непостоянством состава сплавов.
|
|
Значения даны при температуре t = 20 °C. Сопротивления сплавов зависят от их химического состава и могут варьироваться. Для чистых веществ колебания численных значений удельного сопротивления обусловлены различными методами механической и термической обработки, например, отжигом проволоки после волочения.
Другие вещества
Тонкие плёнки
Сопротивление тонких плоских плёнок (когда её толщина много меньше расстояния между контактами) принято называть «удельным сопротивлением на квадрат», RSq.{\displaystyle R_{\mathrm {Sq} }.} Этот параметр удобен тем, что сопротивление квадратного куска проводящей плёнки не зависит от размеров этого квадрата, при приложении напряжения по противоположным сторонам квадрата. При этом сопротивление куска плёнки, если он имеет форму прямоугольника, не зависит от его линейных размеров, а только от отношения длины (измеренной вдоль линий тока) к его ширине L/W: RSq=RW/L,{\displaystyle R_{\mathrm {Sq} }=RW/L,} где R — измеренное сопротивление. В общем случае, если форма образца отличается от прямоугольной, и поле в пленке неоднородное, используют метод ван дер Пау.
Примечания
- ↑ 1 2 Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 93. — 240 с. — ISBN 5-7050-0118-5.
- ↑ 1 2 Чертов А. Г. Единицы физических величин. — М.: «Высшая школа», 1977. — 287 с.
- ↑ Давыдов А. С. Теория твёрдого тела. — М.: «Наука», 1976. — С. 191—192. — 646 с.
- ↑ Шувалов Л. А. и др. Физические свойства кристаллов // Современная кристаллография / Гл. ред. Б. К. Вайнштейн. — М.: «Наука», 1981. — Т. 4. — С. 317.
См. также
wikipedia.green
Закон Ома и удельное электрическое сопротивление - формулы и определения
2016 г. Справочники - Мобильная версия - Электротехника
Памятка по электротехнике
Закон Ома устанавливает связь между силой тока в проводнике и разностью потенциалов (напряжением) на его концах. Формулировка для участка электрической цепи (проводника), не содержащего источников электродвижущей силы (ЭДС): сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению проводника. Законы Ома для замкнутой неразветвлённой цепи: сила тока прямо пропорциональна электродвижущей силе и обратно пропорциональна полному сопротивлению цепи. Закон Ома справедлив для постоянных и квазистационарных токов. Был открыт немецким физиком Георгом Омом в 1826 году. * Современная энциклопедия
В случае переменного тока, величины, входящие в расчётные формулы – становятся комплексными.
Закон Ома в дифференциальной форме - описывает исключительно электропроводящие свойства материала, вне зависимости от геометрических размеров.
Удельное электрическое сопротивление вещества есть электросопротивление изготовленного из него куба со сторонами, равными единице (1метр), когда ток идёт перпендикулярно двум его противоположным граням, площадью 1 квадратный метр каждая.
Удельное сопротивление зависит от концентрации в проводнике свободных электронов и от расстояния между ионами кристаллической решетки, иначе говоря, от материала проводника.
Размерность удельного электросопротивления в сист. СИ (международная система единиц, англ. - International System of Units) – Ом·м [Ом*м^2/м] (SI – Ω·m, рус. – Ом-метр, англ. – ohm-meter). Для измерения проводниковых материалов разрешается использовать внесистемную единицу – Ом·мм2/м (для миллиметрового сечения проводника, длиной 1 м. то есть – миллионную часть Ом-метра).
Физический смысл удельного сопротивления: материал (однородный и изотропный*) имеет удельное электрическое сопротивление один Ом·м, если изготовленный из этого материала куб со стороной 1 метр имеет сопротивление 1 Ом при измерении на противоположных гранях куба. * Изотропность – идентичность физических свойств во всех направлениях.
Удельное сопротивление характеризует способность вещества проводить электрический ток и не зависит от формы и размеров вещества, но меняется, при отличии его температуры от 20 °C (то есть, от комнатной, при которой определялись табличные значения для справочников).
На практике, в технике чаще применяется единица, в миллион раз меньшая (миллиметровое токоведущее сечение), чем Ом·м:
1 мкОм·м (SI – µΩ·m, рус. – микроом-метр, англ. – microhm-meter) = 1*10^-6 Ом*м 1 мкОм·м = 1 Ом·мм2/м
При этом, удельное сопротивление однородного куска проводника длиной 1 метр и площадью токоведущего сечения 1 квадратный миллиметр – равно 1 Ом·мм2/м, если его сополтивление равно 1 Ом. Например, величина удельного сопротивления электротехнической меди, примерно, составляет 1,72*10^-8 Ом·м = 0.0172 мкОм·м (определяется при температуре 20 градусов по Цельсию).
В зависимости от удельного сопротивления все вещества делятся на проводники, диэлектрики и полупроводники. Диэлектрики (изоляторы, например - фарфор) имеют очень высокие значения удельного электрического сопротивления, превышающие 10^12 Ом·м, а проводники (к примеру - серебро, медь) – меньше 10^-2 Ом·м ( R = (R1 * (1 + α * (t2–t1))) * L / S = = 2,62*10 -8 Ом•м * (1 + 0,0042*95) * 100 / (3,14 * 40 2 * 10 -6 ) = 7,3 * 10 -4 Ом где:S – площадь сечения в м 2 (с вычетом толщины слоёв изоляции), L – длина проводника в метрах.
Температурный коэффициент сопротивления х10 -3. 1/градус:Алюминий – 4,2 Бронза оловянистая твёрдотянутая – 0,6-0,7 Вольфрам – 4,2 Графит – -1,3 Дюраль – 2,2 Константан – 0,003-0,005 Латунь – 1,5 Манганин – 0,03-0,06 (при температуре до 250-300°С) Медь – 4,3 Нихром – 0,14 Серебро – 4,0 Сталь – 9,0 Цинк – 4,2
Постоянные резисторы и их маркировка
В буквенно-цифровой (кодовой) маркировке резисторов – на их корпус наносится числовое значение электрического сопротивления и буквы, первая из которых обозначает множитель (R или Е – Ом,  K – килоом,  M – мегаом) и, заодно, определяет положение разделительной запятой десятичного знака. Вторая буква означает класс точности, то есть, допускаемое отклонение от указанной величины. Номиналы на мелкие детали – наносят в виде маркировки цветными кольцами, полосками или точками (в зависимости от применяемого стандарта). Каждому цвету соответствует определенная цифра, означающая число Ом, множитель / степень или процент точности. Для быстрого определения номинала резистора по цветовой кодировке, применяются специальные компьютерные программы. Читать дальше.
Пример расчёта, на основе школьной задачки по физике из программы 9 класса.
Задание: определить (найти в таблице), по известному удельному сопротивлению p = 0.017Ом·мм2/м - какой это материал? Рассчитать диаметр проволоки. Вычислить электрическое сопротивление провода, длиной L = 80 см, сечением S = 0.2 мм2 Решение задачи: По таблице определяем, что удельное сопротивление, равное 0.017 Ом·мм2/м может быть у меди.
Из формулы S = 3.1416 * (радиус)^2 = 3.142 * ((диаметр)^2)/4 с помощью своего калькулятора, находится диаметр (в миллиметрах) = корень квадратный из (4 * S / 3.14)
Длина провода, в единицах системы СИ (переводим в метры): 80 см = 0.8 м
Находим электр. сопротивление по формуле: R = (p * L) / S = (0.017 * 0.8) / 0.2 = 0.068 Ом
Ответ: с точностью до второго знака после запятой, R = 0.07 Ом
О р е н б у р г с к и е п л а т к и, п а л а н т и н ы, ш а р ф ы, к а р д и г а н ы, ш а л и
Справки больничные листы работника, образец больничного листа посмотреть. | Электромонтажные работы - монтаж электрики, подключение и обслуживание электропроводки. | Минисправочник по электрическим параметрам. соотношения Ом х мм2/м и мкОм x м (микроом), в технических расчётах.
Copyright © 2007-2016, KAKRAS.RU
http://www.kakras.ru
legkoe-delo.ru
5. Удельное электрическое сопротивление | 11. Физика проводников и диэлектриков | Часть1
5. Удельное электрическое сопротивление
Удельное электрическое сопротивление
Величина допустимой токовой нагрузки на провода является грубой оценкой их сопротивления, основывающейся на способности тока нагревать эти провода до высокой температуры. Иногда мы сталкиваемся с такими ситуациями, в которых падение напряжения, созданное сопротивлением проводов, создает нам совершенно иные проблемы (не связанные с нагревом). Например, у нас может быть схема, для которой величина напряжения является критической, и не должна падать ниже определенного значения:
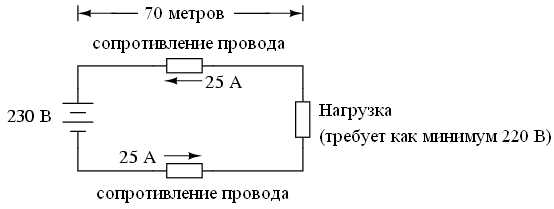
Напряжение источника питания данной схемы составляет 230 В, а для питания нагрузки требуется как минимум 220 В. Отсюда можно сделать вывод, что потери напряжения на проводах не должны превышать 10 В. Так как проводов у нас два, то делим 10 вольт на 2 и получаем по 5 вольт допустимых потерь напряжения на каждый провод. Используя Закон Ома (R = U / I), мы можем рассчитать максимально допустимое сопротивление каждого провода:
Нам известно, что длина каждого из проводов равна 70 метрам, но как мы сможем рассчитать реальное сопротивление конкретных проводов определенного размера и дины? В этом нам поможет следующая формула:
Данная формула соотносит сопротивление проводника с его удельным сопротивлением (греческая буква "ро" ρ), длиной (l) и площадью поперечного сечения (S). Из этой формулы видно, что сопротивление провода возрастет при увеличении его длины (аналогия: жидкости труднее течь по длинной трубе, чем по короткой), и уменьшится при увеличении площади поперечного сечения (аналогия: жидкости легче течь по толстой трубе, чем по тонкой). Удельное сопротивление является постоянной величиной для конкретного типа материала, из которого изготовлен провод.
Удельные сопротивления некоторых проводящих материалов можно найти в нижеприведенной таблице. Из этой таблицы видно, что хорошим проводником является медь, по проводимости она уступает только серебру.
| Металл | ρ, Ом·мм2/м |
| Серебро | 0,016 |
| Медь | 0,0175 |
| Золото | 0,023 |
| Алюминий | 0,0271 |
| Иридий | 0,0474 |
| Молибден | 0,054 |
| Вольфрам | 0,055 |
| Цинк | 0,059 |
| Никель | 0,087 |
| Железо | 0,098 |
| Платина | 0,107 |
| Олово | 0,12 |
| Свинец | 0,205 |
| Титан | 0,5562 - 0,7837 |
| Висмут | 1,2 |
| Сплав | ρ, Ом·мм2/м |
| Сталь | 0,1400 |
| Никелин | 0,42 |
| Константан | 0,5 |
| Манганин | 0,43…0,51 |
| Нихром | 1,05…1,4 |
| Фехраль | 1,15…1,35 |
| Хромаль | 1,3…1,5 |
| Латунь | 0,07…0,08 |
Значения здесь даны при температуре t = 20° C. Сопротивления сплавов зависят от их точного состава и могут варьироваться.
Обратите внимание на приведенную в таблице единицу измерения удельного сопротивления (Ом·мм2/м). Она говорит нам о том, что в формуле R=ρl/S нужно использовать длину в метрах, а площадь поперечного сечения в квадратных миллиметрах.
Давайте вернемся к нашему примеру, в котором мы подбираем провод, обладающий сопротивлением 0,2 Ом или менее на длине 70 метров. Предполагая, что будет использоваться медный провод (самый распространенный тип электрических проводов), можно преобразовать последнюю формулу в следующий вид:
Таким образом, в нашем случае достаточно будет медного провода сечением 6,125 мм2. Допустимая токовая нагрузка такого провода выше заявленных в схеме 25 А.
www.radiomexanik.spb.ru
Удельное электрическое сопротивление - это... Что такое Удельное электрическое сопротивление?
Удельное электрическое сопротивление, или просто удельное сопротивление вещества характеризует его способность препятствовать прохождению электрического тока.
Единица измерения удельного сопротивления в Международной системе единиц (СИ) — Ом·м; также измеряется в Ом·см и Ом·мм²/м. Физический смысл удельного сопротивления в СИ: сопротивление однородного куска проводника длиной 1 м и площадью токоведущего сечения 1 м².
В технике часто применяется в миллион раз меньшая производная единица: Ом·мм²/м, равная 10−6 от 1 Ом·м: 1 Ом·м = 1·106 Ом·мм²/м. Физический смысл удельного сопротивления в технике: сопротивление однородного куска проводника длиной 1 м и площадью токоведущего сечения 1 кв.мм.
Величина удельного сопротивления обозначается греческой буквой .
Сопротивление проводника с удельным сопротивлением , длиной и площадью сечения может быть рассчитано по формуле
Обобщение понятия удельного сопротивления
Удельное сопротивление можно определить также для неоднородного материала, свойства которого меняются от точки к точке. В этом случае оно является не константой, а скалярной функцией — коэффициентом, связывающим напряжённость электрического поля и плотность тока в данной точке
Эта формула справедлива для неоднородного, но изотропного вещества. Вещество может быть и анизотропно (большинство кристаллов, намагниченная плазма и т. д.), то есть его свойства зависят от направления (вообще говоря, в нём векторы тока и напряжённости электрического поля в данной точке не сонаправлены). В этом случае удельное сопротивление является зависящим от координат тензором второго ранга:
Удельное электрическое сопротивление металлов и сплавов, применяемых в электротехнике
|
|
Значения даны при температуре t = 20° C. Сопротивления сплавов зависят от их точного состава и могут варьироваться.
Тонкие плёнки
Удельное сопротивление в тонких плёнках (когда толщина образца много меньше расстояния между контактами) характеризуется «удельным сопротивлением на квадрат», . В этом случае удельное сопротивление не зависит от линейных размеров образца если он имеет форму прямоугольника, а только от отношения (длины к ширине) L/W: , где R - измеренное сопротивление. В случае если форма образца отличается от прямоугольной используют метод ван дер Пау.
См. также
Ссылки
dal.academic.ru
Удельное электрическое сопротивление - это... Что такое Удельное электрическое сопротивление?
Удельное электрическое сопротивление, или просто удельное сопротивление вещества характеризует его способность препятствовать прохождению электрического тока.
Единица измерения удельного сопротивления в Международной системе единиц (СИ) — Ом·м; также измеряется в Ом·см и Ом·мм²/м. Физический смысл удельного сопротивления в СИ: сопротивление однородного куска проводника длиной 1 м и площадью токоведущего сечения 1 м².
В технике часто применяется в миллион раз меньшая производная единица: Ом·мм²/м, равная 10−6 от 1 Ом·м: 1 Ом·м = 1·106 Ом·мм²/м. Физический смысл удельного сопротивления в технике: сопротивление однородного куска проводника длиной 1 м и площадью токоведущего сечения 1 кв.мм.
Величина удельного сопротивления обозначается греческой буквой .
Сопротивление проводника с удельным сопротивлением , длиной и площадью сечения может быть рассчитано по формуле
Обобщение понятия удельного сопротивления
Удельное сопротивление можно определить также для неоднородного материала, свойства которого меняются от точки к точке. В этом случае оно является не константой, а скалярной функцией — коэффициентом, связывающим напряжённость электрического поля и плотность тока в данной точке
Эта формула справедлива для неоднородного, но изотропного вещества. Вещество может быть и анизотропно (большинство кристаллов, намагниченная плазма и т. д.), то есть его свойства зависят от направления (вообще говоря, в нём векторы тока и напряжённости электрического поля в данной точке не сонаправлены). В этом случае удельное сопротивление является зависящим от координат тензором второго ранга:
Удельное электрическое сопротивление металлов и сплавов, применяемых в электротехнике
|
|
Значения даны при температуре t = 20° C. Сопротивления сплавов зависят от их точного состава и могут варьироваться.
Тонкие плёнки
Удельное сопротивление в тонких плёнках (когда толщина образца много меньше расстояния между контактами) характеризуется «удельным сопротивлением на квадрат», . В этом случае удельное сопротивление не зависит от линейных размеров образца если он имеет форму прямоугольника, а только от отношения (длины к ширине) L/W: , где R - измеренное сопротивление. В случае если форма образца отличается от прямоугольной используют метод ван дер Пау.
См. также
Ссылки
dik.academic.ru
Удельное электрическое сопротивление - Gpedia, Your Encyclopedia
Уде́льное электри́ческое сопротивле́ние, или просто удельное сопротивление вещества — физическая величина, характеризующая способность вещества препятствовать прохождению электрического тока.
Удельное сопротивление обозначается греческой буквой ρ. Величина, обратная удельному сопротивлению, называется удельной проводимостью (удельной электропроводностью). В отличие от электрического сопротивления, являющегося свойством проводника и зависящего от его материала, формы и размеров, удельное электрическое сопротивление является свойством только вещества.
Электрическое сопротивление однородного проводника с удельным сопротивлением ρ, длиной l и площадью поперечного сечения S может быть рассчитано по формуле R=ρ⋅lS{\displaystyle R={\frac {\rho \cdot l}{S}}} (при этом предполагается, что ни площадь, ни форма поперечного сечения не меняются вдоль проводника). Соответственно, для ρ выполняется ρ=R⋅Sl.{\displaystyle \rho ={\frac {R\cdot S}{l}}.}
Из последней формулы следует: физический смысл удельного сопротивления вещества заключается в том, что оно представляет собой сопротивление изготовленного из этого вещества однородного проводника единичной длины и с единичной площадью поперечного сечения.
Единицы измерения
Единица измерения удельного сопротивления в Международной системе единиц (СИ) — Ом·м[1]. Из соотношения ρ=R⋅Sl{\displaystyle \rho ={\frac {R\cdot S}{l}}} следует, что единица измерения удельного сопротивления в системе СИ равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 м², изготовленный из этого вещества, имеет сопротивление, равное 1 Ом[2]. Соответственно, удельное сопротивление произвольного вещества, выраженное в единицах СИ, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 м².
В технике также применяется устаревшая внесистемная единица Ом·мм²/м, равная 10−6 от 1 Ом·м[1]. Данная единица равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 мм², изготовленный из этого вещества, имеет сопротивление, равное 1 Ом[2]. Соответственно, удельное сопротивление какого-либо вещества, выраженное в этих единицах, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 мм².
Обобщение понятия удельного сопротивления
Кусок резистивного материала с электрическими контактами на обоих концах Удельное сопротивление можно определить также для неоднородного материала, свойства которого меняются от точки к точке. В этом случае оно является не константой, а скалярной функцией координат — коэффициентом, связывающим напряжённость электрического поля E→(r→){\displaystyle {\vec {E}}({\vec {r}})} и плотность тока J→(r→){\displaystyle {\vec {J}}({\vec {r}})} в данной точке r→{\displaystyle {\vec {r}}}. Указанная связь выражается законом Ома в дифференциальной форме:
E→(r→)=ρ(r→)J→(r→).{\displaystyle {\vec {E}}({\vec {r}})=\rho ({\vec {r}}){\vec {J}}({\vec {r}}).}Эта формула справедлива для неоднородного, но изотропного вещества. Вещество может быть и анизотропно (большинство кристаллов, намагниченная плазма и т. д.), то есть его свойства могут зависеть от направления. В этом случае удельное сопротивление является зависящим от координат тензором второго ранга, содержащим девять компонент ρij{\displaystyle \rho _{ij}}. В анизотропном веществе векторы плотности тока и напряжённости электрического поля в каждой данной точке вещества не сонаправлены; связь между ними выражается соотношением
Ei(r→)=∑j=13ρij(r→)Jj(r→).{\displaystyle E_{i}({\vec {r}})=\sum _{j=1}^{3}\rho _{ij}({\vec {r}})J_{j}({\vec {r}}).}В анизотропном, но однородном веществе тензор ρij{\displaystyle \rho _{ij}} от координат не зависит.
Тензор ρij{\displaystyle \rho _{ij}} симметричен, то есть для любых i{\displaystyle i} и j{\displaystyle j} выполняется ρij=ρji{\displaystyle \rho _{ij}=\rho _{ji}}.
Как и для всякого симметричного тензора, для ρij{\displaystyle \rho _{ij}} можно выбрать ортогональную систему декартовых координат, в которых матрица ρij{\displaystyle \rho _{ij}} становится диагональной, то есть приобретает вид, при котором из девяти компонент ρij{\displaystyle \rho _{ij}} отличными от нуля являются лишь три: ρ11{\displaystyle \rho _{11}}, ρ22{\displaystyle \rho _{22}} и ρ33{\displaystyle \rho _{33}}. В этом случае, обозначив ρii{\displaystyle \rho _{ii}} как ρi{\displaystyle \rho _{i}}, вместо предыдущей формулы получаем более простую
Ei=ρiJi.{\displaystyle E_{i}=\rho _{i}J_{i}.}Величины ρi{\displaystyle \rho _{i}} называют главными значениями тензора удельного сопротивления.
Связь с удельной проводимостью
В изотропных материалах связь между удельным сопротивлением ρ{\displaystyle \rho } и удельной проводимостью σ{\displaystyle \sigma } выражается равенством
ρ=1σ.{\displaystyle \rho ={\frac {1}{\sigma }}.}В случае анизотропных материалов связь между компонентами тензора удельного сопротивления ρij{\displaystyle \rho _{ij}} и тензора удельной проводимости σij{\displaystyle \sigma _{ij}} имеет более сложный характер. Действительно, закон Ома в дифференциальной форме для анизотропных материалов имеет вид:
Ji(r→)=∑j=13σij(r→)Ej(r→).{\displaystyle J_{i}({\vec {r}})=\sum _{j=1}^{3}\sigma _{ij}({\vec {r}})E_{j}({\vec {r}}).}Из этого равенства и приведённого ранее соотношения для Ei(r→){\displaystyle E_{i}({\vec {r}})} следует, что тензор удельного сопротивления является обратным тензору удельной проводимости. С учётом этого для компонент тензора удельного сопротивления выполняется:
ρ11=1det(σ)[σ22σ33−σ23σ32],{\displaystyle \rho _{11}={\frac {1}{\det(\sigma )}}[\sigma _{22}\sigma _{33}-\sigma _{23}\sigma _{32}],}ρ12=1det(σ)[σ33σ12−σ13σ32],{\displaystyle \rho _{12}={\frac {1}{\det(\sigma )}}[\sigma _{33}\sigma _{12}-\sigma _{13}\sigma _{32}],}где det(σ){\displaystyle \det(\sigma )} — определитель матрицы, составленной из компонент тензора σij{\displaystyle \sigma _{ij}}. Остальные компоненты тензора удельного сопротивления получаются из приведённых уравнений в результате циклической перестановки индексов 1, 2 и 3[3].
Удельное электрическое сопротивление некоторых веществ
Металлические монокристаллы
В таблице приведены главные значения тензора удельного сопротивления монокристаллов при температуре 20 °C[4].
| Олово | 9,9 | 14,3 |
| Висмут | 109 | 138 |
| Кадмий | 6,8 | 8,3 |
| Цинк | 5,91 | 6,13 |
| Теллур | 2,90·109 | 5,9·109 |
Металлы и сплавы, применяемые в электротехнике
Разброс значений обусловлен разной химической чистотой металлов, способов изготовления образцов, изученных разными учеными и непостоянством состава сплавов.
|
|
Значения даны при температуре t = 20 °C. Сопротивления сплавов зависят от их химического состава и могут варьироваться. Для чистых веществ колебания численных значений удельного сопротивления обусловлены различными методами механической и термической обработки, например, отжигом проволоки после волочения.
Другие вещества
Тонкие плёнки
Сопротивление тонких плоских плёнок (когда её толщина много меньше расстояния между контактами) принято называть «удельным сопротивлением на квадрат», RSq.{\displaystyle R_{\mathrm {Sq} }.} Этот параметр удобен тем, что сопротивление квадратного куска проводящей плёнки не зависит от размеров этого квадрата, при приложении напряжения по противоположным сторонам квадрата. При этом сопротивление куска плёнки, если он имеет форму прямоугольника, не зависит от его линейных размеров, а только от отношения длины (измеренной вдоль линий тока) к его ширине L/W: RSq=RW/L,{\displaystyle R_{\mathrm {Sq} }=RW/L,} где R — измеренное сопротивление. В общем случае, если форма образца отличается от прямоугольной, и поле в пленке неоднородное, используют метод ван дер Пау.
Примечания
- ↑ 1 2 Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 93. — 240 с. — ISBN 5-7050-0118-5.
- ↑ 1 2 Чертов А. Г. Единицы физических величин. — М.: «Высшая школа», 1977. — 287 с.
- ↑ Давыдов А. С. Теория твёрдого тела. — М.: «Наука», 1976. — С. 191—192. — 646 с.
- ↑ Шувалов Л. А. и др. Физические свойства кристаллов // Современная кристаллография / Гл. ред. Б. К. Вайнштейн. — М.: «Наука», 1981. — Т. 4. — С. 317.
См. также
www.gpedia.com
Удельное сопротивление Википедия
Уде́льное электри́ческое сопротивле́ние, или просто удельное сопротивление вещества — физическая величина, характеризующая способность вещества препятствовать прохождению электрического тока.
Удельное сопротивление обозначается греческой буквой ρ. Величина, обратная удельному сопротивлению, называется удельной проводимостью (удельной электропроводностью). В отличие от электрического сопротивления, являющегося свойством проводника и зависящего от его материала, формы и размеров, удельное электрическое сопротивление является свойством только вещества.
Электрическое сопротивление однородного проводника с удельным сопротивлением ρ, длиной l и площадью поперечного сечения S может быть рассчитано по формуле R=ρ⋅lS{\displaystyle R={\frac {\rho \cdot l}{S}}} (при этом предполагается, что ни площадь, ни форма поперечного сечения не меняются вдоль проводника). Соответственно, для ρ выполняется ρ=R⋅Sl.{\displaystyle \rho ={\frac {R\cdot S}{l}}.}
Из последней формулы следует: физический смысл удельного сопротивления вещества заключается в том, что оно представляет собой сопротивление изготовленного из этого вещества однородного проводника единичной длины и с единичной площадью поперечного сечения.
Единицы измерения[ | код]
Единица измерения удельного сопротивления в Международной системе единиц (СИ) — Ом·м[1]. Из соотношения ρ=R⋅Sl{\displaystyle \rho ={\frac {R\cdot S}{l}}} следует, что единица измерения удельного сопротивления в системе СИ равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 м², изготовленный из этого вещества, имеет сопротивление, равное 1 Ом[2]. Соответственно, удельное сопротивление произвольного вещества, выраженное в единицах СИ, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 м².
В технике также применяется устаревшая внесистемная единица Ом·мм²/м, равная 10−6 от 1 Ом·м[1]. Данная единица равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 мм², изготовленный из этого вещества, имеет сопротивление, равное 1 Ом[2]. Соответственно, удельное сопротивление какого-либо вещества, выраженное в этих единицах, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 мм².
Обобщение понятия удельного сопротивления[ | код]
ru-wiki.ru
