Содержание
формула для определения объема бревна
При покупке необработанного леса каждый кубический дециметр для нас очень важен. Особенно если мы точно рассчитали количество необходимого леса для последующего распила либо оцилиндрованных бревен. Поэтому очень важно знать точный объем поставляемого леса-кругляка.
Обмер и учет лесных материалов.
Так как пиломатериалы и поставляемый вес при расчетах учитывают в кубических метрах, то стоимость леса измеряется в денежных единицах за кубический м.
Поэтому нужно знать фактический объем древесины, которую вы заказываете или покупаете.
Этот объем, выраженный в кубических метрах, и будет кубатурой леса.
Произведение расчета кубатуры леса по кубатурнику
Пример расчет кубатуры бревна с помощью он-лаин программы.
Наиболее распространенным методом определения объема круглого бревна является использование кубатурника. Это специальная таблица расчета кубатуры. Кубатурник позволяет по длине бревна с шагом 0,5 метра и диаметру хлыста (более тонкой части бревна) определить объем данного бревна в кубических метрах с точностью до тысячных. Для этого измеряются диаметр вершины бревна и длина бревна и по ним проводят расчет кубатуры в кубатурнике. Если сечение бревна на срезе хлыста недостаточно круглое, тогда измеряется самый большой диаметр и самый малый при перпендикулярных измерениях. Из них вычисляется среднее, округляют его до ближайшего целого, по которому и ищут в кубатурнике объем бревна. Кубатурник регламентирован ГОСТ 2708-75 , ISO 4480-83 ”Лесоматериалы круглые. Таблицы объемов”.
Для этого измеряются диаметр вершины бревна и длина бревна и по ним проводят расчет кубатуры в кубатурнике. Если сечение бревна на срезе хлыста недостаточно круглое, тогда измеряется самый большой диаметр и самый малый при перпендикулярных измерениях. Из них вычисляется среднее, округляют его до ближайшего целого, по которому и ищут в кубатурнике объем бревна. Кубатурник регламентирован ГОСТ 2708-75 , ISO 4480-83 ”Лесоматериалы круглые. Таблицы объемов”.
При необходимости вычисления объема древесины в складометрах нужно вычислить объем каждого бревна и их сложить.
Если длина бревна намного больше, чем есть в кубатурнике, то вычисление кубатуры бревна производят путем сложения кубатуры двух его составляющих.
Однако этот метод вычисления довольно неточен и может привести к большой переплате за поставленный лес.
Поэтому приходится искать более точные методы вычисления объема круглого леса.
Вернуться к оглавлению
Расчет кубатуры оцилиндрованного бревна
Расчет кубатуры оцилиндрованного бревна и профилированного бруса.
Если бревна оцилиндрованные, то точный объем этого бревна можно рассчитать по формуле вычисления объема цилиндра:
V = π*D2*L/4, где
- V – кубатура бревна, м3;
- D – диаметр бревна, м;
- L – длина бревна, м;
- π – постоянная.
Но мы стремимся узнать более точный объем необработанного круглого леса, бревна которого имеют сбежистость.
Сбежистостью называют изменение диаметра круглых бревен лесоматериалов от одного конца к другому. Она измеряется в % и вычисляется делением разницы диаметров на длину, на которой эта разница обнаруживается. Нормальный сбег (сбежистость) равен 1% (1 см на 1 м длины бревна). Сбежистость увеличивает количество отходов при их распиловке и оцилиндрении бревен.
Вернуться к оглавлению
Формула расчета кубатуры леса
Таблица расчета кубатуры бревен.
В стандартном кубатурнике предусматривается некоторая сбежистость, и поэтому все данные в нем вычислены по диаметру хлыстов вершины.
Но сбежистость у разных деревьев бывают разная. Нормальная сбежистость принимается только для хвойных деревьев, и то лишь при укрупненных расчетах. Для насаждений ІІ и ІІІ бонитетов среднее значение сбежистости в промежутке диаметров бревна от 14 до 60 см колеблется от 0,8% до 1,8%.
Поэтому предлагается следующий способ более точного определения фактического объема бревна необработанного леса. Для начала измеряется диаметр бревна на вершине и его длина, а затем измеряется диаметр комля одного из наиболее характерных по сбегу бревен. На следующем этапе вычисляется сбежистость бревен – разница диаметров комля и хлыста делится на длину бревна. Например, если бревно длиной 8 м имеет диаметр на вершине в двух перпендикулярных направлениях 14 и 16 см, а диаметр среза в комлевой части 22 и 24 см, то сбежистость бревна вычисляем по формуле:
С=(D1+D2-d1- d2) / 2L, где
- d1,d2 – диаметр бревна на верхнем срезе (хлысте) соответственно по двум перпендикулярным направлениям, см;
- D1,D2 – диаметр бревна на нижнем срезе (комле) соответственно по двум перпендикулярным направлениям, см;
- L – длина бревна, м.

В нашем случае С = (22+24-16-14) см²* 8 м=1,0 см/м.
То есть для данной древесины на одном метре длины ствола его диаметр уменьшается от комля до хлыста на 1,0 см (нормальная).
При правильной окружности срезов, когда d1=d2 и D1=D2; С=(D-d) /L
Зная длину бревна и диаметр одного конца (нижнего или верхнего) по формуле вычисления, которая выведена из геометрической формулы объема усеченного конуса, определяем объем любого бревна:
V =π * (D2+D*d + d2) *L/120000, где
- d =(d1+d2)/2 – диаметр бревна на верхнем срезе (хлысте), вычисленный по его размерам соответственно по двум перпендикулярным направлениям, см;
- D =d+С*L – диаметр бревна на нижнем срезе (комле), вычисленный исходя из диаметра бревна на верхнем срезе (хлысте) и его сбежалости, см;
- L – длина бревна, м;
- С – сбежалость, см/м.
В приведенном выше случае V = 3,14* (232+ 23* 15+152)* 8/12000=0,23 м3 , хотя таблица расчета по кубатурнику дает объем 0,199 м3.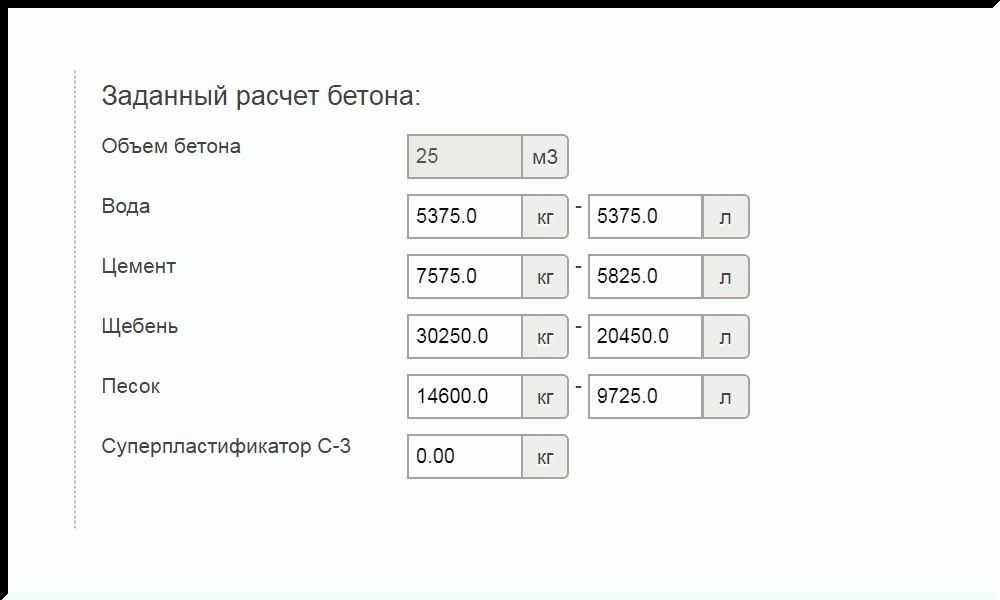 Результат очевиден.
Результат очевиден.
Поэтому, если лес покупать, лучше измерять по ГОСТу, а если продавать, то по приведенной формуле.
Как рассчитать кубатуру бетона: простая формула расчета
Бетон применяется в производстве изделий для строительства, заливке оснований, в ремонтных работах. Чтобы понять, сколько требуется материала для проведения конкретного типа работ, нужно уметь рассчитывать кубатуру. Так как продукт это дорогой, лучше заказывать точное количество, чтобы не было остатков, а значит и дополнительных издержек.
В этой статье мы расскажем, как рассчитать количество бетона для трех основных видов фундамента, монтажа свай, заливки пола, а также перечислим главные инструменты, которые в этом помогут.
Расчет под фундамент
Есть три основных виды оснований под строения: плитные, столбчатые и ленточные. Если вам нужно рассчитать куб бетона для фундамента, ниже приводим инструкции.
Плитный фундамент
Здесь значение высчитывается проще всего. Измерьте основные габариты плит: высоту, ширину и длину. После того как эти параметры получены, достаточно будет перемножить цифры.
Измерьте основные габариты плит: высоту, ширину и длину. После того как эти параметры получены, достаточно будет перемножить цифры.
Единственной проблемой здесь может стать учет ребер жесткости. Их нужно закладывать в объеме в том случае, если нужно дополнительное усиление. Ребра жесткости считаются отдельно, а полученные значения складываются с кубатурой, вычисленной при первоначальном расчете плит.
Столбчатый фундамент
Такой тип основания базируется на сваях. Следовательно, будем отталкиваться от размера одного такого бетонного столба. Формула выглядит так:
S = 3,14 х R2.
В этой формуле R — радиус одной сваи. Это значение умножается на количество используемых столбов на площади под основание. Его можно узнать из проекта.
Ленточный фундамент
Стартовой точкой в расчете станет определение площади, высоты и ширины ленты. Сначала умножаем ширину на высоту, а потом определяем полный объем, умножая площадь сечения на длину ленты.
Так как геометрия может быть разной, отдельно выясняется количество сырья для каждого элемента, а потом эти показатели складываются. Так мы получаем объем, который заказывается при проведении работ.
Расчет кубатуры бетона для заливки пола
Еще одной популярной областью применения бетона является заливка пола в помещениях. Чтобы точно рассчитать количество, нужно использовать формулу:
V = S x H
Где:
- S — площадь поверхности стяжки;
- H — толщина стяжки.
Умножаем одно на другое и получаем количество материала.
Инструменты, необходимые для подсчета
Классический подход: взять измерительный инструмент, ручку с бумагой и посчитать все от руки, но в этом случае возможны ошибки, а каждая неточность стоит денег. Потому лучше использовать специальную программу. Онлайн-калькуляторы можно без труда найти в интернете. Это, пожалуй, самый простой способ правильно посчитать кубатуру бетона.
При возникновении сложностей вам помогут наши специалисты. {n} $
{n} $
удовлетворяющее уравнению $ \phi ( x) = 0 $
называется алгебраической гиперповерхностью степени $m$.
9{( i)} ) = \delta _ {ij} $ (
$ \дельта _ {ij} $
символ Кронекера). Умножая приближенное равенство $ f ( x) \cong {\mathcal P} ( x) $
на $p(x)$
и интегрирование по $\Omega$
приводит к кубатурной формуле типа (1) с $N = \mu $
а также
$$ \тег{2}
C _ {j} знак равно я ( {\ mathcal L} _ {j}), \ \
j = 1 \точки \mu .
$$
Существование интегралов (2) равносильно существованию моментов весовой функции, $ p _ {i} = I ( \phi _ {i} ) $,
$ i = 1 \точки \mu $.
Здесь и далее предполагается, что искомые моменты $ p ( x) $
существует. Кубатурная формула (1), имеющая $ N = \mu $
узлов, не содержащихся ни в одной алгебраической гиперповерхности степени $ m $
и с коэффициентами, определяемыми формулой (2), называется интерполяционной кубатурной формулой. Формула (1) обладает $ m $-свойством, если она является точным равенством, когда $ f ( x) $
является полиномом степени не выше $m$;
интерполяционная кубатурная формула обладает $m$-свойством. Кубатурная формула (1) с $ N \leq \mu $
Кубатурная формула (1) с $ N \leq \mu $
узлов, обладающих свойством $m$, является интерполяционной формулой тогда и только тогда, когда матрица
9{( j)} ) = p _ {i} ,\ \
я = 1 \ точек \ мю .
$$
Естественно требовать, чтобы количество неизвестных совпадало с количеством уравнений: $N ( n + 1) = \mu $.
Это уравнение дает предварительную оценку количества узлов. Если $ N = \mu /( n + 1) $
не является целым числом, полагается $ N = [ \mu /( n + 1)] + 1 $,
где $ [ \mu / ( n + 1)] $
обозначает целую часть $ \mu /( n + 1) $.
Кубатурная формула с таким количеством узлов не всегда должна существовать. Если он существует, то количество его узлов равно $ 1/( n + 1) $
умноженное на количество узлов интерполяционной кубатурной формулы. Однако в этом случае сами узлы и коэффициенты определяются нелинейной системой уравнений (3). В методе неопределенных параметров кубатурную формулу строят, пытаясь придать ей вид, упрощающий систему (3). Это можно сделать, когда $ \Omega $
и $ р ( х) $
иметь симметрии. Положения узлов берутся совместимыми с симметрией $\Omega$
Положения узлов берутся совместимыми с симметрией $\Omega$
и $р(х)$,
и в этом случае симметричным узлам присваиваются одинаковые коэффициенты. Упрощение системы (3) сопряжено с определенным риском: хотя исходная система (3) может быть разрешима, упрощенная система не обязательно.
Пример. Пусть $ \Omega = K _ {2} = \{ — 1 \leq x _ {1} , x _ {2} \leq 1 \} $,
$ р ( х _ {1} , х _ {2} ) = 1 $.
Одного просят построить кубатурную формулу со свойством $7$; $n = 2$,
$ \mu = M ( 2, 7) = 36 $,
и 12 узлов. Узлы расположены следующим образом. Первая группа узлов состоит из точек пересечения окружности радиуса $a$,
с центром в начале координат, с осями координат. Вторая группа состоит из точек пересечения окружности радиуса $b$,
также с центром в начале координат с прямыми линиями $ x _ {1} = \pm x _ {2} $.
Аналогично строится и третья группа, радиус которой обозначается $c$.
Коэффициенты, приписываемые узлам одной группы, одинаковы и обозначаются $A, B, C$
для узлов первой, второй и третьей группы соответственно. {2} $.
{2} $.
Это дает нелинейную систему шести уравнений с шестью неизвестными $ a, b, c $,
$А,В,С$.
Решив эту систему, получим кубатурную формулу с положительными коэффициентами и с узлами, лежащими в $K_{2}$.
9{2} } $.
Теорема 1) Кубатурная формула, инвариантная относительно $ G $
обладает $m$-свойством тогда и только тогда, когда оно точно для всех многочленов степени не выше $m$
которые инвариантны относительно $G$ (см. [5]). Метод неопределенных коэффициентов можно определить как метод построения инвариантных кубатурных формул, обладающих $m$-свойством. В приведенном примере роль группы $G$
может играть группа симметрии квадрата. Теорема 1 имеет существенное значение при построении инвариантных кубатурных формул.
Для простых областей интегрирования, таких как куб, симплекс, шар или сфера, и для веса $ p (x) = 1 $,
можно построить кубатурные формулы, многократно используя квадратурные формулы. Например, когда $ \Omega = K _ {n} = \{ {- 1 \leq x _ {i} \leq 1 } : {i = 1 \dots n } \} $
является кубом, можно использовать квадратурную формулу Гаусса с $ k $
узлы $ t _ {i} $
и коэффициенты $A_{i}$
чтобы получить кубатурную формулу
$$
\int\limits _ {K _ {n} }
f ( x) dx \ cong \
\ сумма _ {я _ {1} \ точки я _ {п} = 1 } ^ {к}
А _ {я _ {1} } \ точки А _ {я _ {п} }
е ( т _ {я _ {1} } \ точки т _ {я _ {п} } )
$$
9\альфа $
такое, что $ 0 \leq \alpha _ {i} \leq 2k — 1 $,
$ i = 1 \ точек n $,
и, в частности, для всех многочленов степени не выше $2k — 1$.
Количество узлов таких кубатурных формул быстро увеличивается, что ограничивает их применимость.
В дальнейшем предполагается, что весовая функция имеет фиксированный знак, скажем
$$ \тег{4}
р ( х) \geq 0 \ \
\mathop{\rm in} \Omega \ \
\textrm{ и } \ \
р _ {1} > 0.
$$
Тот факт, что коэффициенты кубатурной формулы с такой весовой функцией положительны, является ценным свойством формулы.
Теорема 2) Если область интегрирования $ \Omega $
замкнут и $ p ( x) $
удовлетворяет (4), существует интерполяционная кубатурная формула (1), обладающая $ m $-свойством, $ N \leq \mu $,
с положительными коэффициентами и с узлами в $\Omega$.
Вопрос о реальном построении такой формулы пока открыт.
Теорема 3) Если кубатурная формула с весом, удовлетворяющим (4), имеет вещественные узлы и коэффициенты и обладает $m$-свойством, то не менее $\lambda = M(n,l)$
ее коэффициентов положительны, где $ l = [ m/2] $
— целая часть $ m/2 $.
В условиях теоремы 3 число $ \lambda $
является нижней границей количества узлов:
9{(к)} $
и $C_{j}$
реальны.
Что касается кубатурных формул со свойством $ m $, то особенно интересны те, которые имеют минимальное количество узлов. При $ м = 1, 2 $
такие формулы легко найти для любых $n$,
произвольный $\Omega$
и $ p ( x) \geq 0 $;
минимальное количество узлов — это как раз нижняя граница $\lambda$:
В первом случае он равен 1, а в $n+1$
во-вторых. Когда $ m \geq 3 $,
минимальное количество узлов зависит от домена и веса. Например, если $m = 3$,
область центрально-симметрична, и если $p(x)=1$,
количество узлов $2n$;
для симплекса и $p(x)=1$,
это $n+2$.
В силу (4),
$$ \тег{5}
( \ фи , \ фунтов на квадратный дюйм ) = \
I ( \phi \overline \psi \; )
$$
— скалярное произведение в пространстве многочленов. Пусть $ {\ mathcal P} _ {k} $
– векторное пространство многочленов степени $k$
которые ортогональны в смысле (5) всем полиномам степени не выше $k — 1$.
Это пространство имеет размерность $ M (n — 1, k) $—
количество мономов степени $k$.
Многочлены от $ {\ mathcal P} _ {k} $
называются ортогональными многочленами для $ \Omega $
и $p(x)$. {n} ) $,
{n} ) $,
где $m > n/2$,
и в этом случае искомая кубатурная формула считается точной для всех многочленов степени не выше $m — 1$.
Литература
| [1] | Н.М. Крылов, «Приближенное вычисление интегралов», Macmillan (1962) (Перевод с русского) | |
| [2] | ||
| [3] | А.Х. 4] | С.Л. Соболев, Введение в теорию кубатурных формул, Москва (1974) |
| [5] | С.Л. Соболев, «Формулы механической кубатуры на поверхности сферы» Сиб. Мат. ж. , 3 : 5 (1962) с. 769–796 | |
| [6] | И.П. Мысовских, «Интерполяционные кубатурные формулы», М., 1981, |
Комментарии
Многочлен
влияния j-го узла» (т. {(j)}$).
{(j)}$).
«m-свойство» также известно в западной литературе как степень точности; кубатурная формула обладает $m$-свойством, если она имеет степень точности $m$.
Справочник [a1] является одновременно прекрасным введением и углубленным изучением кубатурных формул.
Литература
| [a1] | Энгельс Г., «Численные квадратуры и кубатуры», акад. Press (1980) |
| [a2] | П. Дж. Дэвис, П. Рабинович, «Методы численного интегрирования», акад. Пресса (1984) |
Как процитировать эту запись:
Кубатурная формула. Математическая энциклопедия. URL: http://encyclopediaofmath.org/index.php?title=Cubature_formula&oldid=51796
Эта статья адаптирована из оригинальной статьи И.П. Мысовских (создатель), которая появилась в Математической энциклопедии — ISBN 1402006098. См. Оригинальную статью
Численное интегрирование (квадратура и кубатура)
Определения исчисления >
Численное интегрирование — это способ найти приближенное численное решение определенного интеграла. Вы используете этот метод, когда аналитическое решение невозможно или неосуществимо, или при работе с данными из таблиц (в отличие от функций). Другими словами, вы используете его для вычисления интегралов, которые не могут быть точно проинтегрированы. Цель числовой квадратуры состоит в том, чтобы точно аппроксимировать функцию с минимальным количеством оценок.
Вы используете этот метод, когда аналитическое решение невозможно или неосуществимо, или при работе с данными из таблиц (в отличие от функций). Другими словами, вы используете его для вычисления интегралов, которые не могут быть точно проинтегрированы. Цель числовой квадратуры состоит в том, чтобы точно аппроксимировать функцию с минимальным количеством оценок.
Содержимое:
- Квадратура
- Кубатура
Для функции одной независимой переменной (например, x ) в квадратуре определенный интеграл заменяется суммированием, что позволяет интегрировать многие «хитрые» задачи интегрирования, в том числе со сложными границами в многомерных пространствах. Этот метод также является строительным блоком для численной обработки дифференциальных уравнений.
Как работает числовая квадратура
Обычно в числовой квадратуре для аппроксимации интеграла используются средневзвешенные значения. Общая идея состоит в том, что вы заменяете определенный интеграл
Со взвешенной суммой конечного числа значений подынтегральной функции
В общем случае a = x 0 и b = x n .
Это приводит к приблизительному ответу. Насколько точен ответ, зависит от того, сколько точек выборки выбрано и как взвешены эти вклады.
Числовые квадратурные правила
Правило трапеций.
Следующие числовые квадратурные правила предназначены для одиночных интервалов:
Правило трапеций усредняет левые и правые значения из сумм Римана.
Правило Симпсона — чрезвычайно точный метод аппроксимации (вероятно, самый точный из вариантов сумм Римана). Вместо прямоугольников или трапеций в этом числовом квадратурном методе используется парабола. Вариантом является Правило 3/8 Симпсона , в котором используется немного другая формула.
Правило средней точки использует среднюю точку левого и правого прямоугольников.
Открытые формулы Ньютона-Котеса полезны, когда значения подынтегральной функции даны для равноотстоящих точек. Однако в целом этот метод менее точен, чем другие методы (например, квадратуры Гаусса). Основные шаги:
Основные шаги:
- Разделить функцию на равные части через интервал [a, b],
- Найдите полиномы, которые аппроксимируют функцию (используя метод, называемый интерполяционными полиномами Лагранжа ).
Формулы Ньютона-Котеса могут быть закрытыми (используются все точки) или открытыми (все точки, кроме значений в конечных точках). На следующем изображении показаны замкнутые формулы Ньютона-Котеса. степень точности — наибольшее положительное целое число, которое дает точное значение x k , для каждого значения k:
Простое численное интегрирование с фигурами
Очень простая форма численного интегрирования включает использование квадрата сетка , чтобы найти площадь. Просто наложите квадратную сетку под кривую, затем посчитайте количество квадратов. Если вы используете относительно небольшие квадраты, вы можете получить очень хорошее приближение для многих функций. Если вам нужно только приблизительное приближение и вы не беспокоитесь о получении точного ответа, этот простой метод может подойти.
Если вам нужно только приблизительное приближение и вы не беспокоитесь о получении точного ответа, этот простой метод может подойти.
Существует множество вариаций основного метода. Например, вы можете подсчитывать только полные квадраты или аппроксимировать площади частично заполненных квадратов, возможно, считая каждый частично заполненный квадрат за половину полного квадрата.
Суммы Римана, правила середины, Симпсона и правила трапеций
Суммы Римана (включая правило середины, правило Симпсона и правила трапеций) аналогичны методу «квадратов», описанному выше, за исключением того, что они используют прямоугольники вместо квадратов.
Суммарная сумма Римана использует прямоугольники для аппроксимации площади.
Из этого конкретного набора процедур правило Симпсона является достаточно точным и даже дает точную площадь для любого многочлена третьей степени или меньше. Более подробное объяснение этих методов, включая пошаговые примеры, см. в основной статье о суммах Римана.
в основной статье о суммах Римана.
Квадратура Гаусса
Квадратура Гаусса дает точные решения для многочлена степени не выше 2n – 1. Основная идея заключается в том, что вы используете кривую Гаусса в качестве накладывающейся формы вместо прямоугольников или трапеций.
Сравнение методов гауссовского и трапециевидного численного интегрирования. Правило двух точек дает точный результат, потому что площадь светло-серых областей равна площади темно-серых областей.
Квадратура: ссылки
Абрамовиц, М. и Стегун, И. А. (ред.). «Интеграция». §25.4 в Справочнике по математическим функциям с формулами, графиками и математическими таблицами, 9-е издание. Нью-Йорк: Довер, стр. 885-887, 1972.
Корбит, Д. «Численное интегрирование: от трапеций до RMS: объектно-ориентированное числовое интегрирование». Журнал доктора Добба, № 252, 117–120, 19 октября.96.
Хильдебранд, Ф. Б. Введение в численный анализ. Нью-Йорк: McGraw-Hill, стр. 160-161, 1956.
(2013). Численная квадратура. Получено 22 января 2020 г. с: https://www2.math.ethz.ch/education/bachelor/lectures/fs2013/other/nm_pc/Ch07.pdf
В общем смысле слова « кубатура » процесс нахождения объема твердого тела. В исчислении кубатура определяется как численный метод вычисления нескольких интегралов, в том числе в более высоких измерениях. Например, на трехмерных телах или четырехмерных гиперкубах, где пределы интегрирования — векторы. Это по сравнению с квадратурой, которая представляет собой численное вычисление для одного интеграла [1].
Тройной интеграл для объема куба.
Основная идея аналогична суммам Римана: фигура делится на ряд прямоугольников и находит предел по мере того, как эти прямоугольники становятся тоньше. Для форм в более высоких размерностях (скажем, более 7) используются методы Монте-Карло или аналогичные [2].
Где найти кубатурную формулу
Как вы, наверное, понимаете, количество способов выполнения кубатуры огромно. На самом деле их так много, что им посвящены целые энциклопедии. Большинство академических работ по множественному численному интегрированию относятся к одной из двух книг:
На самом деле их так много, что им посвящены целые энциклопедии. Большинство академических работ по множественному численному интегрированию относятся к одной из двух книг:
- А. Х. Страуд. Приближенное вычисление кратных интегралов, Прентис-Холл, Энглвуд Клиффс, Нью-Джерси (1971). Это издание является достаточно полным. К сожалению, копия обойдется вам примерно в 500 долларов.
- И.П. Мысовских. Интерполяционные кубатурные формулы // Изд-во. Наука, Москва, Ленинград (1981). Тоже всеобъемлющая книга, но проблема в том, что она написана на русском языке.
Веб-сайт Encyclopaedia of Cubature Formulas , разработанный в Бельгии на кафедре компьютерных наук Katholieke Universiteit Leuven, содержит множество кубатурных таблиц. Например, здесь можно найти формулы для куба (включая n-куб) и сферы (включая n-сферу). К сожалению, это старый сайт, и на нем не очень легко ориентироваться или получить к нему доступ (некоторые части сайта предлагают вам войти в систему без дальнейших инструкций).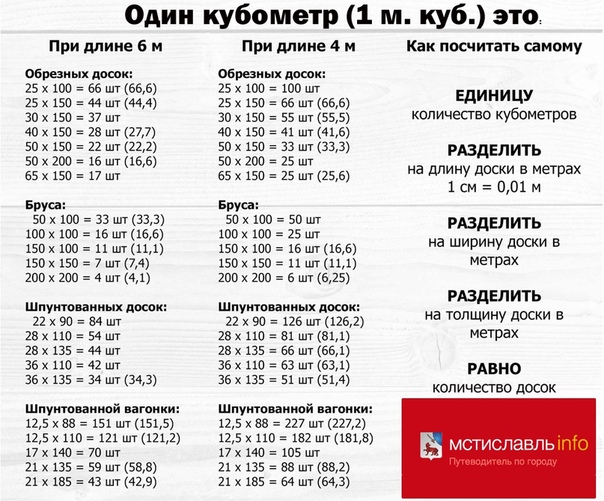
Лучшим решением является использование формул, найденных в некоторых статистических программах. Например, этот пакет R предназначен для адаптивной многомерной интеграции по гиперкубам.
Кубатура: ссылки
[1] Кроммер, А. Р. и Уберхубер, К. В. «Построение кубатурных формул». §6.1 в вычислительной интеграции. Филадельфия, Пенсильвания: SIAM, стр. 155-165, 1998.
[2] Cubature (многомерная интеграция). Получено 8 апреля 2021 г. с: http://ab-initio.mit.edu/wiki/index.php/Cubature_(Multi-diversity_integration)
УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Числовое интегрирование (квадратура и кубатура)» Из StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/numerical-integration/
————————————————— ————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области.
