ПОСТРОЕНИЕ ТРЕТЬЕЙ ПРОЕКЦИИ МОДЕЛИ ПО ДВУМ ЗАДАННЫМ. Как построить профильную проекцию фигуры
Проекции треугольника, многоугольника и круга
TEnd-->nn
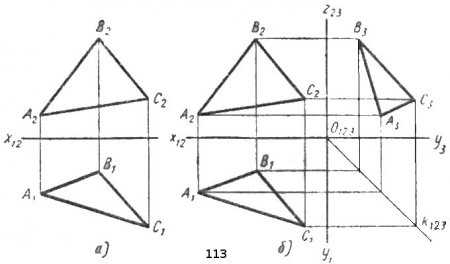
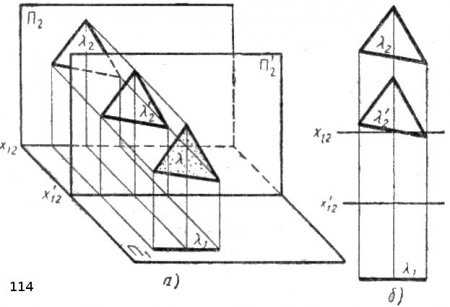
Перенос оси z23y1 вправо или влево перемещает третью проекцию А3В3С3 треугольника вправо или влево, однако не изменяет формы и размеров самой проекции. Перенос оси связан в данном случае с переносом профильной плоскости проекций П3. Подобный перенос возможен и для других плоскостей проекций. Покажем это на примере проецирования треугольника (рис. 114, а), Первоначально мы получили проекции λ2 и λ1 плоскости λ на плоскостях П2 и П1. Если мы переместим фронтальную плоскость проекций в положение П2, то мы получим новую фронтальную проекцию λ2 равную первоначальной проекции λ2; горизонтальная проекция λ1 для обоих положений фронтальной плоскости будет одна и та же. Таким образом, на комплексном чертеже (рис, 114, б) при новом положении оси проекций изменилось только расстояние между горизонтальной и фронтальной проекциями фигуры; форма проекций, их размеры и ориентация относительно осей проекций не изменились. Следовательно, оси проекций можно не изображать на комплексных чертежах; в большинстве случаев без них можно обойтись и тем самым упростить проекционные чертежи. Этой возможностью пользуются на заводах и в проектных организациях, где чертежи выполняются без осей проекций.
n
Для примера изобразим прямоугольник ABCD без осей проекций (рис. 115, а). Расстояние горизонтальной и профильной проекций от фронтальной проекции выберем произвольно. Встает вопрос о том, можно ли теперь «восстановить» положение осей, а следовательно, и плоскостей проекций. Для построения постоянной прямой чертежа (рис. 115, б) используем горизонтальную и профильную проекции любой точки, например точки А. Через точку А1 проведем горизонтальную линию связи, а через точку А3 — вертикальную линию связи. Проведенные прямые пересекутся между собой в точке А0, через которую проведем постоянную прямую k123 под углом 45 градусов к горизонтальной линии связи. Очевидно, что постоянная прямая будет единственной. Этого нельзя сказать о системе координатных плоскостей, которых может быть много. Действительно, одну из систем можно определить, приняв горизонтально-вертикальную линию связи за направление осей проекций x12 и z23. Точка A0 будет для этой системы началом координат O123. Плоскость прямоугольника будет прикасаться своей стороной AD к фронтальной плоскости проекции П2. Вторую систему можно получить, если провести координатные оси х'13 и z'23 через точку О'123, являющуюся точкой пересечения постоянной прямой с линией D2D3. В новой системе прямоугольник будет стоять на горизонтальной плоскости проекций П1, пересекаясь с ней по прямой DC. В промежутке между осями первых двух систем можно провести еще большое количество осей, которые определят новые системы плоскостей. Одну из таких систем определяют оси х212 и z223, пересекающиеся между собой в точке О1, являющейся началом координат третьей системы плоскостей. В последнем случае прямоугольник отстоит от всех трех плоскостей проекций.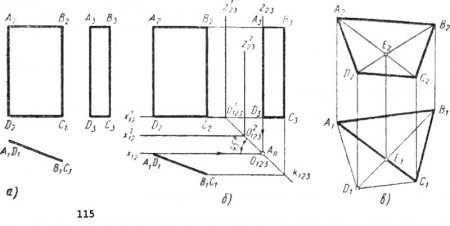
TEnd-->nn
При построении проекций четырехугольника общего положения нельзя взять четыре произвольные точки. Как только мы возьмем три точки, плоскость определится, и четвертую точку надо строить при условии, чтобы она принадлежала этой плоскости. Практически пользуются диагоналями проекций четырехугольника (рис. 115, в).Проекции диагоналей пересекутся между собой в точке Е2. Находим горизонтальную проекцию E2 этой точки на горизонтальной проекции А1С1 будущей диагонали АС; соединяем точки В1 и E1 и на продолжении этой линии находим точку D1 на вертикальной линии связи D2D1. При таком построении четырехугольник ABCD будет плоским. Пользуясь вспомогательными прямыми, пересекающимися со сторонами четырехугольника, можно построить проекции пятиугольника, шестиугольника и т. д.
Построим проекции правильного шестиугольника, вписанного в окружность, при горизонтальном их расположении (рис, 116, а). Построение начинаем с проведения окружности; затем вписываем в нее правильный шестиугольник А1В1C1D1E1F1.
nnTBegin-->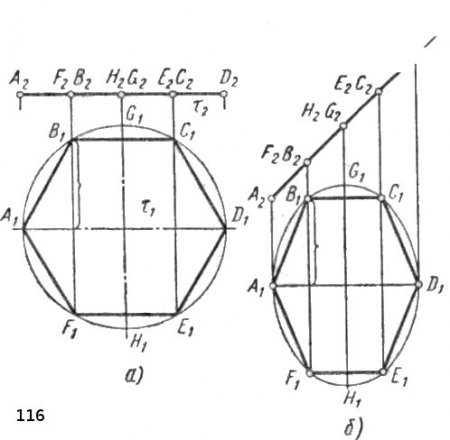
n
Фронтальная проекция шестиугольника изобразится прямой горизонтально расположенной линией A2D2, точки B2F2 и С2Е2, принадлежащие этой линии, попарно совпадут.В практике нередко приходится строить наклонно расположенные многоугольники, и особенно, окружности. Придадим плоскостям шестиугольника и круга наклонное положение, т. е. расположим их во фронтально-проецирующей плоскости т (рис. 116, б). При таком расположении плоскости прямые FB и ЕС шестиугольника и диаметр HG круга останутся фронтально-проецирующими прямыми и спроецируются на плоскость П1 в истинную величину. Наоборот, прямые ВС, AD и FE спроецируются с искажением, зависящим от величины угла наклона плоскости т. В связи с этим горизонтальная проекция шестиугольника не будет являться правильным шестиугольником, а горизонтальная проекция круга будет проецироваться эллипсом, большая ось которого h2G1, малая — A1D1
Аналитический портал Ua-News Главные новости Украины: политика, интернет, шоу-BIZ, спорт, столица.
polynsky.com.kg
Построение - профильная проекция - Большая Энциклопедия Нефти и Газа, статья, страница 3
Построение - профильная проекция
Cтраница 3
На рис. 261 дан пример построения проекций врубки деревянно и стойки. Плоскости Р и Q расположены под утлом к оси цилиндрической стойки и пересекают ее по эллиптическим сегментам, фронтальные проекции которых совпадают с одноименными следами проектирующих плоскостей, а горизонтальные представляют собой круговой сегмент. При построении профильных проекций сегментов расстояние между двумя симметричными точками эллиптических дуг в поперечном направлении ( направление, перпендикулярное к плоскости V) определялось хордой Дг /, длина которой измерялась на горизонтальной проекции. [31]
На рис. 283 дан пример построения проекций врубки деревянной стойки. Плоскости Р и Q расположены под углом к оси цилиндрической стойки и пересекают ее по эллиптическим сегментам, фронтальные проекции которых совпадают с одноименными следами проектирующих плоскостей, а горизонтальные представляют - собой круговой сегмент. При построении профильных проекций сегментов расстояние между двумя Симметричными точками эллиптических дуг в поперечном направлении ( направление, перпендикулярное к плоскости V) определялось хордой Ду, длина которой измерялась на горизонтальной проекции. [32]
Если прямые являются профильными, то для определения взаимного положения прямых необходимо построить профильные проекции этих прямых. Например, рассматривая двухпартийный комплексный чертеж ( на Дг и Я /) прямых АВ и CD ( рисунок 2.6), можно ошибочно сделать заключение, что они параллельны. В действительности прямые скрещиваются, что очевидно после построения профильной проекции. В случае, когда только одна из прямых занимает профильное положение, для определения взаимного положения прямых кроме построения профильной проекции можно использовать метод пропорционального деления отрезка: если прямые пересекаются, то точка пересечения делит обе проекции профильного отрезка в одном и том же соотношении. [34]
Положение отрезка прямой в пространстве определяется двумя его проекциями. Чтобы найти третью проекцию отрезка, необходимо построить третьи проекции ограничивающих его точек. На рис. 73, б стрелками показан ход построения профильной проекции а Ь отрезка АВ по заданным горизонтальной ab и фронтальной а Ъ проекциям. [36]
Опорные точки / и 5 находятся без дополнительных построений. На чертеже положение фронтальной проекции РЗ этой плоскости определяется после построения профильной проекции окружности пересечения. [37]
Нужно построить профильную проекцию. Отложим от нее на линиях проекционной связи отрезки L, S и Ь, равные соответствующим отрезкгм на горизонтальной проекции. Соединив концы этих прямых горизонтальными линиями, а концы отрезков 5Х и S2 также и наклонной прямой, завершим построение профильной проекции угольника. [38]
В пересечении их с профильными проекциями плоскостей среза отмечают профильные проекции характерных точек на линии среза. Пример построения профильной проекции D и по ней фронтальной проекции D отмечен на рис. 9.14. По положению проекций В, С, Б, F строят фронтальные проекции В С Е F точек линии среза. [39]
Если прямые являются профильными, то для определения взаимного положения прямых необходимо построить профильные проекции этих прямых. Например, рассматривая двухпартийный комплексный чертеж ( на Дг и Я /) прямых АВ и CD ( рисунок 2.6), можно ошибочно сделать заключение, что они параллельны. В действительности прямые скрещиваются, что очевидно после построения профильной проекции. В случае, когда только одна из прямых занимает профильное положение, для определения взаимного положения прямых кроме построения профильной проекции можно использовать метод пропорционального деления отрезка: если прямые пересекаются, то точка пересечения делит обе проекции профильного отрезка в одном и том же соотношении. [41]
В некоторых случаях бывает затруднительным определение опорных точек, необходимых для правильного построения линии пересечения. Так, на рис. 6.10 - пересечение конуса и сферы - линия пересечения построена вначале без определения точек Е и F ( неявные опорные точки) на пересечении профильного меридиана т сферы с конусом. Искать эти точки с помощью вспомогательной плоскости, проходящей через эту окружность, нецелесообразно, потому что плоскость пересечется с конусом по гиперболе. Но когда построены фронтальная и горизонтальная проекции кривой, легко отметить на них проекции указанных точек и найти их профильные проекции ЕЗ и F3, необходимые для построения профильной проекции линии пересечения, на проекции меридиана т - окружности. [42]
Однако в некоторых случаях такие построения необходимы. Так как эта плоскость может быть или плоскостью общего положения, или профильно проецирующей, то строим какую-либо ее линию уровня, например горизонталь А. Если горизонталь h не вырождается в профильно проецирующую прямую ( см. рис. 2.9), то плоскость 6 занимает общее положение. Если же горизонталь Л будет к тому же профильно проецирующей ( см. рис. 2.10), то и плоскость 0 будет профильно проецирующей. Конечно, положение плоскости 6 можно было определить и построением профильной проекции AjB Cj задающего ее треугольника ЛВС. [44]
Страницы: 1 2 3
Построение - фронтальная проекция - Большая Энциклопедия Нефти и Газа, статья, страница 1
Построение - фронтальная проекция
Cтраница 1
Построение фронтальной проекции этой части понятно из чертежа. [1]
Построение фронтальной проекции сечения можно выполнить независимо от уже построенной проекции сечения на плоскость Я. Для этой цели следует перейти от системы У / Я к У / ЯГ Новая плоскость Н1 перпендикулярна к фронтали АВ заданной плоскости. [2]
Построение фронтальной проекции диффузора производится в следующей последовательности ( рис. 58): из центра о радиусом Rcp описывается дуга M. [3]
Построение фронтальных проекций окружностей может осуществляться с помощью горизонтальных и фронтальных секущих плоскостей. Можно и не пользоваться вспомогательными плоскостями, так как горизонтальные проекции всех точек кривых известны и фронтальные их проекции могут быть определены с помощью параллелей сферы. [4]
Построение фронтальной проекции линии пересечения цилиндрической поверхности конусом ( рис. 427) выполнено по исходным точкам, взятым на профильной проекции цилиндра. [5]
Для построения фронтальных проекций ( 2у, Зу, 4V) точек, принадлежащих линии пересечения, проводят вспомогательные фронтальные плоскости, линии сечения которых обозначены А-А, Б - Б, В-В, пересекающие шаровую поверхность по окружностям радиусов Ид, Rs и Rq, а цилиндрическую - по образующим. [6]
Для построения фронтальных проекций образующих 4 и 8 использован размер у1 ( глубина), параллельный одноименной оси координат. [8]
Для построения фронтальной проекции треугольника проводим в любом месте чертежа фронтальную проекцию т п оси вращения параллельно оси проекций. [9]
Для построения фронтальных проекций гипербол пользуются вспомогательными горизонтальными плоскостями. [10]
Для построения фронтальной проекции сечения необходимо спроецировать точки 1, 2, 3 и 4, принадлежащие секущей плоскости, на фронтальную проекцию. Проводим через точки 2 3 vi 4 горизонтальные проекции фронтален, а затем строим фронтальные их проекции. В пересечении с соответствующими фронтальными проекциями ребер получим искомые проекции точек пересечения ребер с плоскостью. Соединив полученные точки прямыми в последовательности, которая задана горизонтальной проекцией, и определив невидимые участки сечения, закончим построение. [11]
Для построения фронтальной проекции сетки горизонтальную проекцию боковой поверхности тела делят на части, - 1ft ело и размер которых соответствует вертикальным делениям сетки на развертке. [12]
Однако построение указанных фронтальных проекций часто не является необходимым и их не показывают на чертеже. [13]
Для построения фронтальной проекции линии пересечения необходимо отметить заданные проекции точек пересечения ребер каждой из призм с гранями другой призмы. По горизонтальной и профильной проекциям видно, что четыре ребра шестиугольной призмы пересекаются с двумя гранями треугольной призмы, а два боковых ребра треугольной призмы пересекаются с двумя гранями шестиугольной призмы. Фронтальные проекции отрезков 3 - 5 и 5 - 6 линии пересечения невидимы, так как они расположены на задних гранях шестиугольной призмы. [14]
Для построения фронтальной проекции фигуры сечения достаточно отметить на П2 точки Az и В2; отрезок А2В2 и будет этой проекцией. Далее можно построить сколько угодно точек горизонтальной проекции. Для этого нужно отметить какую-либо точку фигуры сечения ( на фронтальной проекции) и провести через нее простую вспомогательную линию на поверхности конуса ( образующую конуса или окружность на его поверхности), изобразив ее фронтальную проекцию. [15]
Страницы: 1 2 3 4
www.ngpedia.ru
Построение - профильная проекция - Большая Энциклопедия Нефти и Газа, статья, страница 1
Построение - профильная проекция
Cтраница 1
Построение профильной проекции по данной фронтальной и горизонтальной проекциям может быть выполнен несколькими способами. На рис. 82 показано построение профильной проекции точки с помощью вспомогательной линии, проведенной под углом 45 через начало координат. [1]
Построение профильной проекции по данной фронтальной и горизонтальной проекциям может быть выполнено несколькими способами. На рис. 96, б показано построение профильной проекции точки с помощью вспомогательной линии, проведенной под углом 45 к оси у, через начало координат. [2]
Для построения профильной проекции шара намечают точку Оу. [3]
Для построения профильной проекции пирамиды намечают базовую плоскость, проходящую через какую-либо точку пирамиды, например, фронтальную плоскость ( следы тн и п р), проведенную через точку В. Профильную проекцию AW точки А получим, если отложим от BW на горизонтальной линии расстояние /, равное расстоянию АН от тн. Аналогично находят Cw Проекцию Bw отмечают в зависимости от выбираемой базовой плоскости. [4]
Для построения профильной проекции конуса выбирают за базу ось симметрии конуса, которую проводят в удобном месте. Профильные проекции AW и Bw находят, отложив на профильной проекции от нижнего основания по оси конуса высоту h точки А и высоту / точки В. [5]
Для построения профильных проекций Mw и NW точек контурных образующих откладывают от CV вправо и. [6]
Для построения профильной проекции шара на уровне Ov намечают точку Ow и проводят через нее вертикальную ось. [7]
Для построения профильной проекции пирамиды намечают базовую плоскость, проходящую через какую-либо точку пирамиды, например фронтальную плоскость ( следы тн и nw), проведенную через точку В. [8]
Для построения профильной проекции конуса выбирают за базу ось симметрии конуса, которую проводят в удобном для проектирования месте. [9]
Для построения профильной проекции усеченного конуса проводят прямую, на которой откладывают 0 ySw - высоту конуса. Влево от Oiff на расстоянии R отмечают точку, соединив которую с Sw получают профильную проекцию контурной образующей. V и Fw промежуточных точек находят аналогично или обычным проектированием. [10]
Для построения профильной проекции усеченного конуса проводят в этой проекции ось симметрии конуса, которая служит базой для построения. [11]
Для построения профильной проекции усеченного конуса проводят вертикальную прямую, на которой откладывают высоту конуса OwSw-Влево от GW на расстоянии R отмечают точку, соединив которую с Sw, получают профильную проекцию контурной образующей. [12]
Для построения профильной проекции усеченного конуса проводят в этой проекции ось симметрии конуса, которая служит базой для построения. На выбранной оси от основания конуса откладывают высоту точки А и отмечают А у. Профильные проекции Kw и w промежуточных точек находят, отложив на высоте этих точек вправо и влево от оси симметрии соответствующие расстояния ЯБ ОнКн ОиЬн. Профильные проекции D y и Е у находят аналогично построению Сц. Вуг - Полученные проекции точек соединяют плавной кривой. [13]
При построении профильной проекции можно использовать прямую преломления, которая проводится под углом 45 к горизонтальным или вертикальным линиям связи ( черт. Нетрудно видеть, что эта прямая обеспечивает сохранение глубин данных точек. [14]
Рассуждения при построении профильной проекции предмета аналогичны приведенным в предыдущем примере. [15]
Страницы: 1 2 3
www.ngpedia.ru
ПОСТРОЕНИЕ ТРЕТЬЕЙ ПРОЕКЦИИ МОДЕЛИ ПО ДВУМ ЗАДАННЫМ — КиберПедия
Порядок построения.
1)Провести координатные оси в центре листа и главную ось под 45˚
2)Построить две заданные проекции по размерам, применяя соответствующий масштаб увеличения, чтобы коэффициент заполнения чертежа был не менее 75%.
3)Провести линии связи на профильную плоскость от двух данных изображений и обозначить характерные точки.
4)Прочертить контур детали в тонких линиях.
5)Обвести видимый контур сплошной основной, а невидимый- штриховой линией.
6)Нанести размерные линии и проставить размеры. Должны быть проставлены все размеры, заданные в задании, но распределить их по видам надо равномерно, стараясь проставлять размеры различных элементов там, где это более наглядно и контур элемента видимый.
ЭСКИЗ И ТЕХНИЧЕСКИЙ РИСУНОК МОДЕЛИ.
Эскиз- это чертеж в трех проекциях, выполненный от руки без масштаба, но с сохранением пропорций детали.
Технический рисунок- это наглядное изображение, аксонометрия, выполненная от руки.
Выполнение рисунка детали начинают с построения его габаритного очертания-«клетки», выполняемой «от руки» тонкими линиями (в данном случае - параллелепипед). Затем деталь мысленно расчленяют на отдельные геометрические элементы, постепенно зарисовывая все элементы (части) детали.
Рис. 22
Технические рисунки предмета получаются более наглядными, если их покрыть штрихами (рис.22, б). При нанесении штрихов считают, что лучи света падают на предмет справа и сверху или слева и сверху.
Освещенные поверхности штрихуют тонкими линиями на большом расстоянии друг от друга, а теневые —более толстыми линиями, располагая их чаще. Боковые поверхности пирамиды и конуса штрихуют линиями, проходящими через их вершину.(рис.72а-д)
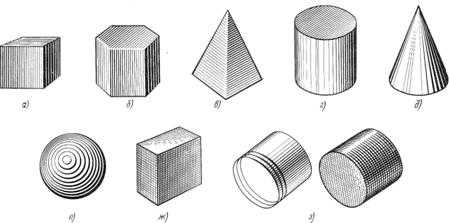
Рис. 23
На изображения сферических поверхностей и поверхностей вращения наносят криволинейные штрихи (части концентрических окружностей) разной толщины и с разными промежутками между штрихами.
Иногда изображения геометрических тел или деталей покрывают шраффировкой, которая представляет собой сложную штриховку, например, в виде сетки. Освещенные поверхности предмета покрывают тонкими линиями шраффировки. По мере приближения к затемненным местам эти линии утолщают. Кроме того, ближние к наблюдателю контурные линии предмета выполняют более толстыми, чем удаленные.
На рисунках деталей (см. рис.23 е-з)) применена подобная
штриховка.
Зарисовывая деталь с натуры (например кронштейн, рис.24), надо не только внимательно рассмотреть форму, но и сравнить соответствие размеров отдельных элементов детали.. На рис.24 дан рисунок этой детали с учетом пропорций ее частей.
С помощью разрезов на рисунках и аксонометрических проекциях можно показать внутреннюю форму детали.
Приемы выполнения разрезов
Полые модели и детали выполняют в аксонометрии с разрезами. Это показано на рис. 25, где изображена деталь с отверстиями, в разрезе.
Если окружность неполная, то для ее изображения вычерчивают тонкой линией полный овал или эллипс, а затем обводят контурной линией нужную часть овала (рис. 25).
Список литературы
1. Р.С.Миронова, Б.Г.Миронов.Инженерная графика. М.:, Высшая школа.; Издательский центр «Академия», 2001. -288 с.
2. А.М.Бродский, Э.М.Фазлулин, В.А. Халдинов. Инженерная графика. М.: ИРПО: .; Издательский центр «Академия», 2003 – 400 с.
3. А.А. Чекмарев, В.К. Осипов. Справочник по черчению. М.: .; Издательский центр «Академия», 2005 – 336 с
4.В.П.Куликов. «Стандарты инженерной графики». М.:, «Форум»,2008- 240с
Варианты заданий
Графическая работа 1. Выполнить на формате А3 чертежи деталей с сопряжениями, уклоном и конусностью.
Графическая работа 2
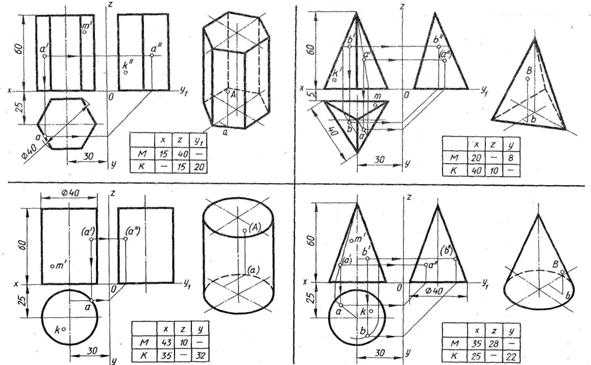Перечертить геометрические тела и построить принадлежащие их поверхностям точки A,B,M,K на ортогональном чертеже и изометрии.
Графическая работа 3
| Обозначение | № варианта | |||||||||
| d | 60 | 58 | 54 | 62 | 60 | 58 | 54 | 62 | 60 | 58 |
| h | 70 | 65 | 72 | 68 | 70 | 65 | 72 | 68 | 70 | 65 |
| m | 32 | 42 | 40 | 33 | 32 | 42 | 40 | 33 | 32 | 42 |
| α˚ | 60 | 45 | 45 | 60 | 60 | 45 | 45 | 60 | 60 | 45 |
|
Пример выполнения
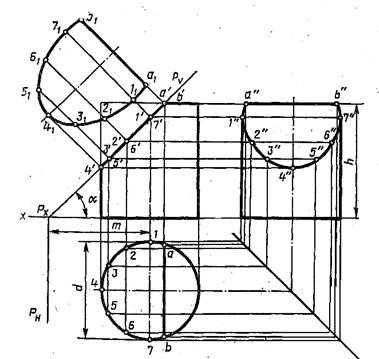
Графическая работа 4
|
| Обозна чение | № варианта | |||||||||
| d | 50 | 55 | 60 | 50 | 56 | 60 | 52 | 55 | 60 | 54 |
| h | 55 | 60 | 65 | 56 | 62 | 65 | 55 | 60 | 70 | 56 |
| а | 37 | 60 | 46 | 38 | 66 | 42 | 36 | 66 | 35 | 38 |
| α˚ | 45 | 30 | 45 | 45 | 30 | 45 | 45 | 30 | 45 | 45 |
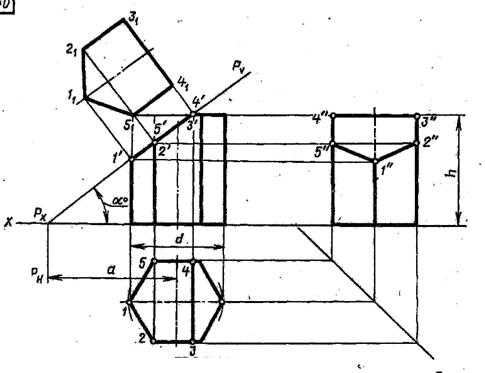
Графическая работа 5
|
| Обозна чение | № варианта | |||||||||
| R | 45 | 40 | 42 | 45 | 42 | 40 | 45 | 44 | 40 | 45 |
| D | 80 | 90 | 88 | 85 | 95 | 45 | 80 | 94 | 45 | 85 |
| h | 90 | 90 | 90 | 90 | 90 | 90 | 90 | 90 | 90 | 90 |
| k | 110 | 110 | 110 | 100 | 110 | 110 | 110 | 110 | 110 | 100 |
Пример выполнения
Возможные варианты
Графическая работа 6
|
Возможные варианты
| Обозна чение | № варианта | |||||||||
| d | 55 | 54 | 70 | 56 | 55 | 54 | 70 | 56 | 54 | 56 |
| h | 65 | 72 | 70 | 68 | 64 | 72 | 68 | 68 | 65 | 71 |
| m | 10 | 8 | 15 | 16 | 10 | 8 | 14 | 16 | 9 | 8 |
| е | 55 | 72 | 75 | 60 | 56 | 72 | 76 | 60 | 55 | 71 |
| h2 | 38 | 45 | 48 | 40 | 38 | 45 | 47 | 40 | 38 | 45 |
| а | 44 | 45 | 52 | 40 | 44 | 45 | 50 | 40 | 44 | 45 |
| k | 74 | 84 | 108 | 70 | 74 | 84 | 110 | 70 | 74 | 84 |
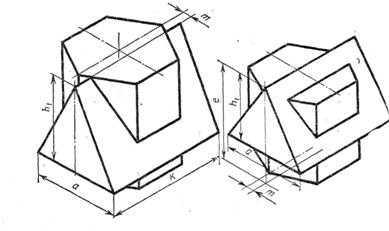
Графическая работа 7
Построить третью проекцию детали по двум заданным и ее технический рисунок с вырезом четверти
cyberpedia.su
Аксонометрические проекции. Плоские фигуры в аксонометрии
⇐ ПредыдущаяСтр 4 из 5Следующая ⇒
Аксонометрические проекции представляют собой наглядное и достаточно точное изображение предметов. К аксонометрическим проекциям относится косоугольная фронтальнодиметрическая проекция и прямоугольная изометрическая проекция.
Слово ”аксонометрия” - греческое, в переводе означает измерение по осям, или измерение параллельно осям.
Аксонометрические проекции широко применяют в качестве иллюстраций в учебных пособиях, различных инструкциях, на плакатах.
Во фронтальнодиметрической (диметрии) ось ОХ располагают горизонтально, ось ОZ под углом 90° к оси ОХ, а ось ОY под углом 45° к горизонтальной линии. В изометрической проекции (изометрии) ось ОZ расположена вертикально, а оси ОХ и ОY составляют с ней углы, равные 120о. На рис. 64 показаны положение осей, приемы построения осей, построение осей при выполнении технических рисунков.
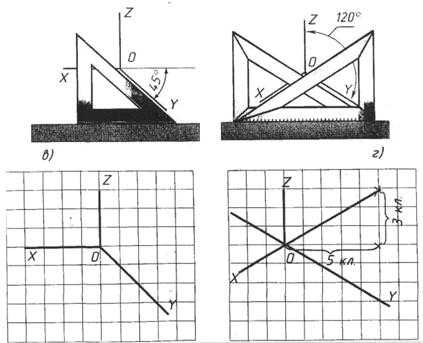
Рис. 64. Положение осей при построении аксонометрических проекций
“Диметрия” в переводе с греческого означает “двойное измерение”. В диметрии по осям ОХ и ОZ откладывают действительные размеры, а по оси ОY- в два раза меньше.
“Изометрия” в переводе с греческого означает “равные измерения”. В изометрии по осям ОХ, ОY, ОZ и линиям им параллельным откладывают действительные размеры.
Построение аксонометрических проекций начинают с изображения основания, т.е. плоских фигур, расположенных в одной из плоскостей. Рассмотрим сначала изображение плоских фигур в аксонометрии, так как знание приемов построения плоских фигур необходимо для построения аксонометрических проекций геометрических тел.
Пример 1. Построение аксонометрических проекций равностороннего треугольника.
Треугольник расположен на фронтальной плоскости (рис. 65).
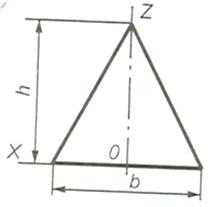
Рис. 65. Треугольник на фронтальной плоскости
По оси ОХ откладывают размер b по оси ОZ - высоту h, точки соединяют (для изометрии и диметрии).
Треугольник расположен на горизонтальной плоскости (рис. 66).
Рис. 66. Треугольник на горизонтальной плоскости
По оси ОХ откладывают размер b, а по оси ОY- высоту h треугольника(в изометрии), в димертии по оси ОY- половину высоты треугольника.
Треугольник расположен на профильной плоскости (рис. 67).
Рис. 67. Треугольник на профильной плоскости
По оси ОY откладывают размер b в изометрии, в диметрии по оси ОY - половину размера b треугольника. По оси ОZ откладывают h высоту треугольника.
Пример 2. Построение аксонометрических проекций правильного шестиугольника. Шести-угольник вписывают в окружность, разделив окружность на шесть равных частей радиусом окружности.
Шестиугольник лежит на фронтальной плоскости (рис. 68).
Рис. 68. Шестиугольник на фронтальной плоскости
По оси ОХ откладывают радиусы описанной окружности, равные стороне шестиугольника из точки О влево и вправо. По оси ОZ из точки О откладывают отрезки, равные половине расстояния между противоположными сторонами шестиугольника вверх и вниз, размер S.Через полученные точки на оси ОZ проводят линии, параллельные оси ОХ, и из точки пересечения откладывают на них отрезки, равные половине стороны шестиугольника. Полученные шесть точек соединяют.
Шестиугольник расположен на горизонтальной плоскости (рис. 69).
Рис. 69. Шестиугольник на горизонтальной плоскости
Построение выполняют так, как было рассмотрено, с той лишь разницей, что размер S между противоположными сторонами для диметрии берут в два раза меньше.
Шестиугольник расположен на профильной плоскости (рис. 70).
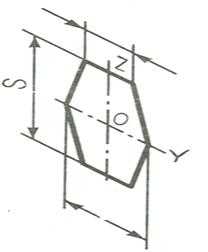
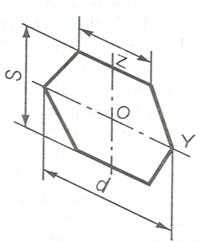
Рис. 70. Шестиугольник на профильной плоскости
В этом случае размер, равный диаметру и размер, равный стороне шестиугольника берут в два раза меньше для диметрии.
Окружность в изометрии
Окружность в изометрии представляет собой замкнутую кривую линию, которая называется эллипсом. Эллипсы строить сложно, поэтому в практике черчения вместо них строят овалы.
Овал - замкнутая циркульная кривая, очерченная дугами окружностей. Овал удобно строить, вписывая в ромб, который является изометрической проекцией квадрата.
Рассмотрим пример построения окружности в изометрии, лежащей на горизонтальной плоскости(рис. 71).
Рис. 71. Построение окружности в изометрии
Чтобы построить овал надо найти точки, принадлежащие овалу и точки, из которых проводят дуги окружности. Откладываем по осям ОХ и ОY размер, равный диаметру заданной окружности, строим ромб. Делим стороны ромба пополам и через полученные точки проводим линии, параллельные осям ОХ и ОY, точки 1,2,3,4 будут принадлежать овалу. Находим точки, из которых будем проводить дуги окружности, две точки (а, в) уже есть, еще две точки (с, d) лежат на большей диагонали ромба. Проводим большую диагональ, соединяем точку 1 и точку 2 с точкой в. Точки пересечения проведенных линий с большей диагональю есть точки с и d.
Строим овал, для этого из точек а и в радиусом, равным а3 проводим дуги, затем из точек с и d, радиусом с1 еще две дуги, получаем овал.
Овалы, расположенные на фронтальной и профильной плоскостях, строят также (рис. 72).
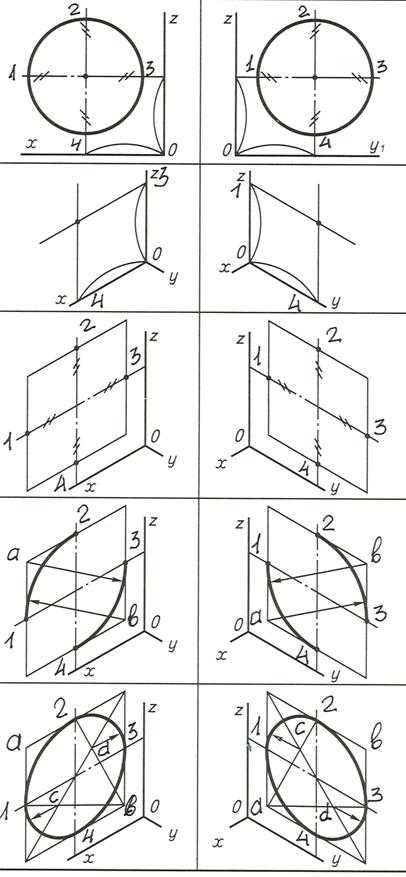
Рис. 72. Построение овалов, расположенных на фронтальной и профильной плоскостях
Из рассмотренных аксонометрических проекций большим преимуществом пользуется изометрия, поэтому в дальнейшем будем проводить построение геометрических тел и деталей только в изометрии.
Вы уже знаете, что форма любого предмета это сочетание геометрических тел или их частей. В основании каждого геометрического тела лежит определенная фигура. Построив фигуру основания в нужной плоскости, можно легко достроить ее до геометрического тела.
Пример 1. Построение параллелепипеда в изометрии.
1. Строим чертеж параллелепипеда в трех видах.
2. Построение параллелепипеда в изометрии начинаем с нижнего основания, откладываем по оси ОХ- длину, а по оси ОY- ширину, достраиваем изометрическую проекцию прямоугольника, затем из вершин прямоугольника проводим линии параллельно оси ОZ, откладываем высоту, соединяем точки и определяем видимость граней (рис. 73).
Рис. 73. Чертеж параллелепипеда в трех видах и изометрии
Пример 2. Построение шестиугольной призмы в изометрии.
1. Строим чертеж призмы в трех видах.
2. Построение начинаем с нижнего основания. Строим шестиугольник в изометрии на плоскости Н, затем из вершин шестиугольника проводим линии параллельно оси О Z и на них откладываем высоту, соединяем точки и определяем видимость граней (рис. 74).
Рис. 74. Чертеж призмы в трех видах и изометрии
Пример 3. Построение четырехугольной пирамиды в изометрии.
1. Строим чертеж пирамиды в трех видах.
2. Построение начинаем с нижнего основания, затем из центра основания проводим линию параллельно оси ОZ, откладываем высоту пирамиды, соединяем полученные точки и определяем видимость граней (рис. 75).
Рис. 75. Чертеж пирамиды в трех видах и изометрия
Пример 4. Построение цилиндра в изометрии.
1. Строим чертеж цилиндра в трех видах. Построение начинаем с нижнего основания.
2. Строим овал и из центра овала проводим линию параллельно оси ОZ, через полученную точку проводим линии, параллельно осям ОХ и ОY.
3. Строим овал (верхнее основание), соединяем верхнее основание касательными линиями с нижним основанием (рис. 76).
Рис. 76. Чертеж цилиндра в трех видах и изометрия
Пример 5. Построение детали в изометрии по чертежу (рис. 77).
Рис. 77. Чертеж детали в двух видах и изометрия
1. Анализируем геометрическую форму детали по чертежу, определяем симметричность.
2. Построение начинаем с нижнего основания, строим параллелепипед.
3. Находим центр верхнего основания параллелепипеда, через центр проводим линии параллельно осям ОХ и ОY.
4. Строим меньший параллелепипед, определяем видимость граней.
5. Проверяем и обводим.
Построение аксонометрической проекции детали от ее нижнего основания является универсальным и используется для построения деталей любой степени сложности.
Читайте также:
lektsia.com
Проецирование плоских фигур - Технические чертежи
Проецирование плоских фигурКатегория:
Технические чертежи
Проецирование плоских фигурЗная правила построения проекций точек и отрезков прямых, можно вычертить проекции любой плоской фигуры: прямоугольника, треугольника, круга, так как каждая фигура ограничена отрезками прямых или кривых линий. Проекции фигур обычно строят по проекциям вершин, которые потом соединяют между собой. Так, для построения плоской фигуры, например треугольника, нужно из его вершин А, В и С провести проецирующие прямые на горизонтальную, фронтальную и профильную плоскости проекций. Построение проекций каждой вершины треугольника сводится к построению проекции точки. Проецирующие прямые пересекут горизонтальную, фронтальную и профильную плоскости проекций соответственно в точках а, в и с; а’, в’и с’; а”, в” и с”, которые будут являться проекциями вершин А, В и С.
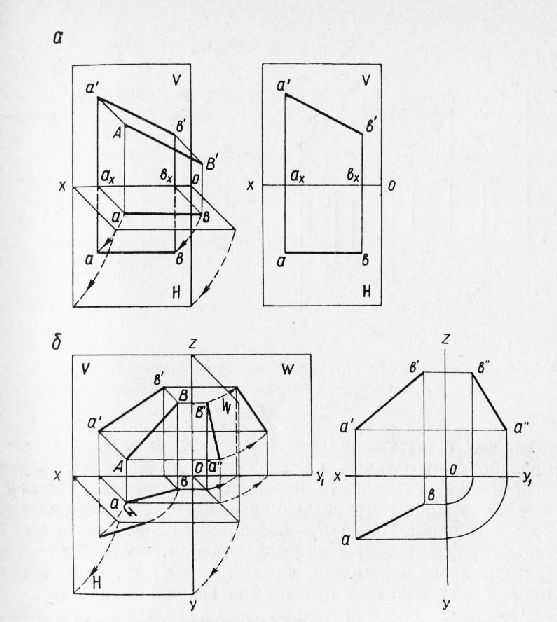
Рис. 1. Проецирование отрезка прямой линии: о — на две плоскости проекций; б — на три плоскости проекций.
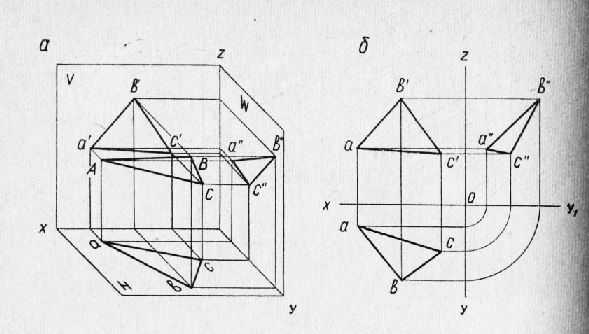
Рис. 2. Проецирование треугольника: а — наглядное изображение; б — эпюр.
Соединив последовательно прямоугольные проекции вершин треугольника прямыми линиями, получим очертания горизонтальной, фронтальной и профильной проекций изображаемого треугольника.
Для получения чертежа плоской фигуры следует совместить плоскости проекций. Тогда на эпюре тот же треугольник изобразится проекциями своих сторон: горизонтальными ав, вс и ас, фронтальными а’в’, в’с’ и а’с’ и профильными а” в”, в” с” и а” с”.
Читать далее:
Проекции геометрических тел
Статьи по теме:
pereosnastka.ru
