Содержание
Расчет сопротивления проводника – формула
4.6
Средняя оценка: 4.6
Всего получено оценок: 97.
4.6
Средняя оценка: 4.6
Всего получено оценок: 97.
Сопротивление проводника ограничивает величину тока в электрической цепи. Чем больше величина сопротивление, тем меньше ток. Расчет сопротивления проводника можно произвести двумя способами: первый способ заключается в использовании формулы закона Ома, а второй вариант расчета подразумевает знание геометрических размеров проводника и удельного сопротивления вещества, из которого он сделан.
Почему проводник “сопротивляется”?
Напряжение U, поданное на концы проводника, создает внутри него электрическое поле, которое приводит в движение свободные электроны вещества. Электроны, получив дополнительную кинетическую энергию, начинают двигаться упорядоченно в одном направлении, создавая тем самым электрический ток цепи.
В процессе движения электроны сталкиваются с нейтральными и заряженными атомами, из которых стоит проводник, теряют энергию. Масса атома превосходит массу электрона в тысячи раз, поэтому их столкновение приводит к изменению направления движения электронов и потере скорости (“торможению”).
Масса атома превосходит массу электрона в тысячи раз, поэтому их столкновение приводит к изменению направления движения электронов и потере скорости (“торможению”).
Таким образом возникает сопротивление протеканию (нарастанию) тока.
Рис. 1. Электрический ток в проводнике ограничивается столкновением электронов с атомами.
Расчет сопротивления с помощью закона Ома
Немецкий физик Георг Ом в 1826 г. обнаружил, что отношение напряжения U между концами металлического проводника, являющегося участком электрической цепи, к силе тока I есть величина постоянная:
$ R={U \over I}=const $ (1),
где:
U — напряжение, В;
I — сила тока, А;
R — сопротивление, Ом.
Эту величину стали называть электрическим сопротивлением. Пользуясь этой формулой, можно экспериментально определить величину неизвестного сопротивления.
Рис. 2. Схема измерения напряжения и тока для определения сопротивления участка цепи.
Для этого амперметром измеряется величина электрического тока через сопротивление, а вольтметром — напряжение на участке цепи. Далее, применяя формулу (1), вычисляется значение R.
Единица измерения названа в честь Георга Ома. Электрическим сопротивлением 1 Ом обладает участок цепи, на котором при силе тока 1 А напряжение равно 1 В:
$$ 1 Ом = { 1 В\over 1 A} $$
Расчет с помощью удельного сопротивления
Расчет сопротивления проводника можно произвести без измерения величин напряжения и тока. Но для этого необходимо знать дополнительную информацию о проводнике.
Рис. 3. Проводник с поперечным сечением S и длиной L, через который течет ток I.
Георг Ом и другие исследователи опытным путем определили, что сопротивление проводника прямо пропорционально длине проводника L и обратно пропорционально площади поперечного сечения проводника S. Эту закономерность можно описать формулой расчета сопротивления проводника:
$ R = ρ *{ L\over S} $ (2)
Коэффициент ρ был назван удельным сопротивлением.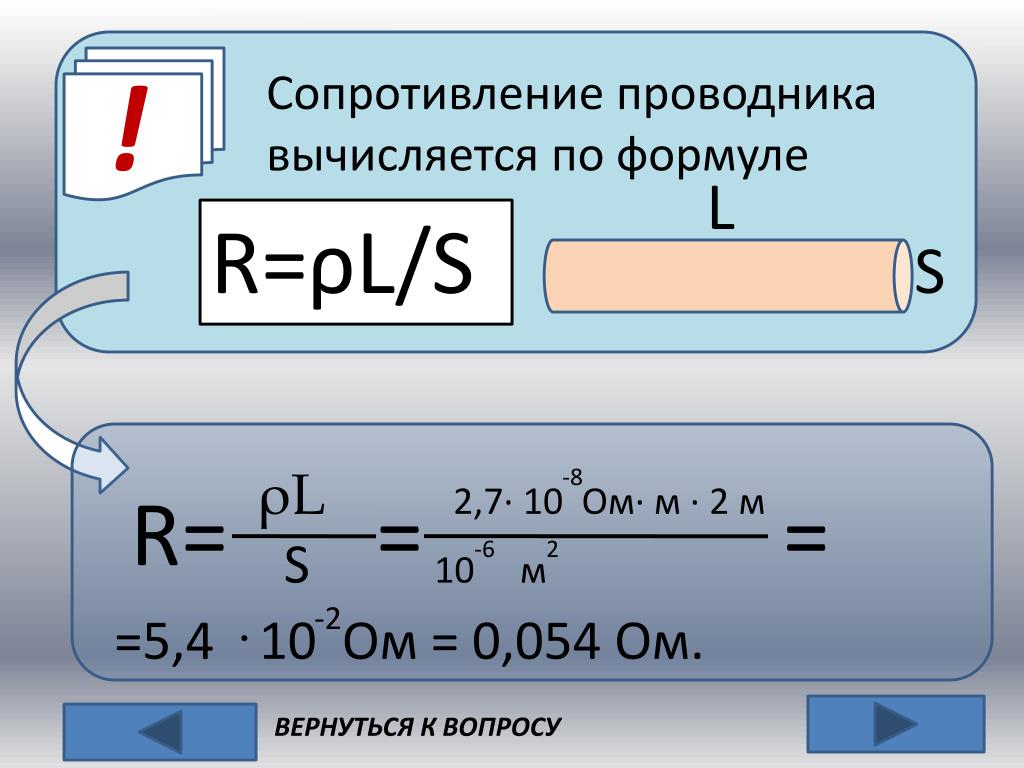 2\over м} $. Этим объясняется использование такого довольно дорогого металла для пайки особенно важных радиодеталей (микросхем, микропроцессоров, электронных плат), которые должны как можно меньше нагреваться в процессе работы.
2\over м} $. Этим объясняется использование такого довольно дорогого металла для пайки особенно важных радиодеталей (микросхем, микропроцессоров, электронных плат), которые должны как можно меньше нагреваться в процессе работы.
Что мы узнали?
Итак, мы узнали, что расчет сопротивления проводника можно произвести двумя способами. Первый расчет проводится с помощью формулы закона Ома после измерения величин напряжения и тока. Для второго расчета необходима информация о геометрических размерах проводника и его удельном сопротивлении.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.6
Средняя оценка: 4.6
Всего получено оценок: 97.
А какая ваша оценка?
Формула сопротивления в физике
Содержание:
- Определение и формула сопротивления
- Вычисление сопротивления при соединении проводников
- Единицы измерения сопротивления
- Примеры решения задач
Определение и формула сопротивления
Определение
Скалярную физическую величину, (обычно обозначаемую R) равную:
$$R=\int_{1}^{2} \rho \frac{d l}{S}(1)$$
называют сопротивлением участка цепи между сечениями 1 и 2. В выражении (1) имеем
В выражении (1) имеем
$\rho$ – удельное сопротивление проводника,
S – площадь поперечного сечения проводника, dl — элемент длины проводника.
Если проводник является однородным ($\rho$=const) и имеет форму цилиндра (S=const), то формула (1) может быть представлена как:
$$R=\rho \frac{l}{S}(2)$$
где l – длина участка рассматриваемого проводника.
Надо отметить, что удельное сопротивление проводника ($\rho$) –
это сопротивление проводника единичной длины с поперечным сечением равным единице. Или иначе говорят, что удельное сопротивление
вещества – это сопротивление куба с ребром 1 м изготовленного из рассматриваемого вещества, которое выражено в Ом, при токе,
который параллелен ребру куба. Величина обратная удельному сопротивлению:
$$\sigma=\frac{1}{\rho}(3)$$
называется удельной проводимостью. Измеряется удельное сопротивление в системе СИ
в [$\rho$]=Ом•м. Эта характеристика проводника зависит от температуры,
в простейшем случае эта зависимость может быть линейна:
$$\rho=\rho_{0}(1+\alpha t)(4)$$
где $\rho_{0}$ – удельное сопротивление проводника при
температуре равной 0C, t — температура в градусах Цельсия,
$\alpha=\frac{1}{\rho} \frac{d \rho}{d T}$ – температурный коэффициент сопротивления, который
показывает относительное приращение сопротивления при увеличении температуры на один градус,
$\alpha$ может быть положительным и отрицательным. {B}=\frac{\rho}{4 \pi} \cdot \frac{B-A}{B \cdot A}$$
{B}=\frac{\rho}{4 \pi} \cdot \frac{B-A}{B \cdot A}$$
Ответ. $R=\frac{\rho}{4 \pi} \cdot \frac{B-A}{B \cdot A}$
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Какое количество витков проволоки (n) (удельное сопротивление ее равно
$\rho$=100 мк Ом•м, диаметр d=1 см) требуется накрутить
на фарфоровый цилиндр, имеющий радиус A=1 см, для того чтобы получить сопротивление R=8 Ом?
Решение. Основой для решения задачи будет формула для сопротивления вида:
$$R=\rho \frac{l}{S}(2.1)$$
Длину одного витка проволоки можно вычислить как:
$$l_{1}=2 \pi \cdot A(2.2)$$
Следовательно, длина всей проволоки (l) равна:
$$l=n \cdot 2 \pi \cdot A(2. {-2}}=100$$
{-2}}=100$$
Ответ. n=100
Читать дальше: Формула внутренней энергии.
сопротивление и удельное сопротивление | Физика
Цели обучения
К концу этого раздела вы сможете:
- Объяснять понятие удельного сопротивления.
- Используйте удельное сопротивление для расчета сопротивления определенных конфигураций материала.
- Используйте термический коэффициент удельного сопротивления для расчета изменения сопротивления в зависимости от температуры.
Зависимость сопротивления от материала и формы
Сопротивление объекта зависит от его формы и материала, из которого он состоит. Цилиндрический резистор на рисунке 1 легко анализировать, и таким образом мы можем получить представление о сопротивлении более сложных форм. Как и следовало ожидать, электрическое сопротивление цилиндра R прямо пропорциональна его длине L , подобно сопротивлению трубы потоку жидкости. Чем длиннее цилиндр, тем больше столкновений зарядов с его атомами произойдет. Чем больше диаметр цилиндра, тем больший ток он может пропускать (опять же аналогично потоку жидкости по трубе). На самом деле R обратно пропорционально площади поперечного сечения цилиндра A .
Чем длиннее цилиндр, тем больше столкновений зарядов с его атомами произойдет. Чем больше диаметр цилиндра, тем больший ток он может пропускать (опять же аналогично потоку жидкости по трубе). На самом деле R обратно пропорционально площади поперечного сечения цилиндра A .
Рис. 1. Однородный цилиндр длиной L и площадью поперечного сечения A. Его сопротивление потоку тока аналогично сопротивлению трубы потоку жидкости. Чем длиннее цилиндр, тем больше его сопротивление. Чем больше его площадь поперечного сечения А, тем меньше его сопротивление.
Для данной формы сопротивление зависит от материала, из которого состоит объект. Различные материалы оказывают различное сопротивление потоку заряда. Определим удельное сопротивление ρ вещества так, что сопротивление R объекта прямо пропорционально ρ . Удельное сопротивление ρ является внутренним свойством материала, не зависящим от его формы или размера. Сопротивление R однородного цилиндра длиной L , площадью поперечного сечения A , изготовленного из материала с удельным сопротивлением ρ , равно
Сопротивление R однородного цилиндра длиной L , площадью поперечного сечения A , изготовленного из материала с удельным сопротивлением ρ , равно
[латекс] R = \ frac{\rho L}{A }\\[/латекс].
В таблице 1 приведены репрезентативные значения ρ . Материалы, перечисленные в таблице, разделены на категории проводников, полупроводников и изоляторов на основе широких групп удельного сопротивления. Проводники имеют наименьшее удельное сопротивление, а изоляторы — наибольшее; полупроводники имеют промежуточное сопротивление. Проводники имеют разную, но большую плотность свободного заряда, в то время как большинство зарядов в изоляторах связаны с атомами и не могут свободно перемещаться. Полупроводники занимают промежуточное положение, имея гораздо меньше свободных зарядов, чем проводники, но обладая свойствами, из-за которых количество свободных зарядов сильно зависит от типа и количества примесей в полупроводнике. Эти уникальные свойства полупроводников используются в современной электронике, что будет рассмотрено в последующих главах.
| Материал | Удельное сопротивление ρ ( Ом ⋅ м ) |
|---|---|
| Проводники | |
| Серебро | 1. 59 × 10 −8 |
| Медь | 1. 72 × 10 −8 |
| Золото | 2. 44 × 10 −8 |
| Алюминий | 2. 65 × 10 −8 |
| Вольфрам | 5. 6 × 10 −8 |
| Железо | 9. 71 × 10 −8 |
| Платина | 10. 6 × 10 −8 |
| Сталь | 20 × 10 −8 |
| Свинец | 22 × 10 −8 |
| Манганин (сплав меди, марганца, никеля) | 44 × 10 −8 |
| Константан (сплав Cu, Ni) | 49 × 10 −8 |
| Меркурий | 96 × 10 −8 |
| Нихром (сплав Ni, Fe, Cr) | 100 × 10 −8 |
| Полупроводники [1] | |
| Углерод (чистый) | 3,5 × 10 5 |
| Углерод | (3,5 − 60) × 10 5 |
| Германий (чистый) | 600 × 10 −3 |
| Германий | (1−600) × 10 −3 |
| Кремний (чистый) | 2300 |
| Кремний | 0,1–2300 |
| Изоляторы | |
| Янтарный | 5 × 10 14 |
| Стекло | 10 9 − 10 14 |
| Люцит | >10 13 |
| Слюда | 10 11 − 10 15 |
| Кварц (плавленый) | 75 × 10 16 |
| Резина (твердая) | 10 13 − 10 16 |
| Сера | 10 15 |
| Тефлон | >10 13 |
| Дерево | 10 8 − 10 11 |
Пример 1.
 {-9{-5}\text{m}\end{массив}\\[/latex].
{-9{-5}\text{m}\end{массив}\\[/latex].
Обсуждение
Диаметр чуть меньше десятой доли миллиметра. Оно приводится только с двумя цифрами, потому что ρ известно только с двумя цифрами.
Изменение сопротивления в зависимости от температуры
Удельное сопротивление всех материалов зависит от температуры. Некоторые даже становятся сверхпроводниками (нулевое сопротивление) при очень низких температурах. (См. рис. 2.)
Рис. 2. Сопротивление образца ртути равно нулю при очень низких температурах — это сверхпроводник примерно до 4,2 К. Выше этой критической температуры ее сопротивление делает резкий скачок, а затем возрастает почти до линейно с температурой.
И наоборот, удельное сопротивление проводников увеличивается с повышением температуры. Поскольку атомы вибрируют быстрее и преодолевают большие расстояния при более высоких температурах, электроны, движущиеся через металл, совершают больше столкновений, что фактически увеличивает удельное сопротивление. При относительно небольших изменениях температуры (около 100ºC или менее) удельное сопротивление ρ изменяется с изменением температуры Δ T , как выражается в следующем уравнении
При относительно небольших изменениях температуры (около 100ºC или менее) удельное сопротивление ρ изменяется с изменением температуры Δ T , как выражается в следующем уравнении
ρ = ρ 0 (1 + α Δ T ),
где ρ 0 – исходное удельное сопротивление, а α – температурный коэффициент 0. (См. значения α в Таблице 2 ниже.) Для больших изменений температуры α может варьироваться, или может потребоваться нелинейное уравнение для нахождения ρ . Обратите внимание, что α положительно для металлов, что означает, что их удельное сопротивление увеличивается с температурой. Некоторые сплавы были разработаны специально, чтобы иметь небольшую температурную зависимость. Манганин (состоящий из меди, марганца и никеля), например, имеет α близок к нулю (до трех знаков по шкале в табл. 2), поэтому его удельное сопротивление слабо зависит от температуры.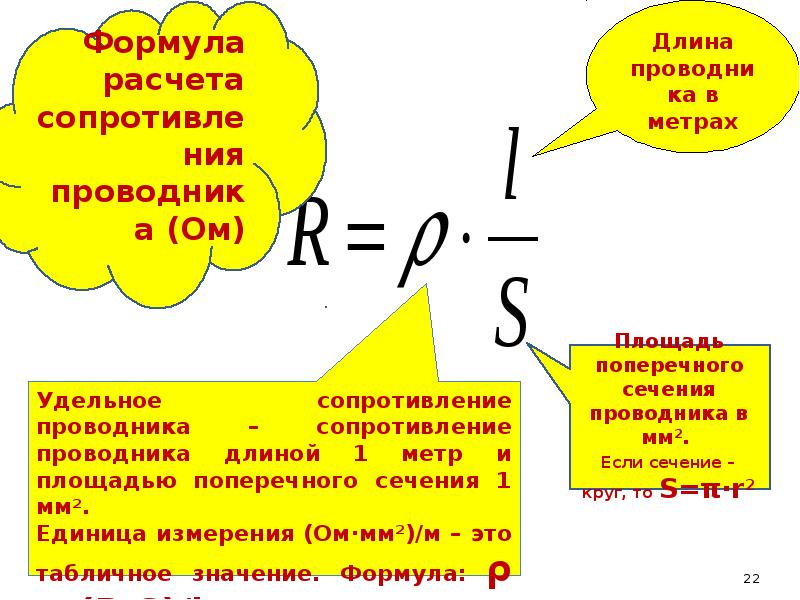 Это полезно, например, для создания эталона сопротивления, не зависящего от температуры.
Это полезно, например, для создания эталона сопротивления, не зависящего от температуры.
| Материал | Коэффициент (1/°C) [2] |
|---|---|
| Проводники | |
| Серебро | 3,8 × 10 −3 |
| Медь | 3,9 × 10 −3 |
| Золото | 3,4 × 10 −3 |
| Алюминий | 3,9 × 10 −3 |
| Вольфрам | 4,5 × 10 −3 |
| Железо | 5,0 × 10 −3 |
| Платина | 3,93 × 10 −3 |
| Свинец | 3,9 × 10 −3 |
| Манганин (сплав Cu, Mn, Ni) | 0,000 × 10 −3 |
| Константан (сплав Cu, Ni) | 0,002 × 10 −3 |
| Меркурий | 0,89 × 10 −3 |
| Нихром (сплав Ni, Fe, Cr) | 0,4 × 10 −3 |
| Полупроводники | |
| Углерод (чистый) | −0,5 × 10 −3 |
| Германий (чистый) | −50 × 10 −3 |
| Кремний (чистый) | −70 × 10 −3 |
Отметим также, что α является отрицательным для полупроводников, перечисленных в таблице 2, что означает, что их удельное сопротивление уменьшается с повышением температуры. Они становятся лучшими проводниками при более высокой температуре, потому что повышенное тепловое возбуждение увеличивает количество свободных зарядов, доступных для переноса тока. Это свойство уменьшения ρ с температурой также связано с типом и количеством примесей, присутствующих в полупроводниках. Сопротивление объекта также зависит от температуры, так как R 0 прямо пропорционально ρ . Для цилиндра мы знаем, что R = ρL / A , и поэтому, если L и A не сильно меняются с температурой, то R будет иметь такую же зависимость от температуры, как ρ . (Изучение коэффициентов линейного расширения показывает, что они примерно на два порядка меньше типичных температурных коэффициентов удельного сопротивления, поэтому влияние температуры на L and A is about two orders of magnitude less than on ρ .) Thus,
Они становятся лучшими проводниками при более высокой температуре, потому что повышенное тепловое возбуждение увеличивает количество свободных зарядов, доступных для переноса тока. Это свойство уменьшения ρ с температурой также связано с типом и количеством примесей, присутствующих в полупроводниках. Сопротивление объекта также зависит от температуры, так как R 0 прямо пропорционально ρ . Для цилиндра мы знаем, что R = ρL / A , и поэтому, если L и A не сильно меняются с температурой, то R будет иметь такую же зависимость от температуры, как ρ . (Изучение коэффициентов линейного расширения показывает, что они примерно на два порядка меньше типичных температурных коэффициентов удельного сопротивления, поэтому влияние температуры на L and A is about two orders of magnitude less than on ρ .) Thus,
R = R 0 ( 1 + α Δ T )
is the температурная зависимость сопротивления объекта, где R 0 — исходное сопротивление, R — сопротивление после изменения температуры Δ T . Многие термометры основаны на влиянии температуры на сопротивление. (См. рис. 3.) Одним из наиболее распространенных является термистор, полупроводниковый кристалл с сильной температурной зависимостью, сопротивление которого измеряется для получения его температуры. Устройство маленькое, поэтому быстро приходит в тепловое равновесие с той частью человека, к которой прикасается.
Многие термометры основаны на влиянии температуры на сопротивление. (См. рис. 3.) Одним из наиболее распространенных является термистор, полупроводниковый кристалл с сильной температурной зависимостью, сопротивление которого измеряется для получения его температуры. Устройство маленькое, поэтому быстро приходит в тепловое равновесие с той частью человека, к которой прикасается.
Рисунок 3. Эти известные термометры основаны на автоматизированном измерении сопротивления термистора в зависимости от температуры. (кредит: Biol, Wikimedia Commons)
Пример 2. Расчет сопротивления: сопротивление горячей нити
Хотя следует соблюдать осторожность при применении ρ = ρ 0 (1 + α Δ
и R = R 0 (1 + α Δ T ) для изменений температуры более 100ºC, для вольфрама уравнения работают достаточно хорошо для очень больших изменений температуры. Каково же тогда сопротивление вольфрамовой нити в предыдущем примере, если ее температуру повысить с комнатной (20°С) до типичной рабочей температуры 2850°С?
Стратегия
Это прямое применение R = R 0 (1 + α Δ T ), так как первоначальный сопротивление филосования было дано R303030303030303030303030303030303 0 = 0,350 Ом, а изменение температуры Δ T = 2830ºC. {-3}/º\text{C }\right)\left(2830º\text{C}\right)\right]\\ & =& {4.8\Omega}\end{массив}\\[/latex].
{-3}/º\text{C }\right)\left(2830º\text{C}\right)\right]\\ & =& {4.8\Omega}\end{массив}\\[/latex].
Обсуждение
Это значение согласуется с примером сопротивления фары в Законе Ома: сопротивление и простые схемы.
Исследования PhET: сопротивление в проводе
Узнайте о физике сопротивления в проводе. Измените его удельное сопротивление, длину и площадь, чтобы увидеть, как они влияют на сопротивление провода. Размеры символов в уравнении меняются вместе со схемой провода.
Нажмите, чтобы запустить симуляцию.
Резюме сечения
- Сопротивление R цилиндра длиной L и площадью поперечного сечения A равно [латекс]R=\frac{\rho L}{A}\\[/latex], где ρ — удельное сопротивление материала.
- Значения ρ в таблице 1 показывают, что материалы делятся на три группы: проводники, полупроводники и изоляторы .

- Температура влияет на удельное сопротивление; для относительно небольших изменений температуры Δ T , удельное сопротивление равно [латекс]\rho ={\rho }_{0}\left(\text{1}+\alpha \Delta T\right)\\[/latex] , где ρ 0 исходное удельное сопротивление, а [латекс]\текст{\альфа}[/латекс] — температурный коэффициент удельного сопротивления.
- В таблице 2 приведены значения для α , температурного коэффициента удельного сопротивления.
- Сопротивление R объекта также зависит от температуры: [латекс]R={R}_{0}\left(\text{1}+\alpha \Delta T\right)\\[/latex], где R 0 — исходное сопротивление, а R — сопротивление после изменения температуры.
Концептуальные вопросы
1. В каком из трех полупроводниковых материалов, перечисленных в таблице 1, примеси создают свободные заряды? (Подсказка: изучите диапазон удельного сопротивления для каждого из них и определите, имеет ли чистый полупроводник более высокую или более низкую проводимость. )
)
2. Зависит ли сопротивление объекта от пути прохождения тока через него? Рассмотрим, например, прямоугольный стержень — одинаково ли его сопротивление по длине и по ширине? (См. рис. 5.)
Рис. 5. Встречает ли ток, проходящий двумя разными путями через один и тот же объект, разное сопротивление?
3. Если алюминиевый и медный провода одинаковой длины имеют одинаковое сопротивление, какой из них имеет больший диаметр? Почему?
4. Объясните, почему [латекс]R={R}_{0}\left(1+\alpha\Delta T\right)\\[/latex] для температурного изменения сопротивления R объекта не так точен, как [латекс]\rho ={\rho }_{0}\left({1}+\alpha \Delta T\right)\\[/latex], что дает температурное изменение удельного сопротивления р .
Задачи и упражнения
1. Каково сопротивление отрезка медной проволоки 12-го калибра диаметром 2,053 мм длиной 20,0 м?
2. Диаметр медной проволоки нулевого калибра 8,252 мм. Найти сопротивление такого провода длиной 1,00 км, по которому осуществляется передача электроэнергии.
3. Если вольфрамовая нить диаметром 0,100 мм в электрической лампочке должна иметь сопротивление 0,200 Ом при 20ºC, то какой длины она должна быть?
4. Найти отношение диаметра алюминиевого провода к медному, если они имеют одинаковое сопротивление на единицу длины (как в бытовой электропроводке).
5. Какой ток протекает через стержень из чистого кремния диаметром 2,54 см и длиной 20,0 см, если к нему приложено напряжение 1,00 × 10 3 В? (Такой стержень можно использовать, например, для изготовления детекторов ядерных частиц). ? (б) Происходит ли это в бытовой электропроводке при обычных обстоятельствах?
7. Резистор из нихромовой проволоки используется в тех случаях, когда его сопротивление не может измениться более чем на 1,00% от его значения при 20,0ºC. В каком диапазоне температур его можно использовать?
8. Из какого материала изготовлен резистор, если его сопротивление при 100°С на 40,0% больше, чем при 20,0°С?
9. Электронное устройство, предназначенное для работы при любой температуре в диапазоне от –10,0ºC до 55,0ºC, содержит резисторы из чистого углерода. Во сколько раз увеличивается их сопротивление в этом диапазоне?
Во сколько раз увеличивается их сопротивление в этом диапазоне?
10. (a) Из какого материала сделан провод, если он имеет длину 25,0 м, диаметр 0,100 мм и сопротивление 77,7 Ом при 20,0ºC? б) Каково его сопротивление при 150°С?
11. При постоянном температурном коэффициенте удельного сопротивления, каково максимальное уменьшение сопротивления константановой проволоки в процентах, начиная с 20,0ºC?
12. Проволоку протягивают через матрицу, растягивая ее в четыре раза по сравнению с первоначальной длиной. Во сколько раз увеличивается его сопротивление?
13. Медный провод имеет сопротивление 0,500 Ом при 20,0°С, а железный провод имеет сопротивление 0,525 Ом при той же температуре. При какой температуре их сопротивления равны?
14. (a) Цифровые медицинские термометры определяют температуру путем измерения сопротивления полупроводникового устройства, называемого термистором (которое имеет α = –0,0600/ºC), когда оно имеет ту же температуру, что и пациент. Какова температура тела пациента, если сопротивление термистора при этой температуре составляет 82,0% от его значения при 37,0°С (нормальная температура тела)? (b) Отрицательное значение для α может не сохраняться при очень низких температурах. Обсудите, почему и так ли это, здесь. (Подсказка: сопротивление не может стать отрицательным.)
Какова температура тела пациента, если сопротивление термистора при этой температуре составляет 82,0% от его значения при 37,0°С (нормальная температура тела)? (b) Отрицательное значение для α может не сохраняться при очень низких температурах. Обсудите, почему и так ли это, здесь. (Подсказка: сопротивление не может стать отрицательным.)
15. Комплексные концепции (a) Повторите упражнение 2 с учетом теплового расширения вольфрамовой нити. Вы можете принять коэффициент теплового расширения равным 12 × 10 −6 /ºC. б) На сколько процентов ваш ответ отличается от ответа в примере?
16. Необоснованные результаты (a) До какой температуры нужно нагреть резистор, сделанный из константана, чтобы удвоить его сопротивление при постоянном температурном коэффициенте удельного сопротивления? б) Разрезать пополам? в) Что неразумного в этих результатах? (d) Какие предположения неразумны, а какие предпосылки противоречивы?
Сноски
- 1 Значения сильно зависят от количества и типов примесей
- 2 Значения при 20°C.

Глоссарий
- Удельное сопротивление:
- внутреннее свойство материала, не зависящее от его формы или размера, прямо пропорциональное сопротивлению, обозначаемое ρ
- Температурный коэффициент удельного сопротивления:
- эмпирическая величина, обозначаемая α , которая описывает изменение сопротивления или удельного сопротивления материала при температуре
Выбранные решения для проблем и упражнений
1. 0,104 ω
3. 2,8 × 10 −2 M
5. 1,10 × 10 -3 A
7. -5ºC до 45ºC
9. 1,03
11. 0,06%
13,-17ºC
15. (а) 4,7 Ом (суммарно) (б) уменьшение на 3,0%
- Значения сильно зависят от количества и типа примесей °С. ↵
Значение сопротивления проводника и способ его расчета
В этой части серии «Практикующий техник» мы рассмотрим расчеты, необходимые для определения сопротивления данного проводника. Этот часто упускаемый из виду параметр может быть важен при попытке определить подходящий диаметр проволоки для данного применения. Также важно учитывать сопротивление проводника при оценке эффективности применения. Меньшее сопротивление означает меньшее рассеивание мощности проводником. Оптимизация этих двух аспектов сопротивления проводника для вашего конкретного приложения может привести к значительному снижению затрат на внедрение и эксплуатацию. Важно знать сопротивление, предлагаемое данным проводником, а также понимать, в какой степени это сопротивление влияет на приложение и его работу. По этой причине мы рассмотрим некоторые важные аспекты сопротивления проводника, кратко опишем и обсудим их.
Этот часто упускаемый из виду параметр может быть важен при попытке определить подходящий диаметр проволоки для данного применения. Также важно учитывать сопротивление проводника при оценке эффективности применения. Меньшее сопротивление означает меньшее рассеивание мощности проводником. Оптимизация этих двух аспектов сопротивления проводника для вашего конкретного приложения может привести к значительному снижению затрат на внедрение и эксплуатацию. Важно знать сопротивление, предлагаемое данным проводником, а также понимать, в какой степени это сопротивление влияет на приложение и его работу. По этой причине мы рассмотрим некоторые важные аспекты сопротивления проводника, кратко опишем и обсудим их.
Какие факторы определяют сопротивление данного проводника?
Есть три фактора, которые определяют величину сопротивления данного проводника. Они проиллюстрированы здесь в соотношении, используемом для расчета сопротивления проводника.
Мы начнем с признания того очевидного факта, что длина проводника влияет на его общее сопротивление. Чем больше длина данного проводника, тем большее сопротивление будет иметь этот проводник. Это хорошо видно из соотношения, приведенного выше.
Чем больше длина данного проводника, тем большее сопротивление будет иметь этот проводник. Это хорошо видно из соотношения, приведенного выше.
Удельное сопротивление материала проводника играет важную роль в общем сопротивлении. Это связано с тем, что разные материалы, например золото или медь, обладают разным сопротивлением постоянному току. Материалы проводников, как правило, выбираются на основе рентабельности и пригодности. Удельное сопротивление материала некоторых из наиболее распространенных проводников, используемых сегодня, указано ниже.
Последним важным фактором, определяющим сопротивление проводника, является площадь поперечного сечения данного проводника. Важно отметить обратную зависимость между площадью поперечного сечения проводника и сопротивлением проводника. Как видно из приведенного примера, чем меньше площадь поперечного сечения проводника, тем больше становится значение сопротивления проводника. Это означает, что, хотя использование меньших размеров проводника может быть дешевле, существует компромисс с сопротивлением.