Фронтальная косоугольная диметрическая проекция — Немного о ремонте и строительстве

Во фронтальной косоугольной диметрической проекции принято следующее положение аксонометрических осей: ось ох направлена горизонтально; ось оу — под углом 45° к оси ох и ось oz — вертикально . По этим осям и направляться вести построение фронтальной проекции предмета. Допускается использовать «левое» размещение осей.

Линейные размеры, параллельные оси оу, откладывают в масштабе, в два раза меньшем, чем по осям ох и oz. Основным для этого вида аксонометрических проекций есть то, что фигуры, параллельные фронтальной плоскости проекций V, изображаются без искажений.

Исходя из этого такие аксонометрические проекции и именуются фронтальными. Построение фронтальной проекции постоянно начинают с нанесения осей, каковые выполняют узкими целыми линиями.

Последовательность построения фронтальных проекций некоторых фигур продемонстрирована на рис. 2.

Рис. 1. Положение аксонометрических осей: а — «правое»; б — «левое».

В случае если расположить ось вращения цилиндра параллельно оси oz либо ох, то его основания проецируются в виде эллипсов.

Фронтальная диметрическая проекция куба с вписанными в его грани окружностями изображена на рис. 34.

Окружность, расположенная на передней грани куба, изображается без искажений, а окружности, расположенные на верхней и боковой гранях, изображаются в виде эллипсов однообразной размеров и формы.

Для построения эллипса на гранях находят восемь точек, каковые после этого медлено соединяют по лекалу. Четыре точки определяются сходу — это середины сторон параллелограммов, изображающих грани куба.

Четыре другие точки определяются на диагоналях параллелограммов методом переноса их с диагоналей квадрата.

Для построения эллипса на верхней грани сперва на передней грани куба отмечают пересечения 1 и 2 точки диагоналей квадрата с окружностью. После этого из этих точек выполняют прямые параллельно оси oz до верхнего ребра куба (верхней стороны квадрата).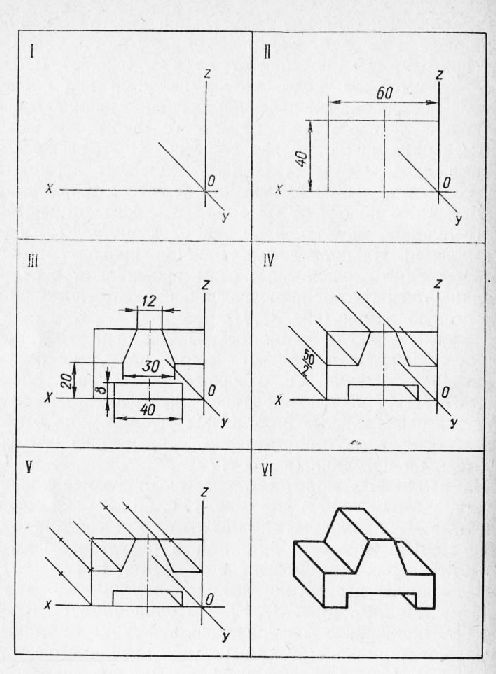

Из взятых на ребре точек выполняют прямые параллельно оси оу до пересечения их с диагоналями параллелограмма. Это и будут точки эллипса.

Рис. 2. Последовательность построения фронтальной косоугольной диметрической проекции: а — куба; б — цилиндра; 8 — шестигранной призмы.

Рис. 3. Фронтальная днметрическая проекция куба с вписанными в его грани окружностями.

Подобно находят диагональные точки при построении эллипса на боковой грани куба. Соединив отысканные точки плавной кривой по лекалу, возьмём эллипсы.

Угол наклона громадной оси эллипса равен приблизительно 7° по отношению к оси ох, в случае если эллипс изображает окружность на верхней грани куба, и по отношению к оси oz, в случае если эллипс изображает окружность на боковой грани куба. Малую ось эллипса располагают перпендикулярно большой.

На практике при построении фронтальных проекций подробностей цилиндрической формы в большинстве случаев вычерчивают не эллипсы, а овалы. Форма овала близка к форме эллипса, но вычертить его более легко, поскольку построение делают циркулем правильно сопряжений.

Рис. 4. Построение овала на верхней грани куба.

Рис. 5. Прямоугольные проекции модели.

Овал на верхней грани куба строят следующим образом: – выполняют аксонометрические оси ох, оу и oz; после этого из центра О — окружность диаметром, равным диаметру окружности, изображенной на рис. 34; – выполняют громадную ось овала под углом 7° к оси ох и перпендикулярно к ней малую ось.

Продолжение малой оси пересекает окружность в точках направляться1 и 02; – из точек Oi и,02, как из центров, выполняют вспомогательные дуги радиусом 001 равным 002, до пересечения с продолжением малой оси в точках 03 и 04, являющихся центрами громадных дуг овала; – выполняют прямые 04Л и 03В, каковые пересекут громадную ось овала в точках 06 и Ов, являющихся центрами малых дуг овала; – из центров 03 и 04 выполняют громадные дуги овалов радиусом 04А, равным 03В; – из центров 08 и 06 выполняют малые дуги, замыкающие овал, радиусом ОьА, равным ОйВ.

Построение овала — приближенного изображения окружности — в профильной плоскости подобное.

Разглядим построение фронтальной диметрической проекции модели по чертежу, приведенному на рис. 5. Сперва выполняют оси проекций ох, оу и oz.

самый характерным видом модели есть вид спереди, исходя из этого построение фронтальной проекции начинают с вычерчивания в плоскости осей ох—oz для того чтобы же изображения, каким есть вид спереди. В данной плоскости узкими, чуть заметными линиями намечают прямоугольник, соответствующий громаднейшей высоте и ширине модели.

Для этого по оси ох от точки о влево откладывают 60 мм (ширина модели), а по оси oz вверх — 40 мм (высота модели). Из взятых отметок выполняют прямые, соответственно параллельные осям проекции ох и oz.

Посередине габаритного прямоугольника выполняют вертикальную осевую линию.

По отношению к данной осевой линии в габаритном прямоугольнике вычерчивают контур модели, соответствующий очертанию ее изображения на виде спереди. Из угловых точек вычерченного контура выполняют параллельные прямые под углом 45° по отношению к оси ох, соответствующие направлению оси оу во фронтальной проекции.

На наклонных прямых откладывают размер толщины модели, уменьшенной вдвое, т. е. 50 : 2 = 25 мм. Полученные на наклонных прямых отметки соединяют последовательно прямыми линиями, в следствии чего приобретают изображение модели во фронтальной проекции.

Все указанные построения делают узкими, чуть заметными линиями. По окончании построения обводят полученное изображение контурными линиями и удаляют линии и линии построения невидимого контура.

Рис. 6. Последовательность построения фронтальной димет-рической проекции модели.

Рис. 7. Последовательность построения фронтальной диметрической проекции кронштейна.

Лекция 14 | Начертательная Геометрия | ОмГТУ | Лекториум

Вы прочитали статью, но не прочитали журнал…

• Разметка окружностей, центров и отверстий в слесарном деле

• Приемы плоскостной разметки

• Инструкционная карта 2

• Конструкция отливки

Фронтальная косоугольная диметрическая и прямоугольная изометрическая проекции

Похожие презентации:

Основы архитектуры и строительных конструкций. Основы проектирования

Конструктивные схемы многоэтажных зданий

Стадии проектирования зданий. Маркировка строительных чертежей (лекция №2)

Правила выполнения архитектурно-строительных чертежей

ЕСКД. Общие правила оформления чертежей. (Лекция 1.1)

задачи на построение (геометрия 7 класс)

Выполненный вариант контрольной работы по разделу «Техническое черчение». (Приложение 3)

Параллельность в пространстве. (Графическая работа 2)

Строительное черчение. Графическое оформление и чтение строительных чертежей

Правила оформления чертежей ЕСКД. Форматы, масштабы, линии, шрифты

Фронтальная косоугольная диметрическая и
прямоугольная изометрическая проекции
Аксонометрической проекцией называется изображение, полученное на
аксонометрической плоскости в результате параллельного проецирования
предмета вместе с системой координат, которое наглядно отображает его форму.
Аксонометрия (от греч. аxon – ось и metreo – измеряю) измерение по осям.
Можно ли представить форму предметов по наглядному изображению?
Аксонометрические проекции относят к наглядным изображениям.
а)
б)
а) диметрическая проекция
б) изометрическая проекция
а)
б)
а) перспективное изображение с одной точкой схода
б) перспективное изображение с двумя точками схода
Оси диметрической проекции располагаются так: x — горизонтально, z –
вертикально, y – под углом 45º
При построении осей изометрической проекции ось z расположена вертикально,
а оси x и y составляют с ней углы равные 120º
Построение изометрических осей происходит так:
На вертикальной оси z
берем точку О и проводим
дугу произвольного
радиуса R
Из точки пересечения дуги
с продолжением оси z
проводим дугу того же
радиуса до пересечения с
первой дугой в точках 1 и 2
Соединив точку О с
точками 1 и 2 получаем
направление осей x и y
• ось z всегда вертикальна
• все измерения выполняются только по
аксонометрическим осям или прямым,
параллельным им
• все прямые линии, параллельные друг другу или
осям координат на комплексном чертеже, в
аксонометрических проекциях остаются
параллельными между собой и
соответствующим аксонометрическим осям
Вдоль оси x и параллельно ей откладывают высоты, а вдоль y –
сокращенный в два раза размер ширины натуральный размер
длины предмета, вдоль z – натуральный размер ее
По всем аксонометрическим осям и параллельно им в
изометрической проекции откладывают натуральные размеры
Чаще всего построение аксонометрической проекции происходит с
построения основания.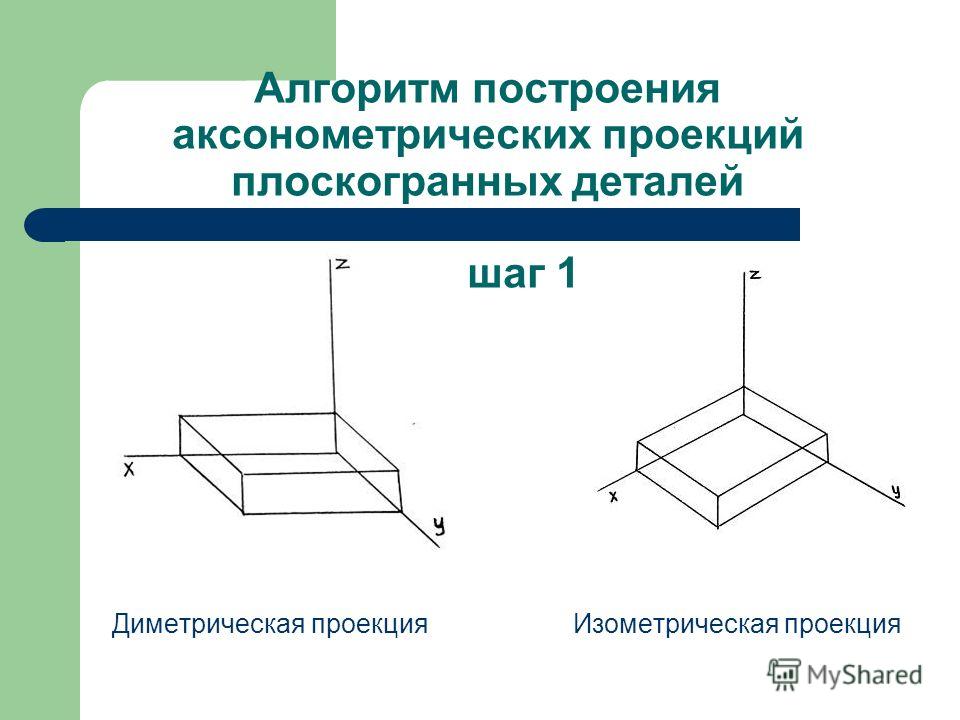
Рассмотрим алгоритм построения
аксонометрических проекций предмета на
примере прямоугольного
параллелепипеда
Построение осей аксонометрических проекций и нижнего
основания прямоугольного параллелепипеда
Шаг 1
Диметрическая проекция
Изометрическая проекция
Построение вертикальных ребер
Шаг 2
Диметрическая проекция
Изометрическая проекция
Построение боковых граней и верхнего основания
Шаг 3
Диметрическая проекция
Изометрическая проекция
Шаг 4 Определение видимости граней
Шаг 5 Обводка
Диметрическая проекция
Изометрическая проекция
Запомните!!!
В аксонометрических проекциях из каждой
вершины предмета всегда выходят три ребра
(видимых или невидимых).
Шаг 1
Диметрическая проекция
Изометрическая проекция
Шаг 2
Диметрическая проекция
Изометрическая проекция
Шаг 3
Диметрическая проекция
Изометрическая проекция
Шаг 4
Диметрическая проекция
Изометрическая проекция
Шаг 5
Диметрическая проекция
Изометрическая проекция
Размеры на изображении детали наносят так, чтобы цифровые значения
«лежали» в плоскостях V, H и W

English    
Русский
Правила

геометрия — являются ли косые проекции одним из конкретных подразделений триметрических проекций?

К сожалению, у меня нет 50 представителей, чтобы оставить свой ответ в качестве комментария, поэтому я сделаю это здесь.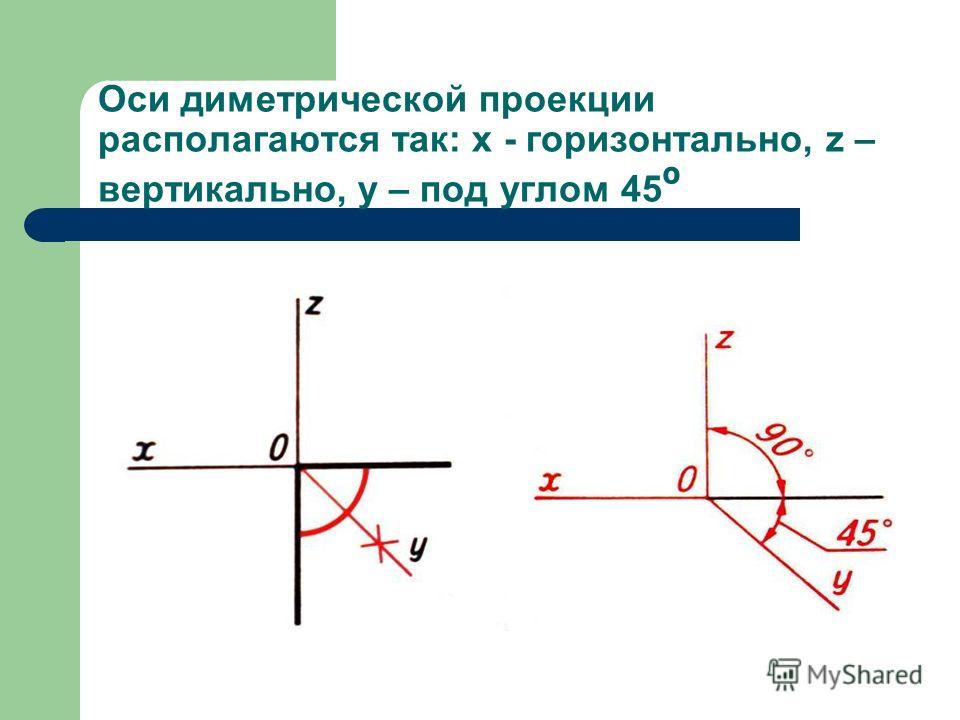 В любом случае, это, вероятно, более уместно сделать здесь.

Ответ

Держу пари, что некоторые , не все косых проекций являются подмножествами диметрической проекции, и что по крайней мере одна из них является подмножеством триметрической проекции.

Помещение

Описательно, согласно графику проекционной сетки Википедии, диметрическая проекция (конгруэнтность двух углов) содержит третий луч, который делит пополам дополнительный угол, определяемый двумя другими лучами. Это устанавливает основу и определяет трехмерное пространство, хотя и в двухмерной плоскости просмотра.

В этом примере Диметрика главный угол равен $150°$, дополнительный угол равен $210°$, а два угла, разделенные пополам из дополнительного угла третьим лучом, равны $105°$.

Для моделей Military и Cavalier основной угол составляет 9 долларов США.0°$ (одна из базовых плоскостей параллельна плоскости наблюдения, с определяющими лучами по диагонали (военный) или параллельными/перпендикулярными (кавалер)), оба дополнительных угла равны $270°$, а оба угла, разделенные пополам, равны $135°$ .

На первый взгляд может показаться, что пример сверху вниз не является диметрическим, если вы начнете с проверки самого нижнего угла $90°$ в качестве основного. Однако это действительно диметрический угол, если вы считаете крайний правый угол $180°$ основным. Дополнительный угол в этом случае равен основному углу, $180°$, и при делении пополам получается два конгруэнтных, прямых, $9углы 0°$.

Википедия также указывает проекцию кабинета как диагональную проекцию в своей записи 3D Projection. Требование, предъявляемое к этой проекции, состоит в том, что одна из граней отображаемого объекта, не обязательно базовая плоскость, должна быть параллельна плоскости просмотра. Кроме того, кажется, что все лучевые углы разные, а это означает, что проекция Cabinet может считаться подмножеством проекции Trimetric (соответствие 0 углов).

Следовательно, поскольку наклонная проекция кабинета напоминает триметрическую проекцию, а наклонная военная, кавалерская и нисходящая проекции напоминают диметрическую проекцию, я не думаю, что мы можем утверждать, что все косые проекции являются триметрическими (или диметрическими для это важно).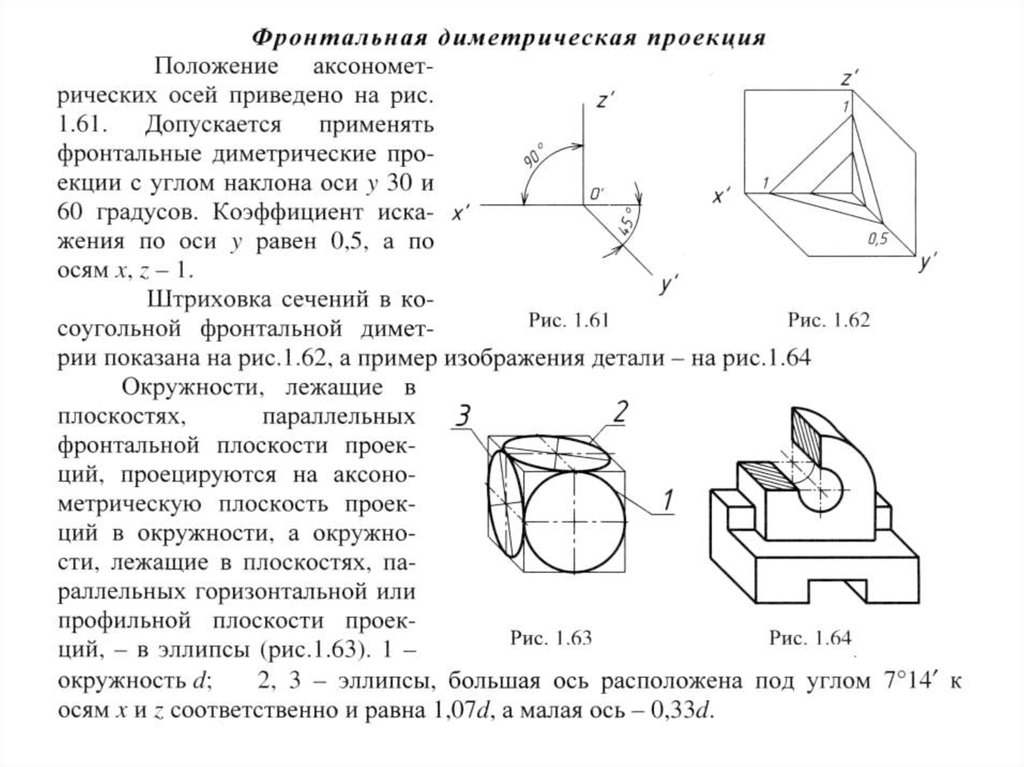

Перегиб

Я думаю, что решающим выбором для различения обычных косых проекций от аксонометрических является то, что для наклонной диметрической проекции по крайней мере один из углов между базисными векторами является целым числом, кратным $90°$ / $π/4$: не менее $90°$ / $π/4$ и не более $2 \cdot 90°$ или $180°$ / $2 \cdot π/4$ или $\pi/2$. Аксонометрические Диметрические проекции могут иметь первичный угол любого значения (по-видимому, между $\pi/4$ и $\pi/2$), где дополнение по-прежнему делится пополам, образуя 2 оставшихся конгруэнтных угла.

Для проекций «Военная» и «Кавалерская» выбор основного угла — правильный, или $π/4$. Для Top-Down выбор прямой или $π/2$.

Теоретически мы могли бы придумать другие проекции, в которых выбор основного угла был бы острым, $<π/4$, или рефлекторным, $>π/2$. Не похоже, чтобы многие источники в Интернете использовали эти формы проекций, вероятно, потому, что они настолько искажают формы, что они выглядят несовместимыми с реальностью и из работ типа М.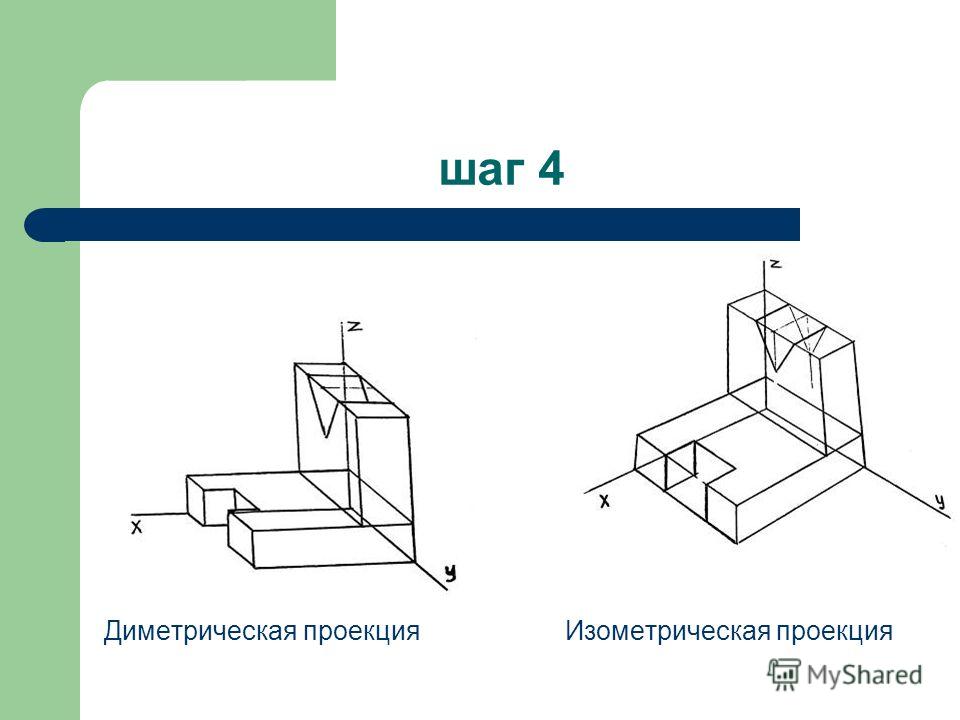 К. Эшера, или потому, что они искажают математику.

Это обсуждение даже не касается масштабирования базисных векторов, кроме ориентации/направления, поэтому я уверен, что вы могли бы добавить дополнительные классификации: один класс для трех конгруэнтных* базисных векторов, один класс для двух конгруэнтных базисных векторов и 1 разной длины и один класс для трех базисных векторов разной длины.

*: В смысле конгруэнтных отрезков, описанных в первой аксиоме конгруэнтности Гильберта. Кажется, я не могу найти термин, описывающий векторы равной величины. Параллельность и антипараллельность, по-видимому, описывают векторы в одном и том же или противоположном направлении друг к другу, в то время как коллинеарность описывает векторы, лежащие вдоль одной и той же линии в пространстве, обязательно параллельные или антипараллельные. Конгруэнтность в других контекстах может означать равенство всех компонентов более крупного абстрактного объекта, относящегося к величинам и углам, например, как равностороннее относится к равным величинам сегментов, составляющих форму, но не к самим величинам сегментов. В качестве замены может служить эквивалентность, например, как некоторые источники предлагают сонаправленность вместо анти-/параллельности, но это, вероятно, требует другой публикации на English или Math Stack Exchange.

Параллельная (ортогональная и наклонная) проекция в компьютерной графике

Проекция — это явление, которое используется в компьютерной графике для отображения вида трехмерного объекта на проецируемой панели дисплея, где объем просмотра определяется мировой координатой и затем сопоставьте эти мировые координаты с портом просмотра.

Проекция следующего типа:
 

  а) Параллельная проекция б) Перспективная проекция  

Параллельная проекция : Параллельная проекция — это разновидность проекции, в которой проекционные линии выходят параллельно из поверхности многоугольника и затем падают параллельно на плоскость. В параллельной проекции центр проекции лежит в бесконечности.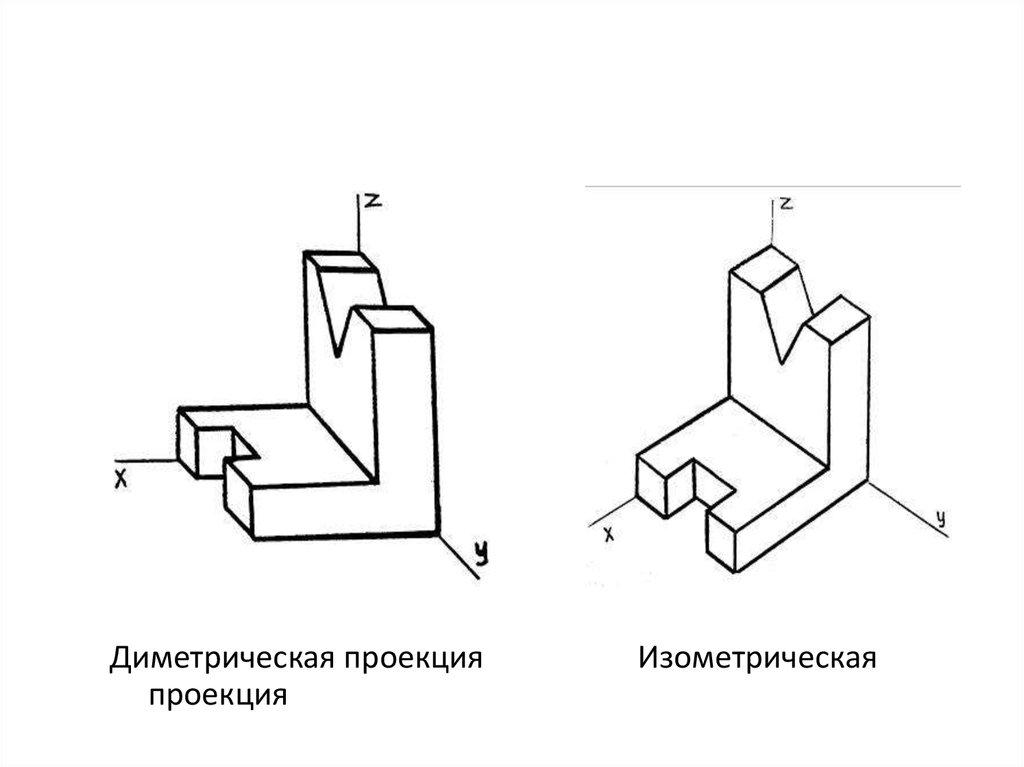 В параллельной проекции вид объекта, полученный на плоскости, менее реалистичен, так как отсутствует недостаток. и относительная размерность объекта остается неизменной.

Параллельная проекция делится на две категории:

  а) Ортогональная проекция 
  b) Косая проекция  

(a) Орфографическая проекция: Это вид параллельной проекции, в которой линии проекции выходят параллельно из поверхности объекта и падают перпендикулярно плоскости проекции.

Орфографическая проекция бывает двух категорий:

(a).1. Мультиракурсная проекция: Далее она делится на три категории –

(1) Вид сверху: В этой проекции наблюдаются лучи, исходящие из верхней части поверхности многоугольника.

2) Вид сбоку : Это еще один тип проекции ортогональной проекции, при которой наблюдается боковой вид поверхности многоугольника.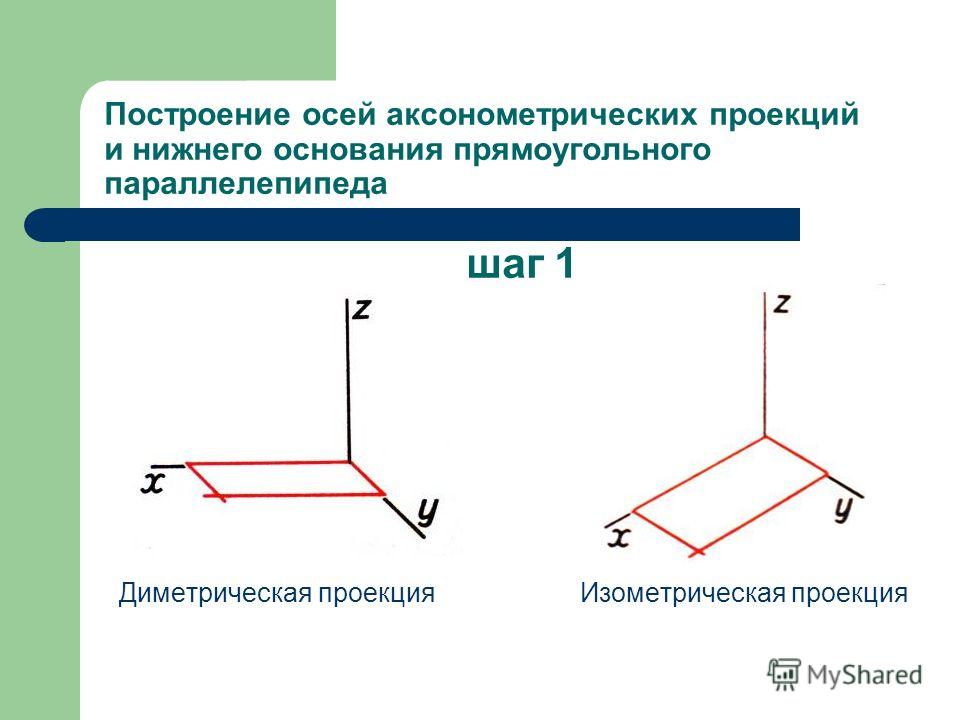

3) Вид спереди : В этой ортогональной проекции наблюдается вид спереди объекта.
 

несколько сторон.

Далее он делится на три категории:

(1) Изометрическая проекция: Это метод визуального представления трехмерных объектов в двухмерном отображении на технических и инженерных чертежах. Здесь, в этой проекции, три оси координат кажутся одинаково укороченными, а угол между любыми двумя из них составляет 120 градусов.

(2) Диметрическая проекция : Это разновидность ортогональной проекции, при которой визуализируемый объект имеет только две смежные стороны и углы равны.

(3) Триметрическая проекция : Это разновидность ортогональной проекции, при которой все смежные стороны и углы визуализируемого объекта кажутся неравными.

(b) Косая проекция : Это разновидность параллельной проекции, в которой лучи, исходящие из поверхности многоугольника, выходят параллельно и падают под углом, отличным от 90 градусов в самолете.