Онлайн калькулятор: Объем геометрических фигур

УчебаМатематикаГеометрия

Рассчитывает объем геометрических фигур (куб, призма, пирамида, усеченная пирамида, конус, цилиндр, сфера, эллипсоид, тороид).

Данная статья содержит калькуляторы для расчета объема различных геометрических фигур. Основной источник формул: Spiegel, Murray R. Mathematical Handbook of Formulas and Tables. Schaum’s Outline series in Mathematics. McGraw-Hill Book Co., 1968.

Объем куба

Размеры куба

Формула:

Объем куба

Сторона (H)

Длина ребра куба (H)

Точность вычисления

Знаков после запятой: 5

Объем

 

Объем прямоугольной призмы

Размеры прямоугольной призмы

Формула:

Объем прямоугольной призмы

Ширина (W)

Высота (H)

Высота (H)

Длина (L)

Точность вычисления

Знаков после запятой: 5

Объем

 

Объем пирамиды

Размеры пирамиды

Формула:

Объем пирамиды

Площадь основания (Sb)

Площадь основания

Высота (H)

Высота (H)

Точность вычисления

Знаков после запятой: 5

Объем

 

Объем усеченной пирамиды

Размеры усеченной пирамиды

Формула:

Объем усеченной пирамиды

Площадь первого основания (Sb1)

Площадь второго основания (Sb2)

Высота (H)

Высота (H)

Точность вычисления

Знаков после запятой: 5

Объем

 

Объем конуса

Размеры конуса

Формула:

Объем конуса

Радиус (R)

Высота (H)

Высота (H)

Точность вычисления

Знаков после запятой: 5

Объем

 

Объем цилиндра

Размеры цилиндра

Formula:

Объем цилиндра

Высота (H)

Высота (H)

Радиус (R)

Точность вычисления

Знаков после запятой: 5

Объем

 

Объем сферы

Размеры сферы

Формула:

Объем сферы

Радиус (R)

Точность вычисления

Знаков после запятой: 5

Объем

 

Объем эллипсоида

Размеры эллипсоида

Формула:

Объем эллипсоида

Радиус 1 (R1)

Радиус 2 (R2)

Радиус (R3)

Точность вычисления

Знаков после запятой: 5

Объем

 

Объем тороида

Размеры тороида

Формула:

Объем тора

Радиус 1 (R1)

Радиус 2 (R2)

Точность вычисления

Знаков после запятой: 5

Объем

 

Ссылка скопирована в буфер обмена

Похожие калькуляторы

• • Куб
• • Конус
• • Тор
• • Объем сегмента цилиндра
• • Объем жидкости в прямоугольном баке под наклоном
• • Раздел: Геометрия ( 94 калькуляторов )

 #геометрия #объем Геометрия Инженерные конус куб Математика объем пирамида прямоугольная призма сфера тор тороид усеченная пирамида цилиндр эллипсоид

 PLANETCALC, Объем геометрических фигур

Anton2020-11-03 14:19:26

Калькулятор расчета объема груза — Avrora Logistic

• На главную

• Расписание
  движения

• КАЛЬКУЛЯТОР
  ТАМОЖЕННЫХ
  ПЛАТЕЖЕЙ

• КАЛЬКУЛЯТОР
  СБОРНЫХ
  ГРУЗОВ

• КАЛЬКУЛЯТОР
  ЦЕЛЫХ
  КОНТЕЙНЕРОВ

• РАСЧЕТ ОБЪЕМА
  ГРУЗА

Рассчитайте объем вашего груза

РАСЧЕТ ОБЪЕМА ГРУЗА

ШИРИНА (W) *

ДИАМЕТР (D) *

РАСЧЕТ ОБЪЕМА

КоробкиЦилиндр

ВЫСОТА (H) *

ЕДИНИЦА ИЗМЕРЕНИЯ *

ммсмм

ДЛИНА (L) *

КОЛИЧЕСТВО КОРОБОК *

КОЛИЧЕСТВО ЦИЛИНДРОВ *

ИТОГО:

Объем одной коробки Объем одного цилиндра	0 м³
Общий объем	0 м³

ИСПОЛЬЗУЙТЕ ПОЛУЧЕННЫЕ РАСЧЕТЫ
ДЛЯ ОФОРМЛЕНИЯ ЗАЯВКИ

Далее

• 
  
  
  На главную
  
• 
  
  
  Расписание
  движения
  
• 
  
  
  РАСЧЕТ ОБЪЕМА
  ГРУЗА
  




• 
  
  
  КАЛЬКУЛЯТОР
  
  ТАМОЖЕННЫХ
  
  ПЛАТЕЖЕЙ
  
• 
  
  
  КАЛЬКУЛЯТОР
  
  СБОРНЫХ
  
  ГРУЗОВ
  
• 
  
  
  КАЛЬКУЛЯТОР
  
  ЦЕЛЫХ
  
  КОНТЕЙНЕРОВ
  

Возникли вопросы?

Я согласен на обработку персональных данных в порядке и на условиях, указанных по ссылке

Прикрепить файл (максимальный размер 20 Мб)

Калькулятор объема

Ниже приведен список калькуляторов объема для нескольких распространенных форм. Пожалуйста, заполните соответствующие поля и нажмите кнопку «Рассчитать».

Калькулятор объема сферы

Калькулятор объема конуса

Калькулятор объема куба

Калькулятор объема цилиндра

Калькулятор объема прямоугольного резервуара

Длина (л) милиярдыфутыдюймыкилометрыметрысантиметрымиллиметрымикрометрынанометрыангстремы Ширина (ш) милиярдыфутыдюймыкилометрыметрысантиметрымиллиметрымикрометрынанометрыангстремы Высота (ч) милиярдыфутыдюймыкилометрыметрысантиметрымиллиметрымикрометрынанометрыангстремы

Калькулятор объема капсулы

Калькулятор объема сферической крышки

Для расчета укажите любые два значения ниже.

Базовый радиус (r) милиярдыфутыдюймыкилометрыметрысантиметрымиллиметрымикрометрынанометрыангстремы Радиус шара (R) милиярдыфутыдюймыкилометрыметрысантиметрымиллиметрымикрометрынанометрыангстремы Высота (ч) милиярдыфутыдюймыкилометрыметрысантиметрымиллиметрымикрометрынанометрыангстремы

Калькулятор объема усеченного конуса

Верхний радиус (r) милиярдыфутыдюймыкилометрыметрысантиметрымиллиметрымикрометрынанометрыангстремы Радиус дна (R) милиярдыфутыдюймыкилометрыметрысантиметрымиллиметрымикрометрынанометрыангстремы Высота (h) милиярдыфутыдюймыкилометрыметрысантиметрымиллиметрымикрометрынанометрыангстремы

Калькулятор объема эллипсоида

Ось 1 (a) милиярдыфутыдюймыкилометрыметрысантиметрымиллиметрымикрометрынанометрыангстремы Ось 2 (b) милиярдыфутыдюймыкилометрыметрысантиметрымиллиметрымикрометрынанометрыангстремы Ось 3 (c) милиярдыфутыдюймыкилометрыметрысантиметрымиллиметрымикрометрынанометрыангстремы

Калькулятор объема квадратной пирамиды

Калькулятор объема пробирки

Внешний диаметр (d1) милиярдыфутыдюймыкилометрыметрысантиметрымиллиметрымикрометрынанометрыангстремы Внутренний диаметр (d2) милиярдыфутыдюймыкилометрыметрысантиметрымиллиметрымикрометрынанометрыангстремы Длина (л) милиярдыфутыдюймыкилометрыметрысантиметрымиллиметрымикрометрынанометрыангстремы

Связанные Калькулятор площади поверхности | Калькулятор площади

Объем – это количественная оценка трехмерного пространства, занимаемого веществом.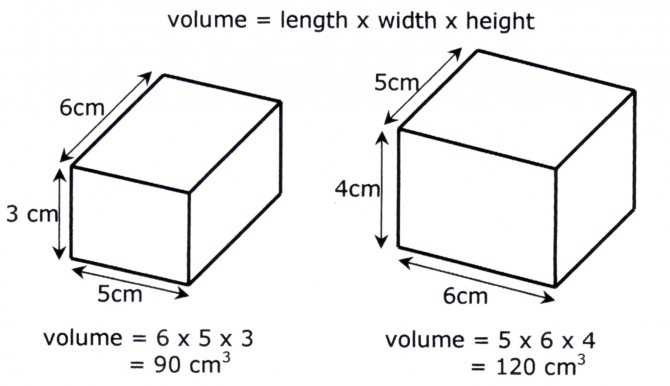 Единицей объема в системе СИ является кубический метр, или 9.0253 м ³ . По соглашению объем контейнера обычно представляет собой его вместимость и количество жидкости, которое он может вместить, а не объем пространства, которое вытесняет фактический контейнер. Объемы многих форм можно рассчитать с помощью четко определенных формул. В некоторых случаях более сложные формы можно разбить на более простые совокупные формы, и сумма их объемов используется для определения общего объема. Объемы других, еще более сложных форм, можно рассчитать с помощью интегрального исчисления, если существует формула для границы формы. Помимо этого, формы, которые не могут быть описаны известными уравнениями, могут быть оценены с использованием математических методов, таких как метод конечных элементов. В качестве альтернативы, если плотность вещества известна и однородна, объем можно рассчитать, используя его вес. Этот калькулятор вычисляет объемы для некоторых из наиболее распространенных простых форм.

Сфера

Сфера — это трехмерный аналог двумерного круга. Это идеально круглый геометрический объект, который математически представляет собой набор точек, равноудаленных от заданной точки в его центре, где расстояние между центром и любой точкой на сфере равно радиусу r . Вероятно, наиболее известным сферическим объектом является идеально круглый шар. В математике существует различие между шаром и сферой, где шар представляет собой пространство, ограниченное сферой. Независимо от этого различия, шар и сфера имеют одинаковый радиус, центр и диаметр, и вычисление их объемов одинаково. Как и в случае с окружностью, самый длинный отрезок, соединяющий две точки сферы через ее центр, называется диаметром, д . Уравнение для расчета объема сферы приведено ниже:

объем =

πr 3

EX: Клэр хочет наполнить идеально сферический водяной шар радиусом 0,15 фута уксусом, чтобы использовать его в битве с водяным шаром против ее заклятого врага Хильды в ближайшие выходные.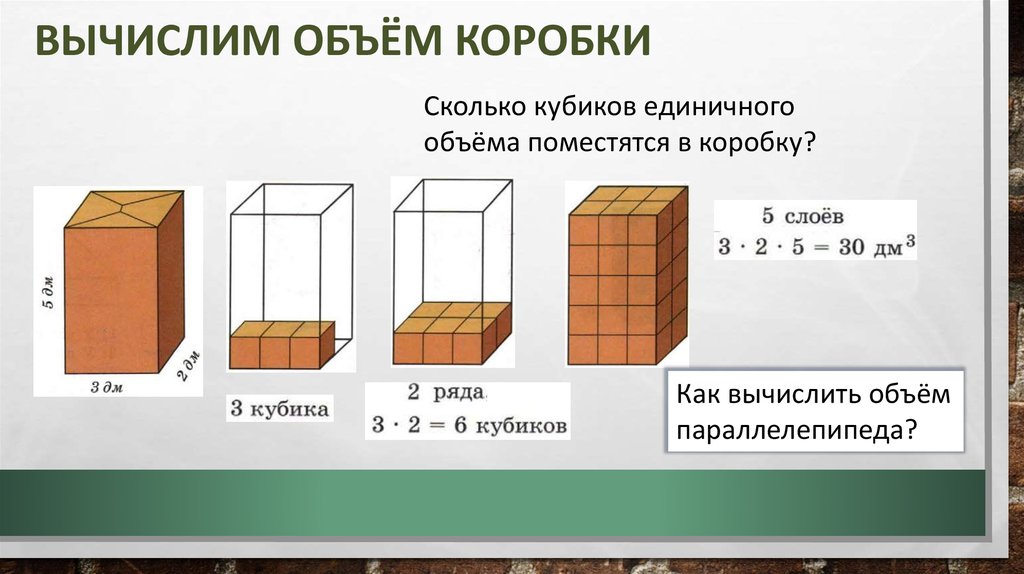 Необходимый объем уксуса можно рассчитать по приведенному ниже уравнению:

объем = 4/3 × π × 0,15 ³ = 0,141 фута ³

Конус

Конус представляет собой трехмерную форму, которая плавно сужается от своего обычно круглого основания к общей точке, называемой вершиной (или вершиной). Математически конус образован подобно кругу набором отрезков, соединенных с общей центральной точкой, за исключением того, что центральная точка не входит в плоскость, содержащую круг (или какое-либо другое основание). На этой странице рассматривается только случай конечного прямого кругового конуса. Конусы, состоящие из полулиний, некруглых оснований и т. д., которые простираются до бесконечности, рассматриваться не будут. Уравнение для расчета объема конуса выглядит следующим образом:

объем =

πr 2 ч

где r — радиус, а h — высота конуса

ПРИМЕР: Беа полна решимости выйти из магазина мороженого с хорошо потраченными 5 долларами, заработанными тяжелым трудом. Хотя она предпочитает обычные сахарные рожки, вафельные рожки, бесспорно, крупнее. Она определяет, что на 15 % предпочитает обычные сахарные рожки вафельным рожкам, и ей необходимо определить, превышает ли потенциальный объем вафельного рожка на ≥ 15 % объем сахарного рожка. Объем вафельного рожка с круглым основанием радиусом 1,5 дюйма и высотой 5 дюймов можно рассчитать с помощью приведенного ниже уравнения:

объем = 1/3 × π × 1,5 ² × 5 = 11,781 дюйма ³

Беа также вычисляет объем сахарного рожка и обнаруживает, что разница составляет < 15%, и решает купить сахарный рожок. . Теперь все, что ей нужно сделать, это использовать свою ангельскую детскую привлекательность, чтобы заставить персонал опустошить контейнеры с мороженым в ее рожок.

Куб

Куб является трехмерным аналогом квадрата и представляет собой объект, ограниченный шестью квадратными гранями, три из которых сходятся в каждой из его вершин и все перпендикулярны соответствующим соседним граням.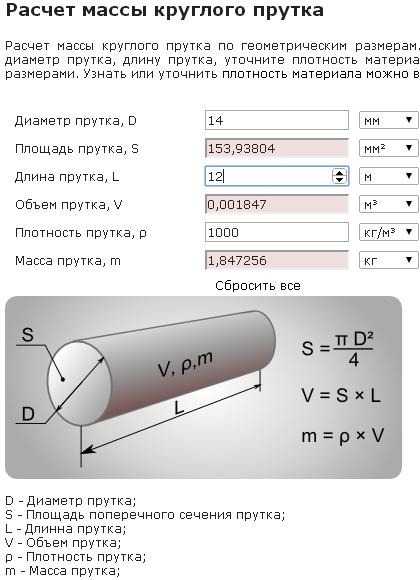 Куб является частным случаем многих классификаций фигур в геометрии, включая квадратный параллелепипед, равносторонний кубоид и правильный ромбоэдр. Ниже приведено уравнение для расчета объема куба:

объем = а ³
где a — длина ребра куба

ПРИМЕР: Боб, родившийся в Вайоминге (и никогда не покидавший штат), недавно посетил родину своих предков в Небраске. Потрясенный великолепием Небраски и окружающей средой, непохожей ни на что другое, с чем он когда-либо сталкивался ранее, Боб понял, что ему нужно привезти часть Небраски домой с собой. У Боба есть кубический чемодан с длиной ребра 2 фута, и он вычисляет объем почвы, который он может унести с собой домой, следующим образом:

объем = 2 ³ = 8 футов ³

Цилиндр

Цилиндр в его простейшей форме определяется как поверхность, образованная точками на фиксированном расстоянии от заданной прямой оси. Однако в обычном употреблении «цилиндр» относится к прямолинейному круговому цилиндру, основаниями которого являются окружности, соединенные через их центры осью, перпендикулярной плоскостям его оснований, с заданной высотой 90 253 h 90 256 и радиусом 90 253 r 90 256.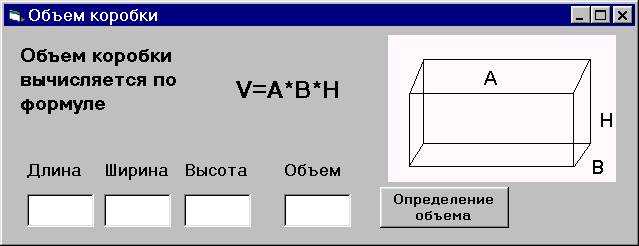 . Уравнение для расчета объема цилиндра показано ниже:

объем = πr ² ч
где r — радиус, а h — высота резервуара

ПРИМЕР: Кэлум хочет построить замок из песка в гостиной своего дома. Поскольку он решительно выступает за переработку отходов, он нашел три цилиндрические бочки с незаконной свалки и очистил их от химических отходов, используя средство для мытья посуды и воду. Каждая бочка имеет радиус 3 фута и высоту 4 фута, и Кэлум определяет объем песка, который может вместить каждая, используя приведенное ниже уравнение:

объем = π × 3 ² × 4 = 113,097 футов ³

Он успешно строит замок из песка в своем доме и, в качестве дополнительного бонуса, ему удается экономить электроэнергию на ночном освещении, так как его замок из песка светится ярко-зеленым в темноте. темнота.

Прямоугольный резервуар

Прямоугольный резервуар представляет собой обобщенную форму куба, стороны которого могут иметь различную длину. Он ограничен шестью гранями, три из которых сходятся в его вершинах и все перпендикулярны соответствующим смежным граням. Уравнение для расчета объема прямоугольника показано ниже:

объем= длина × ширина × высота

ПРИМЕР: Дарби любит торт. Она ходит в спортзал по 4 часа в день, каждый день, чтобы компенсировать свою любовь к тортам. Она планирует пройти по тропе Калалау на Кауаи, и, хотя Дарби в отличной форме, она беспокоится о своей способности пройти тропу из-за отсутствия торта. Она решает упаковать только самое необходимое и хочет наполнить свой идеально прямоугольный пакет длиной, шириной и высотой 4 фута, 3 фута и 2 фута соответственно тортом. Точный объем торта, который она может поместить в свою упаковку, рассчитывается ниже:

объем = 2 × 3 × 4 = 24 фута ³

Капсула

Капсула представляет собой трехмерную геометрическую форму, состоящую из цилиндра и двух полусферических концов, где полусфера представляет собой половину сферы. Отсюда следует, что объем капсулы можно рассчитать, комбинируя уравнения объема для сферы и прямого кругового цилиндра:

объем = πr 2 ч +

πr 3 = πr 2 (

р + ч)

где r радиус и h высота цилиндрической части

Джо может взять с собой капсулу времени, которую он хочет похоронить для будущих поколений в своем путешествии самопознания через Гималаи:

объем = π × 1,5 ² × 3 + 4/3 × π ×1,5 ³ = 35,343 футов ³

Сферическая крышка

Сферическая крышка представляет собой часть сферы, отделенную от остальной части сферы плоскостью. Если плоскость проходит через центр сферы, сферическая шапка называется полусферой. Существуют и другие различия, в том числе сферический сегмент, где сфера разделена на две параллельные плоскости и два разных радиуса, где плоскости проходят через сферу. Уравнение для расчета объема сферической шапки получено из уравнения для сферического сегмента, где второй радиус равен 0. Относительно сферической шапки, показанной в калькуляторе:

объем =

πh 2 (3R — h)

Имея два значения, предоставленный калькулятор вычисляет третье значение и объем. Уравнения для преобразования между высотой и радиусом показаны ниже:

Данный R и R : H = R ± √r ² — R ²

.0007	ч 2 + г 2
2ч

3

3

3
Даны R и h : r = √2Rh — h ²
где r — радиус основания, R — радиус сферы, а h — высота сферического колпачка

EX: Джек действительно хочет победить своего друга Джеймса в игре в гольф, чтобы произвести впечатление на Джилл, и вместо того, чтобы тренироваться, он решает саботировать мяч для гольфа Джеймса. Он отрезает идеальный сферический колпачок от верхней части мяча для гольфа Джеймса и должен рассчитать объем материала, необходимого для замены сферического колпачка и смещения веса мяча для гольфа Джеймса. Учитывая, что мяч для гольфа Джеймса имеет радиус 1,68 дюйма, а высота сферической крышки, которую срезал Джек, составляет 0,3 дюйма, объем можно рассчитать следующим образом:0003

объем = 1/3 × π × 0,3 ² (3 × 1,68 — 0,3) = 0,447 дюйма ³

К сожалению для Джека, Джеймс получил новую партию мячей за день до их игры, и все усилия Джека оказались напрасными.

Усеченный конус

Усеченный конус — это часть твердого тела, остающаяся после разрезания конуса двумя параллельными плоскостями. Этот калькулятор вычисляет объем для прямого круглого конуса специально. Типичные усеченные конусы, встречающиеся в повседневной жизни, включают абажуры, ведра и некоторые стаканы. Объем правого конического усеченного конуса рассчитывается по следующему уравнению:

объем =

πh(r 2 + rR + R 2 )

где r и R — радиусы оснований, h — высота усеченного конуса

таким образом, чтобы мороженое оставалось упакованным внутри конуса, а поверхность мороженого находилась на одном уровне и была параллельна плоскости отверстия конуса.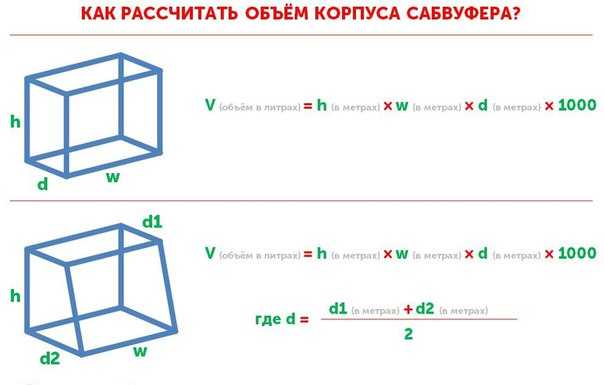 Она собирается начать есть свой рожок и оставшееся мороженое, когда ее брат хватает ее рожок и откусывает часть нижней части рожка, которая идеально параллельна ранее единственному отверстию. Беа теперь осталась с протекающим мороженым в правом коническом усеченном конусе, и ей нужно рассчитать объем мороженого, который она должна быстро съесть, учитывая высоту усеченного конуса 4 дюйма и радиусы 1,5 дюйма и 0,2 дюйма:

объем = 1/3 × π × 4 (0,2 ² + 0,2 × 1,5 + 1,5 ² ) = 10,849 в ³

поверхность, которую можно описать как деформацию сферы за счет масштабирования направленных элементов. Центром эллипсоида называется точка, в которой пересекаются три попарно перпендикулярные оси симметрии, а отрезки, ограничивающие эти оси симметрии, называются главными осями. Если все три имеют разную длину, эллипсоид обычно называют трехосным. Уравнение для расчета объема эллипсоида выглядит следующим образом:

объем =

πabc

где a , b и c длины осей мясо, поскольку он может поместиться в булочке в форме эллипса.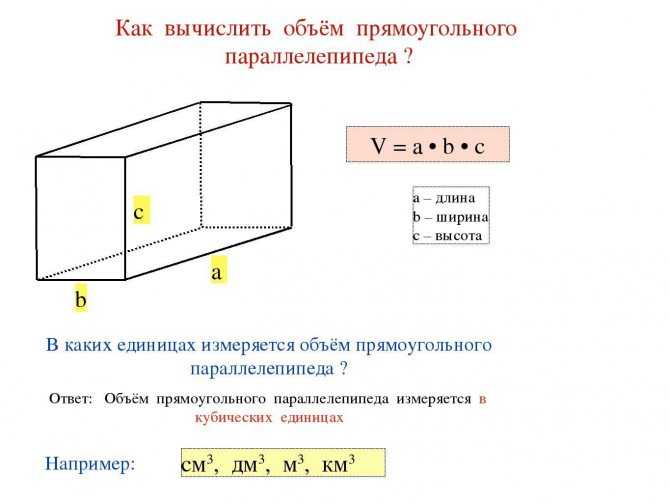 Таким образом, Хабат выдалбливает булочку, чтобы максимально увеличить объем мяса, который он может поместить в свой бутерброд. Учитывая, что осевая длина его булочки составляет 1,5 дюйма, 2 дюйма и 5 дюймов, Хабат вычисляет объем мяса, который он может поместить в каждую выдолбленную булочку, следующим образом:

объем = 4/3 × π × 1,5 × 2 × 5 = 62,832 дюйма ³

Квадратная пирамида

Пирамида в геометрии представляет собой трехмерное тело, образованное путем соединения многоугольного основания с точкой, называемой его вершиной, где многоугольник — это фигура на плоскости, ограниченная конечным числом отрезков прямой линии. Существует множество возможных многоугольных оснований для пирамиды, но квадратная пирамида — это пирамида, в которой основание — квадрат. Другое различие, связанное с пирамидами, связано с расположением вершины. Вершина правильной пирамиды находится прямо над центром тяжести ее основания. Независимо от того, где находится вершина пирамиды, если ее высота измеряется как перпендикулярное расстояние от плоскости, содержащей основание, до ее вершины, объем пирамиды можно записать как:

Обобщенный объем пирамиды:

объем =

ч/б

где b площадь основания и h высота

Объем квадратной пирамиды:

объем =

а 2 ч

где a длина края основания

ПРИМЕР: Ван очарован древним Египтом и особенно любит все, что связано с пирамидами.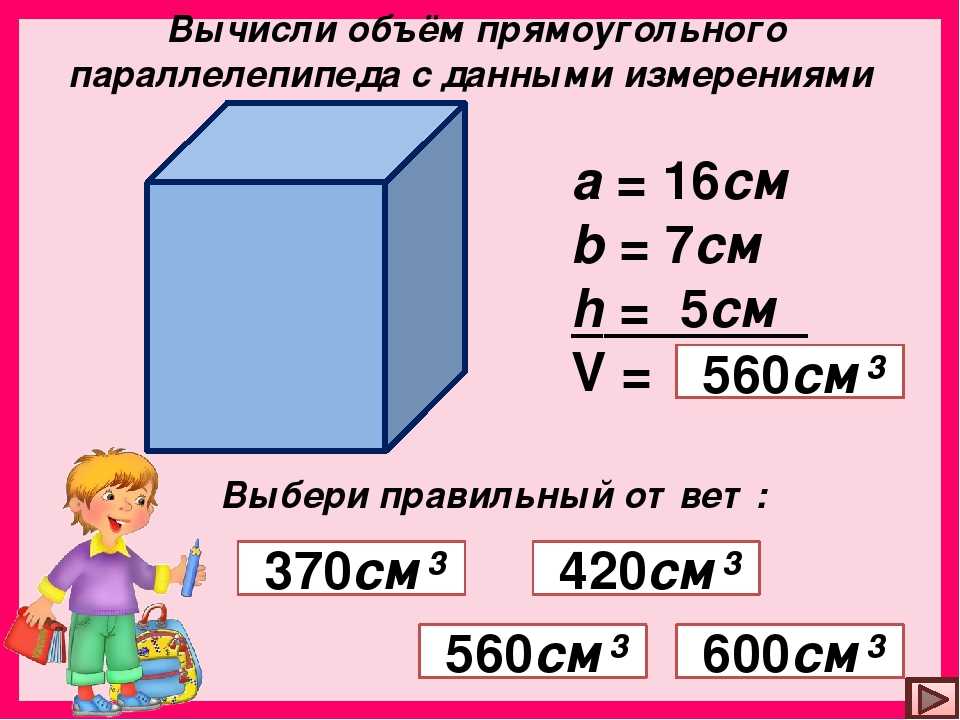 Будучи старшим из своих братьев и сестер Ту, Три и Форе, он может легко загнать их в загон и использовать по своему желанию. Воспользовавшись этим, Ван решает воспроизвести древние египетские времена и попросить своих братьев и сестер выступить в роли рабочих, строящих ему пирамиду из грязи с длиной ребра 5 футов и высотой 12 футов, объем которой можно рассчитать с помощью уравнения для квадрата. пирамида:

объем = 1/3 × 5 ² × 12 = 100 футов ³

Трубчатая пирамида

Трубка, часто также называемая трубой, представляет собой полый цилиндр, который часто используется для передачи жидкостей или газов. . Вычисление объема трубы по существу использует ту же формулу, что и для цилиндра ( объем = pr ² h ), за исключением того, что в этом случае используется диаметр, а не радиус, и длина используется, а не высота. Таким образом, формула включает измерение диаметров внутреннего и внешнего цилиндров, как показано на рисунке выше, вычисление каждого из их объемов и вычитание объема внутреннего цилиндра из объема внешнего.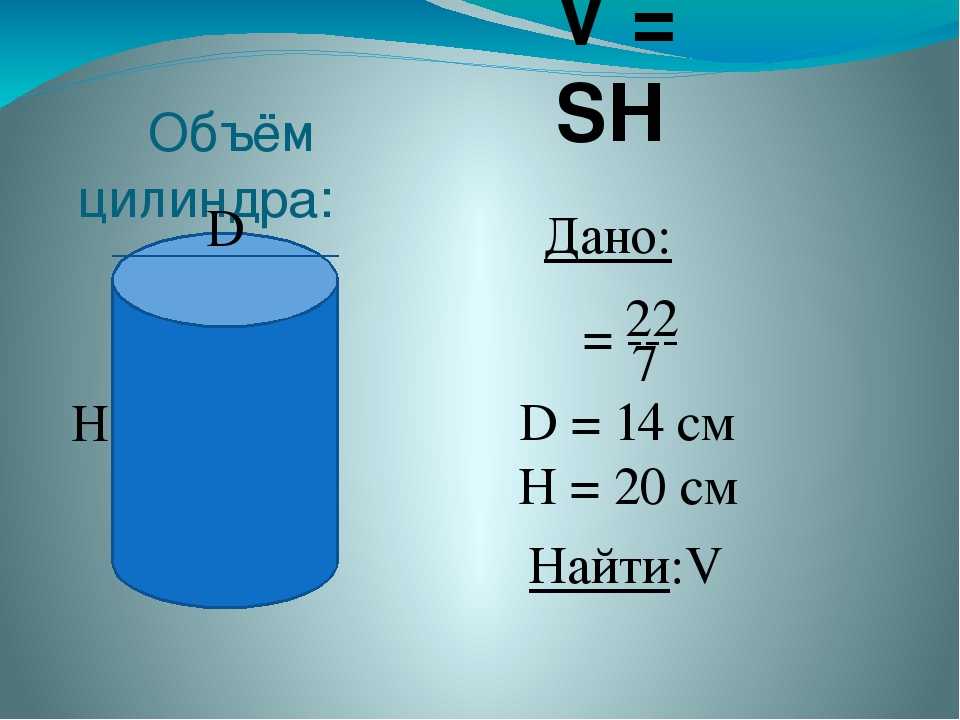 С учетом использования длины и диаметра, упомянутых выше, формула для расчета объема трубы показана ниже:

объем = π	D 1 2 — D 2 2 4
4

.

л

, где d ₁ — внешний диаметр, d ₂ — внутренний диаметр, а l — длина трубы. Ее строительная компания использует только самые экологически чистые материалы. Она также гордится тем, что удовлетворяет потребности клиентов. У одного из ее клиентов есть загородный дом, построенный в лесу, через ручей. Он хочет более легкого доступа к своему дому и просит Беулу построить ему дорогу, обеспечив при этом свободное течение ручья, чтобы не мешать его любимому месту рыбалки. Она решает, что надоедливые бобровые плотины были бы хорошей точкой для прокладки трубы через ручей. Объем запатентованного ударопрочного бетона, необходимый для строительства трубы с внешним диаметром 3 фута, внутренним диаметром 2,5 фута и длиной 10 футов, можно рассчитать следующим образом:

объем = π ×

3 2 — 2,5 2 4

× l0 = 21,6 фута 3

Общие единицы объема

Калькулятор объема 📐 — Рассчитайте объем куба, коробки, цилиндра, сферы, конуса…

    Быстрая навигация:

1. Как рассчитать объем тела?
2. Объем куба
3. Объем коробки
4. Объем цилиндра
5. Объем сферы
6. Объем конуса
7. Объем треугольной призмы
8. Примеры применения формул объема

    Как рассчитать объем тела?

В зависимости от конкретного тела существуют разные формулы и разная необходимая информация для расчета его объема.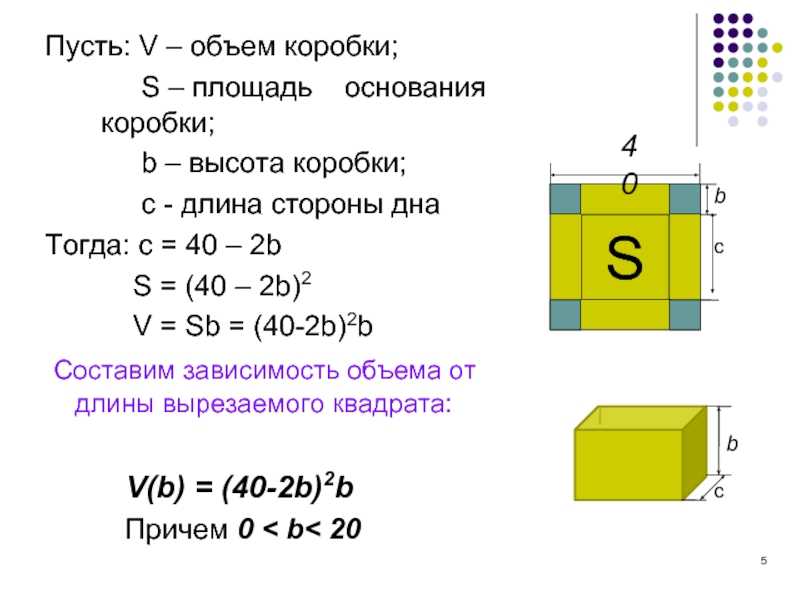 Ниже приведены формулы объема для наиболее распространенных типов геометрических тел — все они поддерживаются нашим онлайн-калькулятором объема выше. Все меры должны быть в одних и тех же единицах. Результат всегда в кубических единицах: кубические сантиметры, кубические дюймы, кубические метры, кубические футы, кубические ярды и т. д.

Вычисления объема полезны во многих науках, в строительных работах и ​​планировании, в грузовых перевозках, в контроле климата (например, расчеты кондиционирования воздуха), управлении плавательными бассейнами и многом другом.

    Объем куба

Формула объема куба: сторона ³ , как показано на рисунке ниже:

нашли объем куба. Это то же самое, что умножить площадь поверхности одной стороны на глубину куба. Для этого типа цифр едва ли нужен калькулятор, чтобы сделать математику.

    Объем коробки

Чтобы найти объем прямоугольной коробки, используйте формулу высота x ширина x длина , как показано на рисунке ниже:

Чтобы вычислить объем коробки или прямоугольника баку нужны три измерения: ширина, длина и высота. Их обычно легко измерить из-за регулярности формы. Обозначив одно измерение как глубину или высоту прямоугольной призмы, умножение двух других дает нам площадь поверхности, которую затем необходимо умножить на глубину / высоту, чтобы получить объем. Чтобы рассчитать объем бака другой формы, воспользуйтесь нашим калькулятором объема бака.

    Объем цилиндра

Формула объема цилиндра: высота x π x (диаметр / 2) ² , где (диаметр / 2) — радиус основания (d = 2 x r) , так что другой способ записать это: высота x π x радиус ² . Наглядно на рисунке ниже:

Вам нужны два измерения: высота цилиндра и диаметр его основания. Во многих школьных формулах вместо этого дается радиус, но в реальных ситуациях гораздо проще измерить диаметр, чем пытаться точно определить середину круглого основания, чтобы вы могли измерить радиус. Наш калькулятор объема требует, чтобы вы ввели диаметр основания. Через диаметр можно рассчитать площадь поверхности основания, а затем, чтобы получить объем, просто умножить его на высоту цилиндра.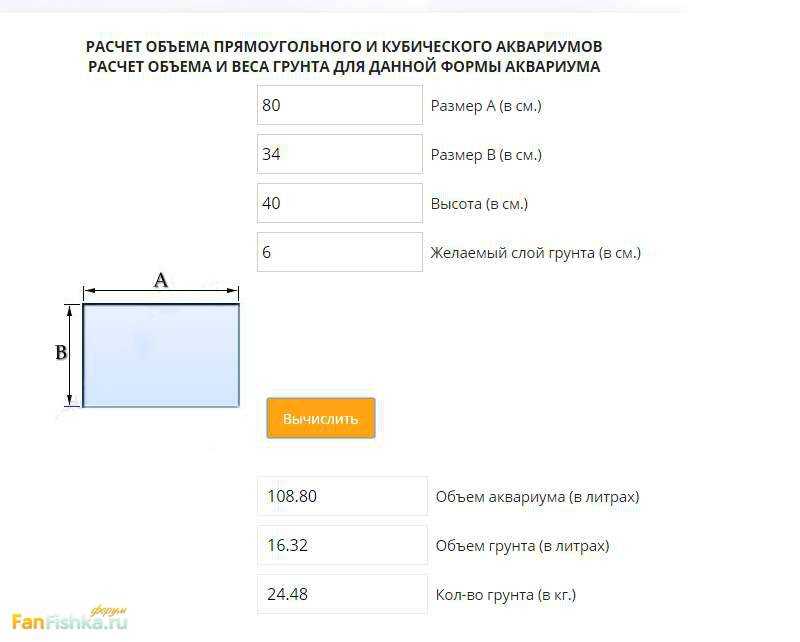

    Объем сферы

Чтобы найти объем сферы, используйте формулу 4/3 x π x (диаметр / 2) ³ , где (диаметр / 2) — радиус сфера (d = 2 x r), так что другой способ записать это 4/3 x π x радиус ³ . Визуально на рисунке ниже:

То же, что и круг, вам нужно только одно измерение сферы: диаметр или радиус.

    Объем конуса

Формула объема конуса: (высота x π x (диаметр / 2) ² ) / 3 , где (диаметр / 2) — радиус основания (d = 2 x r), поэтому по-другому чтобы написать это (высота x π x радиус ² ) / 3 , как показано на рисунке ниже:

обычный конус. Для конусов неправильной формы, которые еще не поддерживаются нашим инструментом, вам также необходимо знать угол конуса.

    Объем треугольной призмы

Формула объема треугольной призмы: (высота x основание x длина) / 2 , как показано на рисунке ниже:

Аналогично прямоугольным коробкам всего три измерения: высота, основание и длина, чтобы найти его объем.