Принцип наименьшего действия. Часть 1 / Хабр

Когда я впервые узнал об этом принципе, у меня возникло ощущение какой-то мистики. Такое впечатление, что природа таинственным образом перебирает все возможные пути движения системы и выбирает из них самый лучший.

Сегодня я хочу немного рассказать об одном из самых замечательных физических принципов – принципе наименьшего действия.

Предыстория

Со времен Галилея было известно, что тела, на которые не действуют никакие силы, двигаются по прямым линиям, то есть по кратчайшему пути. По прямым линиям распространяются и световые лучи.

При отражении свет также двигается таким образом, чтобы добраться из одной точки в другую кратчайшим путем. На картинке кратчайшим будет зеленый путь, при котором угол падения равен углу отражения. Любой другой путь, например, красный, окажется длиннее.

Это несложно доказать, просто отразив пути лучей на противоположную сторону от зеркала. На картинке они показаны пунктиром.

Видно, что зеленый путь ACB превращается в прямую ACB’. А красный путь превращается в изломанную линию ADB’, которая, конечно длиннее зеленой.

В 1662 Пьер Ферма предположил, что скорость света в плотном веществе, например, в стекле, меньше, чем в воздухе. До этого общепринятой была версия Декарта, согласно которой скорость света в веществе должна быть больше, чем в воздухе, чтобы получался правильный закон преломления. Для Ферма предположение, что свет может двигаться в более плотной среде быстрее, чем в разреженной казалось противоестественным. Поэтому он предположил, что все в точности наоборот и доказал удивительную вещь – при таком предположении свет преломляется так, чтобы достичь место назначения за минимальное время.

На рисунке опять, зеленым цветом показан путь, по которому в действительности двигается световой луч. Путь, отмеченный красным цветом, является кратчайшим, но не самым быстрым, потому что свету приходится больший путь проходить в стекле, а в нем его скорость меньше. Самым быстрым является именно реальный путь прохождения светового луча.

Все эти факты наводили на мысль, что природа действует каким-то рациональным образом, свет и тела двигаются наиболее оптимально, затрачивая как можно меньше усилий. Но что это за усилия, и как их посчитать оставалось загадкой.

В 1744 Мопертюи вводит понятие «действия» и формулирует принцип, согласно которому истинная траектория частицы отличается от любой другой тем, что действие для неё является минимальным. Однако сам Мопертюи, так и не смог дать четкого определения чему равно это действие. Строгая математическая формулировка принципа наименьшего действия была разработана уже другими математиками – Эйлером, Лагранжем, и окончательно была дана Уильямом Гамильтоном:

На математическом языке принцип наименьшего действия формулируется достаточно кратко, однако не для всех читателей может быть понятен смысл используемых обозначений. Я хочу попытаться объяснить этот принцип более наглядно и простыми словами.

Свободное тело

Итак, представьте, что вы сидите в машине в точке и в момент времени вам дана простая задача: к моменту времени вам нужно доехать на машине до точки .

Топливо для машины дорого стоит и, конечно, вам хочется потратить его как можно меньше. Машина у вас сделана по новейшим супер-технологиям и может разгоняться или тормозить как угодно быстро. Однако, устроена она так, что чем быстрее она едет, тем больше потребляет топлива. Причем потребление топлива пропорционально квадрату скорости. Если вы едете в два раза быстрее, то за тот же промежуток времени потребляете в 4 раза больше топлива. Кроме скорости, на потребление топлива, конечно же влияет и масса автомобиля. Чем тяжелее наш автомобиль, тем больше топлива он потребляет. У нашего автомобиля потребление топлива в каждый момент времени равно , т.е. в точности равно кинетической энергии автомобиля.

Так как же нужно ехать, чтобы добраться к пункту к точно назначенному времени и израсходовать топлива как можно меньше? Ясно, что ехать нужно по прямой. При увеличении проезжаемого расстояния топлива израсходуется точно не меньше. А дальше можно избрать разные тактики. Например, можно быстро приехать в пункт заранее и просто посидеть, подождать, когда наступит время . Скорость езды, а значит и потребление топлива в каждый момент времени при этом получится большой, но ведь и время езды сократится. Возможно, общий расход топлива при этом будет не так уж и велик. Или можно ехать равномерно, с одной и той же скоростью, такой, чтобы, не торопясь, точно приехать в момент времени . Или часть пути проехать быстро, а часть медленнее. Как же лучше ехать?

Оказывается, что самый оптимальный, самый экономный способ езды – это ехать с постоянной скоростью, такой, чтобы оказаться в пункте в точно назначенное время . При любом другом варианте топлива израсходуется больше. Можете сами проверить на нескольких примерах. Причина в том, что потребление топлива возрастает пропорционально квадрату скорости. Поэтому при увеличении скорости потребление топлива возрастает быстрее, чем сокращается время езды, и общий расход топлива также возрастает.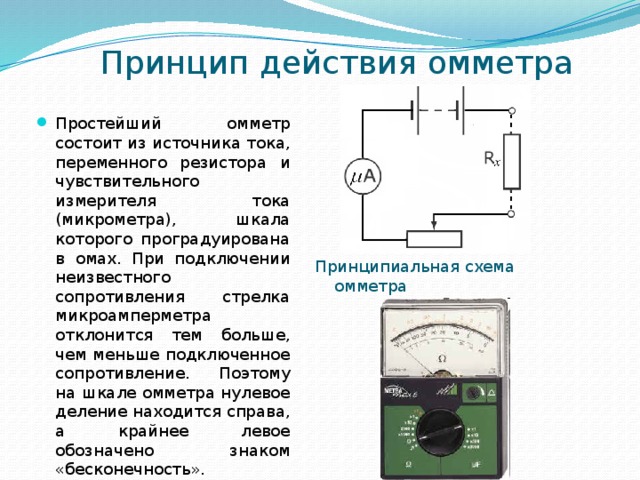

Итак, мы выяснили, что если автомобиль в каждый момент времени потребляет топливо пропорционально своей кинетической энергии, то самый экономный способ добраться из точки в точку к точно назначенному времени – это ехать равномерно и прямолинейно, точно так, как двигается тело в отсутствие действующих на него сил. Любой другой способ движения приведет к большему общему расходу топлива.

В поле тяжести

Теперь давайте немного усовершенствуем наш автомобиль. Давайте приделаем к нему реактивные двигатели, чтобы он мог свободно летать в любом направлении. В целом конструкция осталась той же, поэтому расход топлива опять остался строго пропорционален кинетической энергии автомобиля. Если теперь дано задание вылететь из точки в момент времени и прилететь в точку к моменту времени , то наиболее экономичный способ, как и прежде, конечно, будет лететь равномерно и прямолинейно, чтобы оказаться в точке в точно назначенное время . Это опять соответствует свободному движению тела в трехмерном пространстве.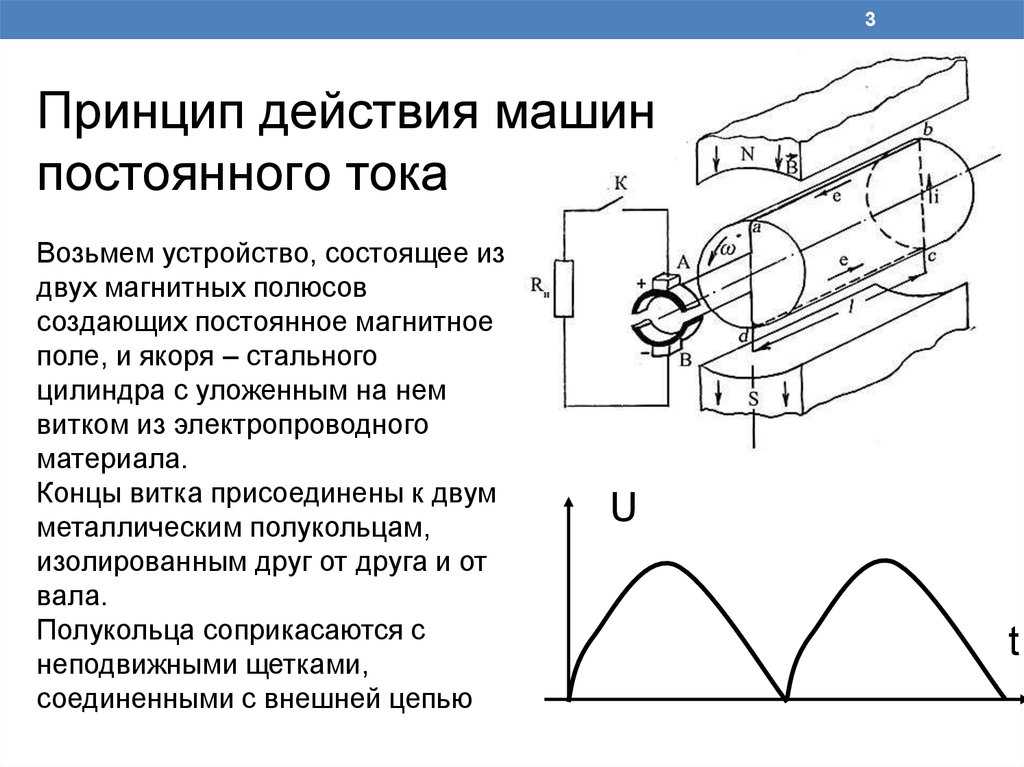

Однако, в последнюю модель автомобиля установили необычный аппарат. Данный аппарат умеет вырабатывать топливо буквально из ничего. Но конструкция такова, что чем выше находится автомобиль, тем больше топлива в каждый момент времени вырабатывает аппарат. Выработка топлива прямо пропорциональна высоте , на которой в данный момент находится автомобиль. Также, чем тяжелее автомобиль, тем более мощный аппарат на нем установлен и тем больше топлива он вырабатывает, и выработка прямо пропорциональна массе автомобиля . Аппарат получился таким, что выработка топлива точно равна (где – ускорение свободного падения), т.е. потенциальной энергии автомобиля.

Потребление топлива в каждый момент времени получается равным кинетической энергии минус потенциальной энергии автомобиля (минус потенциальной энергии, потому что установленный аппарат вырабатывает топливо, а не тратит). Теперь наша задача наиболее экономного движения автомобиля между пунктами и становится сложнее. Прямолинейное равномерное движение оказывается в данном случае не самым эффективным. Оказывается, более оптимально — немного набрать высоты, какое-то время там задержаться, выработав побольше топлива, а затем уже спуститься в точку . При правильной траектории полета общая выработка топлива за счет набора высоты перекроет дополнительные расходы топлива на увеличение длины пути и увеличения скорости. Если аккуратно посчитать, то самым экономным способом для автомобиля будет лететь по параболе, точно по такой траектории и с точно такой скоростью, с какой летел бы камень в поле тяжести Земли.

Здесь стоит сделать разъяснение. Конечно, можно из точки кинуть камень многими разными способами так, чтобы он попал в точку . Но кидать его нужно так, чтобы он, вылетев из точки в момент времени , попал в точку точно в момент времени . Именно это движение будет самым экономным для нашего автомобиля.

Функция Лагранжа и принцип наименьшего действия

Теперь мы можем перенести эту аналогию на реальные физические тела. Аналог интенсивности потребления топлива для тел называют функцией Лагранжа или Лагранжианом (в честь Лагранжа) и обозначают буквой . Лагранжиан показывает насколько много «топлива» потребляет тело в данный момент времени. Для тела, движущегося в потенциальном поле, Лагранжиан равен его кинетической энергии минус потенциальной энергии.

Аналог общего количества израсходованного топлива за все время движения, т.е. значение Лагранжиана, накопленное за все время движения, называется «действием».

Принцип наименьшего действия состоит в том, что тело двигается таким образом, чтобы действие (которое зависит от траектории движения) было минимальным. При этом не нужно забывать, что заданы начальное и конечное условия, т.е. где тело находится в момент времени и в момент времени .

При этом тело не обязательно должно двигаться в однородном поле тяготения, которое мы рассматривали для нашего автомобиля. Можно рассматривать совершенно другие ситуации. Тело может колебаться на резинке, качаться на маятнике или летать вокруг Солнца, во всех этих случаях оно движется так, чтобы минимизировать «общий расход топлива» т. е. действие.

Если система состоит из нескольких тел, то Лагранжиан такой системы будет равен суммарной кинетической энергии всех тел минус суммарной потенциальной энергии всех тел. И опять, все тела будут согласованно двигаться так, чтобы действие всей системы при таком движении было минимальным.

Не все так просто

На самом деле я немного обманул, сказав, что тела всегда двигаются так, чтобы минимизировать действие. Хотя в очень многих случаях это действительно так, можно придумать ситуации, в которых действие явно не минимально.

Например, возьмем шарик и поместим его в пустое пространство. На некотором отдалении от него поставим упругую стенку. Допустим, мы хотим, чтобы через некоторое время шарик оказался в том же самом месте. При таких заданных условиях шарик может двигаться двумя разными способами. Во-первых, он может просто оставаться на месте. Во-вторых, можно его толкнуть по направлению к стенке. Шарик долетит до стенки, отскочит от нее и вернется обратно. Понятно, что можно толкнуть его с такой скоростью, чтобы он вернулся в точно нужное время.

Оба варианта движения шарика возможны, но действие во втором случае получится больше, потому что все это время шарик будет двигаться с ненулевой кинетической энергией.

Как же спасти принцип наименьшего действия, чтобы он был справедлив и в таких ситуациях? Об этом мы поговорим в следующий раз.

Принцип наименьшего действия в аналитической механике / Хабр

Причина данной публикации — неоднозначная статья на тему принципа наименьшего действия (ПНД), опубликованная на ресурсе несколько дней назад. Неоднозначна она потому, что её автор в популярной форме пытается донести до читателя один из основополагающих принципов математического описания природы, и это частично ему удается. Если бы не одно но, притаившееся в конце публикации. Под спойлером приведена полная цитата данного отрывка

Задача о движении шарика

На самом деле я немного обманул, сказав, что тела всегда двигаются так, чтобы минимизировать действие. Хотя в очень многих случаях это действительно так, можно придумать ситуации, в которых действие явно не минимально.

Например, возьмем шарик и поместим его в пустое пространство. На некотором отдалении от него поставим упругую стенку. Допустим, мы хотим, чтобы через некоторое время шарик оказался в том же самом месте. При таких заданных условиях шарик может двигаться двумя разными способами. Во-первых, он может просто оставаться на месте. Во-вторых, можно его толкнуть по направлению к стенке. Шарик долетит до стенки, отскочит от нее и вернется обратно. Понятно, что можно толкнуть его с такой скоростью, чтобы он вернулся в точно нужное время.

Оба варианта движения шарика возможны, но действие во втором случае получится больше, потому что все это время шарик будет двигаться с ненулевой кинетической энергией.

Как же спасти принцип наименьшего действия, чтобы он был справедлив и в таких ситуациях? Об этом мы поговорим в следующий раз.

Так в чем же, с моей точки зрения, проблема?

Проблема в том, что автор, приводя данный пример допустил ряд фундаментальных ошибок. Она усугубляется тем, что планируемая вторая часть, со слов автора, будет опираться на эти ошибки. Руководствуясь принципом наполнения ресурса достоверной информацией я вынужден выступить с разъяснением своей позиции по данному вопросу более развернуто, и формат комментариев для этого маловат.

Данная статья расскажет о том, как строится механика на базе ПНД, и постарается объяснить читателю, что проблема, которую ставит автор цитируемой публикации отсутствует.

Действием по Гамильтону называют функционал

где

— функция Лагранжа, для некоторой механической системы, в которой (опуская аргументы в дальнейшем) T — кинетическая энергия системы; П — потенциальная её энергия; q(t) — вектор обобщенных координат этой системы, являющийся функцией времени. при этом полагают, что моменты времени t₁ и t₂ — фиксированы.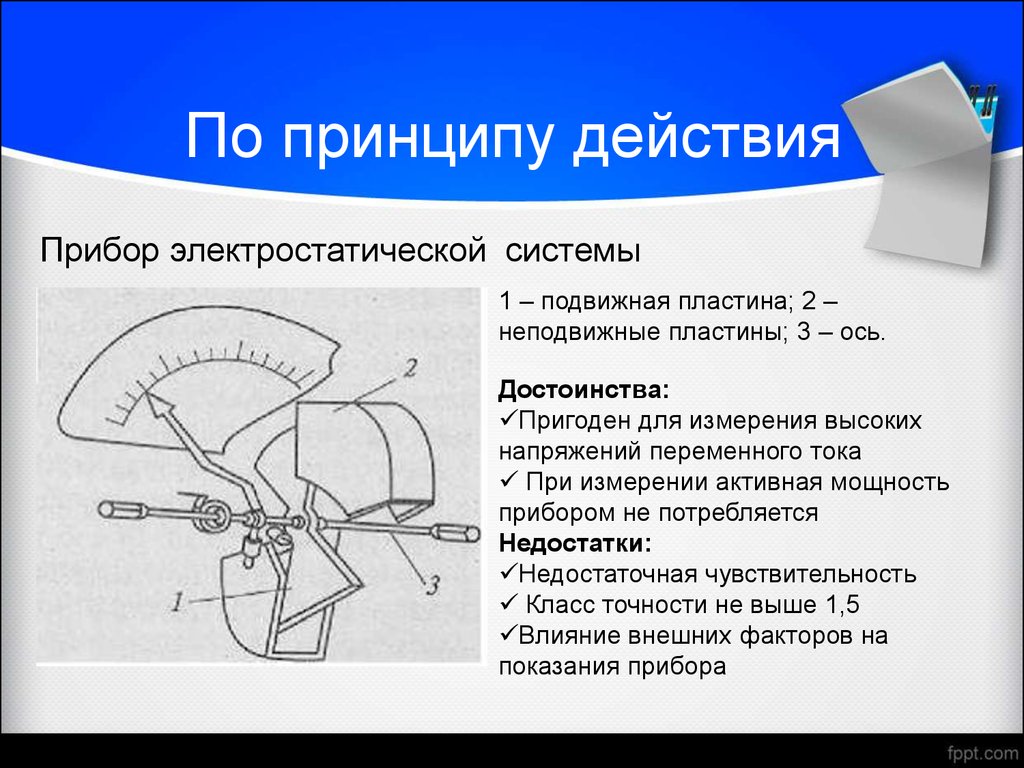

Почему функционал, а не функция? Потому, что функция, по определению есть правило, по которому одному числу из области определения (аргументу функции) ставится в соответствие другое число из области значений. Функционал отличается тем, что качестве его аргумента выступает не число, а целая функция. В данном случае это закон движения механической системы q(t), определенный по крайней мере на промежутке времени между t₁ и t₂.

Многолетние (и это мягко сказано!) труды ученых-механиков (включая умопомрачительного Леонарда Эйлера), позволили сформулировать

Принцип наименьшего действия:

Механическая система, для которой задана функция Лагранжа , движется таким образом, что закон её движения q(t) доставляет минимум функционалу

называемому действием по Гамильтону.

Уже из самого определения ПНД следует тот факт, что данный принцип приводит к уравнениям движения лишь для ограниченного класса механических систем. Для каких? А давайте разберемся.

Как следует из определения, опять таки, функции Лагранжа, ПНД позволяет получить уравнения движения для механических систем, силовое воздействие на которые определяется исключительно потенциальной энергией. Для того чтобы разобраться, о каких системах идет речь, дадим несколько определений, которые, для экономии объема статьи я помещаю под спойлер

Работа силы на перемещении

Рассмотрим движущуюся по траектории AB точку, к которой приложена сила . Бесконечно малое перемещение точки по траектории определяется вектором , направленным по касательной к траектории.

Элементарной работой силы на перемещении называют скалярную величину, равную

Тогда, полная работа силы на перемещении точки по траектории AB есть криволинейный интеграл

Кинетическая энергия точки

Кинетической энергией точки T называют работу, которую должны совершить приложенные к точке массой m силы, для того чтобы из состояния покоя перевести точку в движение со скоростью

Вычислим кинетическую энергию, согласно данному определению.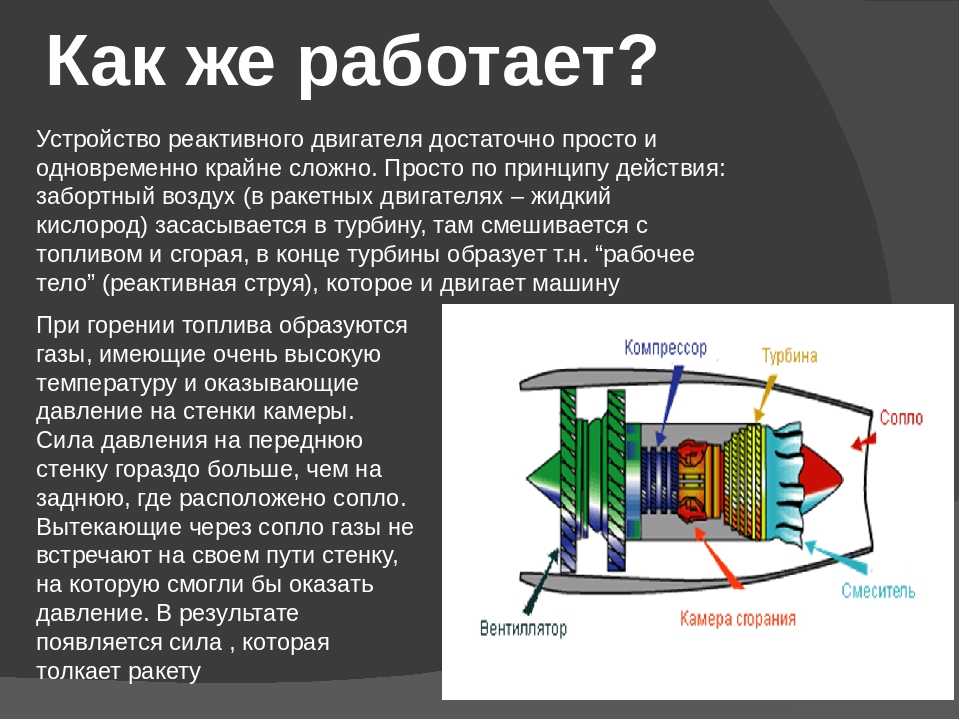 Пусть точка начинает движение из состояния покоя под действием приложенных к ней сил. На отрезке траектории AB она приобретает скорость . Вычислим работу, совершенную приложенными к точке силами, которые, по принципу независимости действия сил, заменим равнодействующей

В соответствии со вторым законом Ньютона

тогда

Вычислим строго стоящее под знаком интеграла скалярное произведение, для чего продифференцируем по времени скалярное произведение вектора скорости самого на себя

С другой стороны,

Дифференцируя это равенство по времени, имеем

Сравнивая (1) и (2) приходим к выводу, что

Тогда, спокойно вычисляем работу, раскрывая криволинейный интеграл через определенный, взяв в качестве пределов модуль скорости точки в начале и в конце траектории

Консервативные силы и потенциальная энергия точки

Рассмотрим действующую на точку силу, причем такую, что величина и направление этой силы зависит исключительно от положения точки в пространстве

Пусть точка перемещается в пространстве по произвольной траектории AB. Вычислим, какую работу при этом совершит сила (3)

Так как проекции силы на оси координат зависят исключительно от этих самых координат, всегда можно найти функцию

такую, что

Тогда, выражение для работы преобразуется к виду

где — значения функции U(x, y, z) в точках A и B соответственно. Таким образом работа рассматриваемой нами силы не зависит от траектории точки, а определяется только значениями функции U в начале и в конце траектории. Такая сила называется консервативной силой, а соответствующая ей функция U(x, y, z) — силовой функцией. Очевидно, что , а так же равенство нулю работы консервативной силы при движении по замкнутой траектории. Говорят так же, что функция U(x, y, z) задает в пространстве силовое поле.

Потенциальной энергией точки, в пространстве с заданным силовым полем, называют работу внешних сил, приложенных к ней, которую они совершают при перемещении точки в заданное координатами (x, y, z) положение в пространстве из некоторого произвольного положения, выбранного в качестве начала отсчета уровня потенциальной энергии.

Выберем на рассмотренной ранее траектории точки произвольную точку O, лежащую между точками A и B. Положим, что в точке О потенциальная энергия равна нулю. Тогда, согласно определению

— потенциальная энергия точки в положении A, а

— потенциальная энергия точки в положении B. Учитывая всё вышесказанное снова вычислим работу потенциальных сил на перемещении из точки A в точку B

Таким образом, работа консервативных сил равна изменению потенциальной энергии точки, взятому с обратным знаком

причем выбор уровня, на котором мы считаем потенциальную энергию равной нулю совершенно не влияет на результат. Отсюда можно сделать вывод, что уровень отсчета потенциальной энергии можно выбрать совершенно произвольно.

Итак, рассмотрим теперь механическую систему, движущуюся под действием потенциальных сил, положение которой однозначно задается вектором обобщенных координат

где s — число степеней свободы данной системы.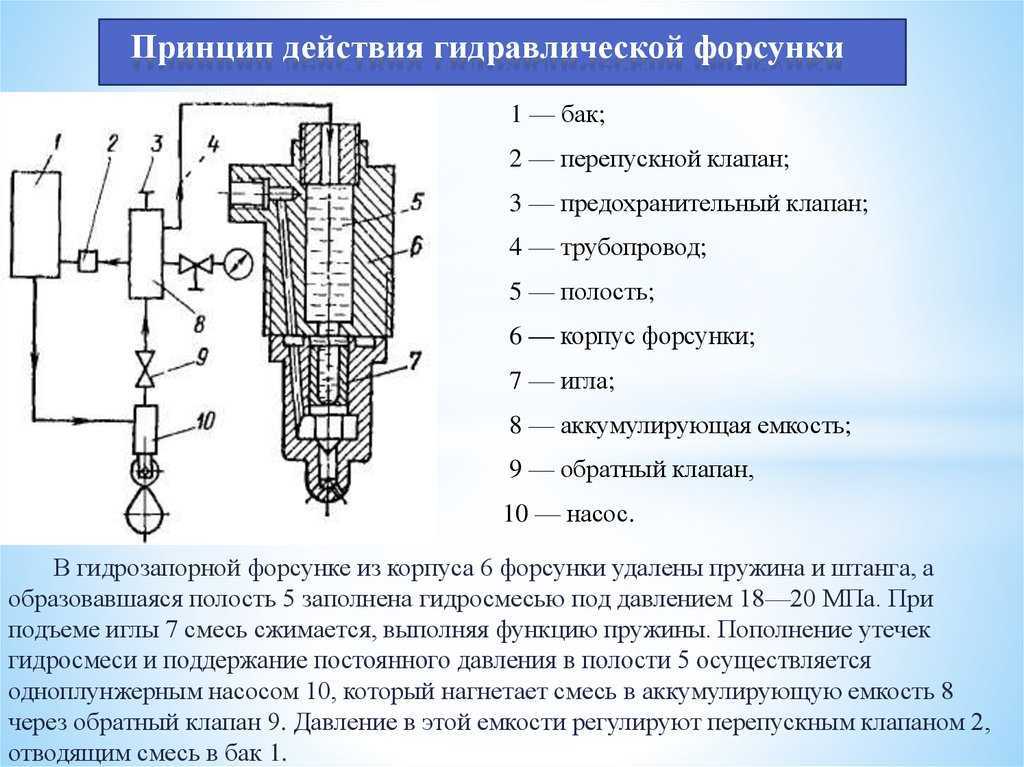

Действительный, но неизвестный пока нам, закон движения данной системы определяется зависимость обобщенных координат (4) от времени. Рассмотрим одну из обобщенных координат , полагая аналогичные рассуждения и для всех остальных координат.

Рисунок 1. Действительное и окольное движение механической системы

На рисунке зависимость изображена красной кривой. Выберем два произвольных фиксированных момента времени t₁ и t₂, полагая t₂ > t₁. Положение системы договоримся называть начальным положением системы, а — конечным положением системы.

Однако, я ещё раз настаиваю на том, чтобы нижеследующий текст был прочтен внимательно! Несмотря на то, что мы задаемся начальным и конечным положением системы, ни первое положение, ни второе, нам заранее неизвестны! Равно как и неизвестен закон движения системы! Эти положения рассматриваются именно как начальное и конечное положение, безотносительно конкретных значений.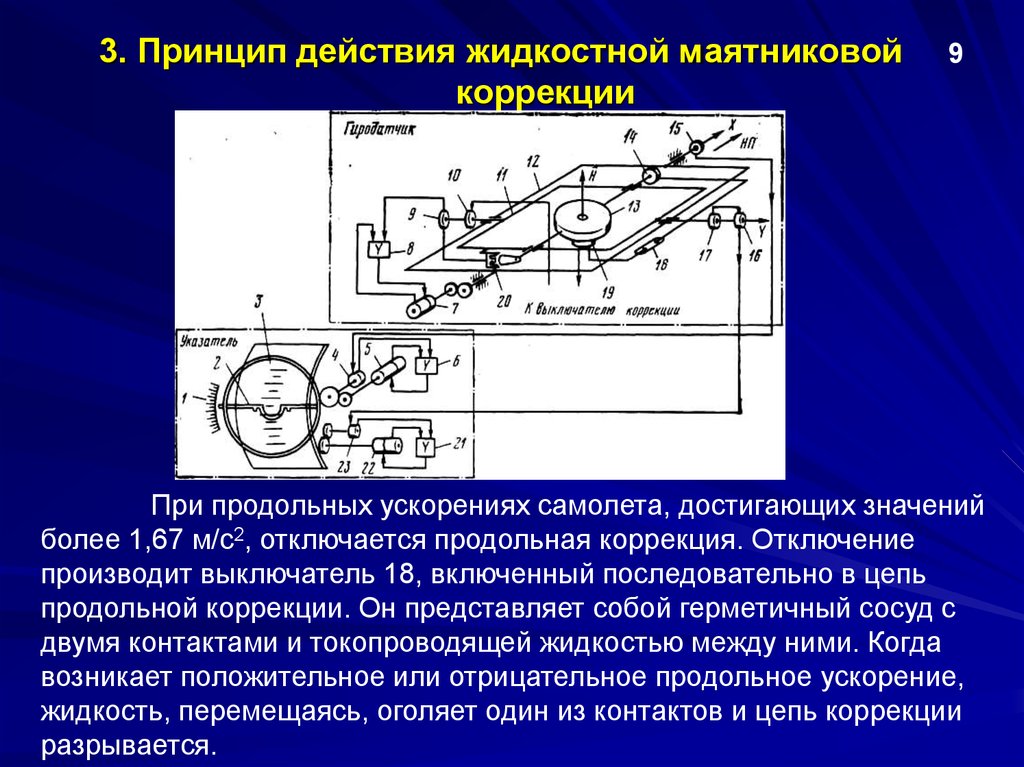

Далее мы полагаем, что из начального положения в конечное система может придти разными путями, то есть зависимость может быть любой кинематически возможной. Действительное движение системы будет существовать в единственном варианте (красная кривая), остальные кинематически возможные варианты будем называть окольными движениями (синяя кривая на рисунке). Разность между действительным и окольным движением

будем называть изохронными вариациями обобщенных координат

В данном контексте вариации (5) следует понимать как бесконечно малые функции, выражающие отклонение окольного движения от действительного. Малая «дельта» для обозначения выбрана не случайно и подчеркивает принципиальное отличие вариации от дифференциала функции. Дифференциал — главная линейная часть приращения функции, вызванного приращением аргумента. В случае с вариацией изменение значения функции при постоянном значении аргумента вызвано изменением вида самой функции! Мы не варьируем аргумент, в роли которого выступает время, поэтому вариация называется изохронной. Мы варьируем правило по которому каждому значению времени приводится в соответствие некоторое значение обобщенных координат!

По сути, мы варьируем закон движения, по которому система из начального состояния перемещается в конечное состояние. Начальное и конечное состояние определяются действительным законом движения, но я ещё раз подчеркиваю — их конкретные значения нам не известны и могут быть любыми кинематически возможными, мы лишь полагаем, что они существуют и система гарантированно перемещается из одного положения в другое! В начальном и конечном положении системы мы не варьируем закон движения, поэтому вариации обобщенных координат в начальном и конечном положении равны нулю

Исходя из принципа наименьшего действия, действительное движение системы должно быть таким, чтобы доставлять минимум функционалу действия. Варьирование координат вызывает изменение функционала действия. Необходимым условием достижения функционалом действия экстремального значения является равенство нулю его вариации

Решим поставленную нами вариационную задачу, для чего вычислим полную вариацию функционала действия и приравняем её к нулю

Загоним всё под один интеграл, и так как для вариаций справедливы все операции над бесконечно малыми величинами, преобразуем этот крокодил к виду

Исходя из определения обобщенной скорости

Тогда выражение (8) преобразуется к виду

Второе слагаемое интегрируется по частям

Исходя из условия (7), имеем

тогда, получаем уравнение

При произвольных пределах интегрирования равенство нулю определенного интеграла обеспечивается равенством нулю подынтегральной функции

С учетом того, что вариации обобщенных координат независимы, (11) справедливо только в случае равенства нулю всех коэффициентов при вариациях, то есть

Никто не мешает нам умножить каждое из уравнений на (-1) и получить более привычную запись

Уравнения (12) и есть решение задачи. И вот на этом моменте ещё раз внимание — решение вариационной задачи по принципу наименьшего действия, это не функция, доставляющая минимум действию по Гамильтону, а система дифференциальных уравнений, решая которое таковую функцию можно найти. В данном случае это дифференциальное уравнение Лагранжа 2-го рода, записанное через функцию Лагранжа, то есть в формулировке для консервативных механических систем.

И всё, на этом принцип наименьшего действия заканчивается, а начинается теория обыкновенных дифференциальных уравнений, которая, в частности, гласит, что решением уравнения (12) является вектор-функция вида

где C₁,…,C_2s — произвольные константы интегрирования.

Таким образом

ПНД — фундаментальный принцип, позволяющий получить уравнения движения системы, для которой определена функция Лагранжа

Точка! В задачах аналитической механики вышеперечисленные выкладки больше не нужно проделывать, достаточно использовать их результат (12). Функция, удовлетворяющая уравнению (12) есть закон движения системы, удовлетворяющей ПНД.

Теперь вернемся к той задаче, с которой всё началось — об одномерном движении шарика около абсолютно упругой стенки. Разумеется, для данной задачи можно получить дифференциальные уравнения движения. Так как это дифференциальные уравнения движения, то любое, я подчеркиваю это, любое их решение доставляет минимум функционалу действия, а значит ПНД выполняется! Общее решение уравнений движения шарика можно изобразить в виде так называемого фазового портрета рассматриваемой механической системы. Вот этот фазовый портрет

Рисунок 2. Фазовый портрет системы в задаче с шариком

По горизонтальной оси откладывается координата шарика, по вертикальной — проекция скорости на ось x. Может это покажется странным, но данный чертеж отражает все возможные фазовые траектории движения шарика, при любых начальных, или если вам так хочется, краевых условиях.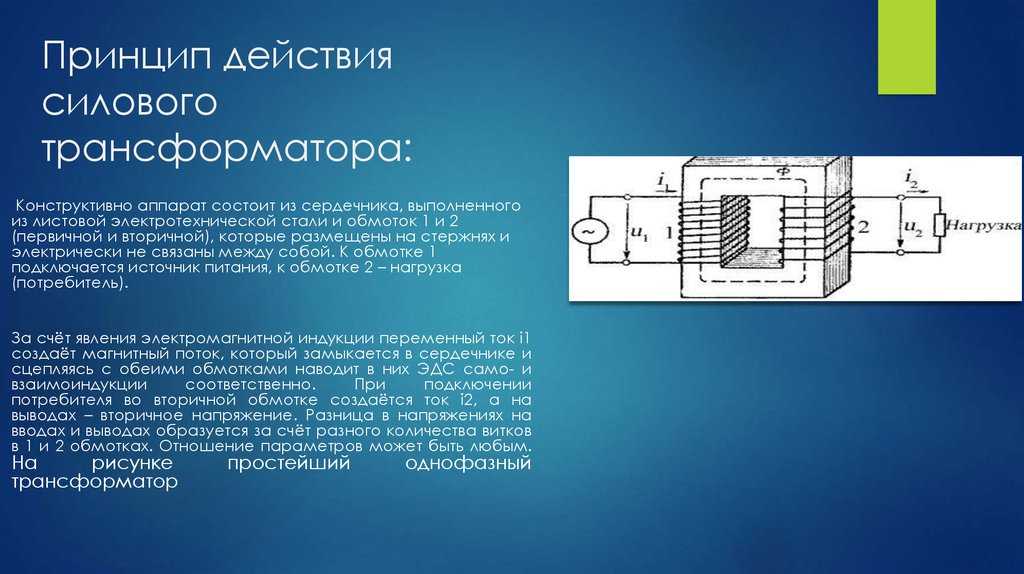 На самом деле параллельных прямых на графике бесконечно много, на чертеже показаны некоторые из них и направление движения по фазовой траектории.

Это — общее решение уравнения движения шарика. Каждая из этих фазовых траекторий доставляет минимум функционалу действия, что непосредственно следует из выкладок, проделанных выше.

Что делает автор задачи? Он говорит: вот шарик покоится, и за промежуток времени от t_A до t_B действие равно нулю. Если шарик толкнуть к стенке, то за тот же промежуток времени действие будет больше, так как у шарика отличная от нуля и неизменная кинетическая энергия. Но почему шарик движется к стенке, ведь в покое действие будет меньше? Значит ПНД испытвает проблемы и не работает! Но мы обязательно решим это в следующей статье.

То что говорит автор — бред. Почему? Да потому, что он сравнивает действия на различных ветвях одной и той же действительной фазовой траектории! Между тем, при применении ПНД, сравнивается действие на действительной траектории и на множестве окольных траекторий.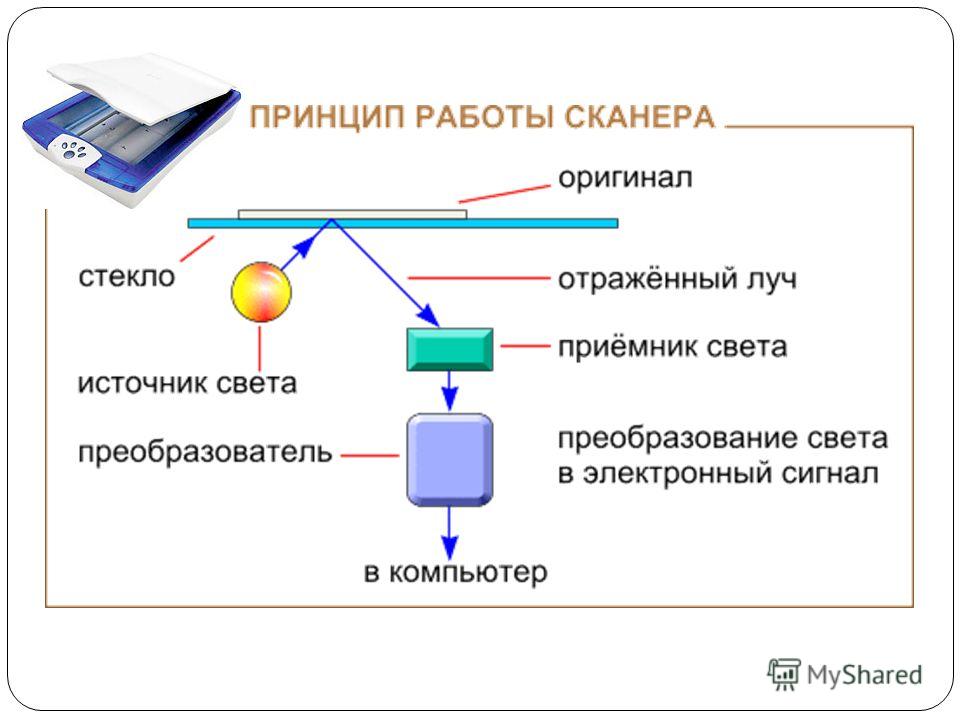 То есть происходит сравнение действия на реальной траектории с действием на тех траекториях, которых нет в природе, и никогда не будет!

Не понятно? Объясню ещё более доходчиво. Рассмотрим состояние покоя. Оно описывается ветвью фазового портрета, совпадающего с осью абсцисс. Координата не меняется с течением времени. Это действительное движение. А какое же движение будет окольным. Любое другое кинематически возможное. Например малые колебания шарика около рассматриваемого нами положения покоя. Задача допускает колебания шарика вдоль оси х? Допускает, значит такое движение кинематически возможно и может рассматриваться как одно их окольных

Почему же шарик таки покоится? Да потому, что действие в состоянии покоя, вычисленное на фиксированном промежутке времени от t_A до t_B, будет меньше действия, при малых колебаниях на том же промежутке времени. Значит колебаниям и любому другому «шевелению» шарика природа предпочитает покой. В полном соответствии с ПНД.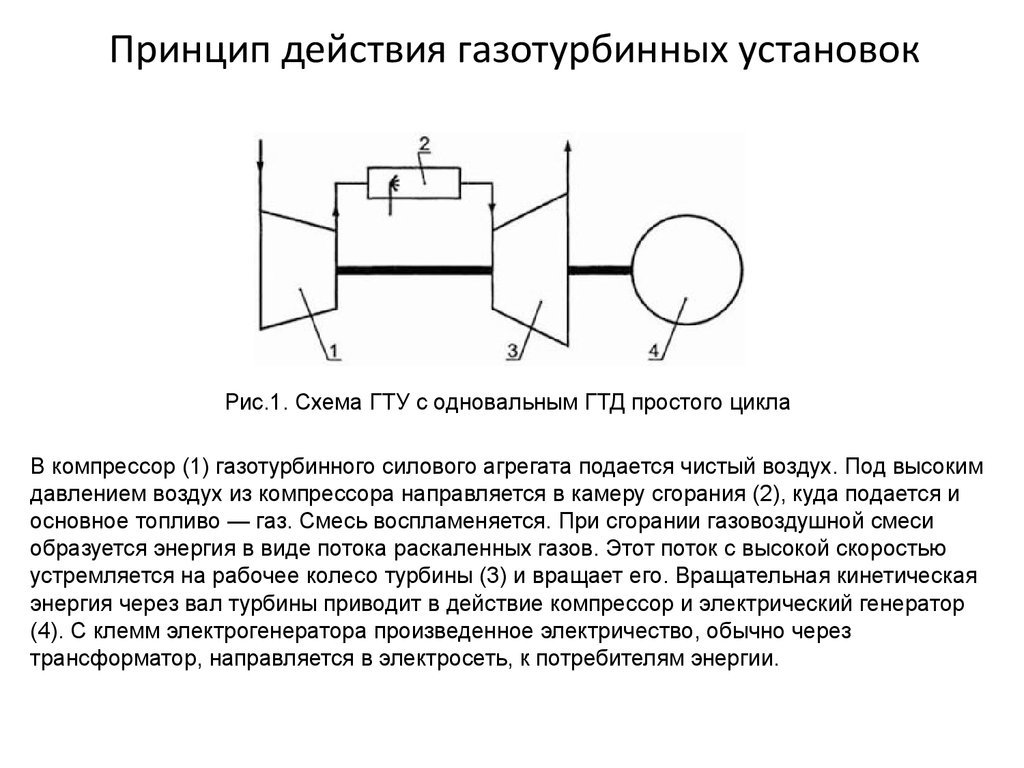

Допустим мы толкнули шарик в сторону стенки. Пусть мы толкнули его как хочет автор, со скоростью, подобранной из краевых условий, так чтобы в момент времени t_B шарик оказался в том же положении, откуда стартовал. Шарик, с постоянной скоростью долетит до стенки, упруго отскочит и вернется в начальное положение в момент времени t_B, опять таки с постоянной скоростью. Ок, это действительное движение. Какое движение будет одним из окольных? Например, если шарик будет двигаться к стенке и от стенки со скоростью, меняющейся со временем. Такое движение возможно кинематически? Возможно. Почему же модуль скорости шарика не меняется? Да потому, что действие на такой фазовой траектории будет иметь минимальное значение, в сравнении с любом другим вариантом, где скорость зависит от времени.

Вот и всё. Ничего такого волшебного тут не происходит. ПНД работает безо всяких проблем.

ПНД — фундаментальный закон природы. Из него, в частности, вытекают законы механики, например дифференциальные уравнения движения (12). ПНД говорит нам о том, что природа устроена так, что уравнение движения консервативной механической системы выглядит именно как выражение (12) и никак иначе. Большего от него и не требуется.

Не нужно придумывать проблем там где их нет.

Завоюйте доверие с помощью принципов работы

Ресурсы

Доверие является важным компонентом успешной работы. Люди лучше всего работают, когда чувствуют, что могут доверять своему начальству и окружающим. И наоборот, без этой связи доверия сотрудники не выйдут за пределы минимума, необходимого для выполнения их работы. Это имеет смысл, но как построить доверие на рабочем месте?

Для укрепления доверия используются многие ингредиенты, включая честность, последовательность, уважительное общение, предсказуемость и надежные действия с течением времени. Совместное создание принципов работы — это ощутимая деятельность, которая может помочь рабочей группе установить и развить атмосферу доверия.

Принципы работы — это письменные заявления, описывающие, как члены группы будут взаимодействовать друг с другом и с теми, кого они обслуживают — клиентами, заказчиками, участниками. Принципы работы переводят ценности и убеждения в конкретные действия. Это не то же самое, что ценностное предложение организации, такое как «Мы ​​подаем только самые свежие экологически чистые продукты» или «Мы каждый раз будем отправлять вам вашу покупку вовремя». Это обещания заказчику, клиенту или покупателю, и они необходимы, но разные. Принципы работы касаются повседневного поведения сотрудников.

«Принципы ведения бизнеса — это правила поведения, которые позволяют людям знать, что разрешено, а что запрещено — в их компаниях и на рабочих местах. Принципы работы могут служить руководством, помогая людям принимать правильные решения, укрепляя доверие и способствуя инновациям» (Lynch, 2008).

У Google есть десять принципов работы, один из которых: «Вы можете быть серьезными без костюма». Одна из основных ценностей Whole Foods Market, Inc. для членов команды гласит: «Мы берем на себя ответственность за собственные успехи и неудачи. Мы празднуем успехи и рассматриваем неудачи как возможности для роста…»

Компания Raymond Management Group в Мэдисоне, штат Висконсин, которая управляет большой сетью отелей и объектов недвижимости, определила 10 принципов работы:

1. Не сплетничать не слушайте сплетни.
2. Перейти к источнику; Решите проблему . Лучший способ решить проблему — обратиться непосредственно к источнику предполагаемой проблемы. Поговорите в открытой и позитивной манере и найдите взаимовыгодное решение.
3. Будьте активны – возьмите на себя ответственность – Удивительно, чего можно добиться, когда каждый чувствует: «Если это произойдет, то это зависит от меня!» Берите на себя инициативу во всех аспектах своей работы и ищите в компании возможности помочь товарищам по команде.
4. Создайте культуру аплодисментов – Отмечайте успехи, как большие, так и маленькие, как публично, так и в частном порядке.
5. Заслужить уважение; Проявите уважение — Настоящее и прочное уважение нельзя навязать, его нужно заслужить.
6. Никаких неожиданностей . Неожиданности — это сигналы о том, что наши структуры, процессы и/или командная работа неадекватны. Чтобы свести к минимуму неожиданности, нужная информация должна попасть к нужным людям в нужное время, чтобы они могли предпринять правильные действия для получения правильных результатов.
7. Закрытие – Закрытие означает, что каждый берет на себя ответственность за выполнение задачи, проблемы или проблемы.
8. Постановка задачи; Предложите решение . Приучите себя к тому, что всякий раз, когда у вас есть критика, беспокойство, вопрос или проблема, выделите еще несколько секунд, чтобы обдумать вашу рекомендацию, ваши предложения по улучшению или решению.
9. Выберите свое отношение – Возьмите на себя полную ответственность за выбор своего отношения. В одно мгновение мы можем изменить весь наш день. Это решение, которое мы принимаем.
10. Развлекайтесь – Получая удовольствие от работы, мы получаем от нее удовольствие. Юмор настраивает нас на позитивный лад, позволяет нам справляться со стрессом и естественным образом настраивает нас на предоставление качественных услуг клиентам и коллегам

В Raymond Management group эти принципы обсуждаются как в домашнем офисе, так и в отелях.

Принципы работы могут быть очень хорошим клеем для создания доверительной, сплоченной и взаимоподдерживающей рабочей среды. Однако они полезны только в том случае, если все, от высшего руководства до самого нового сотрудника, обращают на них внимание. Экономист Кей Плантес (Plantes & Finfrock, 2009, стр. 159–160) использует термин «руководящие принципы» и говорит:

Не существует единого набора «правильных» руководящих принципов; важно то, что на них действуют, а не на показные заявления. Лидеры должны искренне пытаться смоделировать руководящие принципы своими действиями и словами, чтобы вокруг этих принципов не возникло никакого цинизма. Вы знаете, что у вас есть сильный руководящий принцип, когда люди не стесняются в любое время сказать любому другому сотруднику, включая начальника: «Ваши действия не соответствуют нашим согласованным ценностям» (стр. 159).-160)

Я использую процесс, состоящий из двух частей, чтобы помочь группам определить свои принципы работы. В первой части участники в парах беседуют друг с другом о ситуации, когда, по их мнению, организация была «на высоте». Затем мы в группе обсуждаем ценности, лежащие в основе этих памятных ситуаций. Во-вторых, участники молча отвечают на такой вопрос, как «Какое повседневное поведение между нами как сотрудниками и между нами и теми, кому мы служим, демонстрирует наши ценности?» Участники молча генерируют свои собственные идеи на бумаге, а затем соглашаются в своей небольшой группе. Процесс категоризации Майкл Уилкинсон описывает в Секреты фасилитации идеально подходит для группировки поведений и совместного решения, как их назвать.

Я призываю своих клиентов не ожидать совершенства. У всех будут «промахи», и они будут совершать ошибки, а иногда и действовать совершенно не в соответствии с принципами работы. Важно признать оплошность, извиниться, если необходимо, и двигаться вперед с новыми обязательствами.

Ресурсы

Плантес М.К. и Финфрок Р. (2009). Beyond Price: дифференциация вашей компании действительно важными способами . Остин, Техас: Greenleaf Book Group Press.

Наша философия: десять вещей, которые, как мы знаем, являются правдой (сентябрь 2009 г.) По состоянию на 13 февраля 2011 г. по адресу http://www.google.com/corporate/tenthings.html.

Штаубус М. и Линч Р.П. Построение системы доверия: десять скрытых секретов успеха в компаниях, принадлежащих сотрудникам. По состоянию на 13 февраля 2011 г. по адресу http://rady.ucsd.edu/beyster/newsletter/2010/fall/system-trust2.html .

Уилкинсон, М. (2004). Секреты фасилитации: S.M.A.R.T. руководство по получению результатов с группами. Сан-Франциско: Джосси-Басс.

Хотите узнать больше о методах фасилитации? Ознакомьтесь с нашим курсом «Эффективный фасилитатор ».

Свяжитесь с нами Об обучении и услугах по фасилитации »

Принципы работы: что это такое и как их использовать

Принципы работы, или, как их часто называют, операционная система компании чтобы организации применяли свои ценности на практике и добивались цели.

Многие компании полагаются на принципы работы, чтобы выполнять задачи быстрее. Они также влияют на культуру и ценности. Colorcon заявляет, что их принципы работы «определяют нашу культуру, ценности и организацию». Wistia использует несколько иную точку зрения, заявляя, что их операционная система представляет собой «новую методологию того, как Wistia выполняет работу».

Могут существовать разные определения принципов работы, но ясно, что компании используют их для создания общекорпоративной направленности и понимания того, каковы долгосрочные «общие» цели организации.

Зачем и когда использовать принципы работы

Принимая решение использовать принципы работы, вы делаете гораздо больше, чем просто создаете еще одну версию своей предыдущей бизнес-стратегии или процессов.

Принципы работы дают вам возможность четко указать, что не следует делать, а что следует делать. Это важная деталь, которую следует учитывать. Давайте рассмотрим пример из работы Боггиса и Траффорда о том, как принципы работы могут формировать осмысленную стратегию.

Они относятся к ситуации, в которой бизнес предпочитает использовать операционный принцип «Мы продолжаем органически расти», вместо: «Мы растем за счет приобретения». Заявляя, что бизнес предпочитает что-то одно, а не альтернативу, они ясно формулируют, как они хотят проводить свое время. Это может быть освобождением для сотрудников: это определяет область работы, которая не требует времени или внимания.

Используя принципы работы, вы можете создать стратегию, которая будет иметь больше смысла для ваших сотрудников и, как предлагают Боггис и Траффорд, действительно значимую стратегию. Такой подход к стратегии может быть полезен менеджерам или лидерам, которые хотят ясно изложить свои ожидания и долгосрочные устремления, а принципы работы предлагают руководство о том, как каждый может внести свой вклад своими решениями и действиями.

Какое отношение альпинизм имеет к принципам работы?

Wistia, представляя свою «операционную систему», обнаружила, что альпинизм был полезной метафорой для их команды, чтобы показать, как именно они хотят, чтобы они выполняли свою работу ежедневно и еженедельно.

По словам Эда Виестурса, единственного американца, покорившего все четырнадцать самых легендарных гор мира, альпинизм заключается в том, чтобы «координировать обязанности и идти в ногу со своей командой альпинистов».

Wistia взяла этот подход и применила его при разработке своей продукции. Результат? Операционная система, использующая стратегию базового лагеря и вершины. Во время базового лагеря члены команды изучают новые идеи и раскрывают свой творческий потенциал. Как только они начнут «саммит», у каждого человека будет серия экспедиций (в основном задач), которые они должны выполнить, чтобы вся компания достигла пика (завершила проект).

Компания Wistia считает, что операционная система — это их ответ на вопрос сохранения гибкости бизнеса даже по мере его роста. Принцип работы «короткими, контролируемыми импульсами с высокочастотной обратной связью» означает, что они могут сохранять контроль над тем, как их компания и продукт развиваются с течением времени.

Как на самом деле выглядят принципы работы?

Мы привели несколько примеров того, как разные организации определяют конкретные принципы работы и почему они их ввели. Теперь давайте посмотрим, как на самом деле выглядят принципы работы.

Tettra

В этом посте об операционной системе Tettra мы делимся нашими собственными принципами работы, а также нашими основными ценностями. Мы также делимся подробностями о том, как мы используем эту систему на ежедневной основе. Наконец, мы предлагаем передовой опыт по сборке собственной операционной системы. Это включает в себя детали того, как привлечь всех, а также как определить непосредственно ответственного человека, который в конечном итоге несет ответственность за завершение работы над системой.

Fort Wayne Metals

Fort Wayne Metals перечисляет свои семь принципов работы после ценностей своей компании. Их ценности и принципы работы играют большую роль в привлечении талантов и помогают кандидатам определить, подходят ли они для компании. Например:

Принцип работы: «Каждый должен нести ответственность за то, чтобы каждый день максимально раскрывать свой потенциал: Мы можем достичь наших целей только в том случае, если каждый каждый день сосредоточен на своих обязанностях. Делать меньше — значит не уважать своих коллег, каждый должен участвовать, чтобы раскрыть свой потенциал».

Калифорнийский университет, Беркли

Беркли также имеет ряд принципов работы, которые связаны с их ценностями. Например:

Принцип работы: «Мы упрощаем: мы сокращаем ненужные шаги и упрощаем выполнение задач. Наши решения являются общими там, где они могут быть, и индивидуальными там, где это важно».

Как документировать и заручиться поддержкой принципов работы

Если вы считаете, что вашей организации сложно превратить ценности в действия и результаты, стоит подумать о внедрении собственных принципов работы. Попробуйте провести семинар, чтобы определить свои основные ценности и принципы работы. Мы даже создали шаблон, который вы можете использовать для проведения этого семинара с вашей командой.

Вот другие шаги, которые могут помочь в этом процессе:

1. Спросите себя (или проведите мозговой штурм с коллегой): «Как это выглядит изо дня в день?» «Как это звучит?» Например, основная ценность «сотрудничество» может выглядеть так, будто люди из разных команд сидят вместе за обедом. Это может звучать так, будто кто-то спрашивает: «Эй, могу я дать тебе кое-что для проверки?» Хотя это может показаться глупым, представление реальных примеров поможет вам определить, как вы хотите, чтобы компания работала.