Содержание
Расстояние Между Концами Циркуля 7 Букв
Решение этого кроссворда состоит из 7 букв длиной и начинается с буквы Р
Ниже вы найдете правильный ответ на Расстояние между концами циркуля 7 букв, если вам нужна дополнительная помощь в завершении кроссворда, продолжайте навигацию и воспользуйтесь нашей функцией поиска.
ответ на кроссворд и сканворд
Понедельник, 22 Апреля 2019 Г.
РАСТВОР
предыдущий
следующий
ты знаешь ответ ?
ответ:
связанные кроссворды
- Раствор
- Угол, образуемый раздвинутыми концами чего-либо (ножками циркуля, лезвиями ножниц)
- Раствор
- Тестообразная смесь цемента, песка и воды 7 букв
- Водка по своей физической сущности 7 букв
- Жидкость, о объему которой равномерно распределено другое вещество 7 букв
- Одна из дверей в их сплошном ряду 7 букв
- Однородная смесь компонентов 7 букв
похожие кроссворды
- Расстояние между концами крыльев самолёта
- Струна между концами метательного лука
- Ненормальное (увеличенное) расстояние между двумя парными органами
- Расстояние между передними узловыми точками глаз
- Расстояние между центрами зрачков глаз
- Максимальное расстояние между ногами при ходьбе
- Наименьшее расстояние между звуками по высоте
- Расстояние между колосниками
- Расстояние между двумя железнодорожными путями
- Расстояние, пространство между двумя трамвайными или железнодорожными путями
- Расстояние между строками
- Расстояние между двумя отметками на измерительной шкале 7 букв
- Черта, обозначающая расстояние между участниками дуэли 6 букв
- Промежуток, расстояние между чем-либо 8 букв
Отрезок.
 Длина и середина отрезка. Сравнение отрезков
Длина и середина отрезка. Сравнение отрезков
- Длина отрезка
- Равные отрезки
- Сравнение отрезков
- Середина отрезка
Отрезок — это часть прямой, ограниченная двумя точками, лежащими на этой прямой. Точки, определяющие границы отрезка, называются концами отрезка.
Отрезок обозначается двумя большими латинскими буквами, поставленными при его концах: отрезок AB или BA.
Длина отрезка
Длина отрезка — это расстояние между концами отрезка. Любой отрезок имеет длину, бо́льшую нуля:
Измерение длины отрезка осуществляется путём сравнения данного отрезка с длиной единичного отрезка. Единичный отрезок — это отрезок, длина которого принимается за единицу. Следовательно:
длина отрезка – это положительное число, показывающее, сколько раз единичный отрезок и его части укладываются в данном отрезке.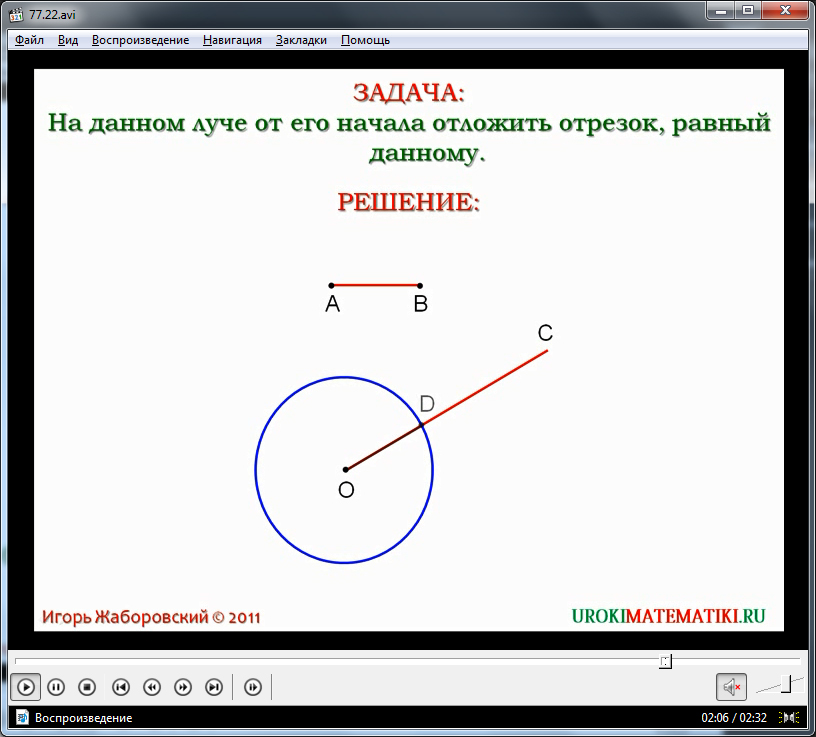
Чаще всего используются единичные отрезки равные 1 мм, 1 см, 1 дм, 1 м или 1 км. Измерить длину отрезка можно линейкой или любым другим прибором для измерения длины:
AB = 6 см.
Свойства длин отрезков:
- Основное свойство длины отрезка: если точка делит отрезок на два отрезка, длина всего отрезка равна сумме длин этих двух отрезков.
- Длины равных отрезков равны.
- Любой отрезок имеет определённую длину, большую нуля.
Равные отрезки
Равные отрезки — это отрезки, имеющие одинаковую длину. Если наложить равные отрезки друг на друга, то их концы совпадут.
Пример. Возьмём два отрезка CD и LM:
Если расположить отрезки параллельно друг над другом так, чтобы точка C была над точкой L, то станет видно, что точка D располагается над точкой М:
Значит длины отрезков равны, следовательно CD = LM.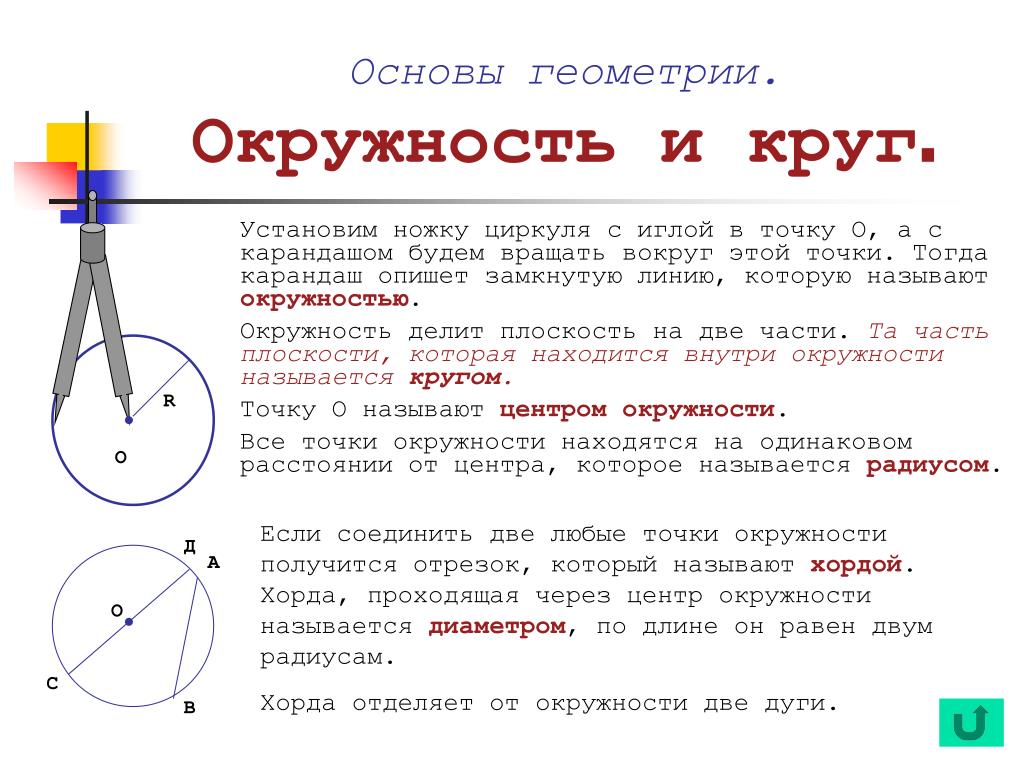
Сравнение отрезков
Сравнить два отрезка — это значит определить, равны они, или один больше другого.
Сравнить два отрезка можно, отложив на прямой оба отрезка из одной точки в одну и туже сторону. Для этого можно воспользоваться циркулем.
Чтобы отложить на прямой отрезок равный данному, сначала помещают ножки циркуля так, чтобы острия их концов упирались в концы отрезка, а затем, не изменяя раствора циркуля, переносят его так, чтобы оба его конца находились на прямой.
При сравнении двух отрезков возможно получение одного из представленных результатов: отрезки будут равны, первый отрезок будет больше второго или первый отрезок будет меньше второго.
Пример. Если отложить на прямой от любой точки, например C, в одну сторону два отрезка CA и CB и точка A окажется между точками C и B, то отрезок CA меньше отрезка CB (или CB больше отрезка CA):
CA < CB или CB > CA.
Если точка B окажется между точками C и A, то отрезок CA больше отрезка CB (или CB меньше отрезка CA):
CA > CB или CB < CA.
Если точки A и B совпадут, то отрезки CA и CB равны:
CA = CB.
Если при наложении отрезков оба их конца совмещаются, значит отрезки равны.
При сравнении отрезков путём измерения их длин больше будет тот отрезок, у которого больше длина.
Пример. Сравнить длину отрезков AB и AC.
Так как отрезок AB имеет большую длину, чем отрезок AC, то
AB > AC.
Так как отрезки AB и AC имеют одинаковую длину, то
AB = AC.
Если при измерении отрезков их длины равны, то и отрезки равны.
Середина отрезка
Середина отрезка — это точка, делящая отрезок на две равные части.
Использование компаса и шагов
Публикации расширения штата Северная Каролина
Просмотреть заметки владельца Woodland
Компас и определение шага могут быть полезны во многих различных мероприятиях на лесных участках. Компас может указать направление, в котором вы движетесь относительно магнитного севера, а шаг — это простое средство измерения линейного расстояния при ходьбе. Сочетание использования компаса с шагом поможет вам в путешествии по стране или пересечении границ собственности.
Как только вы научитесь пользоваться компасом, вы сможете определять, где находится магнитный север и где вы находитесь относительно того места, где вы хотите быть (например, находится ли эта область к югу или западу от дома). Чтобы добиться успеха в стимуляции, вам нужно знать, какое расстояние вы преодолеваете в своем темпе. Следующее поможет вам использовать компас, чтобы определить направление и определить свой темп.
Компас
Перейти к Компасу
Компас состоит из нескольких основных частей (Рисунок 1).
- Стрелка компаса, часто красно-черная или красно-белая, всегда указывает на северный магнитный полюс Земли. Эта магнитная стрелка свободно плавает, если компас удерживается горизонтально (параллельно земле).
- На корпусе компаса есть цифры, деления и буквы. Числа идут от 0 до 360, представляя количество градусов в круге. Буквы N, S, E и W обозначают север, юг, восток и запад.
- На опорной плите есть стрелка направления движения. Вы указываете стрелку направления движения в том направлении, в котором хотите двигаться.
- Некоторые компасы имеют отметки в дюймах или миллиметрах на краю компаса. Они используются с масштабом карты для определения расстояния между двумя точками. Это не рассматривается в данной публикации.
Чтобы пользоваться компасом (рис. 2), его необходимо держать ровно и держать подальше от металла. Положите компас на ладонь одной руки и положите эту руку на ладонь другой руки. Плотно прижмите локти к бокам.
Плотно прижмите локти к бокам.
Поскольку стрелка компаса чувствительна к металлу, снимите металлические пряжки с ремней, кольца и часы и держитесь подальше от металлических заборов, автомобилей и т. д., чтобы исключить ложные показания.
Удерживая уровень компаса, направьте стрелку направления движения в нужном направлении. Затем поворачивайте корпус компаса до тех пор, пока стрелка компаса не совместится со стрелками, нарисованными в нижней части компаса. Помните, что цветной конец стрелки компаса указывает на север. Теперь двигайтесь так, чтобы смотреть прямо вперед в том направлении, в котором вы хотите двигаться. Убедитесь, что магнитная стрелка по-прежнему указывает на север.
Чтобы не отклоняться слишком далеко влево или вправо от направления движения, выберите объект как можно дальше для выравнивания. Время от времени останавливайтесь, чтобы убедиться, что вы движетесь в правильном направлении. Продолжайте повторять этот процесс, чтобы оставаться на курсе.
Рисунок 1. Основные части компаса.
Изображение для печати
Рис. 2. Как держать компас.
Изображение для печати
Шаг
Перейти к шагу
Шаг — это простой метод измерения линейного расстояния при ходьбе. Один темп равен двум шагам, начинающимся и заканчивающимся ведущей ногой (рис. 3). Чтобы определить свой темп, попрактикуйтесь в многократной ходьбе обычным шагом по размеренной дистанции. Шагните по трассе несколько раз, чтобы определить свой средний темп, а затем используйте приведенную ниже таблицу темпа, чтобы определить расстояние в каждом темпе.
| шагов / 66 футов | Футы/шаг | Шагов / 66 футов | Футы/шаг | Шагов / 66 футов | Футы/шаг | Шагов / 66 футов | Футы/шаг |
| 10,0 | 6,60 | 13,5 | 4,89 | 16,5 | 4,00 | 19,5 | 3,38 |
| 10,5 | 6,28 | 14,0 | 4,71 | 17,0 | 3,88 | 20,5 | 3,22 |
| 11,5 | 5,74 | 14,5 | 4,55 | 17,5 | 3,77 | 21,0 | 3,14 |
| 12,0 | 5,50 | 15,0 | 4,40 | 18,0 | 3,67 | 21,5 | 3,07 |
| 12,5 | 5,28 | 15,5 | 4,26 | 18,5 | 3,57 | 22,0 | 3,00 |
| 13,0 | 5,08 | 16,0 | 4,13 | 19,0 | 3,47 | 22,5 | 2,93 |
В лесном хозяйстве измерение шага обычно используется для измерения высоты деревьев. Это обсуждается в примечании владельца лесного фонда 5, Оценка объема стоящего дерева с помощью линейки весов (Билтмор) . Ниже перечислены указания по определению вашего темпа на трассе длиной 66 футов.
Это обсуждается в примечании владельца лесного фонда 5, Оценка объема стоящего дерева с помощью линейки весов (Билтмор) . Ниже перечислены указания по определению вашего темпа на трассе длиной 66 футов.
- Измерьте 66-футовую трассу на ровной поверхности с помощью рулетки. Используйте этот курс, чтобы определить точность вашего темпа.
- Пройдите этот курс три или четыре раза. Сравните результаты. Убедитесь, что все одинаковы и шаги в каждом темпе соответствуют вашему шагу.
- Используя таблицу шагов, определите, сколько погонных футов охватывает каждый из ваших шагов. Например, если вам требуется 13 шагов, чтобы преодолеть 66 футов, то каждый из ваших шагов равен 5,08 фута.
- При переходе из одной точки в другую, где вы не знаете расстояние, пройдите расстояние. Запишите количество шагов, а затем умножьте на длину вашего шага. Например, если вам требуется 20 шагов, чтобы преодолеть неизвестное расстояние, умножьте ваш известный темп (скажем, 5,08 фута) на 20 шагов, чтобы получить 101,6 фута.

На ровной открытой местности темп может быть достаточно точным при тренировке. Но на склонах и в кустарниковых или каменистых местах его точность снижается. На труднопроходимой местности не пытайтесь поддерживать стандартный темп. Вместо этого допускайте неизбежное сокращение вашего темпа (как в гору, так и в гору), повторяя счет через определенные промежутки времени. Например, на умеренных склонах считайте каждый десятый шаг дважды: 1,…,9., 10, 10, 11. На более крутых склонах может потребоваться повторение каждого пятого счета: 1,…, 4, 5, 5, 6. На самых крутых склонах, в очень густом кустарнике, на болотах или среди валунов, каждый счет, возможно, придется повторить. Стабильная точность стимуляции в таких условиях достигается только практикой и поддерживается только постоянной проверкой.
Если вы потренируетесь пользоваться компасом и потратите время на определение своего темпа, вы обнаружите, что путешествовать по лесу намного проще. Помните, чтобы успешно пользоваться компасом и темпом, вам нужно практиковаться.
Рисунок 3. Иллюстрация шага и темпа.
Изображение для печати
- Роберт Бардон
Заместитель декана дополнительного образования, руководитель отдела дополнительного образования и профессор
Лесного хозяйства и экологических ресурсов
- Ключевые слова:
- Лесные инструменты
- Измерения леса
- Шаг
- Компас
Дополнительную информацию можно найти на следующих веб-сайтах расширения штата Северная Каролина:
Extension Forestry
Дата публикации: 1 января 2007 г.
ВОН-39
NC Cooperative Extension запрещает дискриминацию и домогательства независимо от возраста, цвета кожи, инвалидности, семейного и семейного положения, гендерной идентичности, национального происхождения, политических убеждений, расы, религии, пола (включая беременность), сексуальной ориентации и статуса ветерана.
Как пользоваться и читать показания компаса
Перейти к содержимому
Перейти в меню
Войти / зарегистрироваться
Показать поиск
Народная вера
Ребенок с компасом в саду аббатства Англси, Кембриджшир.
© National Trust Images/Britainonview/Дэвид Левенсон
Многие люди используют свои мобильные телефоны и спутниковые навигаторы, чтобы передвигаться, но также полезно знать, как работает компас, на тот случай, если вы находитесь где-то далеко, где нет сигнала или если у вас низкий заряд батареи. Кроме того, это веселее.
Кроме того, это веселее.
Вот наши главные советы о том, как читать по компасу, взятые из нашей книги Go Wild in the Woods Голди Хоук и Рэйчел Сондерс.
Полезно знать
Есть несколько важных вещей, которые вы должны знать о том, как работает компас, прежде чем использовать его в дикой природе.
На вашем компасе есть четыре основных направления: север, юг, восток и запад. По всему компасу есть небольшие измерения, называемые градусами.
Наиболее важной частью компаса является магнитная стрелка. Он вращается вокруг компаса, когда вы двигаетесь, но красный конец всегда будет указывать на север, а белый (или иногда черный) конец всегда будет указывать на юг. На корпусе также есть стрелка (см. рисунок ниже), известная как «стрелка ориентации», и стрелка на опорной плите, называемая «стрелка направления движения».
Поверните циферблат компаса так, чтобы ориентирующая стрелка совпала с красным концом магнитной стрелки.
Поверните циферблат компаса так, чтобы ориентирующая стрелка совпала с красным концом магнитной стрелки.
Как следовать компасу
Если вы хотите идти в точном направлении, вы можете «следовать по азимуту». Чтобы следить за азимутом, все, что вам нужно сделать, это:
- Положите компас на ладонь так, чтобы стрелка направления движения указывала туда, куда вы хотите попасть.
- Поверните шкалу компаса так, чтобы ориентирующая стрелка совпала с красным концом магнитной стрелки.
- Стрелка направления движения должна совпадать с вашим «азимутом» (это угол, под которым вы хотите идти) — теперь вы можете начать свою прогулку, следуя этой стрелке.
- Если вы беспокоитесь, что сбились с пути, совместите стрелку-ориентир с иглой. Всякий раз, когда вы делаете это, ваша стрелка направления движения будет указывать на то, куда вы хотите попасть (однако не забывайте держать шкалу компаса в том же положении).


