Школа шгн расшифровка: Подробнее про школы городского набора (ШГН)

Содержание

Подробнее про школы городского набора (ШГН)

Что такое школы городского набора?

Школы городского набора – это центры интенсивной профильной подготовки. В них принимают детей, преимущественно начиная с 5-го класса, так как к этому возрасту ребята уже адаптировались к школьному обучению и попробовали свои силы в разных направлениях.

Школы городского набора – это:

Президентский физико-математический лицей №239
М. «Чернышевская», ул. Кирочная, д. 8
Принимают в 5, 8 и 10 классы
https://239.ru/postupay

Губернаторский физико-математический лицей № 30»
Принимают в 5, 8 классы
https://www.school30.spb.ru/rinvite.shtml

Юношеская математическая школа (ЮМШ)
М. «Новочеркасская», Таллинская ул., д. 26, к. 2
Принимают в 5, 8 классы
http://yumsh.ru/cms/classes/5class   http://yumsh.ru/cms/classes/class8

Аничков лицей
М. «Невский пр.», Невский пр., д. 39, лит. А
Принимают в 8 класс: http://anichkov. ru/page/inlicey/

Академический лицей «Физико-техническая школа» им. Ж. И. Алфёрова
М. «Пл. Мужества», ул. Хлопина, д. 8, к. 3, литера «А»
Принимают в 8 класс
http://www.school.ioffe.ru/school/admission/

Лаборатория непрерывного математического образования (ЛНМО)
Принимают в 5-8 классы
https://lnmo.ru/dni_otkritich_dverei_lnmo

Санкт-Петербургская классическая гимназия №610
Принимают в 5 класс: https://610.ru/school/howtoget.html

Академическая гимназия имени Д. К. Фаддеева Санкт-Петербургского государственного университета
Принимают в 8 класс
https://spbu.ru/postupayushchim/programms/obshcheeobr..

Кроме того, существуют районные школы, которые не осуществляют общий целенаправленный набор детей со всего города, однако поступить туда также можно, пройдя вступительные испытания или даже не делая этого. Уровень и качество образования в них выше, чем в других районных школах, но в среднем ниже, чем в профильных ШГН. Информацию, связанную с правилами поступления, можно узнать на сайтах школ или по телефону.

Зачем переходить в школу городского набора?

Эти школы многие годы возглавляют российские рейтинги по результатам ЕГЭ и олимпиад. Так, физико-математический лицей № 239 уже третий год признаётся лучшей школой России, а ещё несколько питерских школ входят в топ-100. Все это не случайно, ведь уровень образования в этих школах значительно выше, нежели в обычных общеобразовательных учреждениях.

Только ли уровень образования отличается от обычных школ?

Конечно, нет. Выпускники таких заведений с гордостью могут рассказать вам о необыкновенной атмосфере, наполняющей эти школы. Это тот случай, когда школа действительно становится вторым домом, ведь внеурочная жизнь крайне обширна: от походов с палатками в горы, балов, спектаклей собственной постановки до новогодних костюмированных флеш-мобов, ресторанных дней и дней науки с приглашёнными учеными, в том числе нобелевскими лауреатами. В этих школах большое количество бесплатных кружков и курсов на любой вкус: спортивные секции, лучшие в городе научные центры, кружки видеосъемки, фотографии, робототехники и многое другое.

Как проходит отбор в школы городского набора?

Набор в такие школы происходит на конкурсной основе: необходимо пройти вступительные испытания. Для того, чтобы успешно сдать экзамен, необходимо уверенно владеть школьной программой, не бояться и уметь решать нестандартные олимпиадные задачи и, кроме того, уметь оформлять свои мысли в связный ясный текст решения.

Почему стоит заниматься именно у нас?

Мы готовим к поступлению наших учеников уже многие годы и делаем это весьма успешно: большинство выпускников Фрактала поступают в школы городского набора в 5 или в 8 класс и продолжают обучение там вплоть до выпуска и поступления в самые престижные вузы страны! Некоторые ребята успешно справляются с вступительными испытаниями в 5 класс уже в 3 классе, чем обеспечивают себе поступление без олимпиады на следующий год.

Вступительные испытания в 5 класс чаще всего проводятся по математике и русскому языку. Но в некоторых школах бывает еще проверка эрудиции, знаний по английскому языку, собеседование. Мы готовим к вступительным испытаниям по математике, с небольшим включением заданий по лингвистике и работе с текстом.

Мы разрабатываем программу наших курсов исходя из вступительных испытаний во все школы городского набора, поэтому наши занятия помогут Вашему ребёнку подготовиться к максимальному количеству различных заданий. В отличие от курсов непосредственно в самих школах, мы не просто обеспечиваем целенаправленную подготовку, состоящую по большей части из постановки навыков решения типовых задач и обучения наиболее часто встречающимся олимпиадным темам. Мы стараемся научить ребёнка думать над заданиями, которые он видит впервые, а не только решать задачи, которые он уже умеет решать.

Кроме этого мы проводим несколько срезовых работ: в начале, середине и конце курса, что позволяет отследить прогресс каждого ученика, а также мотивирует детей, которые могут видеть свои успехи. Помимо тематических занятий по математике, в курс включены блоки, направленные на улучшение внимания и концентрации, анализ информации, развитие эрудиции и нестандартного мышления. Это не только полезно для поступления, но и очень интересно! На заочном курсе также разработана система мотивации и отслеживания своих успехов, которая помогает, несмотря на отсутствие личного контакта с преподавателем, успешно двигаться в нужном направлении и не терять интерес к занятиям.

Хочется отметить, что мы не даём гарантий и не можем обеспечить поступление в нужную Вам школу, однако мы сделаем все возможное для того, чтобы наши ученики развили в себе определённые умения, обрели необходимые знания и повысили свой уровень в решении заданий вступительных олимпиад.

особенности программ,отличие лицея, разница в россии

В России существуют разные образовательные учреждения, в особенностях которых хорошо разбираются не все. Так, многие родители не знают, чем отличается лицей от гимназии, ошибочно думая, что в первом случае получают техническое образование, а во втором — гуманитарное. На самом деле это не совсем так.

Общее образование можно получить и в средней общеобразовательной школе (СОШ), но почти каждый родитель считает своего отпрыска умным и способным ребенком, поэтому старается пристроить его в такое учебное заведение, где уровень полученных знаний будет выше. Но там и нагрузка на учеников значительно больше, поскольку практикуется углубленное изучение предметов.

Ступени образования в России

Каждый россиянин обязательно проходит несколько стадий обучения. Согласно закону «Об образовании», уровень полученных знаний должен быть адекватным современным требованиям, соответствующим образовательной картине мира.

В России существуют следующие ступени образования:

  • начальное общее;
  • основное общее;
  • среднее (полное) общее;
  • начальное профессиональное.

Право получить любое из вышеуказанных образований имеет каждый гражданин РФ. Наряду со ступенями установлены образовательные цензы (уровни). Начального образования в этом списке нет. Первые 3 позиции соответствуют ступеням образования: основному общему, среднему общему, начальному профессиональному.

Далее идут:

  • среднее профессиональное;
  • высшее профессиональное;
  • послевузовское профессиональное.

Другими словами, самый первый образовательный этап — это дошкольное образование, дающее возможность подготовить ребенка к СОШ. Способные ученики могут продолжить обучение в гимназии или лицее. После окончания 9 класса появляется возможность получить профессиональное образование в профильном училище, став, например, токарем или машинистом тепловоза.

А можно поступить в колледж, продолжая получать теоретические знания. После 11 класса выпускники, как правило, стремятся отдать документы в ВУЗ или университет, чтобы пройти обучение и получить диплом специалиста с высшим образованием.

После института самые способные студенты заканчивают аспирантуру, идут в академию, защищают кандидатскую диссертацию и получают ученую степень. Так что, образовываться можно очень долго, было бы желание и способности, а учебных заведений в России хватает.

Чем отличается лицей от гимназии

Отличие лицея от школы заключается в более высоком уровне образования, которое чаще всего является профильным.

От гимназии он тоже отличается целым рядом специфических особенностей:

  • технический профиль;
  • приоритетное значение практических занятий;
  • выпускник получает профильные знания и определенную специальность;
  • занятия ведут педагоги ВУЗа;
  • принимают детей после 7—8 класса;
  • выпускники имеют преимущество перед сверстниками из общеобразовательных школ при поступлении в ВУЗ.

Некоторые лицеи заключают договор с ВУЗом, согласно которому выпускники сразу становятся второкурсниками института.

Обычное школьное образование

Среднее образование считается в России обязательным, поэтому получить его должен каждый гражданин РФ. Это базовый уровень знаний, получив который, каждый решает сам, продолжать его дальше или начать осваивать рабочую специальность. Любой из вариантов имеет свои преимущества.

Сколько лет учатся в школе

Все ученики обязаны закончить 9 классов. Дальше перед школьниками встает выбор: посещать школу дальше или продолжать получать образование (а зачастую и профессию) в другом месте — профессиональном училище или колледже. Обычно после того как часть девятиклассников покинет школу, из двух девятых классов формируют один 10-й. Оставшиеся школьники учатся дальше.

Помимо обязательного посещения уроков, в школе работают кружки, спортивные секции, факультативы, где ребята могут собраться по интересам, а также подтянуть успеваемость по отдельным предметам, например, иностранному языку. В спортзале после уроков школьники совершенствуют свои навыки в определенных видах спорта.

Общеобразовательная школа — это первая ступень на пути становления личности, предоставляющая школьникам широкие возможности.

Преимущества среднего образования:

  • получение базовых знаний по общим предметам;
  • уроки физкультуры формируют и развивают тело;
  • школьники учатся коммуникабельности;
  • формируется умение жить в коллективе и работать в команде;
  • культпоходы, выезды на природу, викторины и конкурсы, спортивные состязания сплачивают класс;
  • в процессе обучения ученики определяются с жизненным выбором.

Качество среднего образования в России

В эпоху СССР образование было предметом гордости советского государства. Сейчас об этом можно только вспоминать. Качество образовательного процесса сильно упало в современной России. Со времен Советского Союза в стране многое поменялось. Коснулось это и школы. Другими стали дети, ушли на пенсию педагоги старой закалки.

Ребята получили доступ к интернету, куда можно зайти со смартфона прямо на уроке. Школьники не понимают, зачем нужно «грызть гранит науки», когда есть возможность любую информацию найти в интернете. Они отказываются учить таблицу умножения. Какой в этом смысл, когда любой несложный пример можно решить с помощью калькулятора.

Изменилось и отношение учеников к педагогам. Никто уже перед ними не трепещет, как раньше. Нравы стали более свободными, а чувство ответственности у детей притупилось. Все это не лучшим образом сказалось на уровне российского среднего образования, и предложенные реформы плачевное состояние не улучшили.

Где продолжить образование после школы

Выпускникам 11 класса открыты все пути. Большинство стараются поступить в институт. Если большой уверенности в своих знаниях нет, лучше подать документы в колледж. Учиться можно как в российских ВУЗах, так и в зарубежных учебных заведениях. Одни выбирают Кембриджский или Оксфордский университет, другие — Сорбонну в Париже. Есть и другие варианты.

В последние десятилетия в России появилось много высших учебных заведений на платной основе, которые выдают своим выпускникам дипломы, которые нигде не котируются. Администрация таких академий и университетов просто собирает со студентов деньги.

Чтобы не попасть впросак, нужно предварительно собрать информацию об институте, где собирается учиться выпускник школы. Поступать необходимо только в сертифицированные ВУЗы, поскольку у псевдозаведений в любой момент могут отозвать лицензию, и диплом выпускника станет недействительным.

Гимназия

В СССР подобных заведений, бывших при царе, уже не было. Зато они стали появляться, как грибы после дождя, в условиях современной России. Сейчас уже трудно отыскать хотя бы один город в нашей стране, где гимназии отсутствуют. Статус их выше, чем у обычных школ, поэтому они и стали популярными.

История происхождения

В переводе с греческого «гимназия» означает «посещение для гимнастических упражнений». От греков данные заведения переняли в древних городах Египта и Сирии, в других странах Малой Азии, куда распространили свое влияние Греческая и Римская империи. Позднее определение упростилось до «место для упражнений».

Любые физкультурные занятия, которыми занимались мальчики, в древние времена назывались гимнастикой, будь то верховая езда, фехтование или кулачный бой.

Постепенно стали добавляться и другие дисциплины:

  • математика;
  • риторика;
  • музыка;
  • танцы;
  • гигиена.

В 16 веке средние школы для мальчиков вели обучение в Голландии, Австро-Венгрии, Германии, других европейских странах. В России гимназии появились только в 18 веке при царе-реформаторе Петре I. Первая из них открылась в 1701 году в Москве. Основал ее лютеранский пастор Эрнст Глюк.

Задачи

Цель современных заведений с петровских времен изменилась, но определенные направления остались.

Сейчас гимназия решает следующие задачи:

  1. Дает возможность широкого естественно-математического и гуманитарного обучения в формате высшей школы.
  2. Обеспечивает индивидуальное развитие личности, наклонностей, способностей и интересов учащихся.
  3. Формирует общую культуру личности на основе учебных программ.
  4. Прививает нормы общечеловеческой морали и навыки нравственного поведения.

Направленность

В начале 20 века гимназии в России имели разную направленность. Одни относились к Министерству народного просвещения, другие — к ведомству императрицы, третьи работали в частном порядке.

Среди множества заведений выделялись:

  • реальные;
  • военные;
  • коммерческие;
  • женские.

Современная гимназия, основанная на научном подходе и преемственности поколений, проповедует принципы индивидуального вектора развития, гуманизма в обучении и воспитании гимназистов.

К основным направлениям учебного процесса относятся:

  1. Изучение в совокупности художественной, материальной и духовной культуры для определения и развития у гимназистов определенных способностей.
  2. Минимум знаний (госстандарт) дает педагог, максимум, в соответствии со способностями и потребностями, определяет сам ученик.
  3. Подключение регионального компонента для привития школьникам уникальной культуры (сибирской, казанской, уральской и т. д.)
  4. Признание самоценности личности и гармонизации интересов коллектива.
  5. Приобретение навыков коммуникации и умения работать в творческой команде.

Отличие диплома

По окончании обучения гимназистам выдают точно такой же диплом, как и выпускникам СОШ. Но разница все же есть. По результатам поступления в ВУЗы формируются рейтинги гимназий. Если заведение находится в ТОП-20, статус его выпускников автоматически повышается. К таким абитуриентам в высших учебных заведениях относятся с уважением.

Есть и еще один плюс. Гимназисты имеют всестороннее образование с углубленным изучением русского языка, литературы и других школьных предметов гуманитарного направления. Обладая обширными знаниями, они без труда поступают в большинство российских вузов, что подтверждает статистика. Да и в институте им учиться легче, чем выпускникам СОШ.

Лицей

Наряду с гимназиями, в России много и не менее популярных лицеев, в которые родители с удовольствием отдают своих детей. Учеба в этом заведении тоже сопряжена с повышенными нагрузками, ведь школьникам, помимо общеобразовательной программы, нужно еще очень многое усвоить.

Когда появились лицеи

Первый лицей появился тоже в Древней Греции. Назывался он «ликей», поскольку рядом находился храм Аполлона Ликейского. Преподавали там знаменитые Аристотель и Сократ. Впоследствии в греческих лицеях обучали в основном философии. Во Франции лицеи появились только в начале 19 века по указу Наполеона. Они относились к средним учебным заведениям.

В то время лицеистов можно было встретить также в ряде стран Западной Европы, Африки, Латинской Америки. В дореволюционной России было всего 7 лицеев со сроком обучения от 6 до 11 лет. За это время учащиеся проходили программу обучения средней и высшей школы.

В основном в таких заведениях готовили будущих государственных чиновников. Самый известный из лицеев — Императорский Царскосельский, где получали знания Пушкин и Салтыков-Щедрин. Современные лицеи имеют с дореволюционными мало общего.

В большинстве своем в подобных заведениях получают среднее образование, но иногда так называют и бывшие ПТУ (профессионально-технические училища), и школы узкой специализации:

  • информационно-технологические;
  • художественно-эстетические;
  • медико-биологические;
  • юридические.

В Российской Федерации лицеи работают в тандеме с академиями, университетами, институтами. Получив диплом, лицеист поступает в «свой» ВУЗ, где для таких абитуриентов уже созданы лояльные условия.

Профессиональные направления

Как правило, лицей имеет инженерно-техническое направление. Его задача — готовить инженерные кадры для предприятий и компаний: будущих конструкторов, технологов, проектировщиков. Значительная часть заведений практикует физико-математическую специализацию.

Помимо узкоспециального, есть и другие профессиональные направления:

  • работа с одаренными и мотивированными учащимися;
  • создание индивидуальных образовательных маршрутов;
  • внедрение программ профобучения с возможностью получения в процессе обучения квалификационных категорий по профессиям;
  • укрепление сотрудничества с вузами – партнерами;
  • развитие информационных технологий в воспитательной и образовательной сферах.

С какого класса берут и как учат

В лицей поступают учащиеся, окончившие 7—8 классов средней школы. Большинство из них уже определились с выбором будущей специальности и хотят заняться углубленной подготовкой для поступления в ВУЗ. Если у ребенка крепкое здоровье и сильное желание стать в будущем высококлассным инженером, лицей для него — оптимальный вариант.

Упор в данном заведении делается на точные науки. Большое внимание уделяется математике и физике. Приоритетное значение отдается практике. Уроки ведут лучшие учителя, досконально знающие свой предмет. Часто это педагоги из ВУЗов. В процессе обучения лицеист развивается не только профессионально, но и как личность.

Особенность диплома

С дипломом лицея можно поступить сразу на второй курс технического ВУЗа. Считается, что уровень знаний лицеиста соответствует знаниям первокурсника, а иногда этот уровень и выше. Если такой возможности у института нет, абитуриенты-лицеисты поступают на общих основаниях, но условия поступления для них все равно более лояльные.

Схожие черты гимназии и лицея

Иногда данные заведения называют школами городского набора (ШГН). Они считаются более приоритетными, элитными, чем обычные средние школы.

Несмотря на принципиальные различия, гимназии и лицеи имеют много общего:

  • сохраняется основная школьная программа;
  • конкурс при приеме педагогов на работу;
  • углубленное изучение учащимися дисциплин;
  • спонсоры, обеспечивающие заведение всем необходимым;
  • диплом о среднем образовании;
  • упрощенные условия при поступлении в ВУЗ.

Лучшие заведения в России

Если посмотреть рейтинг лучших ШГН в России, то картина будет следующая. Возглавляет список СУНЦ МГУ из Москвы. На втором месте расположилась «Вторая школа» — столичный лицей. Третью строчку занял лицей научно-инженерного профиля из города Королева Московской области.

Четвертое место застолбил Президентский физико-математический лицей № 239 из Санкт-Петербурга. На пятой строчке расположился Физико-математический лицей № 31 из г. Челябинска.

Почти все остальные места достались заведениям из Москвы. Четыре строчки в рейтинге достались лицеям из города на Неве.

Из других российских городов в ТОП-30 попали:

  • лицей при ТПУ г. Томск;
  • СУНЦ НГУ г. Новосибирск;
  • Югорский физико-математический лицей-интернат г. Ханты-Мансийск;
  • Лицей №130 имени Академика М. А. Лаврентьева г. Новосибирск;
  • Мордовский республиканский лицей для одаренных детей г. Саранск;
  • Лицей №153 г. Уфа.

Видео

В этом видео девушка делится своим ученическим опытом. Она последовательно занималась в обычной школе, гимназии и лицее.

Внутри новых данных, которые предполагают, что американское образование все еще «работает на лжи» — 74

Наша кампания на конец года начинается прямо сейчас! Пожалуйста, сделайте не облагаемое налогом пожертвование в пользу The 74.

Марк Шнайдер является комиссаром Института образовательных услуг Министерства образования США. Он опубликовал следующие замечания 23 марта в IES.Ed.Gov:

Название этого блога взято из открытия книги Арне Дункана 2018 года How Schools Work . Это не было новой темой для Дункана. В 2010 году он сказал: «Как страна, мы занижаем стандарты. Мы сократили их количество из-за политического давления, и на самом деле мы лгали детям и родителям, говоря им, что они готовы, хотя на самом деле они не готовы. . . Напомним, Дункан был министром образования при президенте Обаме с 2009 года.до 2015 года — не «обычный подозреваемый» в такой убийственной критике американских школ.

В среду, 16 марта, были опубликованы последние результаты недавнего исследования стенограммы средней школы. К сожалению, они поддерживают обвинение госсекретаря Дункана в том, что школы регулярно вводят своих учеников в заблуждение. (Читайте краткое изложение Линды Джейкобсон об «академическом несоответствии» Америки прямо здесь)

Исследование стенограммы средней школы NAEP периодически собирает подробную информацию о курсах, которые посещают американские старшеклассники, включая информацию о количестве пройденных академических курсов, уровне этих курсы (например, алгебра, предварительное исчисление, исчисление) и оценки, которые выставляются учащимся. Но, пожалуй, самый важный вклад NAEP в изучение транскриптов заключается в том, что он также проводит высококачественную оценку того, что учащиеся знают и могут делать в различных областях, включая естественные науки и математику.

В только что опубликованном исследовании стенограммы средней школы есть много точек данных, которые, если бы они были истинным отражением реальности, должны были бы побудить нас всех праздновать успехи наших учеников. Вот некоторые из них:

— Выпускники средних школ получают больше кредитов, особенно по академическим предметам. Во время последнего стенограммного исследования в 2009 г. у выпускников средних школ было в среднем 27,2 единицы Карнеги. В текущем исследовании этот показатель увеличился до 28,1. Большая часть этого прироста была связана с увеличением академических курсов.

— Средний балл растет. Средний средний балл в 2019 году составил 3,11 — по сравнению с 3,00 в 2009 году.

— Выпускники проходят более строгие уровни учебной программы. NAEP использует классификационную схему для оценки общей строгости учебной программы, изучаемой учащимся, по четырем уровням — ниже стандартного, стандартному, среднему уровню и строгому — в зависимости от количества единиц Карнеги, полученных учащимся по английскому языку, математике, естественным наукам, социальным дисциплинам. исследования и языки мира. Процент учащихся, завершивших стандартную или среднюю учебную программу в 2019 г.увеличилась на 4 процентных пункта по сравнению с 2009 годом. Напротив, процент учащихся, прошедших обучение по программе ниже стандартной, снизился с 23 процентов в 2009 году до 16 процентов в 2019 году.

Больше курсов, больше строгости, больше пятерок. Все хорошо!

Но вот тут-то и приходит на ум предупреждение Дункана о лжи: несмотря на весь этот кажущийся прогресс, вот куда более мрачный итог относительно успеваемости учащихся.

— Оценки учащихся не повышаются. По сравнению с 2009 годом, баллы NAEP по естественным наукам за 2019 год не изменились, а баллы NAEP по математике за 2019 год фактически снизились для выпускников средних школ.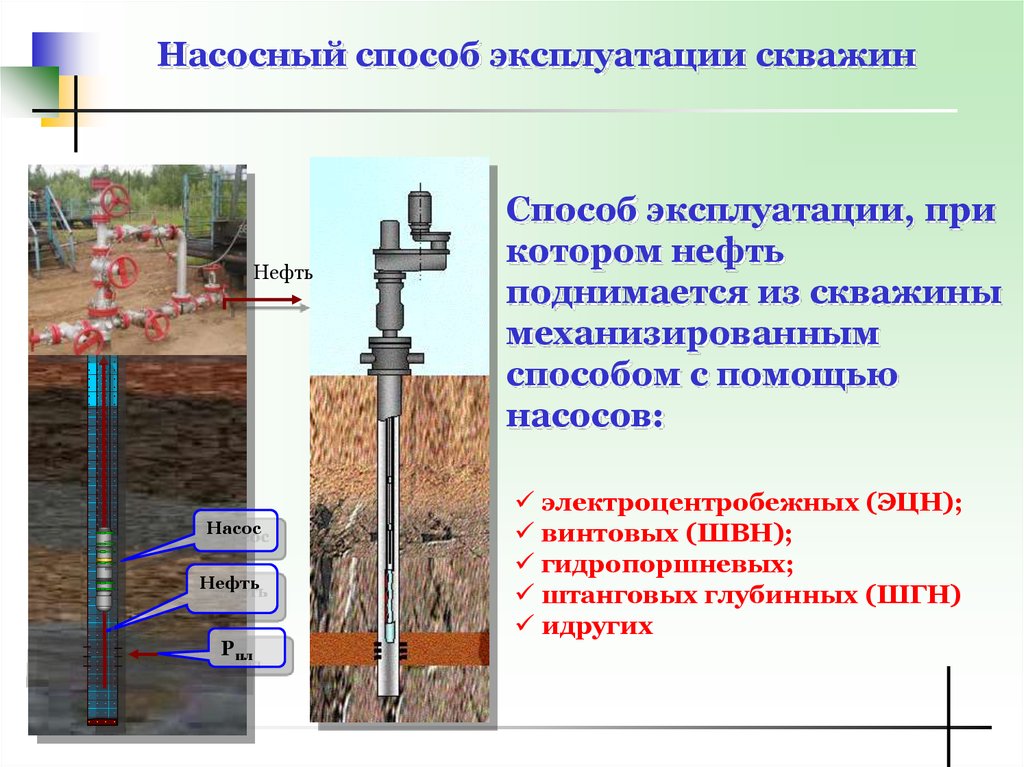

— Снижение оценок по математике у выпускников, закончивших среднюю или сложную учебную программу.

— баллы по естествознанию неизменны для всех уровней учебной программы.

— Учащиеся, завершающие наиболее распространенную учебную программу среднего уровня, набравшие в 2019 году баллы NAEP Basic как по математике, так и по естественным наукам.0003 NAEP Proficient Диапазон .

Данные из самого последнего исследования стенограмм показывают несоответствие между тем, какие курсы посещали выпускники средней школы (казалось бы, все более и более строгими), и их успеваемостью по естественным и математическим оценкам NAEP.

Мы видим «инфляцию» в оценках и названиях курсов, но стагнацию в успеваемости учащихся. NCES не проводил недавнего более подробного исследования предоставленной учебной программы, но исследование NCES 2005 года помогает объяснить это несоответствие. В этом исследовании изучалось фактическое содержание и уровень сложности курсов алгебры I и геометрии в средней школе в государственных школах по всей стране. Среди многих результатов, показывающих, что предлагаемая учебная программа часто далека от строгих названий, которые появляются в каталогах курсов, является тот факт, что только 18 процентов курсов по алгебре с отличием I и 33 процента курсов по геометрии с отличием использовали строгую учебную программу. Короче говоря, многим ученикам, даже когда им говорили, что они проходят строгую и академически ориентированную учебную программу, не давали инструментов для полного успеха в алгебре или геометрии.

Нам нужно больше учеников, изучающих математику и естественные науки. Без этого фундамента у нас никогда не будет большой, разнообразной и сильной рабочей силы STEM, что является необходимым условием для процветания экономики США. Просто сказать учащимся, которые еще не овладели навыками STEM, что они «отличники», закончившие строгую учебную программу по математике и естественным наукам, — не способ создать такую ​​рабочую силу.

Если образование построено на лжи, то это одна из самых пагубных лжи.

Как обычно, обращайтесь ко мне: [email protected]

Марк Шнайдер — директор Института педагогических наук Министерства образования США. Прежде чем занять эту должность, он был вице-президентом и научным сотрудником Американского исследовательского института, а также президентом College Measures. Ранее он занимал должность комиссара США по статистике образования с 2005 по 2008 год и является выдающимся почетным профессором политологии в Государственном университете Нью-Йорка в Стоуни-Брук.

Связанные:

Подпишитесь на информационный бюллетень The 74

Получайте подобные истории прямо на свой почтовый ящик. Подпишитесь на информационный бюллетень 74

Замечания уполномоченного – Тезисы Марка Шнайдера для региональных директоров лабораторий, Презентация стенографических исследований NCES – Резюме результатов 1982-2004

Марк Шнайдер
Уполномоченный, Национальный центр статистики образования

Выступления Марка Шнайдера перед региональными директорами лабораторий, Презентация стенографических исследований NCES – Резюме результатов 1982-2004
9 февраля 2007 г.

ВВЕДЕНИЕ
Доброе утро. Сегодня я здесь, чтобы поделиться с вами результатами исследования транскриптов, проведенного Национальным центром статистики образования.

Я рад поговорить с вами об этом, потому что исследования стенограмм, проведенные NCES, предоставили обширную информацию о курсах, которые учащиеся изучают в средней школе, их оценках, которые они получают на этих курсах, и о том, как курсы, изучаемые учащиеся относятся к своим достижениям. Эти исследования стенограмм средней школы проводились каждые 3-5 лет до 19 лет.82.

В результате они предоставляют важную информацию об изменениях в учебной программе средней школы США, и они могут предоставить вам вопросы для видов исследований, которые вы проводите, и могут предоставить национальную основу для некоторых данных, которые вы видите из школ вашего региона.

Стенограммные исследования NCES
Образование Продольное исследование второкурсников средней школы 2002 г.

  • Стенограммы, собранные у 14 900 учащихся в 2004 г.
  • Национальное исследование, в котором приняли участие 2,7 миллиона выпускников средних школ 2003–2004 годов
  • На основе стенограмм из более чем 750 государственных и частных школ
  • Включает результаты тестов учащихся по математике и чтению
  • Транскриптовые исследования также проводились в рамках лонгитюдных когорт в 1982 и 1992 гг.

Стенограмма средней школы Исследование национальной оценки образовательного прогресса

  • Национальное исследование, в котором приняли участие 2,7 миллиона выпускников средней школы 2005 года
  • Стенограммы, собранные у 26 000 учащихся в более чем 700 школах
  • Стенограммы, связанные с тестами успеваемости учащихся NAEP
  • Транскриптовые исследования, также проведенные в 1987, 1990, 1994, 1998, 2000, 2005 годах

У нас есть два основных семейства исследований транскриптов, последние волны каждого из которых были недавно проведены в этой области.

  • Семья 1: Продольные исследования средней школы Семья
    • Продольное исследование образования 2002 г. является текущей версией, и в 2009 г. мы выпустим новую версию..
    • ELS 2002 основан на выборке второкурсников средней школы в 2002 году.
    • 750 государственных и частных школ
    • ELS включает результаты тестов учащихся по математике и чтению

Сегодня я буду говорить в основном о результатах исследования транскриптов, проведенного в 2004 г. в рамках долгосрочного исследования образования 2002 г. Я буду сравнивать эти результаты с результатами исследований стенограмм, проведенных в рамках двух других долгосрочных исследований средней школы.
исследования, проведенные NCES в прошлом. Это были 1982 Компонент стенограммы средней школы и последующее обучение второкурсников 1980 года и компонент стенограммы Национального долгосрочного исследования образования 1988 года (NELS:88) 1992 года.

Каждое из этих исследований транскриптов было проведено в соответствии с общей структурой кодов курсов и методологией сбора, чтобы обеспечить сопоставимость количества кредитов по областям курса и уровням в разные годы. Эта сопоставимость позволяет анализировать тенденции прохождения курсов и их влияние на достижения, о чем я расскажу сегодня.

В презентацию я также включу некоторые результаты второго семейства транскриптов исследований, проведенных NCES в рамках Национальной оценки образовательного прогресса . Исследования транскриптов NAEP проводятся в соответствии с теми же рамками классификации курсов и методологией сбора, что и исследования транскриптов лонгитюдных исследований.

  • Семья 2: Национальная оценка образовательного прогресса
    • Исследования транскриптов NAEP проводились в 1987, 1990, 1994, 1998, 2000 и 2005 годы.
    • В 2005 году стенограммы были собраны у 26 000 учащихся из более чем 700 школ
    • Стенограммы, связанные с тестами достижений учащихся NAEP, но не так тесно, как семейство исследований ELS.
    • Данные за 2005 год будут опубликованы 22 февраля.

Имейте в виду, однако, что есть значительное количество учащихся (т. е. бросивших школу и получивших GED), которые не охвачены этими исследованиями, которые сосредоточены на выпускниках средней школы.

Также, пожалуйста, имейте в виду, что результаты, которые я буду обсуждать в презентации, включают посещение курсов в государственных и частных школах.

Теперь обратимся к выводам.

Динамика общего количества кредитов, полученных выпускниками средней школы
В период с 1982 по 2004 г.

  • Общее количество средних кредитов, заработанных выпускниками, увеличилось с 22 до 26
  • Средний кредит академических курсов увеличился
  • Средний балл по курсам профессионального образования снизился

С тех пор, как Национальная комиссия по передовым достижениям в области образования опубликовала отчет «Нация в опасности» в 1982 г., средняя общая сумма кредитов по курсам, полученным выпускниками средних школ во время их карьеры в средней школе, увеличилась с 22 кредитов в 1982 г. до 26 кредитов в 2004 г., или рост примерно на 20 процентов.

В стенограммах кредиты измеряются в единицах Карнеги – курс, который проводится каждый день, один урок в день, в течение всего учебного года.

Общее количество кредитов по академическим курсам, заработанных студентами, увеличилось больше, чем общее количество кредитов. Академические кредиты увеличились на 41 процент с 14,5 кредитов на студента в 19с 82 до 20,4 кредитов в 2004 году. Поскольку академические кредиты увеличились больше, чем общее количество кредитов, что-то должно было дать.

Что снизилось, так это профессиональное образование: в среднем с 4,5 кредитов на учащегося до 3,5 кредитов на учащегося в среднем.

Группа курсов под названием «Личное использование», которая включает личное здоровье, физическое воспитание, религию, военное дело и другие подобные предметы, увеличилась.

Динамика учебных курсов, пройденных выпускниками средней школы

  • В период с 1982 по 2004 год средний балл по курсам, пройденным выпускниками, увеличился по всем учебным предметам.

Упор на математику и естествознание в программе средней школы с 1982 года вызвал обеспокоенность у некоторых, что рост в этих и других высокоприоритетных предметных областях вытеснил курсы в других областях, таких как искусство.

Как показано на слайде, ответ, по крайней мере, для искусств таков: нет, искусство не уменьшилось по отношению к среднему общему количеству кредитов, заработанных учащимися. Искусство включает в себя изобразительное и исполнительское искусство: изобразительное искусство, музыку, танцы, дизайн, ремесла и так далее. Средние кредиты в искусстве увеличились на 8 процентов между 1998 и 2004. За тот же период средние кредиты, полученные студентами по математике и естественным наукам, увеличились на 8 и 7 процентов соответственно. За последние два десятилетия темпы роста искусства в искусстве были примерно такими же, как в математике и естественных науках. В период с 1982 по 2004 год средние баллы по искусству увеличились на 40 процентов. По математике и естественным наукам рост составил 40 и 52 процента соответственно.

Динамика среднего количества баллов по граждановедению и искусству, полученных выпускниками
На этом слайде мы можем ясно видеть рост искусства с правой стороны. Процент увеличения довольно высок, но, конечно, он находится на низком уровне.

Другим предметом беспокойства были гражданские права. В столбцах слева от вас мы видим, что в период с 1982 по 1998 год в курсе по граждановедению произошли большие скачки, а с тех пор — небольшой спад.

«Гражданское право» включает курсы по федеральному управлению и управлению штатами, конституции, выборам, сравнительному политическому регулированию, политологии и другим областям.

Тенденции в прохождении курсов математики и естественных наук продвинутого уровня

  • Процент учащихся, достигших продвинутого уровня математики и естественных наук , курсовая работа значительно увеличилась с 1982 года

На этом слайде показаны тенденции в завершении курса математики и естественных наук по наивысшему академическому уровню математики и естественных наук, который завершают учащиеся. Эти уровни определяются в соответствии с последовательностью курсов, предписывающих изучение этих областей: например, алгебра I обычно завершается перед алгеброй II, а алгебра II — перед тригонометрией и исчислением.

NCES разделил математику и естественные науки на средний и продвинутый уровни курсовой работы, а затем, в каждой из этих областей, на последовательности курсов, которые обычно завершаются. Подобные конвейеры также были разработаны для английского и иностранных языков.

Важно повторить, что академический уровень курсов, пройденных учащимися, измеряется пройденным курсом самого высокого уровня, а не количеством кредитов, заработанных на каждом уровне.

Здесь мы видим, что число учащихся, достигших уровня Advanced, увеличилось примерно с одной четверти (разница между показанным общим числом и «средним уровнем» Алгебры 2) примерно до половины в 2004 году. Помните, что это основано на пройденном курсе. а не по результатам достижений. В науке процент на продвинутом уровне удвоился между 1992 и 2004.

Тенденции в учебной программе, пройденной выпускниками средних школ

  • Шестьдесят процентов всех выпускников средних школ выполнили требования стандарта «Новые основы» или строгой учебной программы в 2004 г.
  • Около 20 процентов выпускников выполнили эти требования в 1982 году

Учебная программа «Новые основы», первоначально обнародованная Комиссией по совершенствованию в 1982 году, установила стандарт в 4 кредита по английскому языку и по 3 кредита по математике, естественным наукам и общественным наукам в качестве стандарта для окончания средней школы по основным академическим предметам.

Уровнем выше, чем эта «Стандартная» учебная программа по новым основам, является Строгая учебная программа , которая требует завершения той же комбинации из 4 кредитов по английскому языку и 3 кредитов по математике, естественным наукам и общественным наукам, а также по крайней мере один из кредиты по математике и хотя бы один по естественным наукам должны быть на продвинутом уровне.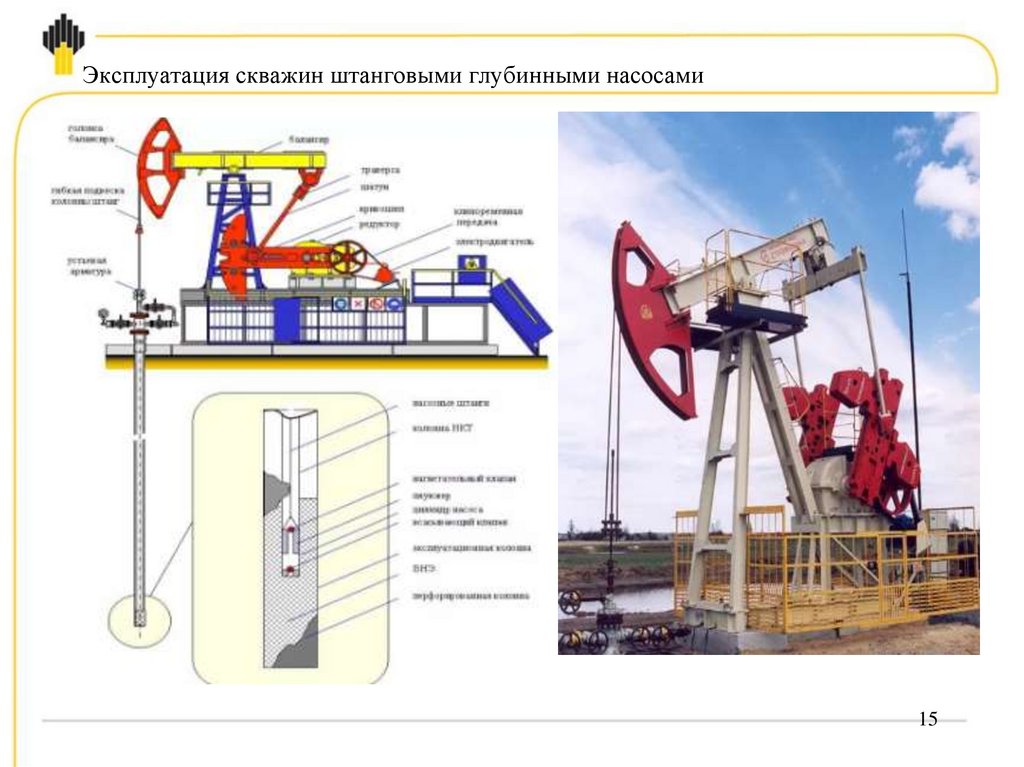 Кроме того, студент должен иметь как минимум 2 кредита по иностранному языку на одном языке.

Процент учащихся, завершивших стандартную учебную программу, вырос с 14 процентов в 19с 82 до 25 процентов в 1992 году и до 32 процентов в 2004 году. Доля учащихся, прошедших строгую учебную программу, увеличилась с 6 процентов в 1982 году до 28 процентов в 2004 году.

Поскольку строгая учебная программа основана на получении кредитов на курсах математики, естественных наук и иностранных языков продвинутого уровня, она позволяет измерить процент учащихся, достигших продвинутого уровня по всем трем этим предметам. В отличие от двух третей учащихся, достигших продвинутого уровня по естественным наукам, и половины учащихся, достигших продвинутого уровня по математике в 2004 г., в целом только 28 процентов прошли строгий учебный план.

Законченные курсы математики в девятом и, возможно, в 12-м классах

  • Среди учащихся, изучающих геометрию в 9-м классе, 84 процента заканчивают тригонометрию/предварительное исчисление или исчисление к 12-му классу
  • Среди учащихся, изучающих курсы ниже алгебры I в 9-м классе, только 10 процентов заканчивают тригонометрию/предварительное исчисление или исчисление к 12-му классу

Стенограммы также можно использовать для изучения пути, которым учащиеся следуют в старшей школе, и того, как выбор в начале старшей школы влияет на них позже.

Иерархия курсов, пожалуй, является наиболее структурированной по математике среди всех академических предметов средней школы. Из-за этого курсы, которые учащиеся изучают в 9-м классе, определяют академический уровень математики, который они могут пройти к 12-му классу.

Среди учащихся, изучающих геометрию в 9-м классе, 84 процента достигают продвинутого уровня математики, что в качестве переподготовки означает прохождение хотя бы одного курса по тригонометрии, аналитической геометрии, предварительному исчислению или исчислению.

Среди учащихся, изучающих общую или прикладную математику в 9-м классе, 35 процентов не осваивают дальше алгебры I или геометрии и только 10 процентов доходят до продвинутого уровня — тригонометрии, планиметрии, предварительного исчисления или исчисления.

Среди тех, кто изучает алгебру I в 9-м классе, только 46 процентов достигают уровня Advanced. Отсутствие алгебры I в 8-м классе является реальным препятствием для достижения продвинутого уровня по математике.

Курс математики, изучаемый в 9й класс
В период с 1982 по 2004 год процент девятиклассников, завершивших:

  • Общая или базовая прикладная математика снизилась с 27 до 7 процентов
  • Алгебра I увеличилась с 44 до 51 процента
  • Геометрия увеличена с 5 до 18 процентов

Тогда возникает вопрос, каково распределение курсов математики, которые учащиеся изучают в 9-м классе, и меняется ли это распределение курсов со временем?

Как показано во второй слева группе элементов на диаграмме, процент учащихся, изучающих общую или прикладную математику в 9-м классе, снизился с 27 процентов в 1982 году до примерно 7 процентов сегодня. Как показано в середине диаграммы, процент учащихся, завершивших алгебру I в 9-м классе, вырос с 44 до 51 процента. Как показано справа, процент учащихся, завершающих геометрию в 9-м классе, вырос с 5 до 18 процентов.

Все больше учеников вступают на путь более строгой математики.

Курсы повышения квалификации и успеваемость, 2004 г.

  • Выпускники, окончившие курсы повышения квалификации по математике, в 2004 г. имели более высокие баллы успеваемости, чем другие учащиеся

Последствия прохождения курсов математики продвинутого уровня для достижений выпускников можно измерить с помощью тестов, являющихся частью опроса ELS:2002.

В тесте ELS:2002 используется теория ответных заданий (IRT), в которой используются шаблоны правильных, неправильных и пропущенных ответов для получения оценок способностей, сопоставимых по широкому диапазону тестовых форм и успеваемости учащихся. Тест является полуадаптивным в том смысле, что учащиеся с разным уровнем успеваемости получают разные формы теста.

При оценке способностей учащегося IRT также учитывает сложность каждого тестового вопроса, способность к различению по сравнению с другими элементами и фактор угадывания, где последний важен для точного тестирования низких достижений.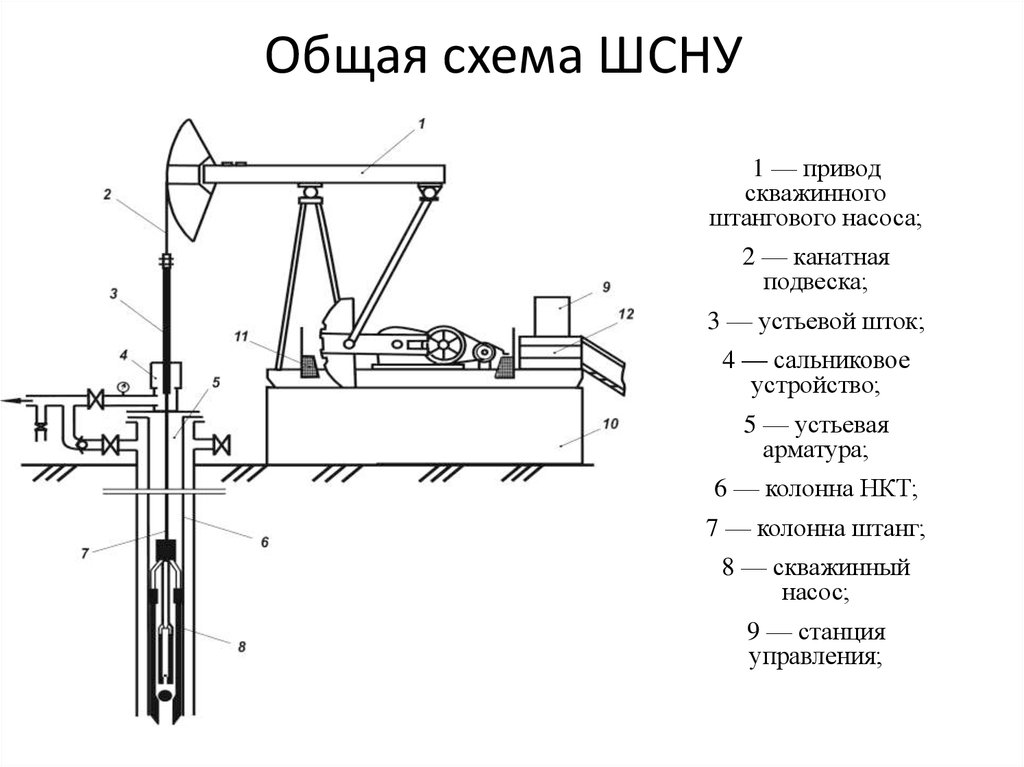 Элементы для тестов ELS: 2002 были адаптированы из основ, используемых для NELS:88, чтобы можно было сравнивать результаты этих тестов.

Взаимосвязь между курсами математики самого высокого уровня, пройденными выпускником, и проверенным уровнем успеваемости выпускника, четко показана на слайде. Выпускники средних школ, получившие более высокий уровень знаний по математике, имеют более высокие математические достижения по результатам тестов ELS:2002.

Курсы продвинутого уровня и успеваемость, 1992 и 2004 годы

  • Рост оценок по математике статистически не отличался в 1992 и 2004 годах.

На этом слайде показана взаимосвязь между курсами высшей математики, пройденными выпускниками средних школ в 1992 г., и их проверенными достижениями в исследовании NELS:88 Transcript вместе с результатами ELS за 2004 г. Статистические тесты показывают, что рост успеваемости на всех уровнях Прохождение курса существенно не отличается для NELS в 19 лет. 92 и ELS в 2004 г.

Можно подумать, что прирост успеваемости в результате прохождения курсов математики более высокого уровня продвинутого уровня может быть меньше в 2004 г., чем в 1992 г., из-за увеличения процента учащихся, которые в настоящее время достигают продвинутого уровня знаний. математика в средней школе. Это увеличение вполне могло привести к уменьшению взаимосвязи между прохождением курса и успеваемостью, так как все больше студентов, которые в предыдущие годы не занимались углубленной курсовой работой, теперь ее проходят. В рамках этого простого сравнительного анализа такая «снижающаяся» предельная отдача от увеличения количества занятий по математике не очевидна.

Различия в уровне прохождения курсов в зависимости от пола

  • В 1982 году женщины реже, чем мужчины, заканчивали математические курсы продвинутого уровня

Можно также сравнить завершение курса математики и успеваемость между различными группами населения.

Один из важных вопросов касается прогресса женщин в математике и естественных науках. Давайте сосредоточимся на математике, потому что это предмет, который мы довольно подробно обсуждали сегодня.

В 1982 году у женщин было меньше шансов достичь продвинутого уровня математики, чем у мужчин, хотя не многие мужчины или женщины достигли этого. Разница составила 25-28 процентов или -3 процента.

К 2004 году пропорции мужчин и женщин, достигших продвинутого уровня математики, увеличились до такой степени, что доля женщин, достигших продвинутого уровня математики , превысила долю мужчин, достигших этого уровня, что было заметным изменением по сравнению с ситуацией. в 1982 году. Разница была 53 на 49процентов, или +4 процента.

Различия в успеваемости в зависимости от уровня прохождения курса и пола

  • У мужчин были более высокие результаты по математике, чем у женщин, окончивших математические курсы того же уровня в 2004 году.

Это преимущество в завершении курса по сравнению с мужчинами, однако, не привело к более высоким математическим достижениям, чем у мужчин по уровню курса в 2004 году, как показано на этом слайде. В 2004 г. у мужчин были более высокие оценки успеваемости по математике, чем у женщин, на всех уровнях математических курсов, за исключением нулевой/низкой математики.

Различия в уровне прохождения курсов в зависимости от расы/этнической принадлежности

  • Доля белых и чернокожих, достигших продвинутого уровня математики, выросла в период с 1982 по 2004 год.

Такой же вопрос можно задать о различиях в академическом уровне математики, достигнутом в старшей школе, и успеваемости по расе/этнической принадлежности.

Доля белых и чернокожих, достигших продвинутого уровня математики, выросла с 1982, но доля чернокожих, делающих это, остается ниже доли белых. Измеряемый как абсолютная разница в этих пропорциях между черными и белыми, разрыв в 1982 году статистически не отличается от разрыва в 2004 году. Латиноамериканцы, достигшие продвинутого уровня математики, выросли в период с 1982 по 2004 год.

Результат одинаков для белых и латиноамериканцев. Доля как белых, так и латиноамериканцев, достигших продвинутого уровня математики, выросла между 1982 и 2004, но доля латиноамериканцев остается ниже доли белых. Измеряемый как абсолютная разница в долях латиноамериканцев и белых, достигших продвинутого уровня, разрыв в 1982 г. статистически не отличается от 2004 г.
Доля как белых, так и азиатов, достигших продвинутого уровня математики, выросла в период с 1982 по 2004 год.82. Доля обеих групп, достигших продвинутого уровня, выросла в период с 1982 по 2004 год, и в 2004 году доля азиатов, достигших продвинутого уровня математики, оставалась выше, чем доля белых.

Различия в уровне прохождения курса в зависимости от расы/этнической принадлежности

  • Доля белых и коренных американцев, достигших продвинутого уровня математики, выросла в период с 1982 по 2004 год.

Тенденции в пропорциях белых и коренных американцев, достигших продвинутого уровня математики, аналогичны пропорциям белых, чернокожих и выходцев из Латинской Америки. Доля как белых, так и коренных американцев, достигших продвинутого уровня, выросла между 1982 и 2004. Однако, в отличие от моделей для белых, чернокожих и латиноамериканцев, разрыв между белыми и коренными американцами в прохождении курсов продвинутого уровня вырос на между 1982 и 2004 годами.

раса/этническая принадлежность

  • Белые получили более высокие средние баллы по математике, чем чернокожие и латиноамериканцы, закончившие курс математики того же уровня в 2004 г.
  • Достижения азиатских выпускников существенно не отличались от достижений белых, окончивших курсы математики того же уровня в 2004 г.

Картина различий в успеваемости по математике по уровням курса аналогична для белых по сравнению с чернокожими и для белых по сравнению с латиноамериканцами. Достижения чернокожих меньше, чем у белых на всех уровнях курса выше нулевой или низкой математики, как и достижения латиноамериканцев.

Картина для азиатов и белых разная. Достижения азиатов ненамного выше, чем у белых, на каком-либо конкретном уровне математики, но выше, если усреднить их по всем уровням. Причиной этого является больший процент азиатов, чем белых, достигших высшей математики. Этот результат, который может удивить некоторых, является следствием сравнения достижений по уровням курса. Например, в исчислении нет разницы в достижениях между белыми и азиатами. Если бы азиаты не достигали продвинутого уровня прохождения курсов намного чаще, чем белые, их успеваемость по математике в среднем не была бы выше, чем у белых.

Долгосрочные тенденции в успеваемости по математике

  • Успеваемость по математике в 2004 г. была выше, чем в 1982 г. и двух других годах

Ранее в этой презентации я отмечал связь между более частым знакомством с курсовой работой продвинутого уровня и достижениями — по крайней мере, в математике. Если это так, то можно разумно ожидать, что средний уровень успеваемости учащихся в целом должен был повыситься в период, когда произошло расширение курсовой работы продвинутого уровня в школьной программе. Это случилось?

В Оценке долгосрочных тенденций Национальной оценки прогресса в области образования NCES измерил достижения в области математики в действительно долгосрочной перспективе — с 1973 года до самых последних результатов в 2004 году.

Эта оценка отличается от » основной NAEP», также известный как Nation’s Report Cards, о котором вы читали в газетах.

Долгосрочные тенденции были продолжены NCES именно потому, что они предназначены для измерения долгосрочных тенденций в достижениях, для которых Национальный табель успеваемости изначально не предназначался.

Что показывает оценка долгосрочной тенденции?

Как видно из данных, отмеченных звездочками на экране, это показывает, что успеваемость по математике в 2004 г. была выше, чем в 1982 и 1986 гг. , когда первоначально была разработана учебная программа «Новые основы».

Но насколько выше? Ответ заключается в том, что сейчас он на 10 пунктов выше, чем был тогда, что составляет примерно одну треть стандартного отклонения за более чем 20 лет.

Мы наблюдали повышение строгости при изучении предметов в старшей школе и повышение результатов по математике в долгосрочной программе NAEP — корреляция существует, но очевидно, что ее нельзя интерпретировать как причинно-следственную связь. Только другие виды исследований могут в конечном счете напрямую связать изменения в учебной программе с изменениями в успеваемости и другими показателями успеха.

Долгосрочные тенденции в успеваемости по чтению

  • Успеваемость по чтению в 2004 г. была ниже, чем в период с 1984 по 1992 г.

Как насчет чтения? На этом слайде показано, что показатели чтения увеличились с 1971 года и достигли своего пика в начале 1990-х годов.