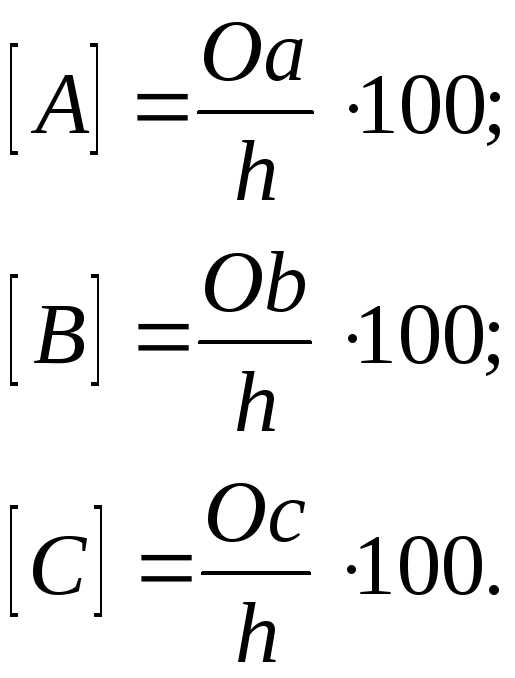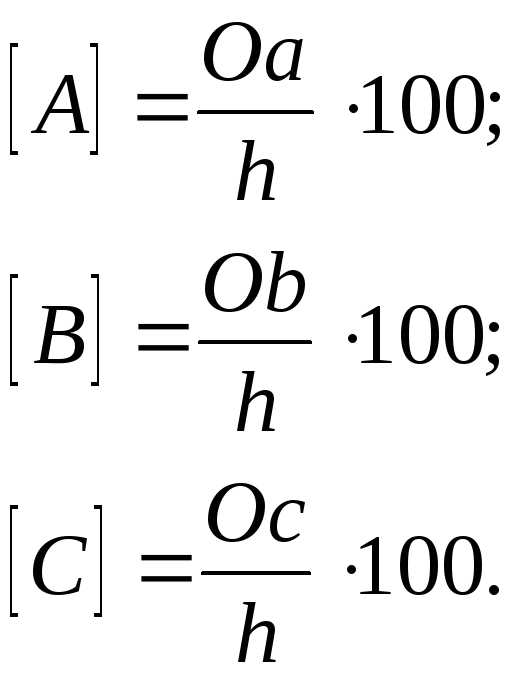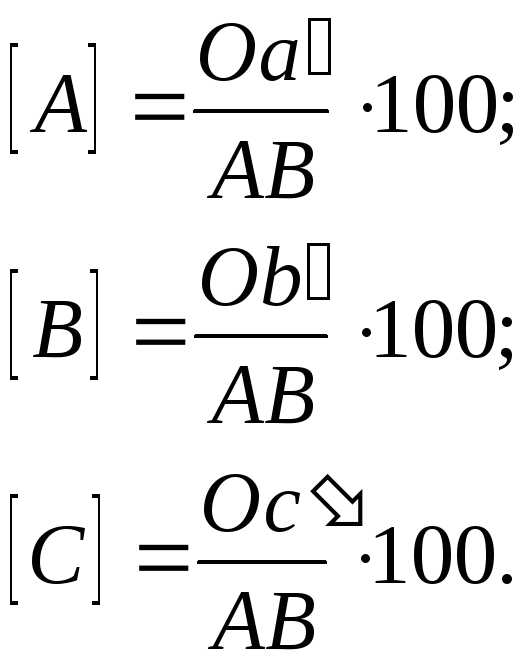Глава 9 трЕхкомпонентные системы. Трехкомпонентные системы
Глава 10. Трехкомпонентные системы
10.1. Способы изображения состава трехкомпонентных систем
Для построения полной диаграммы состояния трехкомпонентной системы необходима система координат из пяти взаимно перпендикулярных осей, по которым откладываются температура, давление, мольные объемы различных фаз и мольные доли (или массовые проценты) двух компонентов в фазах. Реально построение такой диаграммы невозможно. Нельзя также построить проекцию этой диаграммы на четырехмерное пространство в осях: температура, давление, мольные доли двух компонентов. Лишь приняв какой-либо из параметров, например, температуру или давление, постоянным, можно построить трехмерную диаграмму, которая будет отображать зависимость числа и состава фаз в равновесных системах от исходного состава и от температуры (при постоянном давлении) или от давления (при постоянной температуре).
Часто для еще большего упрощения постоянными принимаются температура и давление одновременно. В этом случае на плоскости составов наносятся проекции сечения трехмерной диаграммы плоскостью T= const илиp= const. Двумерные диаграммы отражают различные состояния системы и фазовые переходы только при выбранных значенияхpиT.
При построении диаграммы состояния трехкомпонентной системы состав ее изображают на плоскости, а в перпендикулярном направлении откладывают температуру (p= const) или давление (T= const). Чаще используется первый вариант, так как давление в большинстве случаев при изучаемых превращениях остается постоянным или изменяется немного, а температурные изменения значительны.
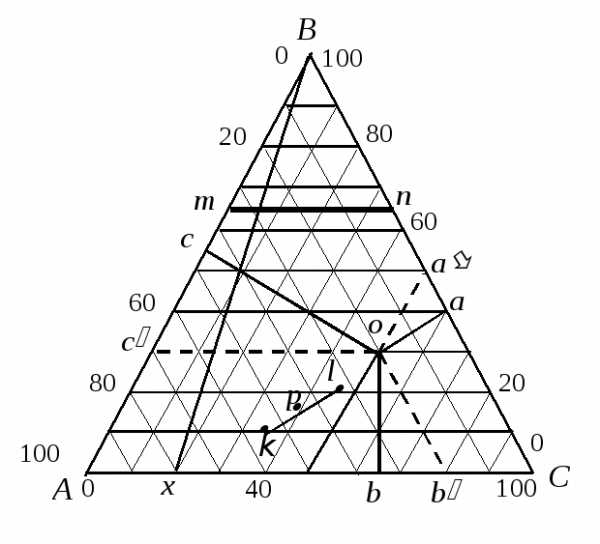
Рис.10.1. Треугольник Гиббса – Розебома для изображения состава трехкомпонентной системы
Состав трехкомпонентной системы обычно изображают, пользуясьтреугольником Гиббса – Розебома(рис. 10.1). Вершины равностороннего треугольника отвечают чистым компонентам (100%) A, B и C. Каждая из сторон треугольника позволяет описать составы двухкомпонентных систем A + B, B + C, A + C. Все точки внутри треугольника описывают составы трехкомпонентных систем.Метод определения состава по Гиббсу основан на том, что сумма перпендикуляров, опущенных из любой точки равностореннего треугольника на каждую из сторон, равна высоте треугольника. Если принять, что высота треугольника соответствует 100 мольным (или массовым) процентам, то состав тройной системы можно выразить с помощью длин перпендикуляров. При этом содержанию данного компонента отвечает длина перпендикуляра, опущенного на сторону, противоположную соответствующей вершине треугольника. Например, точка оотвечает составу: 20% компонента A (отрезокоа), 30% компонента B (отрезокоb) и 50% компонента C (отрезокоc).
Длина перпендикуляра оценивается с помощью координатной сетки, покрывающей треугольник. Высоты треугольника делятся на 10 или 100 равных отрезков и через точки деления проводятся три группы параллельных прямых так, что каждая группа перпендикулярна соответствующей высоте треугольника, при этом длина каждого получающегося отрезка отвечает 10 или 1% содержания данного компонента в смеси.
Выражение составов трехкомпонентных систем по Розебому основано на том, что сумма отрезков, проведенных из какой-либо точки внутри треугольника параллельно его сторонам до пересечения с каждой из сторон, равна длине стороны треугольника. Координатная сетка образована тремя группами прямых, параллельных сторонам треугольника. Содержанию каждого компонента отвечает длина отрезка, проведенного к стороне, лежащей против вершины этого компонента. На рис. 10.1 эти отрезки нанесены пунктиром; длины отрезков oa,obіocсоответствуют содержаниям компонентов A, B, C.
Линии, параллельные одной из сторон треугольника, представляют геометрические места точек, соответствующих смесям с одинаковым содержанием одного из компонентов. Например, линия mnотвечает смесям, в которых содержание компонента B составляет 65%.
Линии, проведенные из вершин треугольника до пересечения с противолежащей стороной, являются геометрическими местами точек, соответствующих ряду систем, в которых соотношение между содержанием двух компонентов остается постоянным. Так, например, линия Bхотвечает ряду смесей, в которых процентное содержание A и C сохраняется равным 8:2.
К треугольной диаграмме, как и диаграмме бинарных систем, приложимо правило рычага. Если, например, точка ротвечает общему составу системы, а система распадается на две фазы составовkиl, то количество первой фазы относится к количеству второй как длины отрезковpl :pk.
Составы трехкомпонентных систем иногда изображают в прямоугольных координатах, что значительно упрощает расчеты количеств отдельных фаз. Этот способ чаще всего применяют для изображения состава растворов двух солей с общим ионом. Для построения прямоугольной диаграммы состав системы выражают не в мольных или массовых процентах, а числом молей или граммов каждой соли, приходящихся на 100 молей или 100 граммов воды (или другое постоянное количество). При этом на оси абсцисс откладывают содержание одной соли, а на оси ординат – содержание другой. Начало координат соответствует чистому растворителю.
studfiles.net
Трехкомпонентные системы
Правила фаз Гиббса для трехкомпонентных систем (КН = 3), если на систему действуют два переменных фактора (давление и температура), выражаются уравнением:
Это означает, что максимально могут существовать пять равновесных фаз только при определенном составе всех компонентов и конкретных температуре и давлении (при этом система будет безвариантной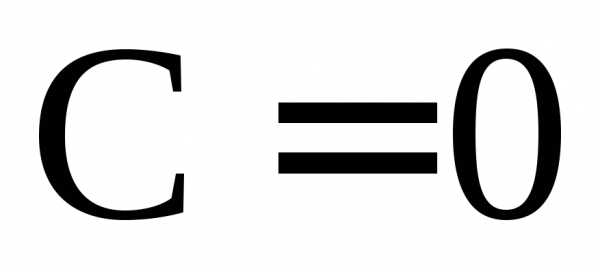 
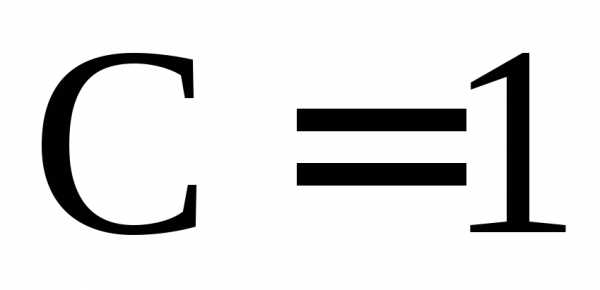). Максимальное число степеней свободы в таких системах равно четырем (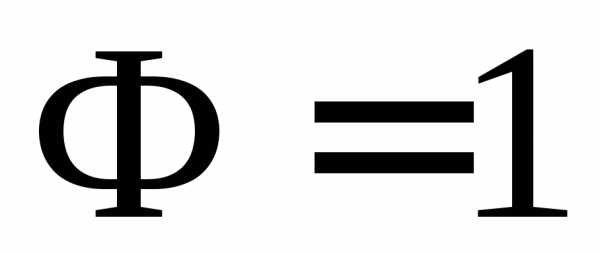
, 
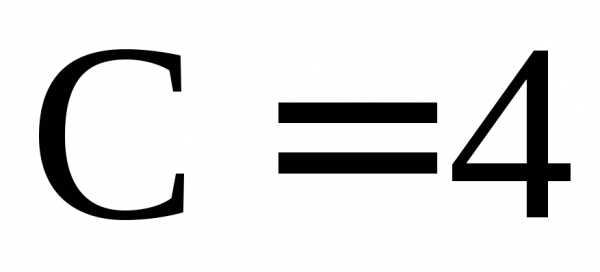), т.е. независимыми параметрами могут быть давление, температура, концентрации двух компонентов, выраженных в мольных долях. В этом случае полная диаграмма, в которой четыре переменных (Р, Т, Х1, Х2) должна быть четырехмерной.
Если же рассматривать конденсированные трехкомпонентные системы (жидкие или твердые) при постоянном давлении (Р-const, то диаграмма такой системы представляется в виде трехмерной призмы, основанием которой служит равносторонний треугольник состава, а по высоте откладывается температура.
При Р-const
. (6)
Изучение равновесий в трехкомпонентной системе еще более упрощается при постоянных давлении и температуре (Р, Т-const).
Тогда
. (7)
Степень свободы (или вариантов системы), рассчитанная по уравнению (6) и (7), называется условной (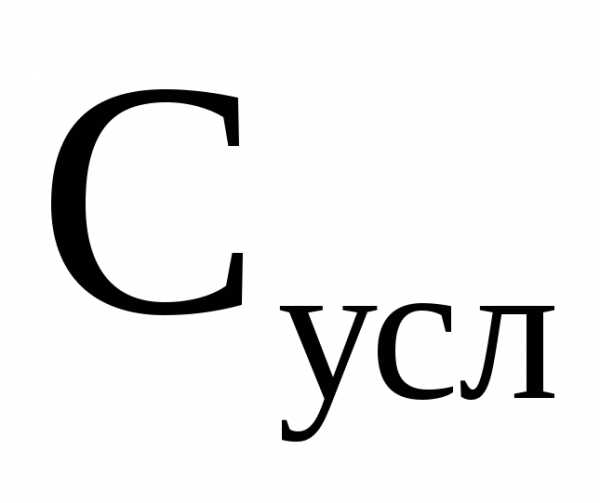
), а система – условно инвариантной (
), условно моновариантной (
) и т.д.
Если рассматривать равновесие в таких системах при Р, Т-const, то диаграмма может быть представлена в виде равностороннего треугольника состава. В таком треугольнике точки, находящиеся на его сторонах, отвечают составам соответствующих бинарных систем, выраженных в долях (молярных или массовых).
Для удобства расчета состава системы по таким диаграммам стороны треугольника делят на 100 (или 10) частей и через точки деления проводят прямые, параллельные соответствующим сторонам.
Состав системы (соотношение между содержанием компонентов) можно определить двумя методами: метод Гиббса и метод Розебума. Оба метода приводят к одинаковым результатам.
Метод Гиббса
Соотношение между компонентами по методу Гиббса определяется на основании свойства равностороннего треугольника.
| Сумма длин перпендикуляров, опущенных из любой точки внутри равностороннего треугольника на его стороны, равна его высоте, которая принимается за 1 или за 100%. |
Пример. Определить содержание веществ А, В и С в точке D (рис. 11).
Решение.
Из точки D опускаем перпендикуляр на стороны (DM, DN, DF). Замеряем их длину (определяем размеры).
DM = 37 мм,
DN = 30 мм,
DF = 20 мм.
Их общая длина равна длине высоты треугольника CE.
–принимаем за 100%.
Расчет.
1. Содержание компонента А определяется длиной перпендикуляра DM:
87 – 100%
37 – х %
в точке D содержится 42,5% компонента А.
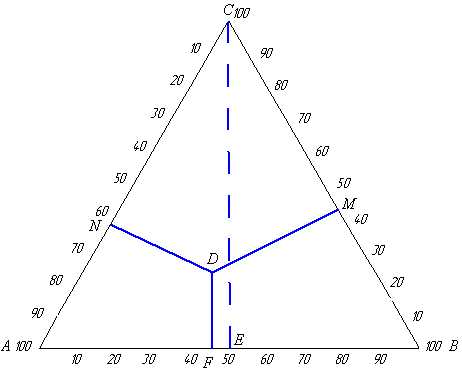
Рис. 11. Определение состава трехкомпонентной системы
по методу Гиббса
2. Содержание компонента В определяется длиной перпендикуляра DN:
87 – 100%
30 – х %
в точке D содержится 34,5% компонента В.
3. Содержание компонента С определяется длиной перпендикуляра DF:
87 – 100%
20 – х %
в точке D содержится 23% компонента C.
studfiles.net
Глава 9 трЕхкомпонентные системы
§ 9.1. Применение правила фаз Гиббса к
Трехкомпонентным системам
Для трехкомпонентной системы, на равновесие в которой из внешних факторов оказывают влияние только давление и температура, правило фаз Гиббса выражается уравнением
| |
Отсюда следует, что в трехкомпонентной системе число фаз, находящихся в равновесии, не может быть больше пяти (С = 0, еслиФ = 5), а максимальное число термодинамических степеней свободы, т.е. независимых параметров состояния системы, равно четырём – давление, температура и концентрацииХ1иХ2двух компонентов,выраженные в массовых или молярных долях или процентах (С = 4, еслиФ = 1). При выбранных параметрах состояния системы (Р,Т,Х1,Х2) полная диаграмма состояния должна быть четырехмерной. В связи с этим состояние трехкомпонентной системы и равновесие фаз в ней рассматривают при постоянном давлении и строят трехмерную пространственную диаграмму состояния в виде прямой трехгранной призмы, основанием которой служит равносторонний треугольник состава, а по высоте откладывается температура. При P = const
| (9.2) |
Изучение равновесий в трехкомпонентной системе еще более упрощается при постоянных давлении и температуре. В этом случае можно использовать плоскую диаграмму состояния, являющуюся сечением трехгранной призмы, параллельным основанию (диаграмма состава). При P = const или T = const
| (9.3) |
§ 9.2. Графическое изображение состава трехкомпонентных систем
Для графического изображения состава трехкомпонентных систем при постоянных РиТприменяются треугольные и прямоугольные диаграммы. Треугольные диаграммы строят по методу Гиббса или по методу Розебума. В каждом из этих методов используется равносторонний треугольник (рис. 9.1.), вершины которого соответствуют чистым компонентамА,В, иС. Фигуративная точка, лежащая на любой из сторон треугольника, изображает состав соответствующей двухкомпонентной системы, а фигуративная точка, находящаяся внутри этого треугольника, – состав состав трехкомпонентной системы.
Определение состава системы при помощи треугольника концентраций можно провести двумя методами: методом Гиббса и методом Розебома.
Метод Гиббса заключается в том, что из данной точки (например, точки О) проводятся перпендикуляры на каждую из сторон. Сумма длин этих перпендикуляров равна высоте треугольникаh, которую принимают за 100 %. Тогда состав трёхкомпонентной системы можно выразить в объёмных процентах с помощью длин перпендикуляров. При этом длина каждого перпендикуляра, опущенного на данную сторону пропорциональна содержанию компонента, отвечающего вершине, лежащей против данной стороны. Например, в т.О:
|
| (9.4) |
По методу Розебома из данной точки проводятся отрезки, параллельные сторонам треугольника. Сумма этих отрезков равна стороне треугольника, которая принимается за 100 %. Длина каждого отрезка, проведённого к данной стороне, отвечает содержанию компонента, находящегося в вершине, противоположной этой стороне. Например, в точке О:
| (9.5) |
Наиболее удобным для практического использования является разновидность метода Розебома. В этом случае из точки «О» проводят две прямые, параллельные двум сторонам треугольника до пересечения с третьей. При этом третья сторона разбивается на отрезки соответствующие содержанию всех трёх компонентов (рис. 9.1). Методы Гиббса и Розебома приводят к одинаковому результату, так как стороны и высоты равностороннего треугольника пропорциональны друг другу.
Треугольная диаграмма имеет несколько важных свойств.
1. Точки, лежащие на прямой, проходящей через одну из вершин треугольника и пересекающей противолежащую ей сторону (рис. 9.2), отображают системы с постоянным соотношением концентраций двух компонентов, через вершины которых прямая не проходит. Это следует из пропорциональности длин перпендикуляров, опущенных из любой точки указанной прямой на соответствующие стороны.Так точкиb1иb2, лежащие на прямойBb, проходящей через вершинуB, отображают системы с постоянным соотношением концентраций компонентовAиC.
2. Точки, лежащие на прямой, проходящей через две стороны, параллельно третьей (рис. 9.2), отображают системы с постоянным содержанием компонента, которому эта вершина отвечает. Например, в любой точке на линии OO1, содержание компонентаBодинаково (Ob3 = O1b4).
studfiles.net
Глава 9 трЕхкомпонентные системы
§ 9.1. Применение правила фаз Гиббса к
Трехкомпонентным системам
Для трехкомпонентной системы, на равновесие в которой из внешних факторов оказывают влияние только давление и температура, правило фаз Гиббса выражается уравнением
| (9.1) |
Отсюда следует, что в трехкомпонентной системе число фаз, находящихся в равновесии, не может быть больше пяти (С = 0, еслиФ = 5), а максимальное число термодинамических степеней свободы, т.е. независимых параметров состояния системы, равно четырём – давление, температура и концентрацииХ1иХ2двух компонентов,выраженные в массовых или молярных долях или процентах (С = 4, еслиФ = 1). При выбранных параметрах состояния системы (Р,Т,Х1,Х2) полная диаграмма состояния должна быть четырехмерной. В связи с этим состояние трехкомпонентной системы и равновесие фаз в ней рассматривают при постоянном давлении и строят трехмерную пространственную диаграмму состояния в виде прямой трехгранной призмы, основанием которой служит равносторонний треугольник состава, а по высоте откладывается температура. При P = const
| (9.2) |
Изучение равновесий в трехкомпонентной системе еще более упрощается при постоянных давлении и температуре. В этом случае можно использовать плоскую диаграмму состояния, являющуюся сечением трехгранной призмы, параллельным основанию (диаграмма состава). При P = constилиT = const
| (9.3) |
§ 9.2. Графическое изображение состава трехкомпонентных систем
Для графического изображения состава трехкомпонентных систем при постоянных РиТприменяются треугольные и прямоугольные диаграммы. Треугольные диаграммы строят по методу Гиббса или по методу Розебума. В каждом из этих методов используется равносторонний треугольник (рис. 9.1.), вершины которого соответствуют чистым компонентамА,В, иС. Фигуративная точка, лежащая на любой из сторон треугольника, изображает состав соответствующей двухкомпонентной системы, а фигуративная точка, находящаяся внутри этого треугольника, – состав состав трехкомпонентной системы.
Определение состава системы при помощи треугольника концентраций можно провести двумя методами: методом Гиббса и методом Розебома.
Метод Гиббса заключается в том, что из данной точки (например, точки О) проводятся перпендикуляры на каждую из сторон. Сумма длин этих перпендикуляров равна высоте треугольникаh, которую принимают за 100 %. Тогда состав трёхкомпонентной системы можно выразить в объёмных процентах с помощью длин перпендикуляров. При этом длина каждого перпендикуляра, опущенного на данную сторону пропорциональна содержанию компонента, отвечающего вершине, лежащей против данной стороны. Например, в т.О:
|
| (9.4) |
По методу Розебома из данной точки проводятся отрезки, параллельные сторонам треугольника. Сумма этих отрезков равна стороне треугольника, которая принимается за 100 %. Длина каждого отрезка, проведённого к данной стороне, отвечает содержанию компонента, находящегося в вершине, противоположной этой стороне. Например, в точке О:
|
| (9.5) |
Наиболее удобным для практического использования является разновидность метода Розебома. В этом случае из точки «О» проводят две прямые, параллельные двум сторонам треугольника до пересечения с третьей. При этом третья сторона разбивается на отрезки соответствующие содержанию всех трёх компонентов (рис. 9.1). Методы Гиббса и Розебома приводят к одинаковому результату, так как стороны и высоты равностороннего треугольника пропорциональны друг другу.
Треугольная диаграмма имеет несколько важных свойств.
1. Точки, лежащие на прямой, проходящей через одну из вершин треугольника и пересекающей противолежащую ей сторону (рис. 9.2), отображают системы с постоянным соотношением концентраций двух компонентов, через вершины которых прямая не проходит. Это следует из пропорциональности длин перпендикуляров, опущенных из любой точки указанной прямой на соответствующие стороны.Так точкиb1иb2, лежащие на прямойBb, проходящей через вершинуB, отображают системы с постоянным соотношением концентраций компонентовAиC.
2. Точки, лежащие на прямой, проходящей через две стороны, параллельно третьей (рис. 9.2), отображают системы с постоянным содержанием компонента, которому эта вершина отвечает. Например, в любой точке на линии OO1, содержание компонентаBодинаково (Ob3 = O1b4).
studfiles.net
Системы трехкомпонентные - Справочник химика 21
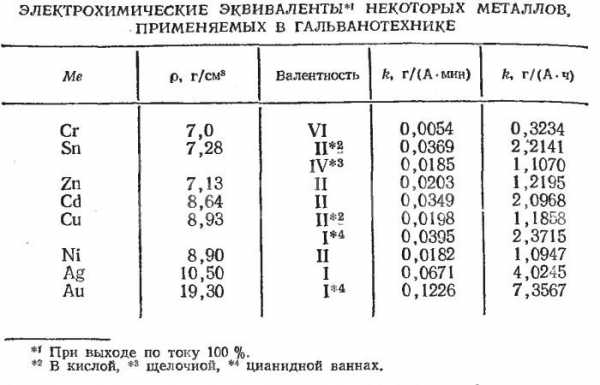
ТРОЙНЫЕ СИСТЕМЫ (трехкомпонентные системы) — физико-химич. системы, образованные тремя компонентами. Для изображения состава Т. с., в к-рых не могут идти реакции замещения или вытеснения, чаще всего пользуются равносторонним треугольником, иногда — прямоугольным треугольником, причем если состав Т. с. выражен в долях (см. Концентрация) или процентах, то пользуются равносторонним или прямоугольным равнобедренным треугольником (рис. 1). Чистым компонентам А, [c.143] Трехкомпонентные системы. Трехкомпонентные системы могут гораздо чаще встретиться в практике санитарно-химического анализа, чем двухкомпонентные. Поэтому их рефрактометрический анализ весьма актуален. [c.589]Опытные данные по равновесному распределению третьего компонента между двумя фазами можно найти в справочнике [1]. Опытные данные по равновесному распределению представляются в треугольных диаграммах (поскольку системы трехкомпонентные) или при соответствующем преобразовании треугольных диаграмм — в прямоугольных координатах. [c.29]
На рис. 350 даны изотермы растворимости в системе МН4ЫОз— —(ЫН4)2504—Н2О при О, 30, 70 и 100°. Пунктирные линии, проходящие через эвтонические точки 1, 2, з, a и >1, Ьг, з, l>i, отделяют области существования отдельных солей и двойной соли, Так как система трехкомпонентная, то при условии ее инвариантности наибольшее число фаз в ней может быть равно пяти, из которых три— твердые. Следовательно, все три твердые фазы в присутствии жидкой и парообразной фаз могут существовать одновременно лишь при одной определенной температуре, концентрации и давлении. [c.417]
Опытные данные по равновесному распределению графически представляются в треугольных диаграммах (поскольку системы трехкомпонентные). [c.37]
Система трехкомпонентная, так как в ней четыре составные части (НА, HjO, Н3О+ и А ) и одна химическая реакция. Независимые компоненты — НА и Н2О, [c.38]
В случае кристаллизации из расплава тройной солевой системы трехкомпонентных твердых растворов уравнения, описывающие ход эвтектических линий в непосредственной близости от бинарных эвтектических точек, имеют вид 5] для линии 6126123 [c.136]
Индивидуальные вещества, наименьшее число которых достаточно для образования всех фаз данной термодинамической системы, называются независимыми, компонентами (компонентами). В зависимости от числа этих компонентов различают системы однокомпонентные, двухкомпонентные (двойные системы), трехкомпонентные (тройные системы), четырехкомпонентные (четверные системы) и т. д. [c.49]
Анализ полученных значений характеристических величин свидетельствует об образовании в этих стеклообразных системах трехкомпонентных структурных единиц. Таким образом, при изучении закономерностей изменения параметров электропроводности и других физико-химических свойств в трехкомпонентных стеклообразных системах возможно выявление особенностей структурно-химического взаимодействия в соответствующих системах, выяснение возможности образования индивидуальных трехкомпонентных соединений. [c.157]
Таким образом, в результате взаимного растворения образуется двухфазная система трехкомпонентных растворов. Для каждого из них будут выполняться следующие р.авенства [c.183]
Если же между составными частями системы невозможны никакие химические реакции (физическая система), то число компонентов равно числу составных частей. Например, в равновесной гетерогенной системе хлорид натрия (кристаллический) насыщенный раствор хлорида натрия в смеси с водой и этиловым спиртом — составных частей три (Na l, HgO и С2Н5ОН). Система трехкомпонентная. [c.93]
На рис. 315 даны изотер творимости в системе N1 (ЫН4)2504—Н2О при О, 30, 70 и 100°. Пунктирные линии, проходящие через эвтонические точки Сь 2, аз, 4 и Ьи 62. Ьз, 4, отделяют области существования отдельных солей и двойной соли. Так как система трехкомпонентная, то при условии ее инвариантности наибольшее число фаз в ней может быть равно пяти, из которых три — твердые. Следовательно, все три твердые фазы в присутствии жидкой и парообразной фазы могут существовать одновременно лишь при одной определенной температуре, концентрации и давлении. Как видно из диаграммы, эта температура не находится в пределах от О до Г00°. В этом интервале температур в присутствии ж идкой фазы совместно могут существовать только две твердые фазы — двойная соль и нитрат аммония или двойная соль и сульфат аммония. [c.788]
Физическая химия (1980) -- [ c.138 ]Физическая химия. Т.1 (1980) -- [ c.335 ]
Основные процессы и аппараты химической технологии Изд.7 (1961) -- [ c.597 , c.605 ]
Руководство по физической химии (1988) -- [ c.168 , c.178 ]
Физическая химия силикатов и других тугоплавких соединений (1988) -- [ c.248 , c.275 ]
Жидкостная экстракция (1966) -- [ c.0 ]
Курс физической химии Том 1 Издание 2 (1969) -- [ c.398 ]
Курс физической химии Том 1 Издание 2 (копия) (1970) -- [ c.398 ]
Химическая термодинамика Издание 2 (1953) -- [ c.334 , c.338 ]
Физическая и коллоидная химия (1964) -- [ c.202 , c.211 ]
Справочник по разделению газовых смесей методом глубокого охлаждения (1963) -- [ c.0 , c.234 , c.262 ]
Справочник по разделению газовых смесей (1953) -- [ c.182 ]
chem21.info
6. Трехкомпонентные системы.
На практике наряду с двухкомпонентными системами гораздо чаще приходится иметь дело с системами, составленными из трех и более компонентов.
Уравнение состояния трехкомпонентных систем связывает между собой пять параметров и имеет следующий вид:
. (6.12)
Из (6.12) следует, что диаграмма состояния трехкомпонентной системы не может быть изображена на плоскости.
Полагая, что Р = const и С1 + С2 + С3 = 1, если способ выражения состава сплавов мольные доли, трехкомпонентную диаграмму можно построить в трехмерном пространстве.
Составы трехкомпонентных сплавов принято изображать на плоскости с помощью концентрационного треугольника. В вершинах треугольника располагаются чистые компоненты А, В и С, а три его стороны отражают составы двойных сплавов. Ось, перпендикулярная плоскости концентрационнго треугольника - температурная ось.
Свойства концентрационного треугольника.
Первое свойство. Если из какой-то точки М, лежащей в плоскости треугольника опустить три перпендикуляра на стороны, то:
МА + МВ + МС = const = BD,
где BD - высота концентрационного треугольника (рис. 6.9, а).
Если BD принять за 100%, то каждый из перпендикуляров - концентрация каждого из компонентов в сплаве:
Ма = % А; Мb = % B; Mc = % C.
Второе свойство. Если через точку М, лежащей в плоскости треугольника, провести три
параллельные сторонам треугольника прямые, то сумма отрезков Аb, Bc и Са, отсекаемых этими прямыми на сторонах треугольника - величина постоянная и равная стороне треугольника:
Аb + Вс + Са = const = АВ.
Если АВ = % В, Вс = % С и Са = % А, то состав трехкомпонентного сплава определен.
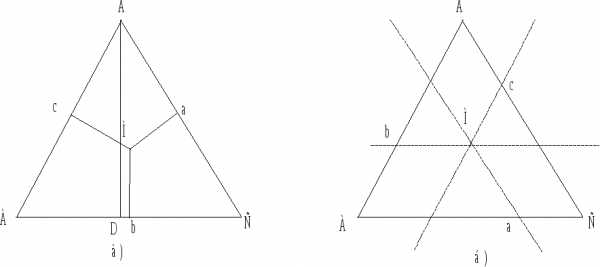
Рис. 6.9. Свойства равностороннего треугольника, применяемого
для изображения составов трехкомпонентных сплавов.
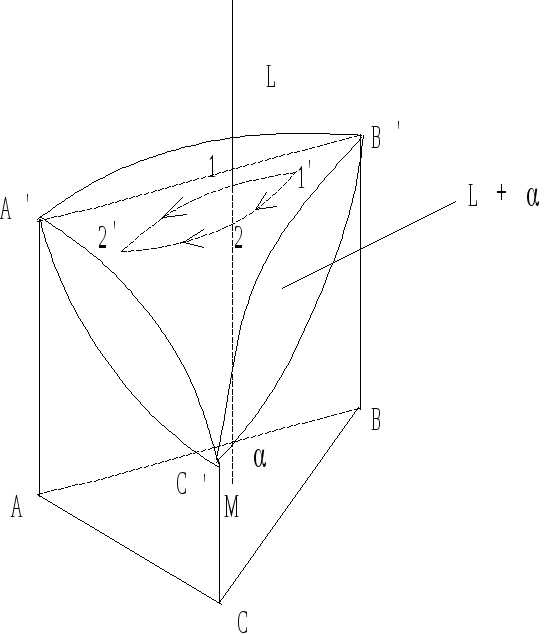
Как и для двухкомпонентных систем, сложность диаграмм состояния трехкомпонентных систем зависит от взаимной растворимости компонентов и от возможности образования между ними химических соединений.
Наиболее простой является диаграмма состояния трехкомпонентной системы с неограниченной растворимостью компонентов в жидком и твердом состояниях (рис. 6.10).
Для диаграммы на рис. 6.10 ТS (B) > ТS (A) > ТS (С) т. А’, B’ и C’ - температуры плавления чистых компонентов.
Рис. 6.10. Диаграмма состояния тройной системы с неограниченной растворимостью компонентов в жидком и твердом состояниях.
Грани призмы - двойные системы с неограниченной растворимостью компонентов в твердом и жидком состояниях. Через три ликвидуса проходит поверхность ликвидуса. Выше поверхности ликвидуса находится объем жидких растворов (L). Через три солидуса проходит поверхность солидуса. Ниже поверхности солидуса располагается объем твердых растворов (). Объем пространства между поверхностями ликвидуса и солидуса занят равновесной двухфазной системой из жидких и твердых растворов (L +). Интервал между поверхностью ликвидуса и солидуса - интервал кристаллизации (плавления) сплавов трехкомпонентной системы.Сплав состава т. М (рис. 6.10) при Т > Т1 находится в состоянии ненасыщенного жидкого раствора. Кристаллизация сплава начинается при Т1, лежащей на поверхности ликвидуса. Состав первых кристаллов - твердого раствора соответствует проекции точки 1’ на плоскость концентрационного треугольника.
При дальнейшем понижении температуры от Т1 до Т2 жидкость постепенно принимает состав т. 2’ и исчезает, а кристаллы - твердого раствора - т. 2. Поэтому процесс кристаллизации сплава изображается уравнением вида:
. (6.10)
Ниже температуры Т2 происходит охлаждение кристаллов твердого раствора .
При работе с диаграммами состояния трехкомпонентных систем удобно пользоваться их разрезами - поли- и изотермическими. Изотермические разрезы характеризуют фазовые равновесия в тройных сплавах, а по политермическим разрезам устанавливают температуры начала и конца кристаллизации сплавов и т.д.
_______
В данной главе рассмотрен ряд более или менее сложных систем, изучение которых с помощью лишь одного термодинамического метода затруднено. С помощью же диаграмм состояния свойства таких систем описывать достаточно просто. Но лишь параллельное применение термодинамического метода и основных позиций физико-химического анализа, с помощью которого строятся диаграммы состояния, позволяет получить весьма глубокую информацию об изучаемой системе. Однако всегда необходимо помнить, что большей частью рассматриваются лишь равновесные системы. Именно для таких систем изображаются соответствующие диаграммы состояния. Количество и конкретный вид фаз сложной системы, наблюдаемые на практике, могут в действительности сильно отличаться от равновесных, вследствие торможения процесса перехода в равновесное состояние.
studfiles.net
6. Трехкомпонентные системы.
На практике наряду с двухкомпонентными системами гораздо чаще приходится иметь дело с системами, составленными из трех и более компонентов.
Уравнение состояния трехкомпонентных систем связывает между собой пять параметров и имеет следующий вид:
. (6.12)
Из (6.12) следует, что диаграмма состояния трехкомпонентной системы не может быть изображена на плоскости.
Полагая, что Р = const и С1 + С2 + С3 = 1, если способ выражения состава сплавов мольные доли, трехкомпонентную диаграмму можно построить в трехмерном пространстве.
Составы трехкомпонентных сплавов принято изображать на плоскости с помощью концентрационного треугольника. В вершинах треугольника располагаются чистые компоненты А, В и С, а три его стороны отражают составы двойных сплавов. Ось, перпендикулярная плоскости концентрационнго треугольника - температурная ось.
Свойства концентрационного треугольника.
Первое свойство. Если из какой-то точки М, лежащей в плоскости треугольника опустить три перпендикуляра на стороны, то:
МА + МВ + МС = const = BD,
где BD - высота концентрационного треугольника (рис. 6.9, а).
Если BD принять за 100%, то каждый из перпендикуляров - концентрация каждого из компонентов в сплаве:
Ма = % А; Мb = % B; Mc = % C.
Второе свойство. Если через точку М, лежащей в плоскости треугольника, провести три
параллельные сторонам треугольника прямые, то сумма отрезков Аb, Bc и Са, отсекаемых этими прямыми на сторонах треугольника - величина постоянная и равная стороне треугольника:
Аb + Вс + Са = const = АВ.
Если АВ = % В, Вс = % С и Са = % А, то состав трехкомпонентного сплава определен.
Рис. 6.9. Свойства равностороннего треугольника, применяемого
для изображения составов трехкомпонентных сплавов.
Как и для двухкомпонентных систем, сложность диаграмм состояния трехкомпонентных систем зависит от взаимной растворимости компонентов и от возможности образования между ними химических соединений.
Наиболее простой является диаграмма состояния трехкомпонентной системы с неограниченной растворимостью компонентов в жидком и твердом состояниях (рис. 6.10).
Для диаграммы на рис. 6.10 ТS (B) > ТS (A) > ТS (С) т. А’, B’ и C’ - температуры плавления чистых компонентов.
Рис. 6.10. Диаграмма состояния тройной системы с неограниченной растворимостью компонентов в жидком и твердом состояниях.
Грани призмы - двойные системы с неограниченной растворимостью компонентов в твердом и жидком состояниях. Через три ликвидуса проходит поверхность ликвидуса. Выше поверхности ликвидуса находится объем жидких растворов (L). Через три солидуса проходит поверхность солидуса. Ниже поверхности солидуса располагается объем твердых растворов (). Объем пространства между поверхностями ликвидуса и солидуса занят равновесной двухфазной системой из жидких и твердых растворов (L +). Интервал между поверхностью ликвидуса и солидуса - интервал кристаллизации (плавления) сплавов трехкомпонентной системы.Сплав состава т. М (рис. 6.10) при Т > Т1 находится в состоянии ненасыщенного жидкого раствора. Кристаллизация сплава начинается при Т1, лежащей на поверхности ликвидуса. Состав первых кристаллов - твердого раствора соответствует проекции точки 1’ на плоскость концентрационного треугольника.
При дальнейшем понижении температуры от Т1 до Т2 жидкость постепенно принимает состав т. 2’ и исчезает, а кристаллы - твердого раствора - т. 2. Поэтому процесс кристаллизации сплава изображается уравнением вида:
. (6.10)
Ниже температуры Т2 происходит охлаждение кристаллов твердого раствора .
При работе с диаграммами состояния трехкомпонентных систем удобно пользоваться их разрезами - поли- и изотермическими. Изотермические разрезы характеризуют фазовые равновесия в тройных сплавах, а по политермическим разрезам устанавливают температуры начала и конца кристаллизации сплавов и т.д.
_______
В данной главе рассмотрен ряд более или менее сложных систем, изучение которых с помощью лишь одного термодинамического метода затруднено. С помощью же диаграмм состояния свойства таких систем описывать достаточно просто. Но лишь параллельное применение термодинамического метода и основных позиций физико-химического анализа, с помощью которого строятся диаграммы состояния, позволяет получить весьма глубокую информацию об изучаемой системе. Однако всегда необходимо помнить, что большей частью рассматриваются лишь равновесные системы. Именно для таких систем изображаются соответствующие диаграммы состояния. Количество и конкретный вид фаз сложной системы, наблюдаемые на практике, могут в действительности сильно отличаться от равновесных, вследствие торможения процесса перехода в равновесное состояние.
1Людвиг Больцман (1841 - 1906 г.г.), австрийский физик, один из основоположников статистической физики и физической кинетики.
53
studfiles.net
