Содержание
Цилиндр и его сечения (квадрат и вписанный куб)
Примечание. Это урок с решениями задач по геометрии (раздел цилиндр). Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. В задачах вместо символа «квадратный корень» применяется функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак «√».
Задача
Осевое сечение цилиндра — квадрат, диагональ которого равна 4√2.
Вычислить объем цилиндра.
Решение.
Поскольку диагональ сечения цилиндра — квадрат, то обозначим его сторону как a.
a2 + a2 = (4√2)2
2a2 = 32
a2 = 16
a = 4
Объем цилиндра найдем по формуле:
V = πd2 / 4 * h
откуда
V = π42 / 4 * 4
V = 16π
Ответ: Объем цилиндра равен 16π
Задача
Куб с ребром длиной а вписан в цилиндр. Найдите площадь осевого сечения цилиндра.
Найдите площадь осевого сечения цилиндра.
Решение.
Проведем плоскость через основание цилиндра.
Диагональ куба является одновременно диаметром цилиндра. Зная сторону куба, определяем длину диагонали AC квадрата ABCD как
CD2 + AD2= AC2
a2 + a2 = AC2
2a2 = AC
AC = a√2
Проведем плоскость через ось цилиндра по диагонали AC. Высота сечения равна длине ребра куба и по условиям задачи рана а, а ширина сечения равна a√2.
Таким образом, площадь сечения равна:
S = a * a√2 = a2√2
Ответ: a2√2
Задача
Диагональ осевого сечения цилиндра равна 12 см и образует с плоскостью нижнего основания угол 45 градусов. Найти обьём цилиндра.
Решение.
Поскольку основание осевого сечения образует с высотой цилиндра, принадлежащей сечению, прямой угол, то треугольник, который образован диагональю осевого сечения, высотой цилиндра и его диаметром — прямоугольный.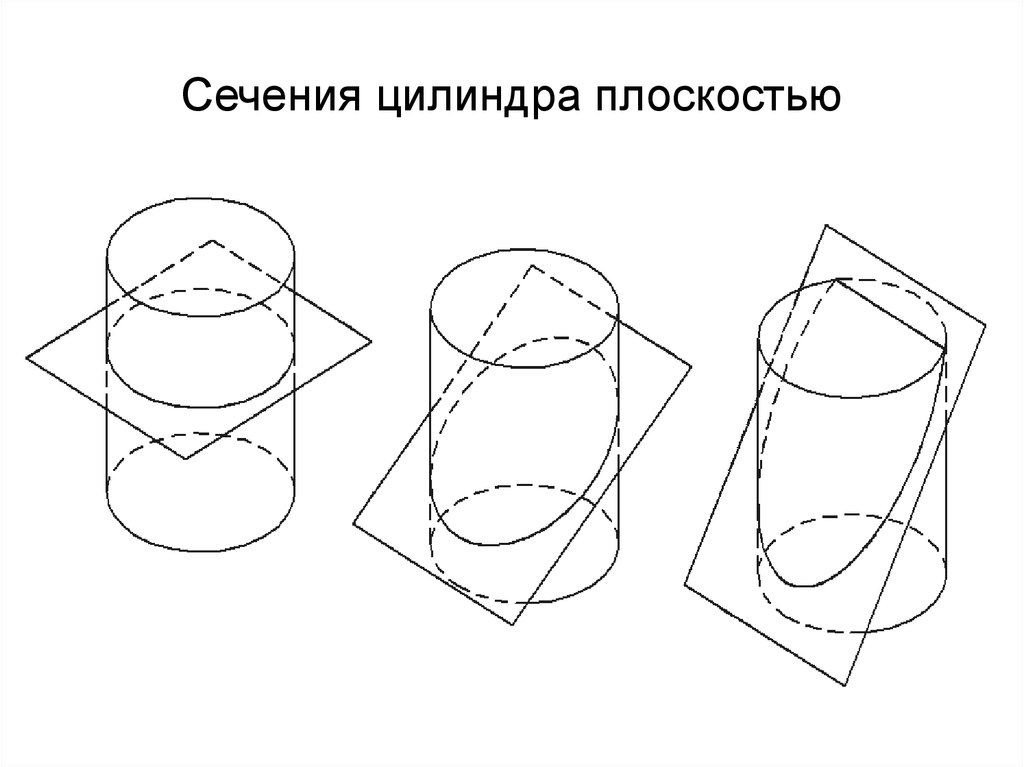
Исходя из этого, угол между диагональю и высотой также равен 45 градусов ( 180 — 90 — 45 ).
Таким образом, треугольник является равнобедренным, а, следовательно, высота цилиндра равна его диаметру. Применив теорему Пифагора, найдем их.
d2 + d2 = 122
2d2 = 144
d2 = 72
Теперь применим формулу объема цилиндра V = пd2 / 4 h
V = 72п / 4 * √72
V = 18п * √72
Ответ: 18п√72
Задача
|
|
|
Решение. Рiшення.
|
В силу симметричности квадрата и цилиндра и ввиду того, что квадрат наклонный, диагональ квадрата пересечет ось цилиндра ОО1 в точке М, являющейся серединой отрезкаОО1. По условию ОО1=2м, а ОА=7 м, поэтому ОМ=1м.
|
У силу симетричності квадрата і циліндра і зважаючи на те, що квадрат похилий, діагональ квадрата перетне вісь циліндра ОО1 в точці М, яка є серединою відрізка ОО1. За умовою ОО1=2м, а ОА=7 м, тому ОМ=1м. 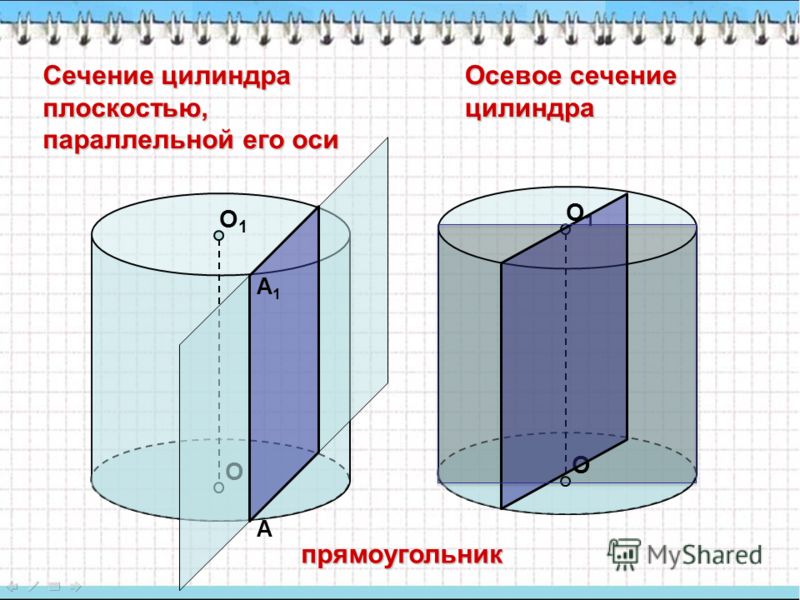
|
0
Цилиндр и его сечения |
Описание курса
| Диагональ цилиндра
Запчасти для Амкодор-342С в узле «Цилиндр рулевой» в разрезе схемы №43-2731
Главная / Электронные каталоги / Для фронтальных погрузчиков Амкодор / Амкодор-342С /Цилиндр рулевой
Электронные каталоги
1
2
3
4
5
6
7
8
Технические
консультации
Принимаем к оплате наличные, карты и банковские переводы
Бесплатная
доставка
| № | Фото | Код | Наименование | Цена / шт.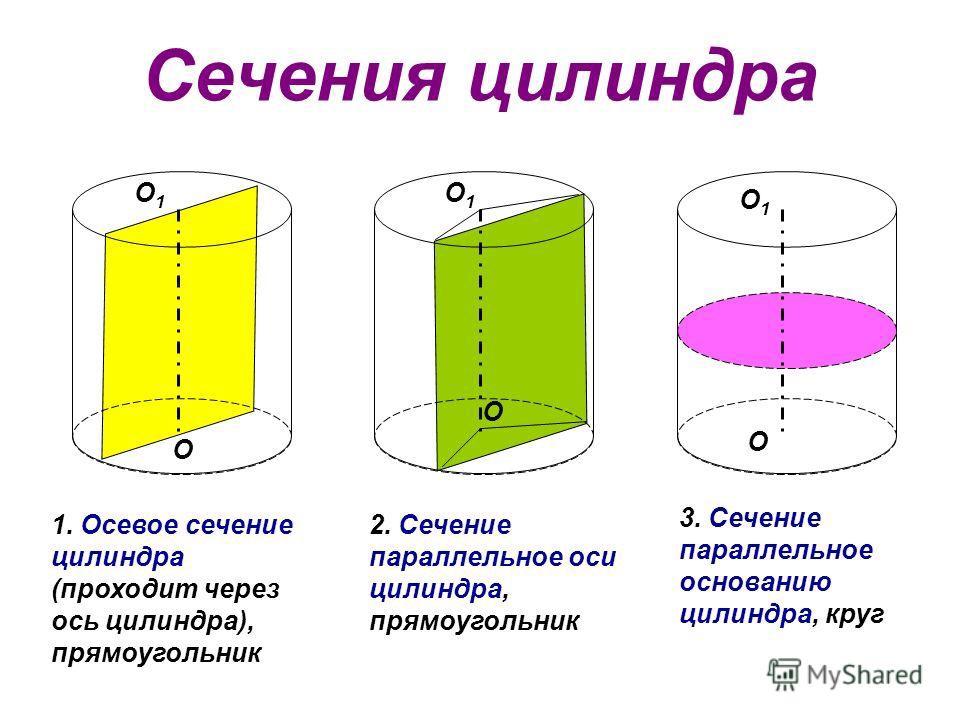 | Наличие | В узле | |
|---|---|---|---|---|---|---|---|
| 1 | 09576033 | Гидроцилиндр рулевой ТО-28А.78.08.000 | 61 256 р. | Поставим за 3 дня | В корзину | ||
| 2 | 07020194 | Кольцо 032-040-46 | 30 р. | В наличии 36 шт. | В корзину | ||
| 3 | 07020424 | Кольцо 072-080-46 | 89 р. | Поставим за 3 дня | В корзину | ||
| 4 | 05520250 | Кольцо стопорное внутреннее В 62 (ГОСТ 13943-86) в отверстие под ШС-40 | 51 р. | В наличии 129 шт. | В корзину | ||
| 5 | 00000324 | Подшипник ШСЛ-40 | — | Поставим за 3 дня | В корзину | ||
| 6 | 07070460 | Ремкомплект рулевого гидроцилиндра (80х40 немецкие уплотнения) | 1 390 р.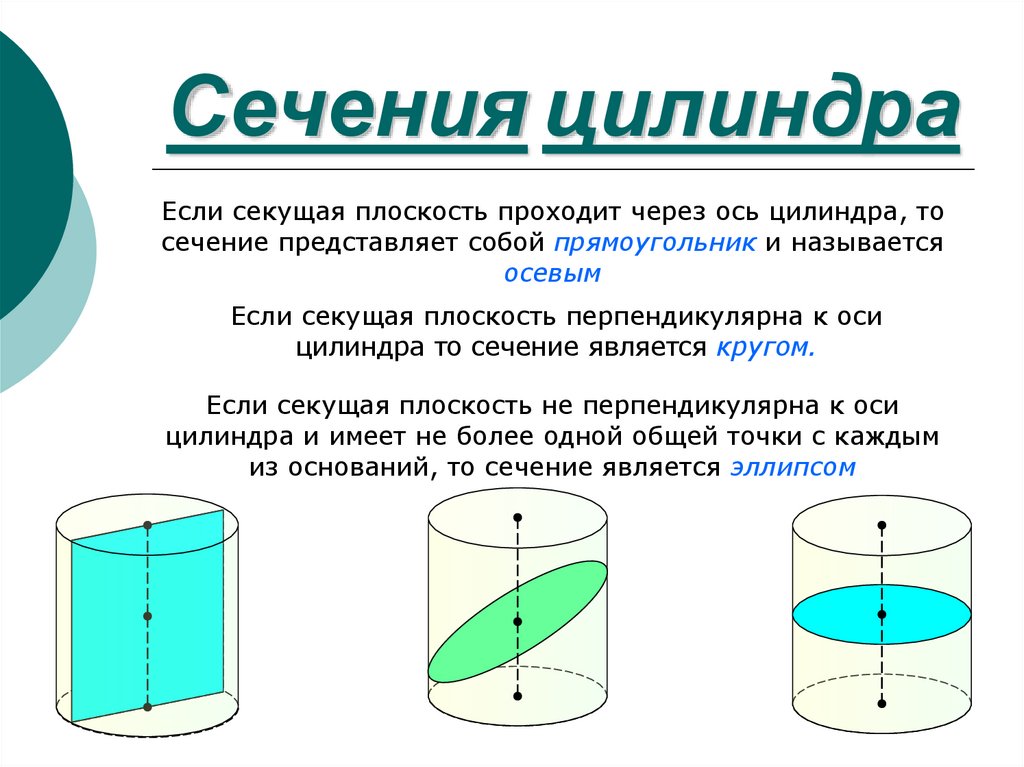 | В наличии 25 шт. | В корзину | ||
| 7 | 1512241 | Ремкомплект рулевого гидроцилиндра (80х40 уплотнения Элконт) | 1 958 р. | В наличии 4 шт. | В корзину | ||
| 8 | 07070440 | Ремкомплект рулевого гидроцилиндра (80х56 уплотнения Элконт) | 1 390 р. | В наличии 10 шт. | В корзину |
Возможно, Вас заинтересует:
амкодор 211
Как рассчитать площадь поперечного сечения
Обновлено 7 февраля 2020 г.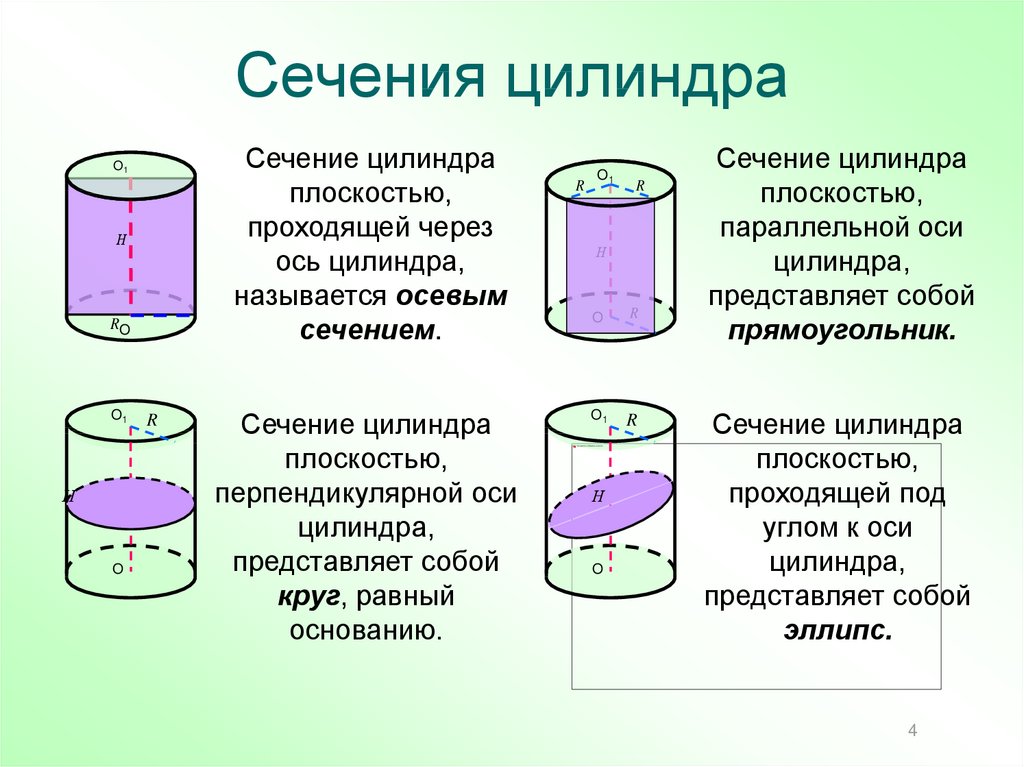
Кевин Бек
Вы можете столкнуться с ситуациями, когда у вас есть трехмерная твердотельная фигура и вам нужно вычислить площадь воображаемой плоскости, вставленной через фигуру и имеющей границы, определяемые границами твердого тела.
Например, если под вашим домом проходит цилиндрическая труба длиной 20 метров (м) и диаметром 0,15 м, вам может понадобиться узнать площадь поперечного сечения трубы.
Поперечные сечения могут быть перпендикулярны оси твердого тела, если таковые существуют. В случае сферы любая секущая плоскость, проходящая через сферу, независимо от ориентации, приведет к диску определенного размера.
Площадь поперечного сечения зависит от формы твердого тела, определяющей границы поперечного сечения, и угла между осью симметрии твердого тела (если она есть) и плоскостью, создающей поперечное сечение.
Площадь поперечного сечения прямоугольного тела
Объем любого прямоугольного тела, включая куб, равен площади его основания (длина, умноженная на ширину), умноженной на его высоту: V = l × w × h.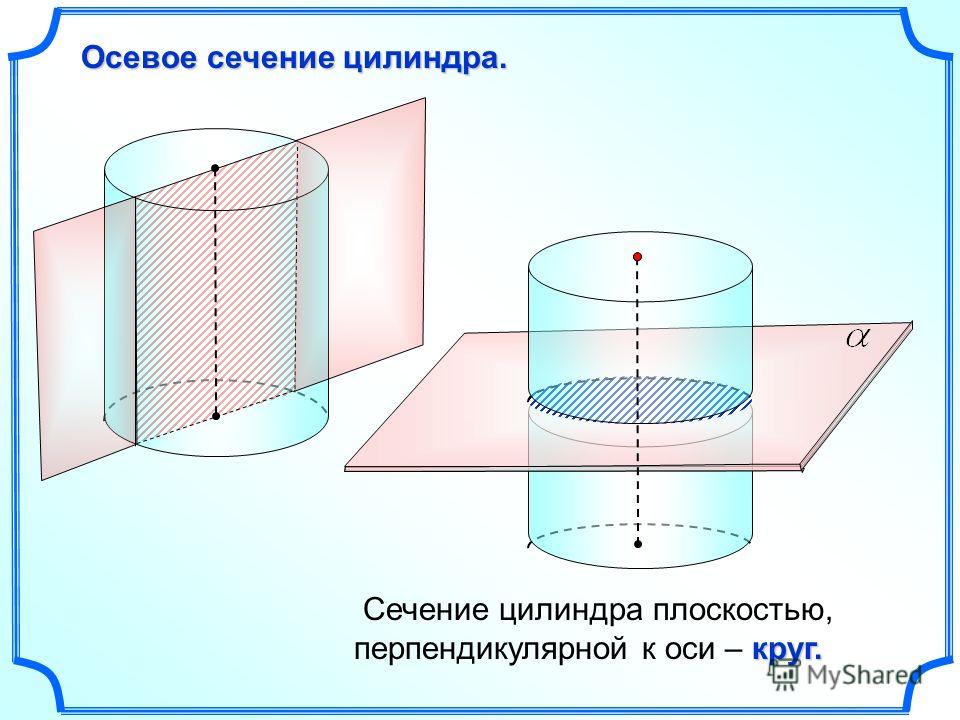
Следовательно, если поперечное сечение параллельно верхней или нижней части твердого тела, площадь поперечного сечения равна l × w. Если секущая плоскость параллельна одному из двух наборов сторон, площадь поперечного сечения вместо этого определяется как l × h или w × h.
Если поперечное сечение не перпендикулярно какой-либо оси симметрии, созданная форма может быть треугольником (если провести через угол тела) или даже шестиугольником.
Пример: Вычислить площадь поперечного сечения плоскости, перпендикулярной основанию куба объемом 27 м 3 .
Так как для куба l = w = h, длина любого ребра куба должна быть 3 м (поскольку 3
× 3
× 3 = 27). Таким образом, поперечное сечение описанного типа представляет собой квадрат со стороной 3 м, что дает площадь 9 м 2 .
Площадь поперечного сечения цилиндра
Цилиндр представляет собой твердое тело, образованное путем вытягивания окружности через пространство перпендикулярно ее диаметру.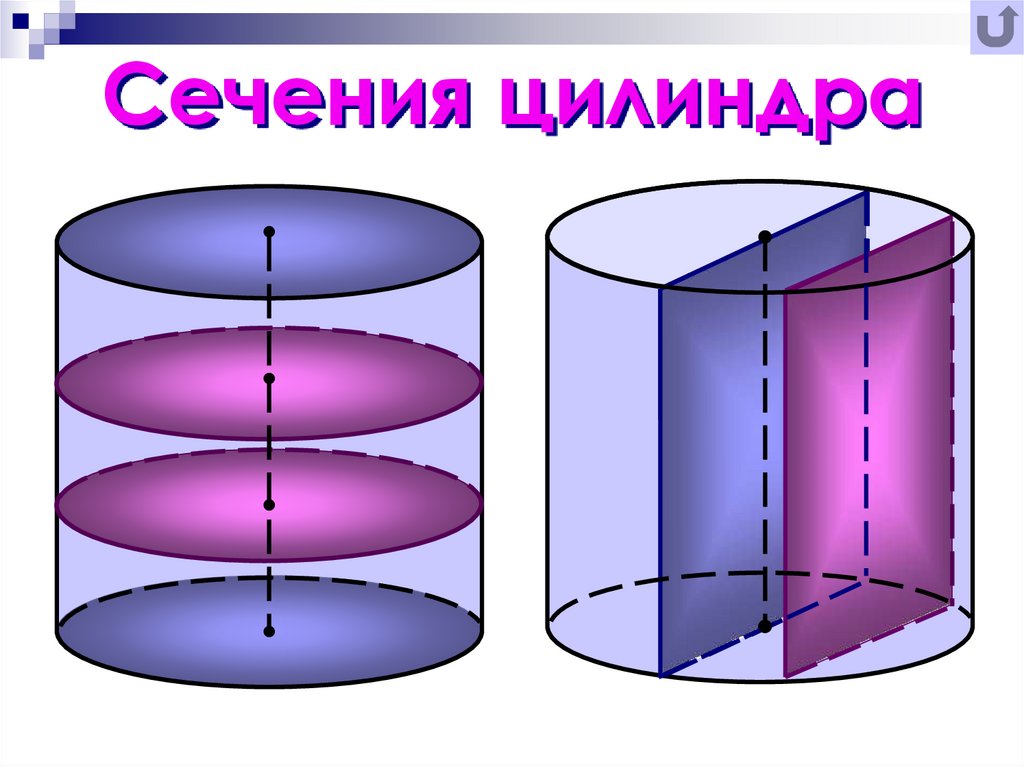 Площадь круга находится по формуле πr 2 , где r — радиус. Поэтому имеет смысл, что объем цилиндра будет площадью одной из окружностей, образующих его основание.
Площадь круга находится по формуле πr 2 , где r — радиус. Поэтому имеет смысл, что объем цилиндра будет площадью одной из окружностей, образующих его основание.
Если поперечное сечение параллельно оси симметрии, то площадь поперечного сечения представляет собой просто круг площадью πr 2 . Если секущая плоскость вставляется под другим углом, создается эллипс. Для площади используется соответствующая формула: πab (где a — самое большое расстояние от центра эллипса до края, а b — самое короткое).
Пример: Какова площадь поперечного сечения трубы под вашим домом, описанной во введении?
Площадь поперечного сечения сферы
Любая теоретическая плоскость, проведенная через сферу, даст круг (подумайте об этом несколько минут). Если вы знаете диаметр или длину окружности, образуемой поперечным сечением, вы можете использовать соотношения C = 2πr и A = πr 2 для получения решения.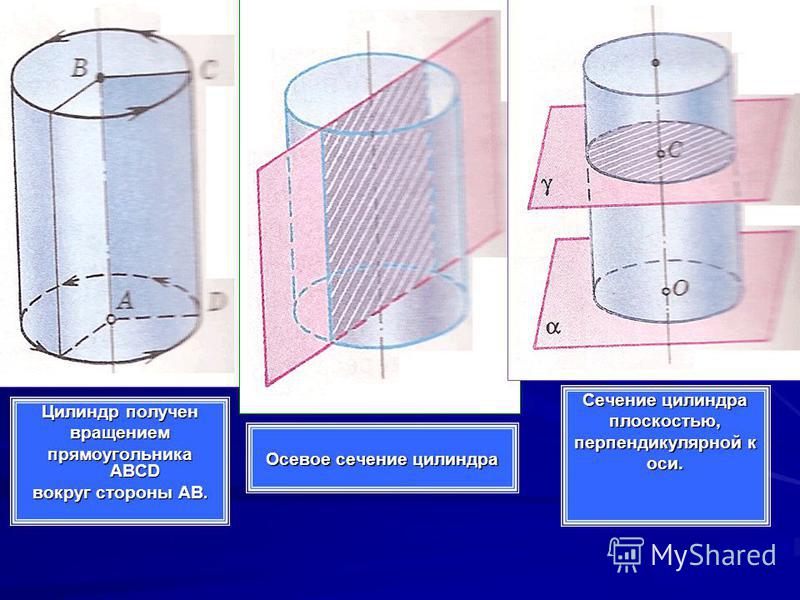
Пример 900:12: Самолет грубо вставлен в Землю очень близко к Северному полюсу, удаляя часть планеты в 10 м вокруг. Какова площадь поперечного сечения этого холодного куска Земли?
- Поскольку C = 2πr = 10 м, r = 10/2π = 1,59 м; A = πr 2 = π(1,59) 2 = 7,96 м 2 .
Как рассчитать высоту по объему
••• wutwhanfoto/iStock/GettyImages
Обновлено 30 апреля 2018 г.
Автор: Chance E. Gartneer
Высота является интегральным размером при определении объема объекта. Чтобы найти измерение высоты объекта, вам нужно знать его геометрическую форму, такую как куб, прямоугольник или пирамида. Один из самых простых способов думать о высоте, поскольку она соответствует объему, — это думать о других измерениях как о базовой площади. Высота — это просто множество базовых областей, сложенных друг на друга. Формулы объема отдельных объектов можно изменить для расчета высоты. Математики давно вывели формулы объема для всех известных геометрических фигур.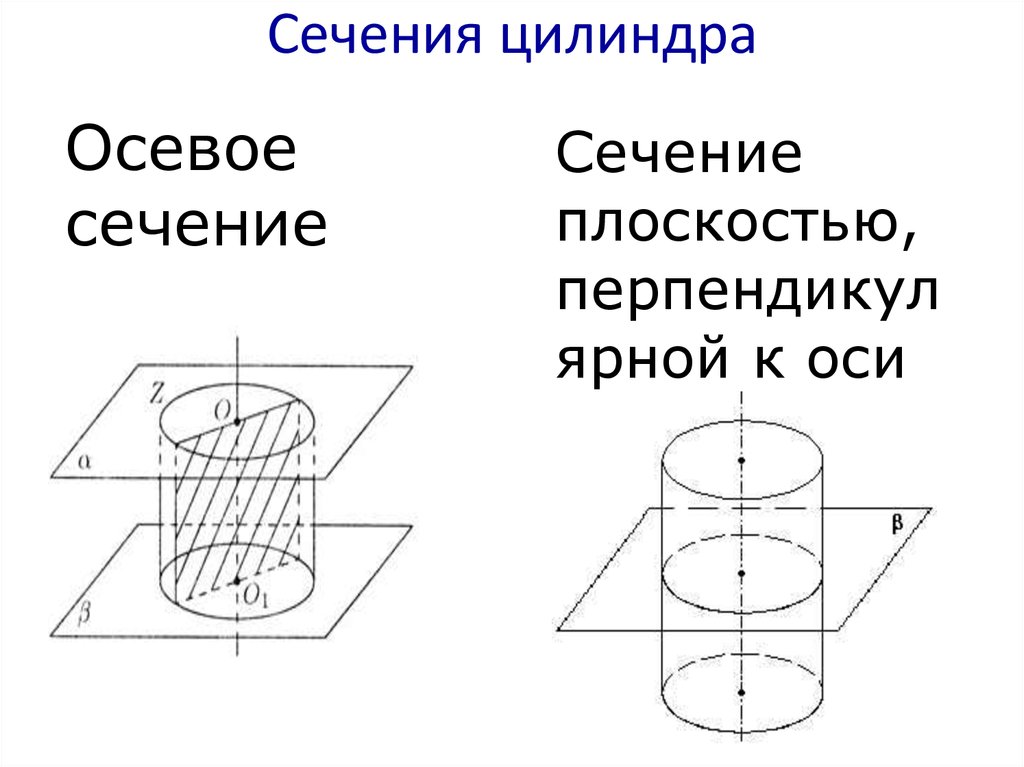 В некоторых случаях, например, в случае с кубом, определить высоту несложно; в других требуется немного простой алгебры.
В некоторых случаях, например, в случае с кубом, определить высоту несложно; в других требуется немного простой алгебры.
Высота прямоугольных объектов
Формула объема сплошного прямоугольника: ширина x глубина x высота. Разделите объем на произведение длины и ширины, чтобы вычислить высоту прямоугольного объекта. В этом примере прямоугольный объект имеет длину 20, ширину 10 и объем 6000. Произведение 20 и 10 равно 200, а 6000, разделенное на 200, дает 30. Высота объекта равна 30.
Высота куба
Куб — это разновидность прямоугольника, у которого все стороны одинаковы. Итак, чтобы найти объем, возведите в куб длину любой стороны. Чтобы найти высоту, вычислите кубический корень из объема куба. В этом примере объем куба равен 27. Кубический корень из 27 равен 3. Высота куба равна 3,9.2) умножить на высоту. Разделите объем цилиндра на квадрат радиуса, умноженный на число Пи, чтобы вычислить его высоту.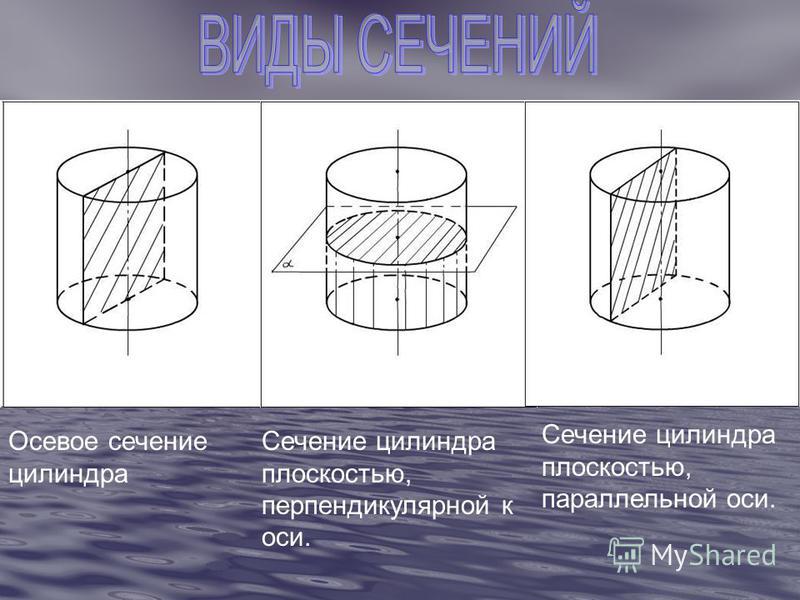 В этом примере объем цилиндра равен 300, а радиус равен 3. Возведение 3 в квадрат дает 9, а умножение 9 на число пи дает 28,274. Разделив 300 на 28,274, мы получим 10,61. Высота цилиндра 10,61.
В этом примере объем цилиндра равен 300, а радиус равен 3. Возведение 3 в квадрат дает 9, а умножение 9 на число пи дает 28,274. Разделив 300 на 28,274, мы получим 10,61. Высота цилиндра 10,61.
Высота пирамиды
Квадратная пирамида имеет плоское квадратное основание и четыре треугольные стороны, которые сходятся в точке на вершине. Формула объема: длина x ширина x высота ÷ 3. Утройте объем пирамиды, а затем разделите это количество на площадь основания, чтобы вычислить ее высоту. В этом примере объем пирамиды равен 200, а площадь ее основания равна 30. Умножение 200 на 3 дает 600, а деление 600 на 30 дает 20. Высота пирамиды 20,9.0003
Высота призмы
Геометрия описывает несколько различных видов призм: одни имеют прямоугольные основания, другие — треугольные. В любом случае поперечное сечение на всем протяжении одинаково, как и у цилиндра. Объем призмы равен произведению площади основания на высоту. Итак, чтобы вычислить высоту, разделите объем призмы на площадь ее основания.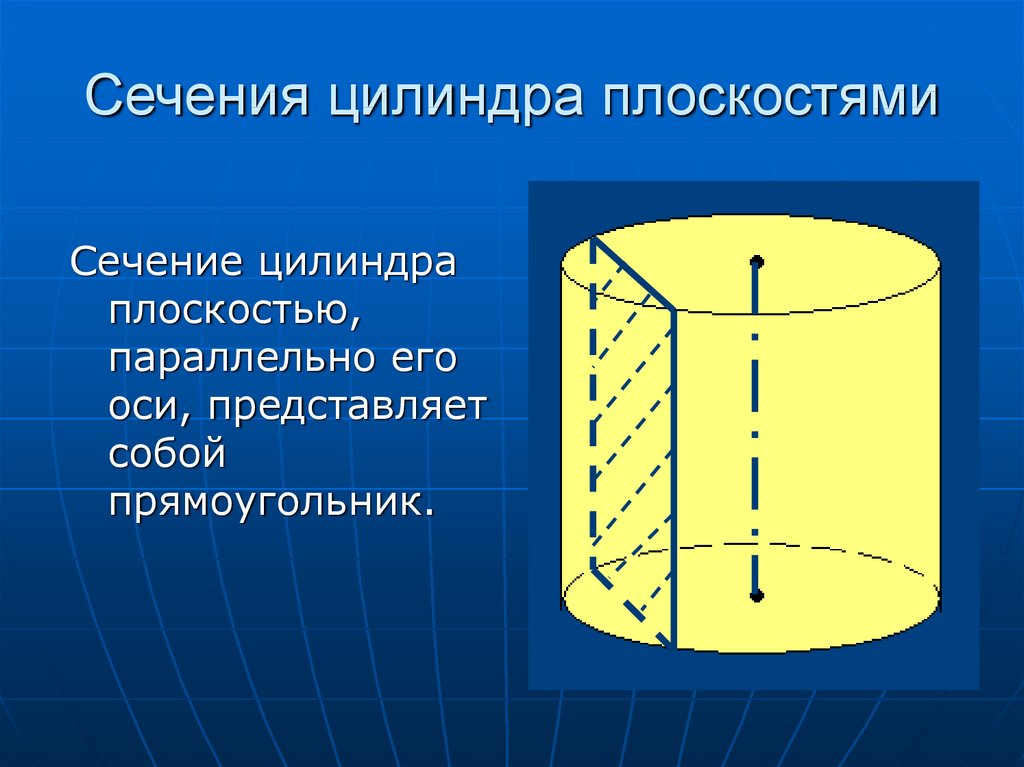
 Знайти сторону квадрата.
Знайти сторону квадрата.