Пирамида и усеченная пирамида. Изобразите усеченную четырехугольную пирамиду

Пирамида и усеченная пирамида

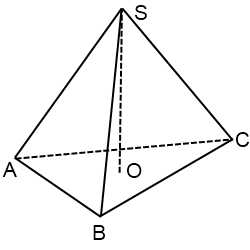
Как можно построить пирамиду? На плоскости р построим какой-либо многоугольник, например пятиугольник ABCDE. Вне плоскости р возьмем точку S. Соединив точку S отрезками со всеми точками многоугольника, получим пирамиду SABCDE (рис.).

Точка S называется вершиной, а многоугольник ABCDE — основанием этой пирамиды. Таким образом, пирамида с вершиной S и основанием ABCDE — это объединение всех отрезков [SM], где М ∈ ABCDE.

Треугольники SAB, SBC, SCD, SDE, SEA называются боковыми гранями пирамиды, общие стороны боковых граней SA, SB, SC, SD, SE — боковыми ребрами.

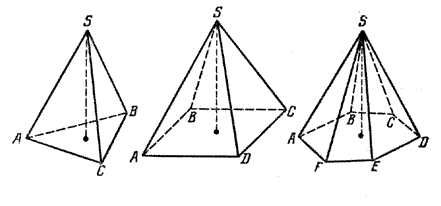
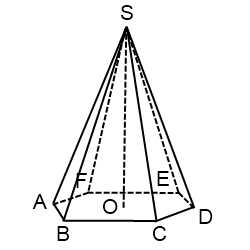
Пирамиды называются треугольными, четырехугольными, п-угольными в зависимости от числа сторон основания. На рис. даны изображения треугольной, четырехугольной и шестиугольной пирамид.

Плоскость, проходящая через вершину пирамиды и диагональ основания, называется диагональной, а полученное сечение — диагональным. На рис. 186 одно из диагональных сечений шестиугольной пирамиды заштриховано.

Отрезок перпендикуляра, проведенного через вершину пирамиды к плоскости ее основания, называется высотой пирамиды (концами этого отрезка являются вершина пирамиды и основание перпендикуляра).

Пирамида называется правильной, если основание пирамиды—правильный многоугольник и вершина пирамиды проектируется в его центр.

Все боковые грани правильной пирамиды — конгруэнтные равнобедренные треугольники. У правильной пирамиды все боковые ребра конгруэнтны.

Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой пирамиды. Все апофемы правильной пирамиды конгруэнтны.

Если обозначить сторону основания через а, а апофему через h, то площадь одной боковой грани пирамиды равна 1/2 ah .

Сумма площадей всех боковых граней пирамиды называется площадью боковой поверхности пирамиды и обозначается через Sбок.

Так как боковая поверхность правильной пирамиды состоит из n конгруэнтных граней, то

Sбок. = 1/2 ahn = Ph/2,

где Р — периметр основания пирамиды. Следовательно,

Sбок. = Ph/2

т. е. площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

Площадь полной поверхности пирамиды вычисляется по формуле

S = Socн. + Sбок..

Объем пирамиды равен одной трети произведения площади ее основания Socн. на высоту Н:

V = 1/3 Socн. Н.

Вывод этой и некоторых других формул будет дан в одной из последующих глав.

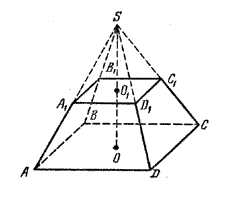
Построим теперь пирамиду другим способом. Пусть дан многогранный угол, например, пятигранный, с вершиной S (рис.).

Проведем плоскость р так, чтобы она пересекала все ребра данного многогранного угла в разных точках А, В, С, D, Е (рис.). Тогда пирамиду SABCDE можно рассматривать как пересечение многогранного угла и полупространства с границей р, в котором лежит вершина S.

Очевидно, что число всех граней пирамиды может быть произвольным, но не меньшим четырех. При пересечении трехгранного угла плоскостью получается треугольная пирамида, у которой четыре грани. Любую треугольную пирамиду иногда называют тетраэдром, что означает четырехгранник.

Усеченную пирамиду можно получить, если пирамиду пересечь плоскостью, параллельной плоскости основания.

На рис. дано изображение четырехугольной усеченной пирамиды.

Усеченные пирамиды также называются треугольными, четырехугольными, n-угольными в зависимости от числа сторон основания. Из построения усеченной пирамиды следует, что она имеет два основания: верхнее и нижнее. Основания усеченной пирамиды — два многоугольника, стороны которых попарно параллельны. Боковые грани усеченной пирамиды — трапеции.

Высотой усеченной пирамиды называется отрезок перпендикуляра, проведенного из любой точки верхнего основания к плоскости нижнего.

Правильной усеченной пирамидой называется часть правильной пирамиды, заключенная между основанием и плоскостью сечения, параллельной основанию. Высота боковой грани правильной усеченной пирамиды (трапеции) называется апофемой.

Можно доказать, что у правильной усеченной пирамиды боковые ребра конгруэнтны, все боковые грани конгруэнтны, все апофемы конгруэнтны.

Если в правильной усеченной n-угольной пирамиде через а и bn обозначить длины сторон верхнего и нижнего оснований, а через h — длину апофемы, то площадь каждой боковой грани пирамиды равна

1/2( а + bn ) h

Сумма площадей всех боковых граней пирамиды называется площадью ее боковой поверхности и обозначается Sбок. . Очевидно, что для правильной усеченной n-угольной пирамиды

Sбок. = n • 1/2( а + bn ) h .

Так как па = Р и nbn= Р1 — периметры оснований усеченной пирамиды, то

Sбок. = 1/2 (Р + Р1) h ,

т. е. площадь боковой поверхности правильной усеченной пирамиды равна половине произведения суммы периметров ее оснований на апофему.

Сечение, параллельное основанию пирамиды

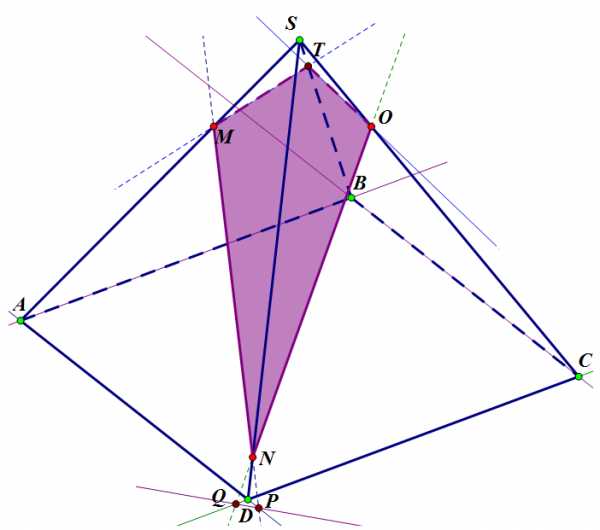
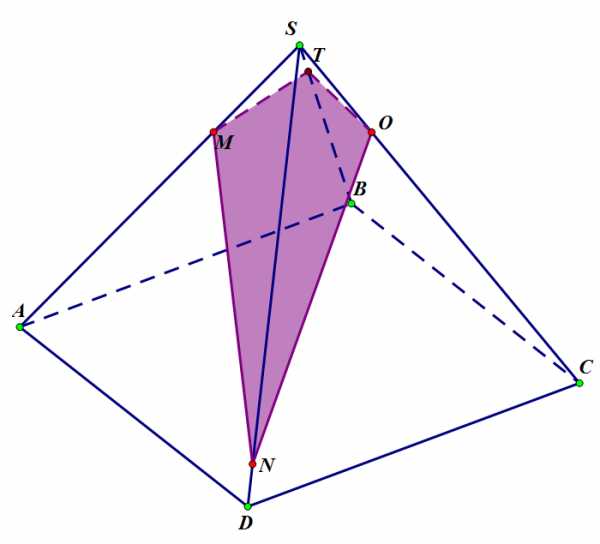
Теорема. Если пирамиду пересечь плоскостью, параллельной основанию, то:

1) боковые ребра и высота разделятся на пропорциональные части;

2) в сечении получится многоугольник, подобный основанию;

3) площади сечения и основания относятся, как квадраты их расстояний от вершины.

Теорему достаточно доказать для треугольной пирамиды.

Так как параллельные плоскости пересекаются третьей плоскостью по параллельным прямым, то (АВ) || (А1В1), (BС) ||( В1C1), (AС) || (A1С1) (рис.).

Параллельные прямые рассекают стороны угла на пропорциональные части, и поэтому

$$ \frac{\left|{SA}\right|}{\left|{SA_1}\right|}=\frac{\left|{SB}\right|}{\left|{SB_1}\right|}=\frac{\left|{SC}\right|}{\left|{SC_1}\right|} $$

Следовательно, ΔSAB ~ ΔSA1B1 и

$$ \frac{\left|{AB}\right|}{\left|{A_{1}B_1}\right|}=\frac{\left|{SB}\right|}{\left|{SB_1}\right|} $$

ΔSBC ~ ΔSB1C1 и

$$ \frac{\left|{BC}\right|}{\left|{B_{1}C_1}\right|}=\frac{\left|{SB}\right|}{\left|{SB_1}\right|}=\frac{\left|{SC}\right|}{\left|{SC_1}\right|} $$

Таким образом,

$$ \frac{\left|{AB}\right|}{\left|{A_{1}B_1}\right|}=\frac{\left|{BC}\right|}{\left|{B_{1}C_1}\right|}=\frac{\left|{AC}\right|}{\left|{A_{1}C_1}\right|} $$

Соответственные углы треугольников ABC и A1B1C1 конгруэнтны, как углы с параллельными и одинаково направленными сторонами. Поэтому

ΔABC ~ ΔA1B1C1

Площади подобных треугольников относятся, как квадраты соответствующих сторон:

$$ \frac{S_{ABC}}{S_{A_1 B_1 C_1}}=\frac{\left|{AB}\right|^2}{\left|{A_{1}B_1}\right|^2} $$

но

$$ \frac{\left|{AB}\right|}{\left|{A_{1}B_1}\right|}=\frac{\left|{SH}\right|}{\left|{SH_1}\right|} $$

Следовательно,

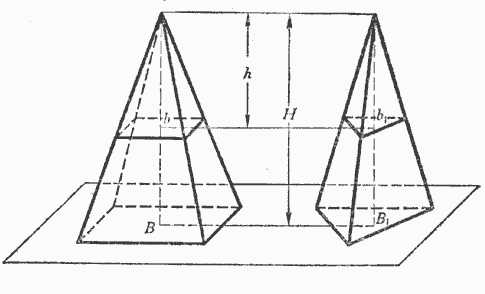
$$ \frac{S_{ABC}}{S_{A_1 B_1 C_1}}=\frac{\left|{SH}\right|^2}{\left|{SH_1}\right|^2} $$

Теорема. Если две пирамиды с равными высотами рассечены на одинаковом расстоянии от вершины плоскостями, параллельными основаниям, то площади сечений пропорциональны площадям оснований.

Пусть (черт. 84) В и В1— площади оснований двух пирамид, H — высота каждой из них, b и b1 — площади сечений плоскостями, параллельными основаниям и удалёнными от вершин на одно и то же расстояние h.

Согласно предыдущей теореме мы будем иметь:

$$ \frac{b}{B}=\frac{h^2}{H^2}\: и \: \frac{b_1}{B_1}=\frac{h^2}{H^2} $$ откуда $$ \frac{b}{B}=\frac{b_1}{B_1}\: или \: \frac{b}{b_1}=\frac{B}{B_1} $$

Следствие. Если В = В1, то и b = b1 , т. е. если у двух пирамид с равными высотами основания равновелики, то равновелики и сечения, равноотстоящие от вершины.

razdupli.ru

Рисунок правильной пирамиды

Чертеж — первый и очень важный шаг в решении геометрической задачи. Каким должен быть рисунок правильной пирамиды?

Сначала вспомним свойства параллельного проектирования:

— параллельные отрезки фигуры изображаются параллельными отрезками;

— сохраняется отношение длин отрезков параллельных прямых и отрезков одной прямой.

Рисунок правильной треугольной пирамиды

Сначала изображаем основание. Поскольку при параллельном проектировании углы и отношения длин не параллельных отрезков не сохраняются, правильный треугольник в основании пирамиды изображается произвольным треугольником.

Центр правильного треугольника — точка пересечения медиан треугольника. Поскольку медианы в точке пересечения делятся в отношении 2:1, считая от вершины, мысленно соединяем вершину основания с серединой противолежащей стороны, приблизительно делим ее на три части, и на расстоянии 2 частей от вершины ставим точку. Из этой точки вверх проводим перпендикуляр. Это — высота пирамиды. Перпендикуляр рисуем такой длины, чтобы боковое ребро не закрывало изображение высоты.

Рисунок правильной четырехугольной пирамиды

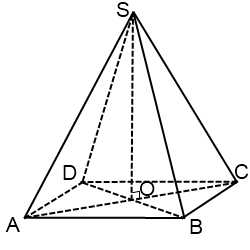
Рисунок правильной четырехугольной пирамиды также начинаем с основания. Поскольку параллельность отрезков сохраняется, а величины углов — нет, то квадрат в основании изображается параллелограммом. Желательно острый угол этого параллелограмма делать поменьше, тогда боковые грани получаются больше. Центр квадрата — точка пересечения его диагоналей. Проводим диагонали, из точки пересечения восстанавливаем перпендикуляр. Этот перпендикуляр — высота пирамиды. Выбираем длину перпендикуляра таким образом, чтобы боковые ребра не сливались между собой.

Рисунок правильной шестиугольной пирамиды

Поскольку при параллельном проектировании параллельность отрезков сохраняется, основание правильной шестиугольной пирамиды — правильный шестиугольник — изображаем шестиугольником, у которого противолежащие стороны параллельны и равны. Центр правильного шестиугольника — точка пересечения его диагоналей. Чтобы не загромождать рисунок, диагонали не проводим, а находим эту точку приблизительно. Из нее восстанавливаем перпендикуляр — высоту пирамиды — так, чтобы боковые ребра не сливались между собой.

www.uznateshe.ru

Пошаговое построение сечения четырехугольной пирамиды

Сегодня научимся строить сечения четырехугольной правильной пирамиды. Использовать для построения будем метод следов. Пользоваться этим методом неудобно и даже иногда невозможно, когда сечение имеет малый наклон или не имеет наклона к плоскости основания. Если такой случай вам попадется, лучше использовать метод внутреннего проецирования.

Задача 1. Построить сечение четырехугольной правильной пирамиды плоскостью, проходящей через точки .

Задача 1. Дано

Шаг 1. Через точки и , принадлежащие плоскости грани , проведем прямую . Определим точку плоскости основания пирамиды, которая бы принадлежала и секущей плоскости. Для этого проведем продолжение ребра и найдем точку его пересечения с прямой – точка .

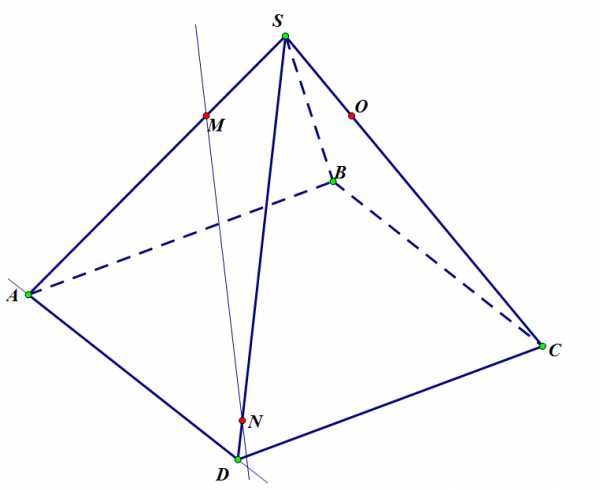
Задача 1. Шаг 1.

Шаг 2. Аналогично найдем вторую точку секущей плоскости в плоскости основания: проводим прямую , находим ее пересечение с продолжением ребра – точка .

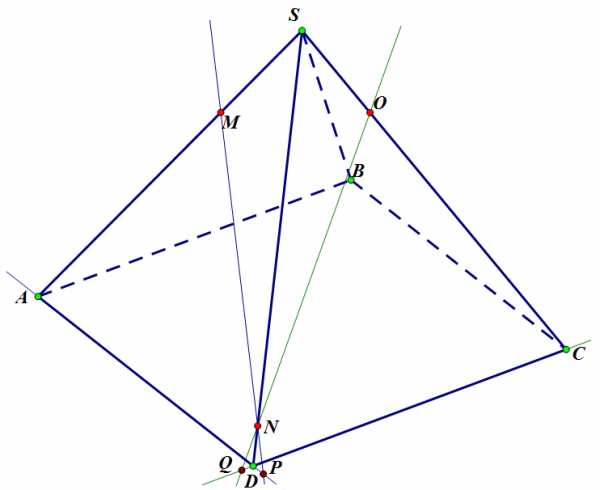
Задача 1. Шаг 2.

Шаг 3. Через две точки можно провести прямую, и, так как точки и принадлежат и секущей плоскости, и плоскости основания, то и прямая, проведенная через них, будет принадлежать обеим плоскостям. А раз эта прямая лежит в плоскости основания, то определим точки пересечения этой прямой с другими прямыми плоскости основания, например, с продолжением ребра – точка , и продолжением ребра – точка . Значит, точки и – тоже точки плоскости сечения, а за счет того, что прямая лежит в плоскости грани , точка также принадлежит плоскости этой грани. Аналогично, так как прямая принадлежит плоскости грани , то и точка – точка этой же плоскости. Теперь можно соединить точки и – как точки одной плоскости, и соединить точки и .

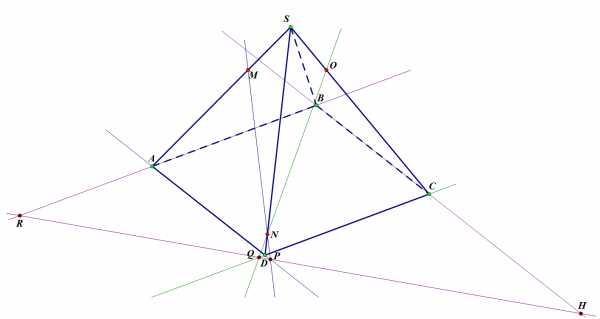
Задача 1. Шаг 3.

Шаг 4. Пересечение прямых и даст нам последнюю точку искомого сечения – точку .

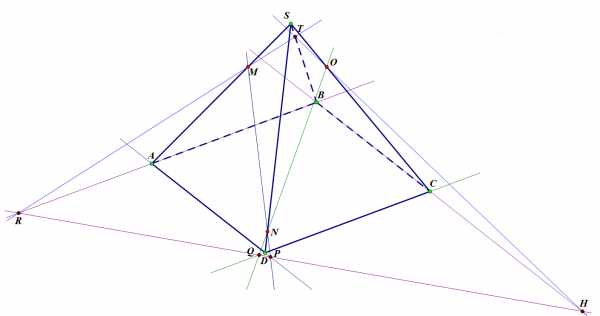
Задача 1. Шаг 4.

Проводим отрезки , , завершая построение:

Многоугольник сечения

Окончательный вид сечения:

Окончательный вид

Задача 2. Построить сечение четырехугольной правильной пирамиды плоскостью, проходящей через точки .

Задача 2. Дано

Шаг 1. Проводим прямую , она принадлежит грани , так как точки и принадлежат ей.

Задача 2. Шаг 1.

Шаг 2. Прямая пересечет прямую , и точка их пересечения благодаря принадлежности прямой будет лежать в плоскости основания.

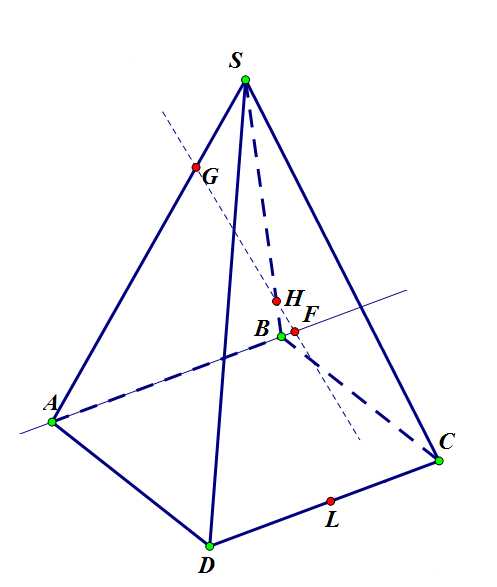
Задача 2. Шаг 2.

Шаг 3. Точки и принадлежат плоскости основания, проведем через них прямую , найдем точку пересечения этой прямой ребра – точку . Продлим прямую до пересечения с прямой , получим точку . Точка принадлежит плоскости , тк как этой плоскости принадлежит прямая .

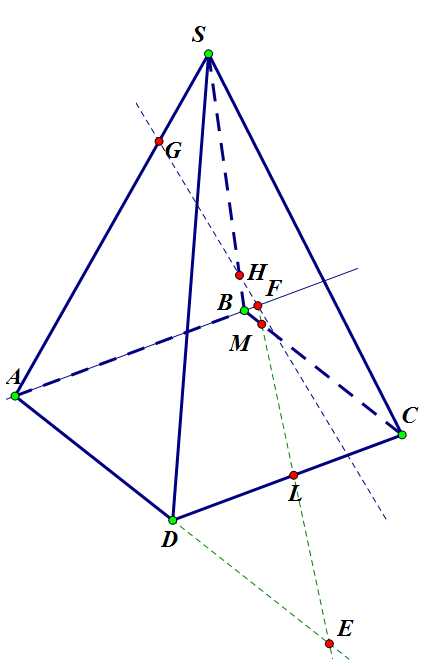
Задача 2. Шаг 3.

Шаг 4. Соединим точки и . Найдем место пересечения данной прямой ребра – точку .

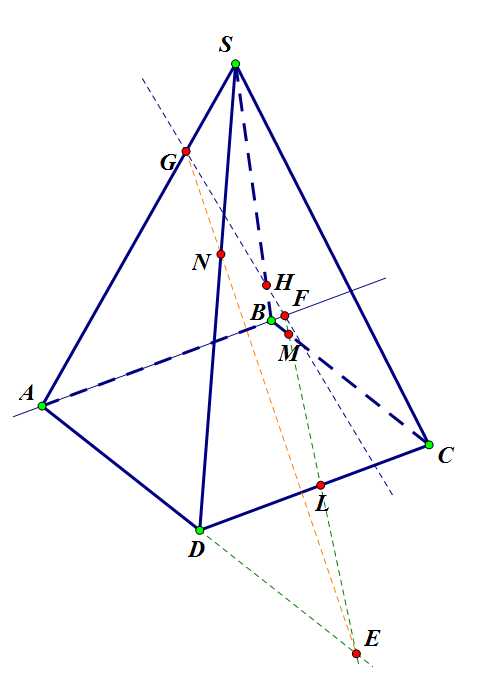
Задача 2. Шаг 4.

Шаг 5. Соединяем полученные точки отрезками.

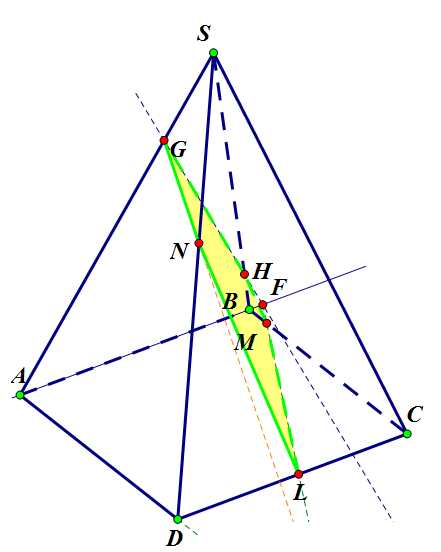
Задача 2. Шаг 5.

Окончательный вид с другого ракурса:

Окончательный вид сечения

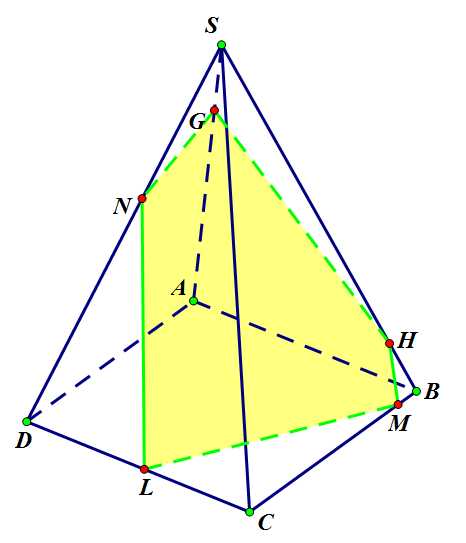
Задача 3. Построить сечение четырехугольной правильной пирамиды плоскостью, проходящей через точки .

Задача 3. Дано

Шаг 1. Соединим и , как точки одной плоскости.

Задача 3. Шаг 1.

Шаг 2. Прямая принадлежит плоскости грани , следовательно, пересечет прямую этой же грани . Найдем точку их пересечения , продлив ребро .

Задача 3. Шаг 2.

Шаг 3. Точки и – “одного поля ягоды” – обе принадлежат плоскости грани . Поэтому соединим их, отметив точку пересечения с ребром – .

Задача 3. Шаг 3.

Шаг 4. Точки и принадлежат плоскости основания, соединяем их. Прямая лежит в плоскости основания и пересечет прямую в точке .

Задача 3. Шаги 4-5.

Шаг 5. Точки и соединяем, так как обе они принадлежат плоскости , и получаем последнюю точку сечения – на ребре .

Шаг 6. Соединяем точки отрезками.

Задача 3. Шаг 6.

Окончательный вид сечения:

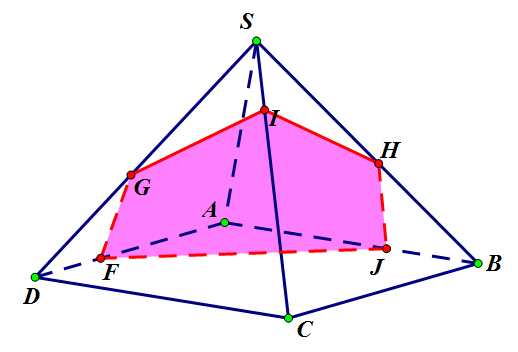
Окончательный вид сечения

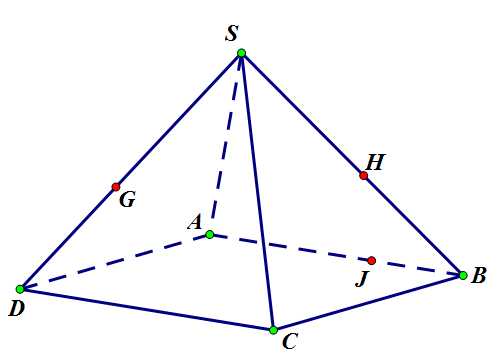
Задача 4. Построить сечение четырехугольной правильной пирамиды плоскостью, проходящей через точки .

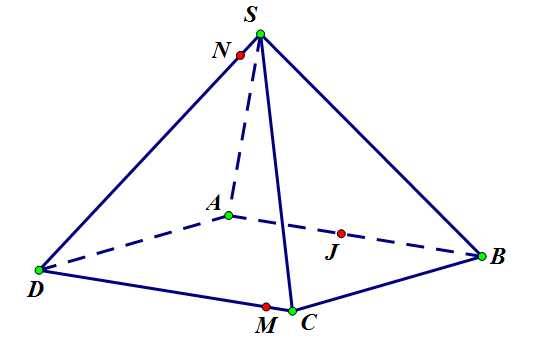
Задача 4. Дано.

Шаг 1-2. Точки и принадлежат грани , соединим их отрезком (прямой). Точки и принадлежат грани основания, также соединим их.

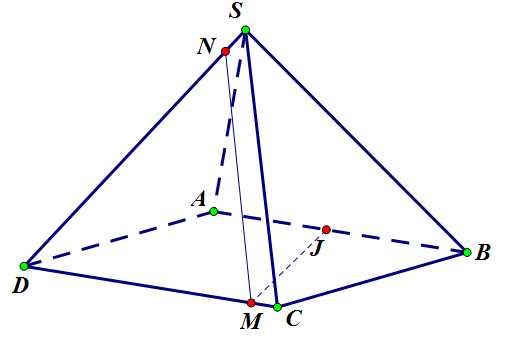
Задача 4. Шаги 1-2

Шаг 3. Прямая пересечет продолжение ребра в точке . Точка , таким образом, принадлежит плоскости грани .

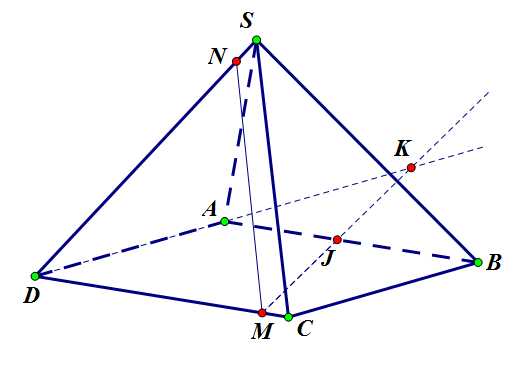
Задача 4. Шаг 3.

Шаг 4. Соединяем точки и , проводя прямую . Она пересечет ребро в точке .

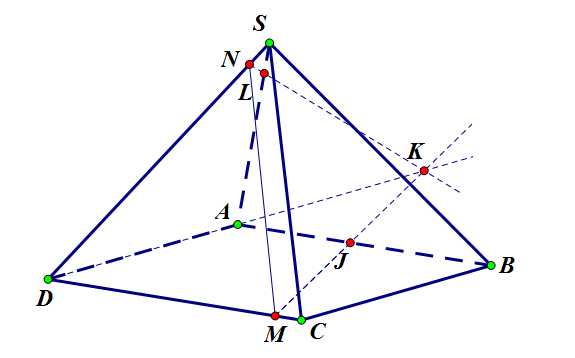
Задача 4. Шаг 4.

Шаг 5. Соединяем полученные точки на ребрах отрезками:

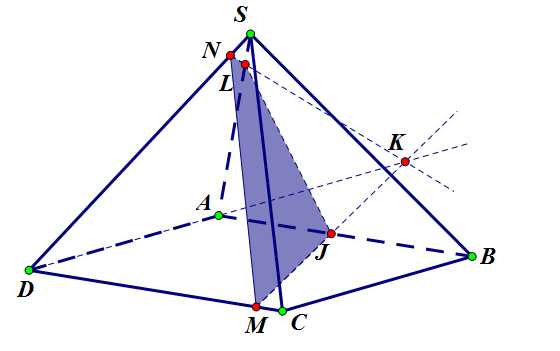
Задача 4. Шаг 5.

Окончательный вид с удобного ракурса:

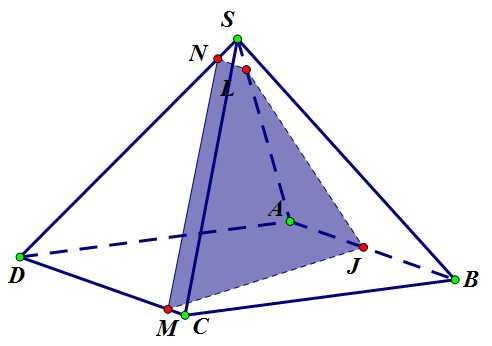
Окончательный вид

easy-physic.ru

Усеченная пирамида

Плоскость, параллельная основанию пирамиды, разбивает исходную пирамиду на две части: пирамиду, подобную данной, и усеченную пирамиду. Усеченная пирамида ограничена основаниями — двумя параллельными подобными многоугольниками, — и боковой поверхностью.

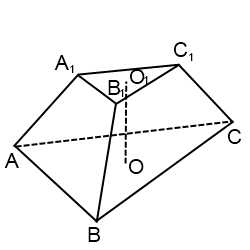
Соответствующие стороны многоугольников в основаниях попарно параллельны, поэтому боковые грани усеченной пирамиды — трапеции.

Высота усеченной пирамиды — это расстояние между плоскостями ее оснований.

Как построить усеченную пирамиду?

Чтобы построить усеченную пирамиду:

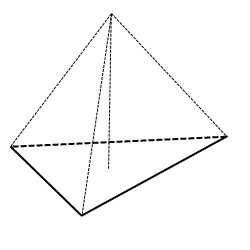
1) строят полную пирамиду;

2) проводят сечение, параллельное основанию;

3) верхнюю часть чертежа стирают.

Объем усеченной пирамиды

Формула объема усеченной пирамиды:

где S1 и S2- площади оснований пирамиды, H — высота пирамиды.

Правильная усеченная пирамида

Усеченная пирамида, полученная из правильной пирамиды, называется правильной усеченной пирамидой. Боковые грани правильной усеченной пирамиды представляют собой равные равнобокие трапеции. Их высоты называют апофемами.

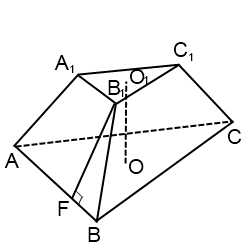
B1F, A1F — апофемы.

Боковая поверхность правильной усеченной пирамиды.

Площадь боковой поверхности правильной усеченной пирамиды может быть найдена по одной из формул:

где P1 и P2 — периметры оснований, l — апофема.

где φ- двугранный угол при большем основании пирамиды.

www.uznateshe.ru

Пирамида. Усеченная пирамида

Пирамидой называется многогранник, одна из граней которого многоугольник (основание), а все остальные грани – треугольники с общей вершиной (боковые грани) (рис. 15). Пирамида называется правильной, если ее основанием является правильный многоугольник и вершина пирамиды проектируется в центр основания (рис. 16). Треугольная пирамида, у которой все ребра равны, называется тетраэдром.

Рис. 15

Рис. 16

Боковым ребром пирамиды называется сторона боковой грани, не принадлежащая основанию Высотой пирамиды называется расстояние от ее вершины до плоскости основания. Все боковые ребра правильной пирамиды равны между собой, все боковые грани – равные равнобедренные треугольники. Высота боковой грани правильной пирамиды, проведенная из вершины, называется апофемой. Диагональным сечением называется сечение пирамиды плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани.

Площадью боковой поверхности пирамиды называется сумма площадей всех боковых граней. Площадью полной поверхности называется сумма площадей всех боковых граней и основания.

Теоремы

1. Если в пирамиде все боковые ребра равнонаклонены к плоскости основания, то вершина пирамиды проектируется в центр окружности описанной около основания.

2. Если в пирамиде все боковые ребра имеют равные длины, то вершина пирамиды проектируется в центр окружности описанной около основания.

3. Если в пирамиде все грани равнонаклонены к плоскости основания, то вершина пирамиды проектируется в центр окружности вписанной в основание.

Для вычисления объема произвольной пирамиды верна формула:

где V – объем;

Sосн – площадь основания;

H – высота пирамиды.

Для правильной пирамиды верны формулы:

где p – периметр основания;

hа – апофема;

H – высота;

Sполн – площадь полной поверхности;

Sбок – площадь боковой поверхности;

Sосн – площадь основания;

V – объем правильной пирамиды.

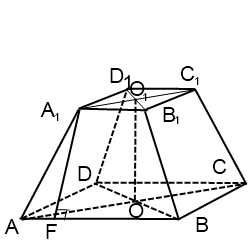
Усеченной пирамидой называется часть пирамиды, заключенная между основанием и секущей плоскостью, параллельной основанию пирамиды (рис. 17). Правильной усеченной пирамидой называется часть правильной пирамиды, заключенная между основанием и секущей плоскостью, параллельной основанию пирамиды.

Основания усеченной пирамиды – подобные многоугольники. Боковые грани – трапеции. Высотой усеченной пирамиды называется расстояние между ее основаниями. Диагональю усеченной пирамиды называется отрезок, соединяющий ее вершины, не лежащие в одной грани. Диагональным сечением называется сечение усеченной пирамиды плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани.

Рис. 17

Для усеченной пирамиды справедливы формулы:

(4)

где S1, S2 – площади верхнего и нижнего оснований;

Sполн – площадь полной поверхности;

Sбок – площадь боковой поверхности;

H – высота;

V – объем усеченной пирамиды.

Для правильной усеченной пирамиды верна формула:

где p1 , p2 – периметры оснований;

hа – апофема правильной усеченной пирамиды.

Пример 1. В правильной треугольной пирамиде двугранный угол при основании равен 60º. Найти тангенс угла наклона бокового ребра к плоскости основания.

Решение. Сделаем рисунок (рис. 18).

Рис. 18

Пирамида правильная, значит в основании равносторонний треугольник и все боковые грани равные равнобедренные треугольники. Двугранный угол при основании – это угол наклона боковой грани пирамиды к плоскости основания. Линейным углом будет угол a между двумя перпендикулярами: и т.е. Вершина пирамиды проектируется в центре треугольника (центр описанной окружности и вписанной окружности в треугольник АВС). Угол наклона бокового ребра (например SB) – это угол между самим ребром и его проекцией на плоскость основания. Для ребра SB этим углом будет угол SBD. Чтобы найти тангенс необходимо знать катеты SO и OB. Пусть длина отрезка BD равна 3а. Точкой О отрезок BD делится на части: и Из находим SO: Из находим:

Ответ:

Пример 2. Найти объем правильной усеченной четырехугольной пирамиды, если диагонали ее оснований равны см и см, а высота 4 см.

Решение. Для нахождения объема усеченной пирамиды воспользуемся формулой (4). Чтобы найти площади оснований необходимо найти стороны квадратов-оснований, зная их диагонали. Стороны оснований равны соответственно 2 см и 8 см. Значит площади оснований и Подставив все данные в формулу, вычислим объем усеченной пирамиды:

Ответ: 112 см3.

Пример 3. Найти площадь боковой грани правильной треугольной усеченной пирамиды, стороны оснований которой равны 10 см и 4 см, а высота пирамиды 2 см.

Решение. Сделаем рисунок (рис. 19).

Рис. 19

Боковая грань данной пирамиды является равнобокая трапеция. Для вычисления площади трапеции необходимо знать основания и высоту. Основания даны по условию, остается неизвестной только высота. Ее найдем из где А1Е перпендикуляр из точки А1 на плоскость нижнего основания, A1D – перпендикуляр из А1 на АС. А1Е = 2 см, так как это высота пирамиды. Для нахождения DE сделаем дополнительно рисунок, на котором изобразим вид сверху (рис. 20). Точка О – проекция центров верхнего и нижнего оснований. так как (см. рис. 20) и С другой стороны ОК – радиус вписанной в окружности и ОМ – радиус вписанной в окружности:

MK = DE.

По теореме Пифагора из

Площадь боковой грани:

Рис. 20

Ответ:

Пример 4. В основании пирамиды лежит равнобокая трапеция, основания которой а и b (a > b). Каждая боковая грань образует с плоскостью основания пирамиды угол равный j. Найти площадь полной поверхности пирамиды.

Решение. Сделаем рисунок (рис. 21). Площадь полной поверхности пирамиды SABCD равна сумме площадей и площади трапеции ABCD.

Воспользуемся утверждением, что если все грани пирамиды равнонаклонены к плоскости основания, то вершина проектируется в центр вписанной в основание окружности. Точка О – проекция вершины S на основание пирамиды. Треугольник SOD является ортогональной проекцией треугольника CSD на плоскость основания. По теореме о площади ортогональной проекции плоской фигуры получим:

Рис. 21

Аналогично и значит Таким образом задача свелась к нахождению площади трапеции АВСD. Изобразим трапецию ABCD отдельно (рис.22). Точка О – центр вписанной в трапецию окружности.

Рис. 22

Так как в трапецию можно вписать окружность, то или Из по теореме Пифагора имеем

Тогда

Площадь трапеции:

Значит,

Ответ:

Пример 5.Основание пирамиды – равносторонний треугольник со стороной а. Одна из боковых граней – равнобедренный прямоугольный треугольник, плоскость которого перпендикулярна плоскости основания. Найти площадь боковой поверхности пирамиды.

Решение. Сделаем рисунок (рис. 23).

Рис. 23

Площадь боковой поверхности данной пирамиды SABC состоит из суммы площадей ее боковых граней. Боковые грани – треугольники, один из которых прямоугольный и равнобедренный ( ), два других – равные треугольники Рассмотрим – по условию. Вычислим его площадь: Так как равнобедренный, то а так как то и следовательно в

Тогда

Рассмотрим SE найдем из По теореме Пифагора имеем Найдем DE. Для этого рассмотрим равносторонний треугольник основания (рис. 24). В отрезок DE является средней линией, значит, Находим SE:

Рис. 24

Теперь

Площадь боковой поверхности пирамиды равна:

Ответ:

Правильная пирамида — урок. Геометрия, 10 класс.

Пирамида, основанием которой является правильный многоугольник, а вершина которой проектируется в центр основания, называется правильной пирамидой.

Боковые грани правильной пирамиды — равные равнобедренные треугольники.

Высота боковой грани правильной пирамиды называется апофемой.

Правильная треугольная пирамида, у которой все рёбра равны, называется тетраэдром.

Все грани тетраэдра — равные равносторонние треугольники.

В средней школе нужно уметь решать задачи, где дана

- правильная треугольная пирамида;

- правильная четырёхугольная пирамида;

- правильная шестиугольная пирамида.

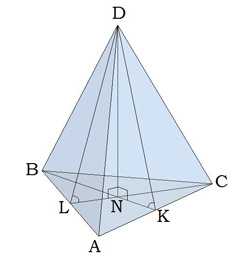
Правильная треугольная пирамида

Основание правильной треугольной пирамиды — равносторонний треугольник.

Вершина пирамиды проектируется в точку пересечения медиан.

Запомни:

$BN:NK = 2:1$

$KD$ — апофема,

&angsph;$NKD$ и &angsph;$NLD$ — двугранные углы при основании пирамиды,

&angsph;$DCN$и &angsph;$DBN$ — углы между боковым ребром и плоскостью основания пирамиды.

Правильная четырёхугольная пирамида

Основание правильной четырёхугольной пирамиды — квадрат.

Вершина пирамиды проектируется в точку пересечения диагоналей основания (квадрата).

$ML$ — апофема,

&angsph;$MLO$ — двугранный угол при основании пирамиды,

&angsph;$MCO$ — угол между боковым ребром и плоскостью основания пирамиды.

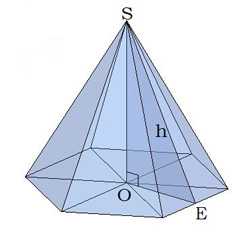
Правильная шестиугольная пирамида

Основание правильной шестиугольной пирамиды — правильный шестиугольник.

Вершина пирамиды проектируется в точку пересечения диагоналей основания (шестиугольника).

$SE = h$ — апофема,

&angsph;$OES$ — двугранный угол при основании пирамиды.

Для вычисления площади боковой поверхности правильной пирамиды существуют две формулы:

Sб=12Pоснования⋅hиSб=Sоснованияcosϕ, где $P$ — периметр основания, $h$ — апофема, ϕ — двугранный угол при основании.

Объём пирамиды $V =$13Sосн⋅H, где $H$ — высота пирамиды.

Обрати внимание!

Не путай $h$ — апофему с $H$ — высотой пирамиды!

www.yaklass.ru

Задачи на усеченную пирамиду

Многогранник, у которого одна из граней – многоугольник, а все остальные грани – треугольники с общей вершиной, называется пирамидой.

Эти треугольники, из которых составлена пирамида, называют боковыми гранями, а оставшийся многоугольник – основанием пирамиды.

В основании пирамиды лежит геометрическая фигура – n-угольник. В таком случае пирамиду называют еще n-угольной.

Треугольную пирамиду, все ребра которой равны, называют тетраэдром.

Ребра пирамиды, которые не принадлежат основанию, называются боковыми, а их общая точка – это вершина пирамиды. Другие ребра пирамиды обычно называют сторонами основания.

Пирамиду называют правильной, если у нее в основании лежит правильный многоугольник, а все боковые ребра равны между собой.

Расстояние от вершины пирамиды до плоскости основания называется высотой пирамиды. Можно сказать, что высота пирамиды есть отрезок, перпендикулярный основанию, концы которого находятся в вершине пирамиды и на плоскости основания.

Для любой пирамиды имеют место следующие формулы:

1) Sполн = S бок + Sосн, где

Sполн – площадь полной поверхности пирамиды;

Sбок – площадь боковой поверхности, т.е. сумма площадей всех боковых граней пирамиды;

S осн – площадь основания пирамиды.

2) V = 1/3 Sосн · Н, где

V – объем пирамиды;

Н – высота пирамиды.

Для правильной пирамиды имеет место:

Sбок = 1/2 Pосн h, где

Pосн – периметр основания пирамиды;

h – длина апофемы, то есть длина высоты боковой грани, опущенной из вершины пирамиды.

Часть пирамиды, заключенная между двумя плоскостями – плоскостью основания и секущей плоскостью, проведенной параллельно основанию, называют усеченной пирамидой.

Основание пирамиды и сечение пирамиды параллельной плоскостью называются основаниями усеченной пирамиды. Остальные грани называют боковыми. Расстояние между плоскостями оснований называют высотой усеченной пирамиды. Ребра, которые не принадлежат основаниям, называются боковыми.

Кроме того, основания усеченной пирамиды подобные n-угольники. Если основания усеченной пирамиды – правильные многоугольники, а все боковые ребра равны между собой, то такая усеченная пирамида называется правильной.

Для произвольной усеченной пирамиды имеют место следующие формулы:

1) Sполн = Sбок + S1 + S2, где

Sполн – площадь полной поверхности;

Sбок – площадь боковой поверхности, т.е. сумма площадей всех боковых граней усеченной пирамиды, которые представляют собой трапеции;

S1, S2 – площади оснований;

2) V = 1/3( S1 + S2 + √(S1 · S2 ))H, где

V – объем усеченной пирамиды;

H – высота усеченной пирамиды.

Для правильной усеченной пирамиды также имеем:

Sбок = 1/2(P1 + P2) · h, где

P1 , P2 – периметры оснований;

h – апофема (высота боковой грани, представляющей собой трапецию).

Рассмотрим несколько задач на усеченную пирамиду.

Задача 1.

В треугольной усеченной пирамиде с высотой, равной 10, стороны одного из оснований равны 27, 29 и 52. Определите объем усеченной пирамиды, если периметр другого основания равен 72.

Решение.

Рассмотрим усеченную пирамиду АВСА1В1С1, изображенную на рисунке1.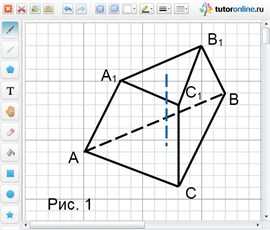

1. Объем усеченной пирамиды может быть найден по формуле

V = 1/3H · (S1 + S2 + √(S1 · S2)), где S1 – площадь одного из оснований, можно найти по формуле Герона

S = √(p(p – a)(p – b)(p – c)),

т.к. в задаче даны длины трех сторон треугольника.

Имеем: p1 = (27 + 29 + 52)/2 = 54.

S1 = √(54(54 – 27)(54 – 29)(54 – 52)) = √(54 · 27 · 25 · 2) = 270.

2. Пирамида усеченная, а значит, в основаниях лежат подобные многоугольники. В нашем случае треугольник АВС подобен треугольнику А1В1С1. Кроме того, коэффициент подобия можно найти как отношение периметров рассматриваемых треугольников, а отношение их площадей будет равно квадрату коэффициента подобия. Таким образом, имеем:

S1/S2 = (P1)2/(P2)2 = 1082/722 = 9/4. Отсюда S2 = 4S1/9 = 4 · 270/9 = 120.

Итак, V = 1/3 · 10(270 + 120 + √(270 · 120)) = 1900.

Ответ: 1900.

Задача 2.

В треугольной усеченной пирамиде через сторону верхнего основания проведена плоскость параллельно противоположному боковому ребру. В каком отношении разделился объем усеченной пирамиды, если соответственные стороны оснований относятся как 1 : 2?

Решение.

Рассмотрим АВСА1В1С1 – усеченную пирамиду, изображенную на рис. 2.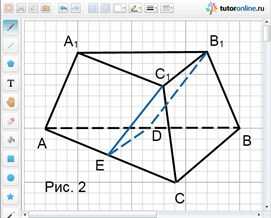

Так как в основаниях стороны относятся как 1 : 2, то площади оснований относятся как 1 : 4 (треугольник АВС подобен треугольнику А1В1С1).

Тогда объем усеченной пирамиды равен:

V = 1/3h · (S1 + S2 + √(S1 · S2)) = 1/3h · (4S2 + S2 + 2S2) = 7/3 · h · S2, где S2 – площадь верхнего основания, h – высота.

Но объем призмы АDEA1B1C1 составляет V1 = S2 · h и, значит,

V2 = V – V1 = 7/3 · h · S2 - h · S2 = 4/3 · h · S2.

Итак, V2 : V1 = 3 : 4.

Ответ: 3 : 4.

Задача 3.

Стороны оснований правильной четырехугольной усеченной пирамиды равны 2 и 1, а высота равна 3. Через точку пересечения диагоналей пирамиды параллельно основаниям пирамиды проведена плоскость, делящая пирамиду на две части. Найти объем каждой из них.

Решение.

Рассмотрим усеченную пирамиду АВСDА1В1С1D1, изображенную на рис. 3.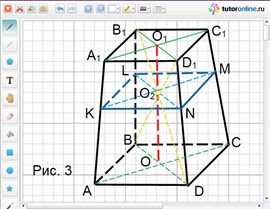

Обозначим О1О2 = х, тогда ОО₂ = О1О – О1О2 = 3 – х.

Рассмотрим треугольник В1О2D1 и треугольник ВО2D:

угол В1О2D1 равен углу ВО2D как вертикальные;

угол ВDO2 равен углу D1B1O2 и угол O2ВD равен углу B1D1O2 как накрест лежащие при B1D1 || BD и секущих B₁D и BD₁ соответственно.

Следовательно, треугольник В1О2D1 подобен треугольнику ВО2D и имеет место отношение сторон:

В1D1/ВD = О1О2/ОО2 или 1/2 = х/(х – 3), откуда х = 1.

Рассмотрим треугольник В1D1В и треугольник LО2B: угол В – общий, а так же имеется пара односторонних углов при B1D1 || LM, значит, треугольник В1D1В подобен треугольнику LО2B, откуда В1D : LO2 = OO1 : OO2 = 3 : 2, т.е.

LO2 = 2/3 · B1D1, LN = 4/3 · B1D1.

Тогда SKLMN = 16/9 · SA1B1C1D1 = 16/9.

Итак, V1 = 1/3 · 2(4 + 16/9 + 8/3) = 152/27.

V2 = 1/3 · 1 · (16/9 + 1 + 4/3) = 37/27.

Ответ: 152/27; 37/27.

blog.tutoronline.ru

Пирамида и усеченная пирамида. Изобразите усеченную четырехугольную пирамиду