Содержание
Как найти Объем Параллелепипеда?
Понятие объема
Чтобы без труда вычислить объём любой фигуры, нужно разобраться с определениями.
Объём — это количественная характеристика пространства, занимаемого телом или веществом.
Другими словами, это то, сколько места занимает предмет.
Объём измеряется в единицах измерения размера пространства, занимаемого телом, то есть в кубических метрах, кубических сантиметрах, кубических миллиметрах.
За единицу измерения объёма можно принять куб с ребром 1 см, то есть, кубический сантиметр (см3), кубический миллиметр (1 мм3), кубический метр (1 м3).
Объём всегда выражается в положительных числах. Это число показывает, какое именно количество единиц измерения есть в теле. Например, сколько воды в бассейне, сока в графине, земли в клумбе.
Два свойства объёма
|
Любое объемное тело имеет объем. Получается, при желании мы можем вычислить объем кружки, смартфона, вазы, кота — чего угодно.
Демо урок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
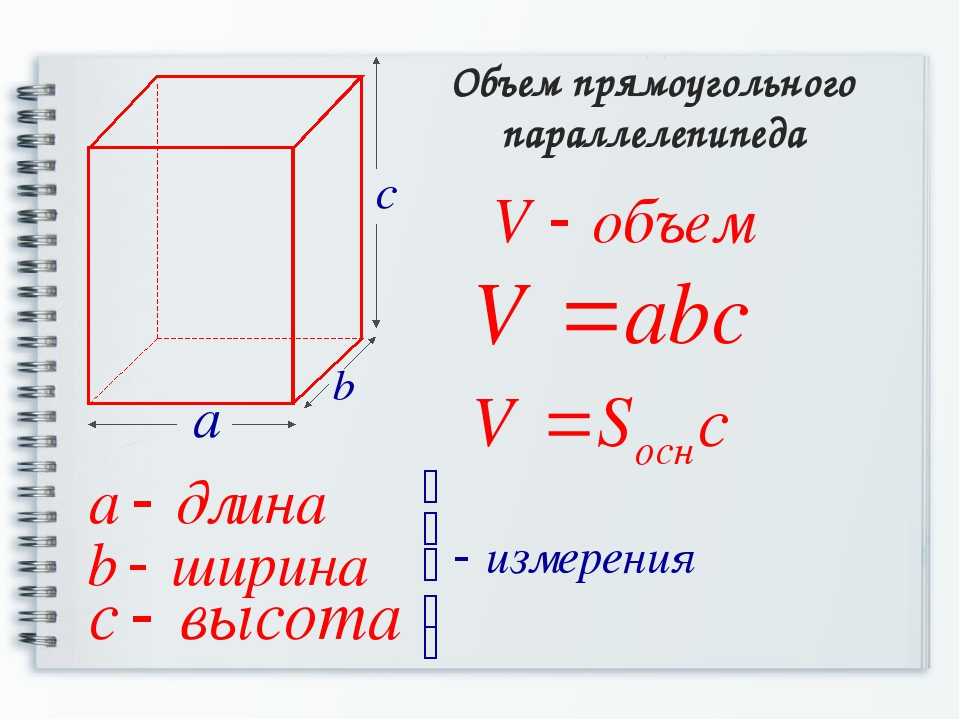
Объем прямоугольного параллелепипеда
Параллелепипед — это многогранник с шестью гранями, каждая из которых является параллелограммом.
Прямоугольным параллелепипедом называют параллелепипед, у которого все грани являются прямоугольниками.
Формула объема прямоугольного параллелепипеда Чтобы вычислить объем прямоугольного параллелепипеда, найдите произведение его длины, ширины и высоты: V = a × b × h |
Чтобы не запутаться в формулах, запоминайте табличку с условными обозначениями.
a | длина параллелепипеда |
b | ширина параллелепипеда |
h | высота параллелепипеда |
P (осн) | периметр основания |
S (осн) | площадь основания |
S (бок) | площадь боковой поверхности |
S (п.п.) | площадь полной поверхности |
V | объем |
Пример 1. Чему равен объем параллелепипеда со сторонами 9 см, 6 см, 3 см.
Чему равен объем параллелепипеда со сторонами 9 см, 6 см, 3 см.
a = 9 см
b = 6 см
h = 3 см
V = a × b × h
V = 9 × 6 × 3 = 162 см3.
Ответ: объем прямоугольного параллелепипеда равен 162 см3.
Следствие Объем параллелепипеда равен произведению площади основания на высоту. V = Sосн × h |
Из этого следствия выведем формулу нахождения площади основания параллелепипеда.
Sосн = V : h
Пример 2. Найдите площадь основания параллелепипеда, если его объем равен 96 см3, а высота 8 см.
V = 96 см3
h = 8 см
V = Sосн × h
Sосн = V : h
Sосн = 82 см3 : 8 см = 12 см2.
Ответ: площадь основания параллелепипеда равна 12 см2.
Обучение на курсах по математике в онлайн-школе Skysmart поможет быстрее разобраться в теме и правильно решать задачки!
Вычисление площади
Как вы уже поняли, вычисление объёма параллелепипеда напрямую зависит от вычисления его площади. Давайте разберемся, сколько всего площадей можно найти в параллелепипеде.
Чтобы найти площадь боковой поверхности параллелепипеда, вычислите по отдельности площадь каждой боковой грани, а затем найдите сумму получившихся значений.
Так как противолежащие грани прямоугольного параллелепипеда одинаковые, то получим формулу:
- Sб. п. = 2 (ac + bc)
Чтобы вычислить площадь полной поверхности параллелепипеда, сложите площадь боковой поверхности и две площади основания. Так как площади оснований у прямоугольного параллелепипеда одинаковые, то получим формулу:
- Sп.
 п. = 2 (ab + ac + bc)
п. = 2 (ab + ac + bc)
Пример 3. Найдем площадь поверхности параллелепипеда, если длина основания равна 6 сантиметров, ширина — 4 см соответственно, а высота — 3 см.
Sп. п. = 2 (ab + ac + bc)
Sп. п. = 2 (6 × 4 + 6 × 3 + 4 × 3) = 2 × (24 + 18 + 12) = 2 × 54 = 108 см2.
Ответ: площадь поверхности параллелепипеда — 108 см2.
Как видите, вычислить объём и найти площадь параллелепипеда совсем не трудно.
Задачи на самопроверку
Пользоваться онлайн-калькуляторами можно, когда вы уже натренировались в решении задачек и с закрытыми глазами можете вычислить объем любого параллелепипеда. Давайте разберем еще несколько примеров.
Задачка 1. Найдите объём параллелепипеда со сторонами 18 см, 10 см, 7 см.
Как решаем:
a = 18 см
b = 10 см
h = 7 см
Формула нахождения объема параллелепипеда:
V = a × b × h
Подставляем наши числа:
V = 18 × 10 × 7 = 1260 см3.
Ответ: объём параллелепипеда равен 1260 см3.
Задачка 2. Найдите площадь основания параллелепипеда, если его объём равен 120 см3, а высота — 15 см.
Как решаем:
V = 120 см
h = 15 см
V = Sосн × h
Sосн = V : h
Sосн = 120 см3: 15 см = 8 см2.
Ответ: площадь основания параллелепипеда равна 8 см2.
Задачка 3. Найдите площадь полной поверхности прямоугольного параллелепипеда, если длина основания равна 30 сантиметров, ширина равна 12 см, а высота равна 5 см.
Как решаем:
Sп. п. = 2 (ab + ac + bc)
Sп. п. = 2 (30 × 12 + 30 × 5 + 12 × 5) = 2 × (360 + 150 + 60) = 2 × 570 = 1140 см2.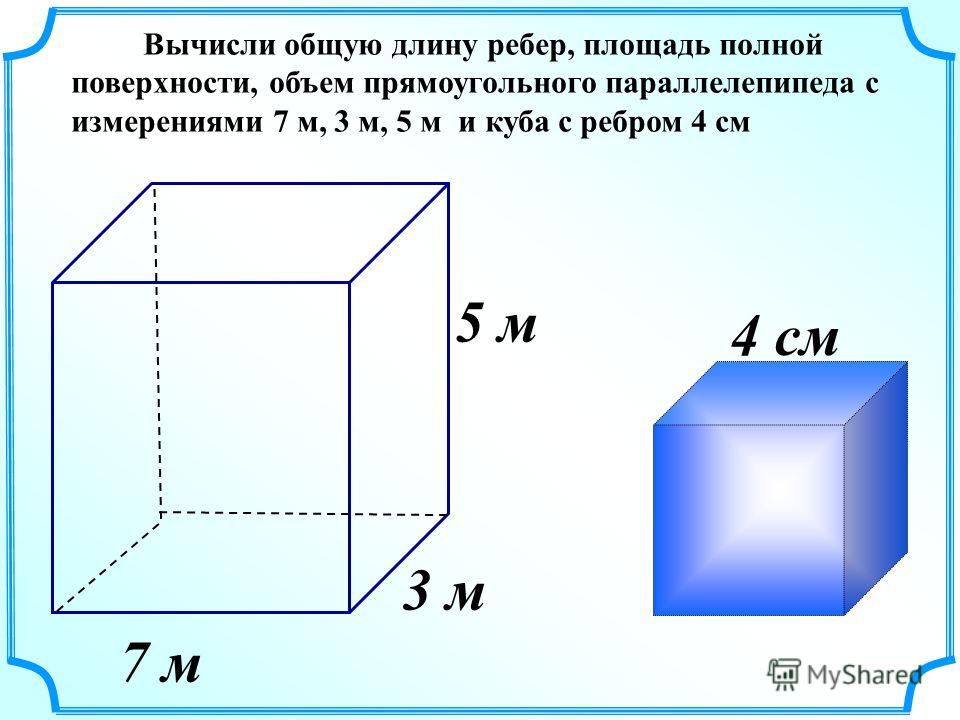
Ответ: площадь полной поверхности параллелепипеда равна 1140 см2.
Пусть все необходимые формулы будут под рукой в нужный момент. Сохраняйте табличку-шпаргалку на гаджет или распечатайте ее и храните в учебнике.
V параллелепипеда | V = a × b × h |
| V = Sосн × h |
S боковой поверхности | Sб. п. = 2 (ac + bc) |
S полной поверхности | Sп. п. = 2 (ab + ac + bc) |
формула через диаметр и высоту
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel. ru Математика Геометрия Нахождение объема цилиндра: формула и задачи
ru Математика Геометрия Нахождение объема цилиндра: формула и задачи
В данной публикации мы рассмотрим, как можно найти объем цилиндра и разберем примеры решения задач.
- Формула вычисления объема цилиндра
- Через площадь основания и высоту
- Через радиус основания и высоту
- Через диаметр основания и высоту
- Примеры задач
Формула вычисления объема цилиндра
Через площадь основания и высоту
Объем (V) цилиндра равняется произведению его высоты и площади основания.
V = S ⋅ H
Через радиус основания и высоту
Как мы знаем, в качестве оснований цилиндра (равны между собой) выступает круг, площадь которого вычисляется так: S = π ⋅ R2. Следовательно, формулу для вычисления объема цилиндра можно представить в виде:
V = π ⋅ R2 ⋅ H
Примечание: в расчетах значение числа π округляется до 3,14.
Через диаметр основания и высоту
Как нам известно, диаметр круга равняется двум его радиусам: d = 2R. А значит, вычислить объем цилиндра можно следующим образом:
V = π ⋅ (d/2)2 ⋅ H
Примеры задач
Задание 1
Найдите объем цилиндра, если дана площадь его основания – 78,5 см2, а также, высота – 10 см.
Решение:
Применим первую формулу, подставив в нее известные значения:
V = 78,5 см2 ⋅ 10 см = 785 см3.
Задание 2
Высота цилиндра равна 6 см, а его диаметр – 8 см. Найдите объем фигуры.
Решение:
Воспользовавшись третьей формулой, в которой участвует диаметр, получаем:
V = 3,14 ⋅ (8/2 см)2 ⋅ 6 см = 301,44 см3.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Что такое объем? Значение, определение, формула, примеры, расчет
Что такое
Объем ?
Каждый трехмерный объект занимает некоторое пространство. Это пространство измеряется с точки зрения его объема. Объем определяется как пространство, занимаемое в границах объекта в трехмерном пространстве. Он также известен как мощность объекта.
Это пространство измеряется с точки зрения его объема. Объем определяется как пространство, занимаемое в границах объекта в трехмерном пространстве. Он также известен как мощность объекта.
Нахождение объема объекта может помочь нам определить объем, необходимый для заполнения этого объекта, например количество воды, необходимое для заполнения бутылки, аквариума или резервуара для воды.
Объем трехмерных фигур:
Поскольку разные трехмерные объекты имеют разную форму, их объемы также различны. Давайте посмотрим на некоторые трехмерные фигуры и научимся вычислять их объем (V).
Сфера
Самый простой и распространенный тип трехмерной формы — это сфера. Некоторые примеры сфер, которые мы видим в повседневной жизни, включают шары, глобусы, декоративные светильники, апельсины и т. д. Самое простое измерение, которое можно сделать на сфере, — это ее радиус. Объем сферы вычисляется по ее радиусу.
Объем сферы = $\frac{4}{3}$ πr 3 , где r — радиус сферы.
Куб
Следующая простая и распространенная трехмерная фигура — куб. Он определяется тем уникальным свойством, что каждая сторона куба имеет одинаковую длину. Некоторыми повседневными примерами предметов в форме куба являются игральные кости, кубики Рубика, кубики сахара, подарочные коробки и т. д. Объем куба рассчитывается по длине его стороны.
Объем куба = a 3 , , где a — длина каждой стороны куба.
Прямоугольная форма
Прямоугольная призма. В прямоугольном параллелепипеде длина сторон будет разной. Следующие обозначения используются для обозначения сторон прямоугольного параллелепипеда.
- Длина = л
- Ширина = b
- Высота = ч
Все эти размеры используются для расчета объема прямоугольного параллелепипеда. Типичными примерами кубоидов являются книги, обувные коробки, кирпичи, матрацы и т. д.
д.
Объем кубоида = l x b x h
Цилиндр
Цилиндр также представляет собой трехмерную форму с круглым основанием и высотой разделение двух оснований. К повседневным цилиндрическим предметам относятся бутылки с водой, ведра, свечи, банки и т. д. Объем цилиндра рассчитывается путем измерения радиуса основания и высоты.
Объем цилиндра = πr 2 H , , где R — Radius базы, а H — это высота R — это Radius базовой и H . .
Конус
Конус — это трехмерная форма, которую мы обычно видим вокруг себя. Рожок для мороженого, праздничная шляпа, воронка или рождественская елка — все это примеры конуса. Конус представляет собой характерную трехмерную геометрическую фигуру, которая имеет плоскую поверхность и криволинейную поверхность, направленную вверх.
Объем конуса = $\frac{1}{3}$πr 2 h, где r — радиус основания конуса, а h — высота конуса из основание к вершине.
Измерение объема
Объем рассчитывается для трехмерных объектов и поэтому представляется в кубических единицах или в другом формате записи кубических единиц; так как это обычно используется (единица измерения)³, например, кубические сантиметры, кубический дюйм, кубический фут, кубический метр и т. д. Если длина или радиус измеряются в сантиметрах, то объем измеряется в кубических сантиметрах (см 3 ). Если размеры указаны в метрах, объем измеряется в кубических метрах (м 3 ).
Когда мы измеряем объем жидкости (например, чтобы найти объем воды, который может вместить цилиндрическая бутылка), мы должны изменить значения в см 3 или м 3 на литры. Объем можно перевести из литров в сантиметры по следующей формуле.
1 л = 1000 см 3
1 l = 1000 ml
1000 cm 3 = 1000 ml
So, 1 см 3 = 1 мл
Заключение
Понимание математических понятий, таких как объем, становится интересным с помощью наглядных пособий, таких как интерактивные игры. Вы можете проверить игры, рабочие листы и решенные задачи по темам, подобным этой, на веб-сайте Splashlearn. Посетите https://www.splashlearn.com/, чтобы узнать новые концепции, развлекаясь.
Вы можете проверить игры, рабочие листы и решенные задачи по темам, подобным этой, на веб-сайте Splashlearn. Посетите https://www.splashlearn.com/, чтобы узнать новые концепции, развлекаясь.
Решенные примеры
1. У Генри есть цилиндрическая бутылка для воды с радиусом основания 5 см и высотой 10 см. Какой объем воды может храниться в бутылке?
Решение:
Том бутылки = πr 2 H
= π (5 x 5) x 10
= π x 250
= 3,14 x 250233333339
= 3,14 x 25023333333339
= 3,14 x 25023333333339
= 3,14 x 25023333333339
= 3,14 x 25023333333339
.
= 785 см 3
= 785 мл (1 см 3 = 1 мл)
2. Риаз владеет мячом для крикета радиусом 3 см. Какой объем занимает мяч в сумке Риаза?
Решение:
Объем шара = $\frac{4}{3}$ πr 3
= $\frac{4}{3}$ x $\frac{22 {7}$ x (3 x 3 x 3)
= 113,14 см 3
3. Коническая новогодняя елка изготовлена из глины. Высота дерева 14 дюймов, а диаметр основания 6 дюймов. Сколько глины используется? (используйте π = $\frac{22}{7}$)
Коническая новогодняя елка изготовлена из глины. Высота дерева 14 дюймов, а диаметр основания 6 дюймов. Сколько глины используется? (используйте π = $\frac{22}{7}$)
Решение:
Диаметр = 6 дюймов
Радиус = $\frac{6}{2}$ = 3 дюйма
Объем глина = $\frac{1}{3}$ πr 2 h
= $\frac{1}{3}\times \frac{22}{7}\times 3\times 3\times 14
$
= 132 кубических дюйма.
Практические задачи
1
Какая из следующих формул является формулой объема книги с размерами l, b и h?
l x l x l
b x b x b
h x h x h
l x b x h
Правильный ответ: l x b x h
Книга представляет собой прямоугольный параллелепипед, объем которого вычисляется по формуле l x b x h.
2
По какой формуле можно рассчитать объем дорожного конуса высотой 20 см и радиусом основания 10 см?
$\frac{4}{3}\pi$ (10 x 10) x 20
$\pi$ (10 x 10) x 20
$\frac{1}{3}\pi$ (10 х 10) х 20
$\frac{2}{3}\pi$ (10 х 10) х 20 9{3}$
Часто задаваемые вопросы
Является ли объем прямоугольной призмы таким же, как объем параллелепипеда?
Да, объем прямоугольной призмы такой же, как объем параллелепипеда.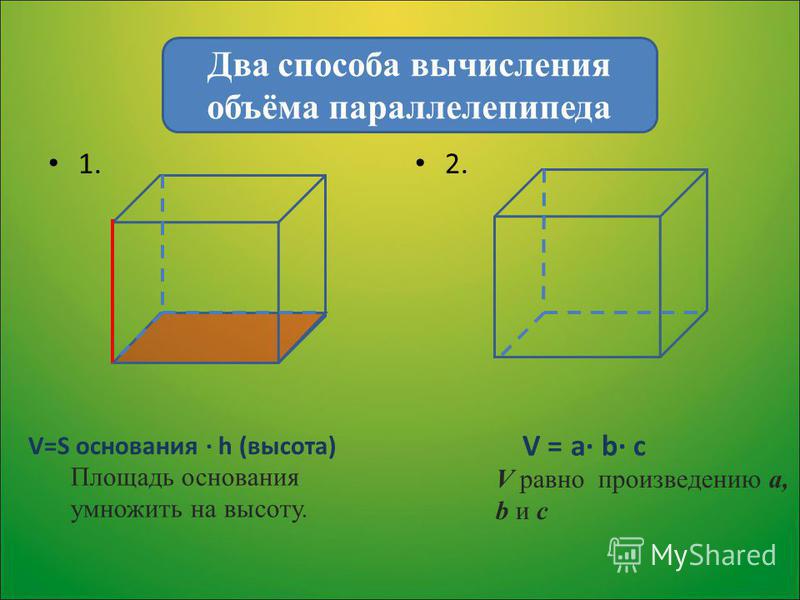 Кубоид имеет стороны неравной длины. Его объем рассчитывается по формуле л x b x h , где л, b и h — это различные измерения формы.
Кубоид имеет стороны неравной длины. Его объем рассчитывается по формуле л x b x h , где л, b и h — это различные измерения формы.
Как рассчитать объем неправильной формы?
Если вам нужно рассчитать объем фигуры, которая не является одной из правильных трехмерных фигур, разбейте неправильную форму на разные правильные формы. Добавьте отдельные объемы этих фигур, чтобы получить общий объем.
Как проще всего определить громкость?
Объем — это пространство, занимаемое любым объектом. Это занимаемое пространство зависит от формы объекта. Лучший способ понять — исследовать различные предметы и найти объем, занимаемый ими.
Что следует учитывать при расчете объемов различной формы?
Важной проверкой перед расчетом объема любой формы должно быть то, что все измерения должны быть в одних и тех же единицах измерения. Если одно измерение указано в см, а другое в м, перед расчетом объема конвертируйте оба значения в см или м.
Объем – формула, определение, расчет, примеры
Объем – это мера емкости, которую содержит объект. Например, если чашка может вместить до краев 100 мл воды, говорят, что ее объем равен 100 мл. Объем также можно определить как объем пространства, занимаемый трехмерным объектом. Объем твердого тела, такого как куб или прямоугольный параллелепипед, измеряется путем подсчета количества содержащихся в нем единичных кубов. Лучший способ визуализировать объем — думать о нем с точки зрения пространства, заключенного/занятого любым трехмерным объектом или твердой формой. В этом можно убедиться с помощью простого упражнения дома:
- Возьмите прямоугольный лист бумаги длиной ‘ l ‘ см и шириной ‘ h ‘ см.
- Соедините противоположные стороны листа бумаги, не сгибая лист.
- Вы создали трехмерный объект, заключающий внутри себя пространство, из двухмерного листа.
1. | Определение тома |
| 2. | Объем трехмерных фигур |
| 3. | Список формул объема |
| 4. | Как рассчитать объем? |
| 5. | Единицы объема |
| 6. | Калькулятор объема |
| 7. | Часто задаваемые вопросы по тому |
Определение тома
Объем определяется как объем, занимаемый трехмерной твердой формой. В любой форме это трудно визуализировать, но можно сравнить между формами. Например, объем ящика компаса больше объема помещенного в него ластика. Для вычисления площади любой двумерной фигуры мы делим часть на равные квадратные единицы. Точно так же при вычислении объема объемных фигур мы будем делить его на равные кубические единицы. Давайте узнаем, как рассчитать объем различных твердых фигур в нашем следующем разделе.
Объем 3D-фигур
Каждый предмет в нашем окружении имеет свойство занимать пространство.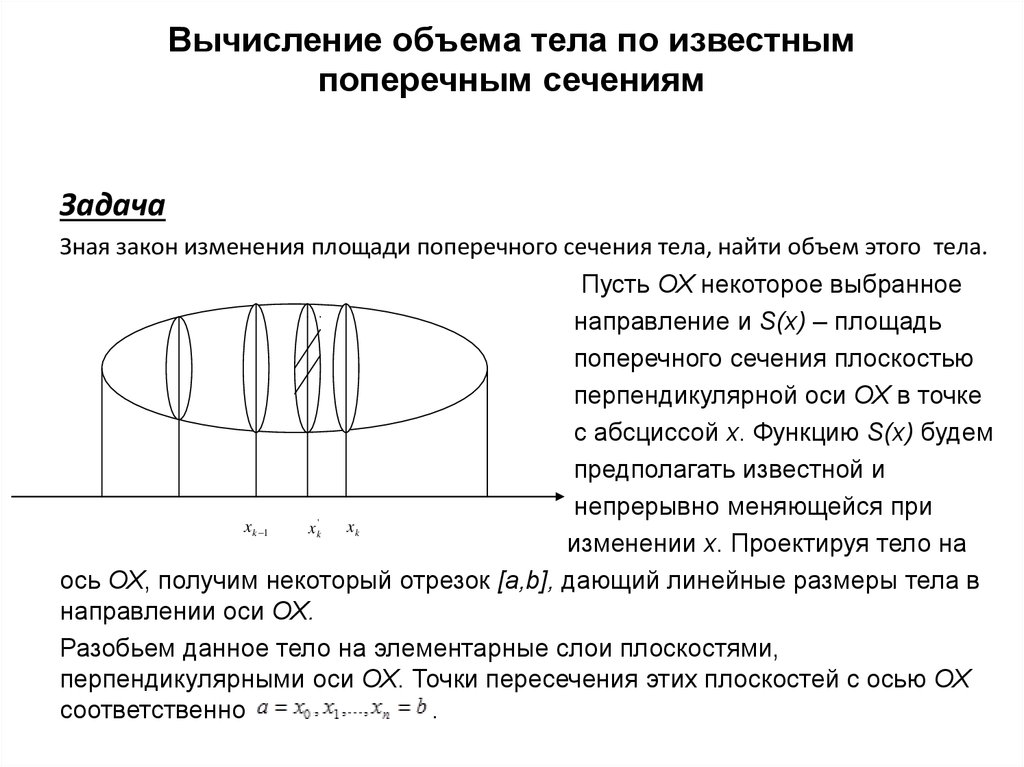 Эти реальные объекты можно легко сравнить с основными трехмерными формами. Давайте посмотрим на объем этих твердых фигур в деталях.
Эти реальные объекты можно легко сравнить с основными трехмерными формами. Давайте посмотрим на объем этих твердых фигур в деталях.
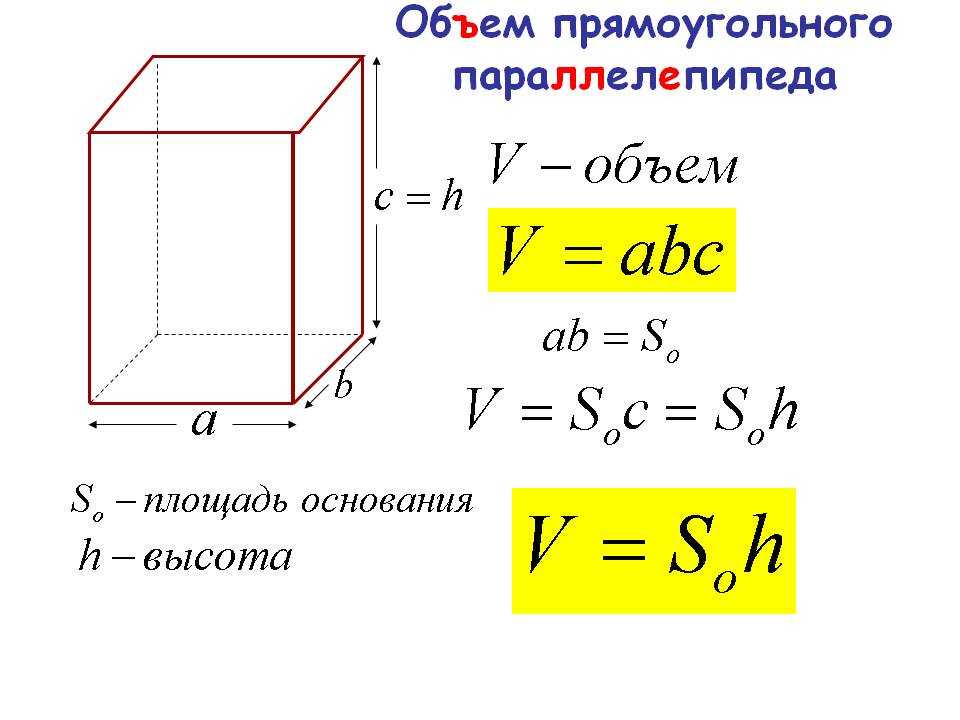
Объем кубоида
Предположим, у нас есть несколько прямоугольных листов длиной ‘l’ и шириной ‘ b’ . Если мы сложим их один поверх другого до высоты ‘h’ , мы получим прямоугольный параллелепипед размерности л, б, з . Это можно увидеть на следующем рисунке, на котором показаны длина, ширина (ширина) и высота образованного таким образом прямоугольного параллелепипеда.
Чтобы вычислить объем пространства, заключенного в этот прямоугольный параллелепипед, мы используем формулу: Объем прямоугольного параллелепипеда = l × b × h
Объем кубоида
Куб является частным случаем прямоугольного параллелепипеда, где все три стороны равны по мере. Если мы представим это равное значение как «а», то объем этого куба можно будет рассчитать по формуле: Объем куба = а × а × а = а³.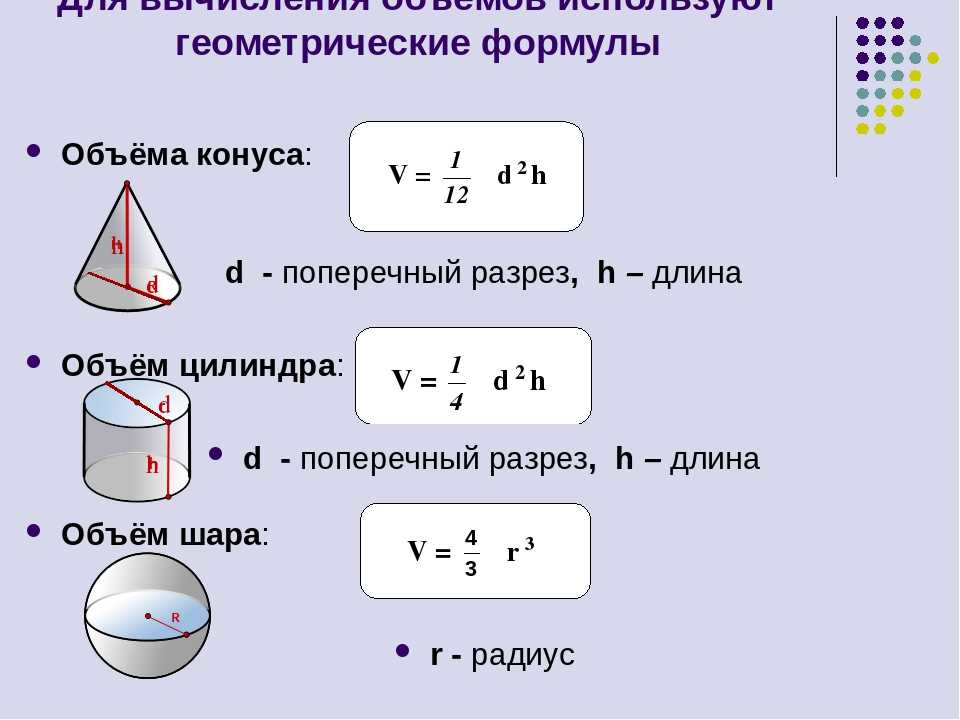 Обратите внимание на следующий рисунок, чтобы увидеть равные стороны куба и пространство, которое он занимает.
Обратите внимание на следующий рисунок, чтобы увидеть равные стороны куба и пространство, которое он занимает.
Объем цилиндра
Точно так же, как мы построили прямоугольный параллелепипед из прямоугольников, мы можем построить цилиндр из кругов того же размера.
Цилиндр представляет собой трубчатую конструкцию с двумя параллельными круглыми основаниями, которые соединены изогнутой поверхностью на фиксированном расстоянии от центра. Расстояние между этими двумя основаниями и есть высота цилиндра. Если мы рассмотрим «r» как радиус круглого основания (и вершины), а «h» как высоту цилиндра, то объем цилиндра можно выразить как объем цилиндра = π r² h
Объем пирамиды
Пирамиды имеют многоугольник в качестве основания и треугольные грани, которые сходятся на вершине. Объем пирамиды рассчитывается по формуле: Объем пирамиды = 1/3 × длина основания × ширина основания × высота пирамиды. Эту формулу также можно записать в виде 1/3 × площадь основания многоугольника × высота пирамиды.
Объем конуса
Разница между конусом и пирамидой в том, что основание конуса круглое, а основание пирамиды многоугольник. Объем конуса рассчитывается по формуле: 1/3 × πr 2 ч.
Объем шара
Объем шара – это занимаемое им пространство.
Объем сферы, радиус которой r равен 4/3 πr³.
Теперь, когда мы знакомы с формулами различных геометрических фигур, давайте взглянем на различные единицы объема.
Список формул объема
Ниже приведен подробный табличный список формул объема в двух словах, описывающий формулы объема для всех возможных трехмерных (теловидных) форм.
Как рассчитать объем?
Вот шаги для расчета объема любой твердой формы:
- Определите все заданные параметры, которые являются полезными и которые необходимо заменить в соответствующей формуле объема. Например, радиус должен быть «r», а высота — «h», наклонная высота, диаметр и т.
 д.
д. - Убедитесь, что все параметры имеют одинаковые единицы измерения.
- Подставьте значения в формулу объема соответствующих фигур.
- Запишите единицы измерения в кубических единицах.
Давайте разберемся с шагами на примере.
Пример: Найдите объем прямоугольного цилиндра радиусом 25 м и высотой 1 метр. Используйте π = 3,142.
Решение:
Радиус цилиндра r = 25 м.
Его высота h = 1 метр.
Объем цилиндра V = πr 2 h = (3,142)(25) 2 (1) = 1963,75 м 3 .
Объем баллона 1963,75 куб.м.
Единицы объема
Единицей объема в системе СИ является кубический метр (м 3 ), поскольку объем представляет собой количество трехмерного пространства, занимаемого формой или поверхностью. Однако наиболее часто используемой единицей измерения объема является литр. Кроме того, большие и малые объемы измеряются в других единицах, таких как миллилитры (мл), пинты, галлоны и другие. В следующей таблице показаны несколько единиц, связанных с объемом, и их метрические эквиваленты.
В следующей таблице показаны несколько единиц, связанных с объемом, и их метрические эквиваленты.
| Боковой блок | Единица объема | Метрический эквивалент |
|---|---|---|
| Дюйм | Кубические дюймы (в 3 ) | 1 куб. дюйм = 16,387064 мл |
| Ножка | Кубические футы (футы 3 ) | 1 куб.фут = 28,316846592 л |
| см | Кубический сантиметр (см 3 ) | 1 кубический сантиметр = 1 мл |
| Двор | Кубический ярд (ярд 3 ) | 1 куб.ярд = 764,554857984 л 1 куб.ярд = 0,764554857984 м 3 |
В то время как стандартной единицей измерения в США является кубический ярд или кубический дюйм, более широко используемыми единицами измерения являются галлоны, пинты или жидкие унции. В следующей таблице показаны некоторые из этих единиц и их эквивалентные метрические преобразования.
| Блок | Эквивалентное преобразование |
|---|---|
| 1 пинта (pt) | 2 чашки |
| 1 кварта (кварт) | 2 балла |
| 1 галлон (гал) | 3,78 литра |
| 1 литр | 1000 кубических сантиметров |
Калькулятор объема
Калькулятор объема помогает быстро и легко рассчитать объем любой заданной формы. Объем — это раздел математики, который занимается измерением емкости различных твердых тел. Попробуйте калькулятор объемов Cuemath прямо сейчас. Это онлайн-инструмент для простых и быстрых расчетов.
☛Также проверьте:
- Калькулятор объема цилиндра
- Калькулятор объема сферы
- Калькулятор объема куба
- Калькулятор объема прямоугольного параллелепипеда
☛Статьи по теме
Ознакомьтесь со статьями, посвященными объему различных объемных форм.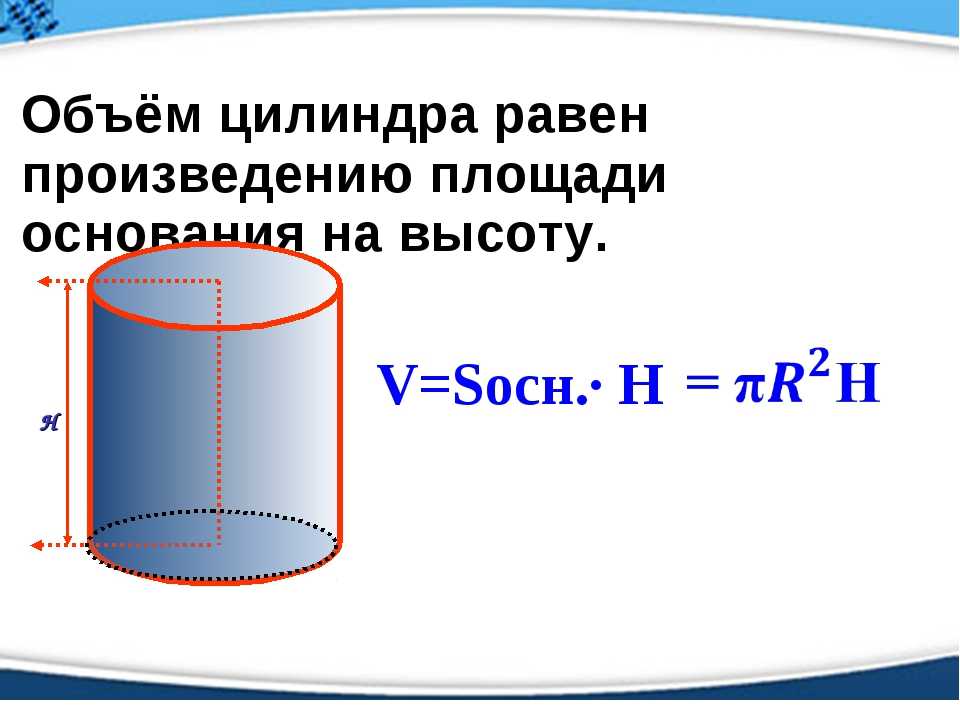
- Объем конуса
- Объем цилиндра
- Объем прямоугольного параллелепипеда
- Том Пирамиды
Примеры томов
Пример 1: У Эдвина есть конический сосуд радиусом 6 дюймов и высотой 7 дюймов. Каков объем сосуда? Используйте π = 22/7.
Раствор.
Сосуд имеет форму конуса.
Объем конуса = 1/3 π r² h = 1/3 × 22/7 × 6 × 6 × 7 = 264 дюйма³
∴ Объем судна 264 куб. дюймПример 2: Джо любит играть со строительными блоками. Он построил конструкцию из 15 кубов. Если длина (ребро) каждого куба равна 3 дюймам, каков будет объем его конструкции?
Раствор.
Рассчитаем объем одного куба. Объем куба = ребро × ребро × ребро = 3 × 3 × 3 = 27 дюймов³
В его структуре 15 кубиков. Итак, объем всей конструкции:
Объем конструкции = 15 × объем одного куба = 15 × 27 = 405 дюймов³
∴ Объем конструкции 405 дюймов³.
Пример 3: Если диаметр мяча 14 дюймов, сколько воздуха может вместить мяч? Используйте π = 3,14
Решение.
Количество воздуха внутри шара займет все пространство в шаре. Итак, нам нужно найти объем шара.
Радиус шара 14/2 дюйма = 7 дюймов
Объем шара = 4/3 πr³
= [4/3 × 3,14 × (7)³]
= 1436,02 дюйма³
∴ Мяч содержит 1436,02 дюйма³ воздуха.
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, что стоит за математикой, с нашими сертифицированными экспертами
Запишитесь на бесплатный пробный урок
Практические вопросы по объему
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о томе
Что означает объем?
Объем — это мера емкости, которую содержит объект. Скажем, если чашка может вместить 1000 мл сока, говорят, что ее объем равен 1000 мл. В этом случае объем также можно определить как количество сока, занимаемое чашкой. Объем всегда рассчитывается путем деления емкости фигур на равные кубические единицы.
Скажем, если чашка может вместить 1000 мл сока, говорят, что ее объем равен 1000 мл. В этом случае объем также можно определить как количество сока, занимаемое чашкой. Объем всегда рассчитывается путем деления емкости фигур на равные кубические единицы.
☛Загрузите прямо сейчас, чтобы попрактиковаться.
- Объемные листы
- Объем кубов Рабочие листы
- Рабочий лист «Объем конуса»
- Объем цилиндра Рабочие листы
Какова формула объема частичного конуса?
Объем частичного конуса можно рассчитать по формуле: V = 1/3 × πh(R² + Rr + r²), где «R» — радиус основания конуса, а «r» — радиус верхней поверхности.
☛ Прочтите основы здесь:
- Объем правого кругового конуса
- Объем частичного конуса
- Объем конуса в единицах числа Пи
Как найти объем пирамид?
Объем пирамиды рассчитывается по формуле: V = 1/3 × Площадь основания × Высота.
☛ Также проверьте:
- Объем прямоугольной пирамиды
- Объем треугольной пирамиды
- Объем прямоугольной пирамиды
Как найти объем конуса?
Объем конуса составляет 1/3 объема цилиндра той же высоты и того же основания. Формула, используемая для нахождения объема конуса: 1/3 × π r² h; где «r» — радиус, а «h» — высота конуса.
Как найти объем цилиндра?
Объем цилиндра рассчитывается по формуле: V = площадь основания цилиндра × высота, а также представляется как объем цилиндра = π r² h; где «r» — радиус цилиндра, а «h» — высота.
В чем разница между объемом и площадью?
Объем фигуры или твердого тела — это пространство, занимаемое им, которое также включает его высоту или глубину. Измеряется в кубических единицах. Площадь – это пространство, занимаемое поверхностью плоской формы. Измеряется в квадратных единицах.
☛ Проверьте список важных математических формул:
- Формулы площади
- Формулы площади поверхности
- Геометрические формулы
- Формулы измерения
Каков объем мяча?
Поскольку шар является сферой, его объем будет рассчитан по формуле объема сферы. Формула объема сферы: 4/3 πr³, где «r» — радиус сферы.
Формула объема сферы: 4/3 πr³, где «r» — радиус сферы.
Какая формула объема цилиндра?
Формула объема цилиндра = πr²h; где «r» — радиус основания цилиндра, а «h» — высота.
Как найти объем призмы?
Мы можем найти объем призмы, записав заданные размеры призмы. Затем подставьте значения в формулу объема V = B × H, где «V», «B» и «H» — это объем, площадь основания и высота призмы. Получив значение объема призмы, в конце запишите единицу объема призмы (в кубических единицах).
☛Чек:
- Объем призмы
- Объем призм с заданиями
Как найти объем бака?
Объем резервуара зависит от его формы. В зависимости от размера мы можем использовать приведенные ниже формулы:
- Объем параллелепипеда = l × b × h; где «l» — длина прямоугольного параллелепипеда, «b» — ширина (ширина) прямоугольного параллелепипеда, а «h» — высота прямоугольного параллелепипеда.
- Объем куба = a 3 , где «a» — ребро куба.

 Например, у двух одинаковых пакетов сока равные объемы.
Например, у двух одинаковых пакетов сока равные объемы.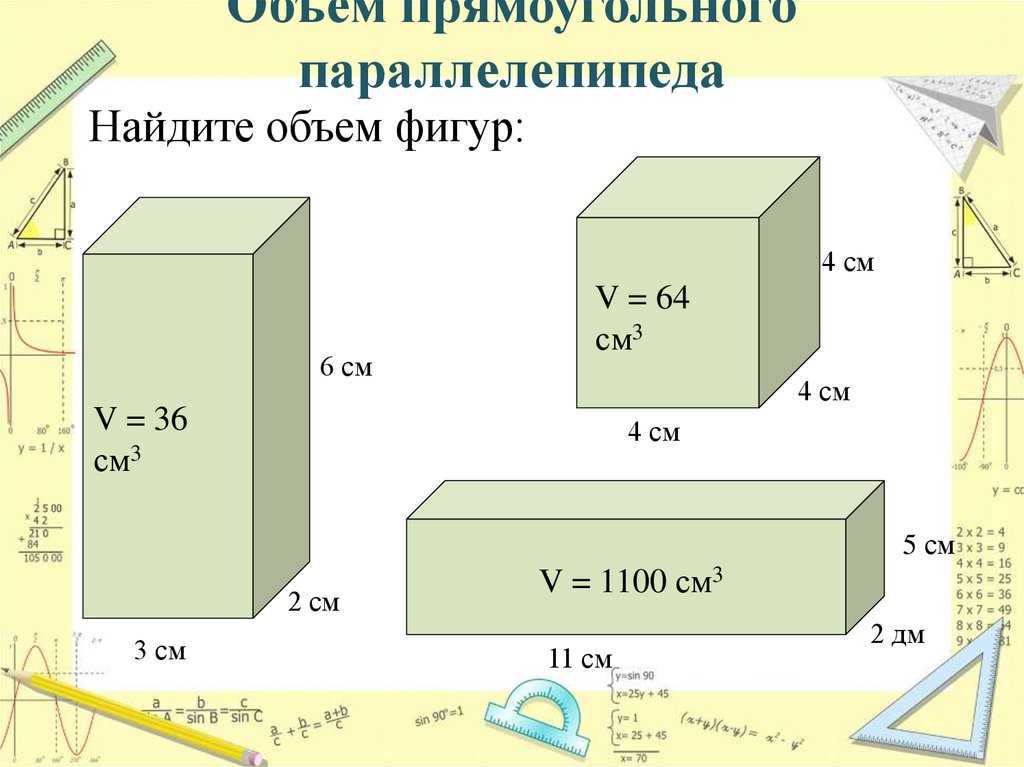 п. = 2 (ab + ac + bc)
п. = 2 (ab + ac + bc) д.
д.