Развертка конуса или как построить развертку конуса. Конус развертка

Развертка конуса | Начертательная геометрия

Развертка конуса строится таким же способом, который используются при развертывании боковой поверхности пирамиды - способом треугольников. Коническая поверхность заменяется многогранной пирамидальной поверхностью, вписанной в данную коническую.

Развертка конуса

Развертка конуса вращения

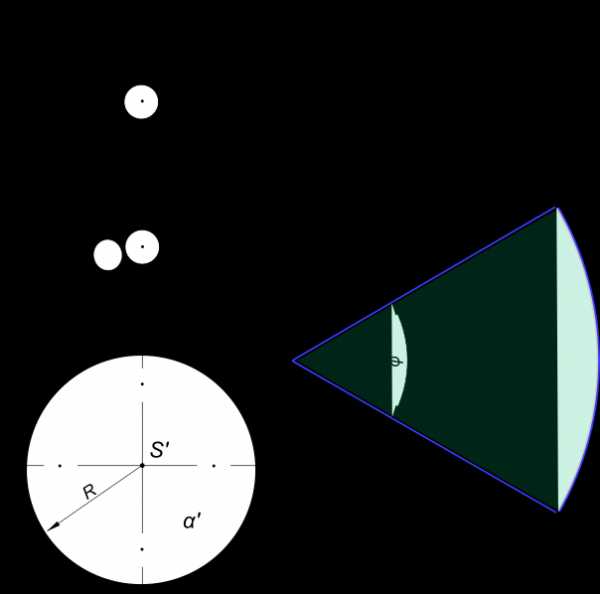
Развертка конуса

представляет круговой сектор, радиус которого равен длине образующей конической поверхности L = |SA|, а центральный угол: φ = 360° *(R/L).

Развертка конуса вращения усеченного

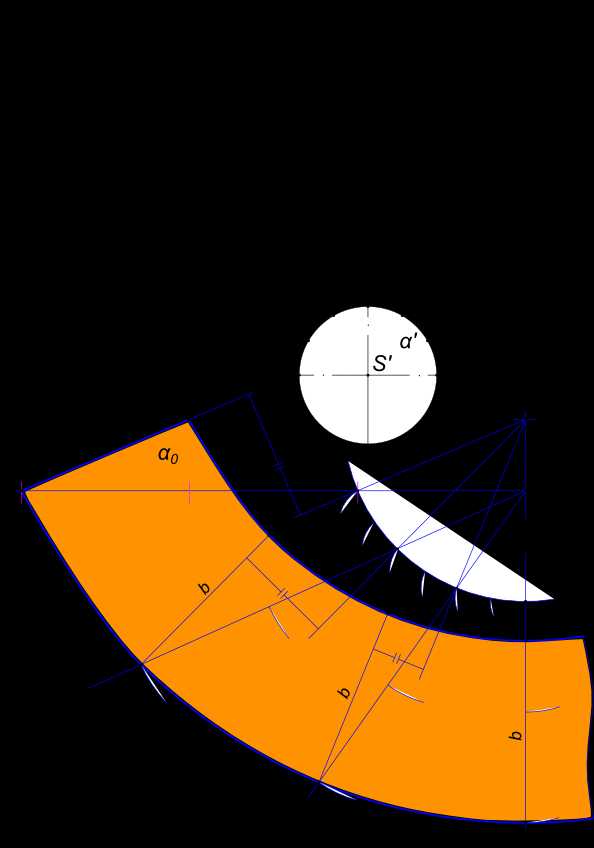
Развертка конуса

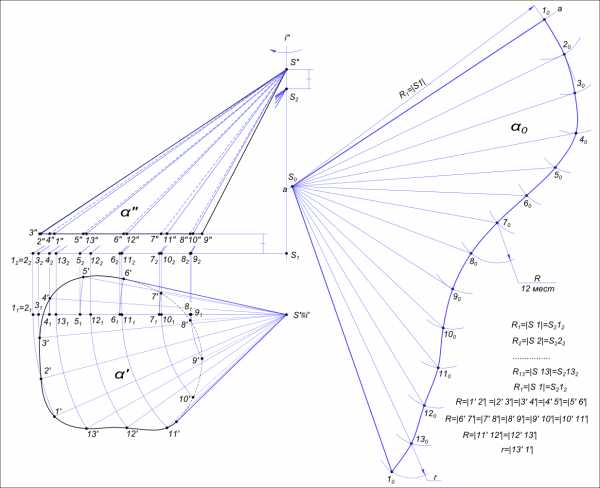
На рисунке представлено построение развертки боковой поверхности усеченного конуса без построения его вершины: - на чертеже усеченного конуса строится вспомогательный конус подобный заданному из условия K=D/d1, K - коэффициент кратности оснований конусов целое число. Принимаем K=3; - разделим половину окружности основания d1 на 6 равных частей; - строим развертку вспомогательного конуса с вершиной S по точкам на дуге развертки; - на оси симметрии развертки (биссектриса полной развертки) выбрать произвольную точку K и провести семейство лучей , соединяющих ее с точками 0, 2, 4, 6 развертки вспомогательного конуса; - откладываем на проведенных лучах отрезки, величины которых равны: KO0 = K*K0; K20 = K*K2; K40 = K*K4; K60 = K*K6; - через построенные точки 00, 20, 40, 60 проводим прямые параллельные соответствующим образующим развертки вспомогательного конуса, откладывая на них натуральную величину b образующей усеченного конуса и отмечая при этом точки O0, 20, 40, 60; - соединяем построенные точки плавными линиями и получаем искомую развертку.

Развертка конуса вращения усеченного плоскостью общего положения выполнено в Графическая работа 13.

ngeo.fxyz.ru

Развертка конуса. Урок.

Anton Dmz 04.05.2011

Развертка конуса

Выполним одно из простых, но часто используемых в черчении построений – построим развертку боковой поверхности конуса. В Autocad есть средства, позволяющие быстро и точно решать подобные задачи.

1. Для начала вспомним школьный курс геометрии:

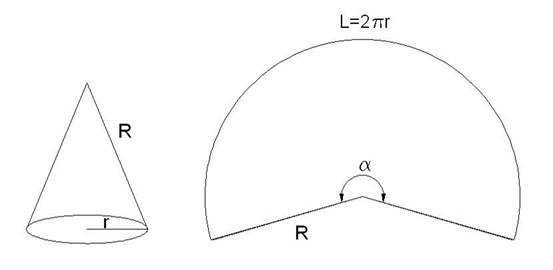
Развертка боковой поверхности прямого конуса – это сектор круга, радиус которого равен образующей конуса R, а длина дуги L=2?r, где r – радиус основания конуса. Угол ? в градусах равен 360 * 2? r/2?R = 360r/R.

2. Пусть конус задан графически в виде треугольника (для твердотельного конуса построение также справедливо):

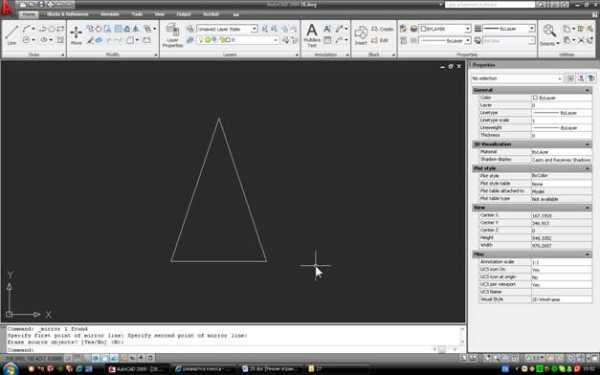
Построим его развертку. Вариантов такого построения очень много, мы же применим способ, который не требует сторонних расчетов и использует только инструменты Autocad. Сначала построим произвольную дугу с радиусом R. Для этого начертим окружность, используя образующую конуса в качестве радиуса:

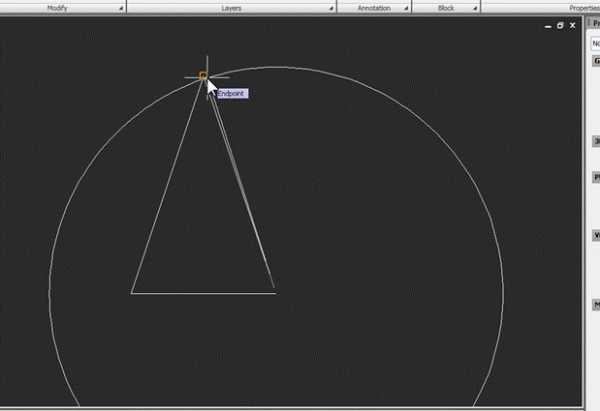
Затем командой Trim отсечем от нее любую часть, чтобы она превратилась в дугу. В качестве режущей кромки используем произвольную вспомогательную линию:

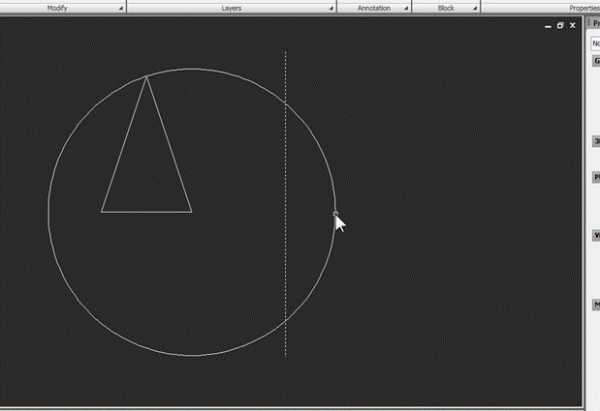
Затем линию удаляем, выделяем дугу и открываем окно свойств:

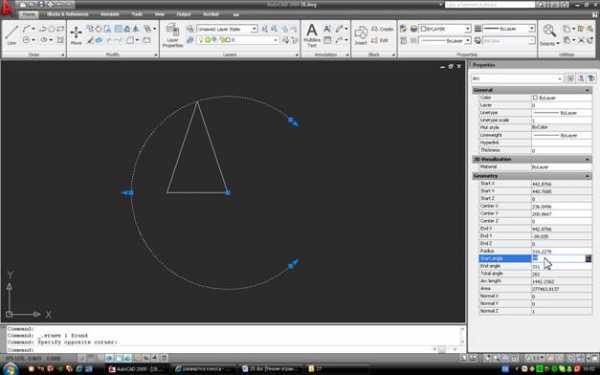
Изменяем Start angle – устанавливаем его в 0. Затем в окошке End angle нажимаем значок встроенного калькулятора:

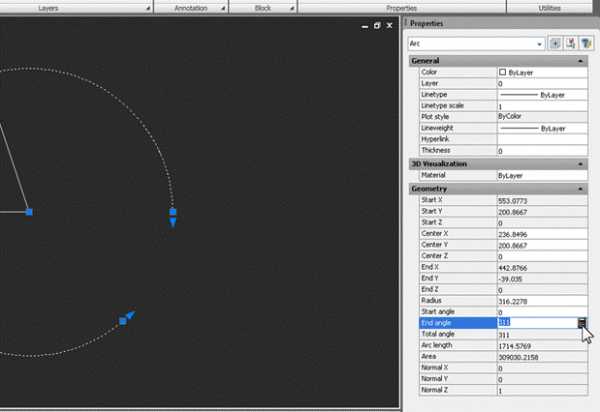
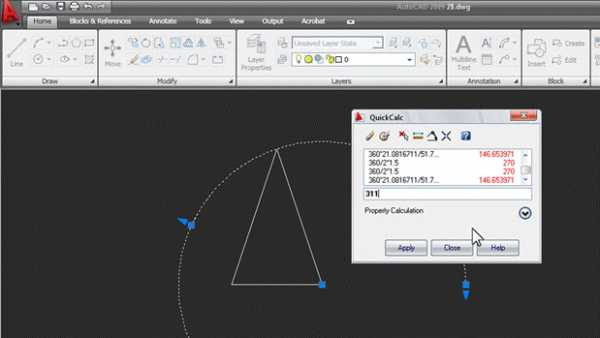
В появившемся окне «вычисляем» угол. Набираем с клавиатуры 360* и жмем кнопку с линейкой:

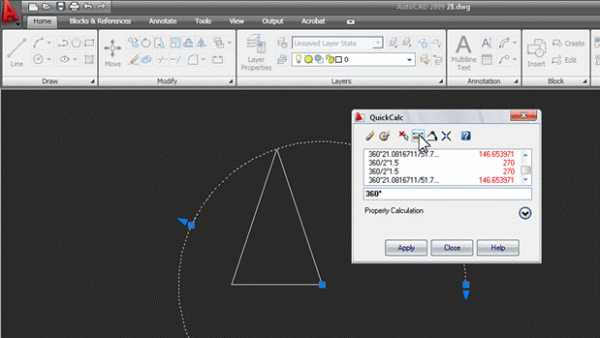
Указываем на экране радиус основания конуса двумя точками (середина основания и нижняя вершина треугольника). Затем c клавиатуры вводим знак деления / и таким же образом указываем длину образующей конуса. В итоге в окне появляется выражение с параметрами вашего конуса:

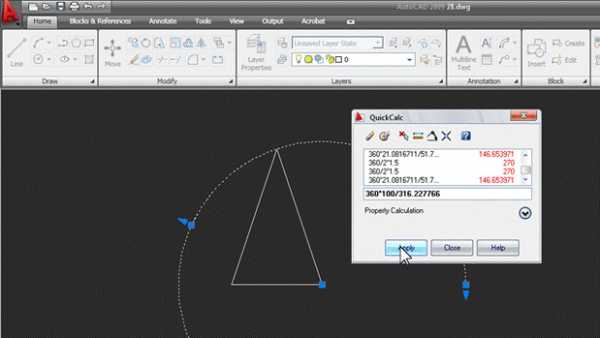
Жмем Apply, и угол автоматически вычисляется и присваивается свойству End angle:

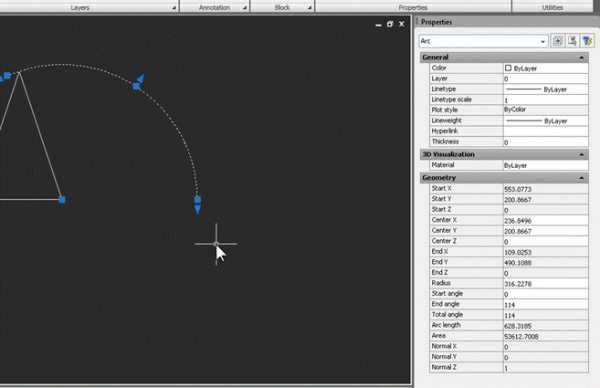
3. Построим основание конуса, чтобы развертка стала полной, и проверим правильность построений. Строим окружность на основании треугольника, как на диаметре, и переносим ее так, чтобы она касалась наружной дуги развертки:

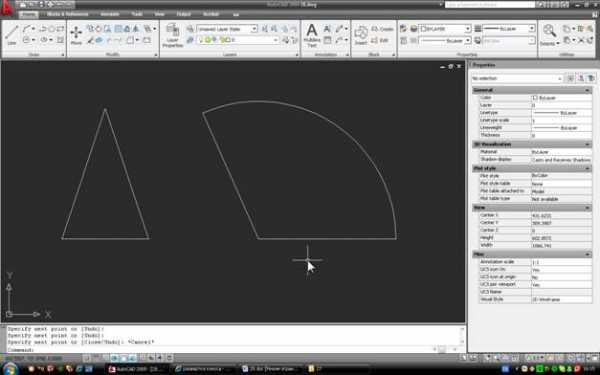
Вот готовая развертка:

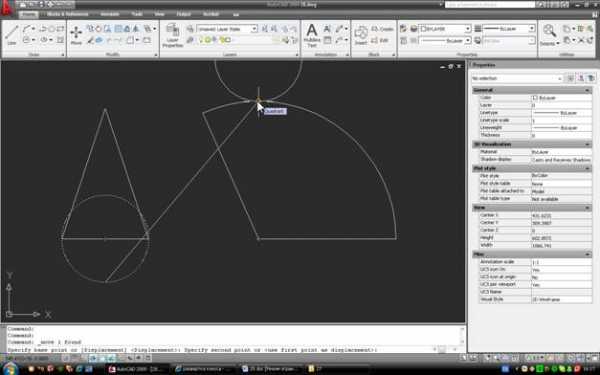
Теперь, если по очереди выделить окружность-основание и дугу, можно в свойствах сравнить их длины. У окружности это свойство называется Circumference, у дуги – Arc length:

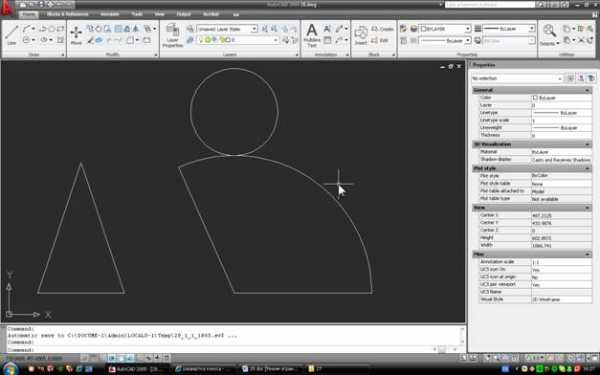
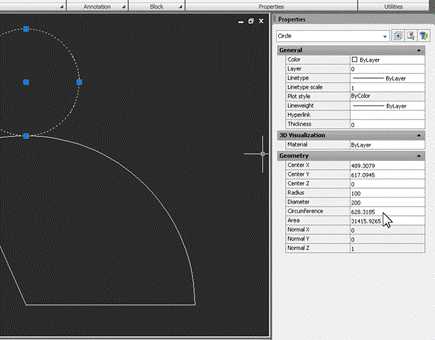
Если построения выполнены правильно, числа должны совпасть.

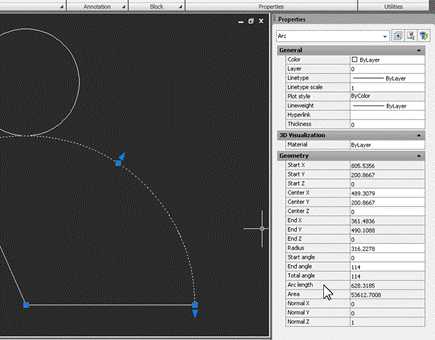
Как видим, строить развертку конуса (как и многих других геометрических тел) в Autocad гораздо проще, чем на бумаге.

Источник: http://autocad-lessons.ruСтудия Vertex. Только качественные уроки AutoCAD.

procae.ru

Построение разверток тел вращения - это... Что такое Построение разверток тел вращения?

Построение разверток тел вращения

Окружающий нас мир динамичен и разнообразен, и далеко не всякий объект можно просто обмерить линейкой. Для подобного переноса используются специальные техники, как то триангуляция.Потребность в составлении сложных развёрток, как правило, возникает при моделировании, работе с бумагой и металлом, в слесарном деле. Написанная ниже статья, объясняет принципы построения развёрток тел вращения (цилиндр, конус) и их частных случаев (сечение конуса, конус с переходом с круга на квадрат).

Основы и инструмент

Все нижеописанные действия выполняются на бумаге, при помощи линейки, карандаша и циркуля. Рекомендуется комплект лекал, для повышения точности и качества развёрток.
При изготовлении развёрток на металле используется метровая линейка, чертилка, циркуль по металлу, комплект лекал, молоток и керно, для отметки узловых точек.

Длина окружности считается по формуле:

илиГде: — радиус окружности, — диаметр окружности, — длина окружности, — Число Пи (Pi),Как правило, для вычисления используется значение (Pi) до второго знака (3,14), но в некоторых случаях, этого может быть недостаточно.

Усечённый конус с доступной вершиной: Конус, при построении которого можно определить положение вершины.
Усечённый конус с недоступной вершиной: Конус, при построении которого положение вершины определить затруднительно, в виду её удалённости.
Триангуляция: способ построения разверток поверхностей неразвертывающихся, конических, общего вида и с ребром возврата.
Следует помнить: Независимо от того, является рассматриваемая поверхность развертываемой или неразвертываемой, графически может быть построена только приближенная развертка. Это объясняется тем, что в процессе снятия и откладывания размеров и выполнения других графических операций неизбежны погрешности, обусловливаемые конструктивными особенностями чертежных инструментов, физическими возможностями глаза и погрешностями от замены дуг хордами и углов на поверхности плоскими углами. Приближенные развертки кривых не-развертывающихся поверхностей, кроме графических погрешностей, содержат погрешности, полученные за счет несовпадения элементов таких поверхностей с плоскими аппроксимирующими элементами. Поэтому для получения поверхности из такой развертки, кроме изгибания, необходимо произвести частичное растяжение и сжатие отдельных ее участков. Приближенные развертки при тщательном выполнении обладают точностью, достаточной для практических целей.

Представленный в статье материал, подразумевает, что вы имеете представление об основах черчения, умеете делить окружность, находить центр отрезка при помощи циркуля, снимать/переносить размеры циркулем, пользоваться лекалами, и соответствующим справочным материалом. Потому, объяснение многих моментов в статье опущено.

Построение развёртки цилиндра

Цилиндр

Тело вращения с наиболее простой развёрткой, имеющей форму прямоугольника, где две параллельные стороны соответствуют высоте цилиндра, а две другие параллельные стороны — длине окружности оснований цилиндра.

Усечённый цилиндр (рыбина)

Усечённый цилиндр

Подготовка:

Для создания развёртки, начертим четырёхугольник ACDE в натуральную величину (см.чертёж).

Проведём перпендикуляр BD, из плоскости AC в точку D, отсекая от построения прямую часть цилиндра ABDE, которую можно достроить по мере надобности.
Из центра плоскости CD (точка O) проведём дугу, радиусом в половину плоскости CD, и разделим её на 6 частей. Из получившихся точек O, проведём перпендикулярные прямые к плоскости CD. Из точек на плоскости CD, проведём прямые, перпендикулярные к плоскости BD.

Построение:

Отрезок BC переносим, и превращаем в вертикаль. Из точки B, вертикали BC, проводим луч, перпендикулярный вертикали BC.
Циркулем снимаем размер C-O1, и откладываем на луче, из точки B, точку 1. Снимаем размер B1-C1, и откладываем перпендикуляр из точки 1.
Циркулем снимаем размер O1-O2, и откладываем на луче, из точки 1, точку 2. Снимаем размер B2-C2, и откладываем перпендикуляр из точки 2.
Повторять, пока не будет отложена точка D.
Получившиеся вертикали, из точки C, вертикали BC, до точки D — соединить лекальной кривой.
Вторая половина развёртки зеркальна.

Подобным образом строятся любые цилиндрические срезы.Примечание: Почему "Рыбина" — если продолжить построение развёртки, при этом половину построить от точки D, а вторую в обратную сторону от вертикали BC, то получившийся рисунок, будет похож на рыбку, или рыбий хвост.

Чертёж: "Усечённый цилиндр"

Построение развёртки конуса

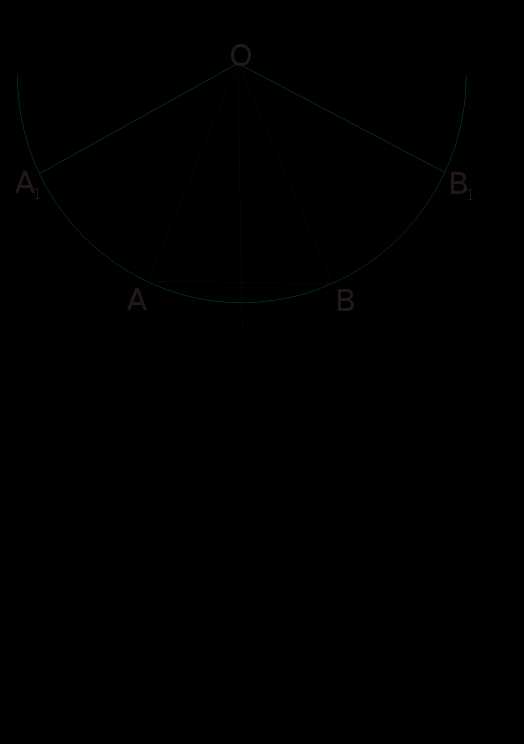
Конус

Развёртка конуса может быть выполнена двумя способами. (См. чертёж)

Если известен размер стороны конуса, из точки O, циркулем чертится дуга, радиусом равным стороне конуса. На дуге откладываются две точки (A1 и B1), на расстоянии равном длине окружности и соединяются с точкой О.
Строится конус в натуральную величину, из точки O, в точку A, ставится циркуль, и проводится дуга, проходящая через точки A и B. На дуге откладываются две точки (A1 и B1), на расстоянии равном длине окружности и соединяются с точкой О.

Для удобства, от можно откладывать половину длинны окружности, в обе стороны от осевой линии конуса.Конус со смещёной вершиной строиться так же, как усечённый конус со смещёнными основаниями.

Как отложить длину окружности на дуге:

При помощи нитки, длина которой равна длине окружности.

При помощи металической линейки, которую следует изогнуть «по дуге», и поставить соответствующие риски.
Построить окружность основания конуса в виде сверху, в натуральную величину. Разделить окружность на 12 или более равных частей, и отложить их на прямой поочерёдно.

Чертёж: "Конус"

Конус с прямоугольным (многогранным) основанием.

Конуса с многогранным основанием

В случае, если конус имеет ровное, радиальное, основание: (При построении окружности на виде с верху, путём установки циркуля в центр, и очерчивания окружности по произвольной вершине — все вершины основания укладываются на дугу окружности.) Построить конус, по аналогии с развёрткой обычного конуса (основание строить по окружности, от вида сверху). Отложить дугу из точки O. В произвольной части дуги поставить точку A1, и поочерёдно отложить все грани основания на дугу. Конечная точка последней грани будет B1.
Во всех иных случаях конус строится по принципу триангуляции (см. далее).

Усечённый конус с доступной вершиной

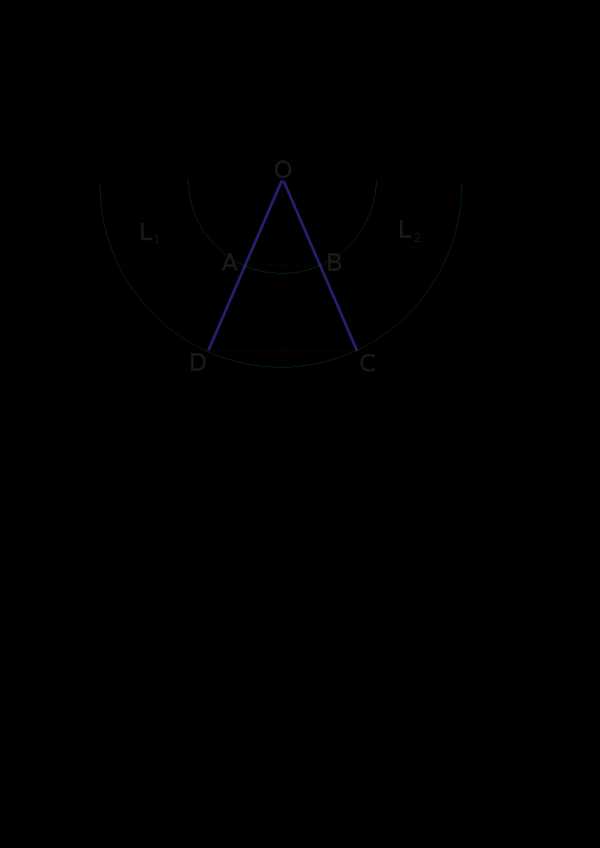
Усечённый конус

Построить усечённый конус ABCD в натуральную величину (См. чертёж).Стороны AD и BC продожить, до появления точки пересечения O. Из точки пересечения O, провести дуги, с радиусом OB и OC.На дуге OC, отложить длину окружности DC. На дуге OB, отложить длину окружности AB. Полученные точки соединить отрезками L1 и L2.Для удобства, от можно откладывать половину длинны окружности, в обе стороны от осевой линии конуса.

Как отложить длину окружности на дуге:

При помощи нитки, длина которой равна длине окружности.
При помощи металической линейки, которую следует изогнуть «по дуге», и поставить соответствующие риски.

Примечание: Совсем не обязательно, что отрезки L1 и L2, если их продолжить, будут сходится в точке O. Если быть до конца честным, то сойтись они должны, но с учётом поправок на погрешности инструмента, материала и глазомера — точка пересечения может оказаться чуть ниже или выше вершины, что не является ошибкой.

Чертёж: "Усечённый конус"

Усечённый конус с переходом с круга на квадрат

Конус с переходом с круга на квадрат

Подготовка:Построить усечённый конус ABCD в натуральную величину (см. чертёж), построить вид сверху ABB1A1. Окружность поделить на равные части (в приведённом примере показано деление одной четверти). Точки AA1-AA4 соединить отрезками с точкой A. Провести ось O, из центра которой провести перпендикуляр O-O1, высотой равной высоте конуса.Ниже, первичные размеры снимаются с вида сверху.Построение:

Снять размер AD и построить произвольную вертикаль AA0-AA1. Снять размер AA0-A, и поставить «примерную точку», сделав отмашку циркулем. Снять размер A-AA1, и на оси O, из точки O, отложить отрезок, снять размер из полученной точки до точки O1. Сделать отмашку циркулем из точки AA1, до предполагаемой точки A. Соединить отрезками точки AA0-A-AA1.
Снять размер AA1-AA2, из точки AA1 поставить «примерную точку», сделав отмашку циркулем. Снять размер A-AA2, и на оси O, из точки O, отложить отрезок, снять размер из полученной точки до точки O1. Сделать отмашку циркулем из точки A, до предполагаемой точки AA2. Провести отрезок A-AA2. Повторить, пока не будет отложен отрезок A-AA4.
Снять размер A-AA5, из точки A поставить «примерную точку» AA5. Снять размер AA4-AA5, и на оси O, из точки O, отложить отрезок, снять размер из полученной точки до точки O1. Сделать отмашку циркулем из точки AA4, до предполагаемой точки AA5. Провести отрезок AA4-AA5.

Подобным образом построить остальные сегменты.Примечание: Если конус имеет доступную вершину, и КВАДРАТНОЕ основание - то построение можно провести по принципу усечённого конуса с доступной вершиной, а основание — конуса с прямоугольным (многогранным) основанием. Точность будет ниже, но построение существенно проще.

Чертёж: "Конус с переходом с круга на квадрат"

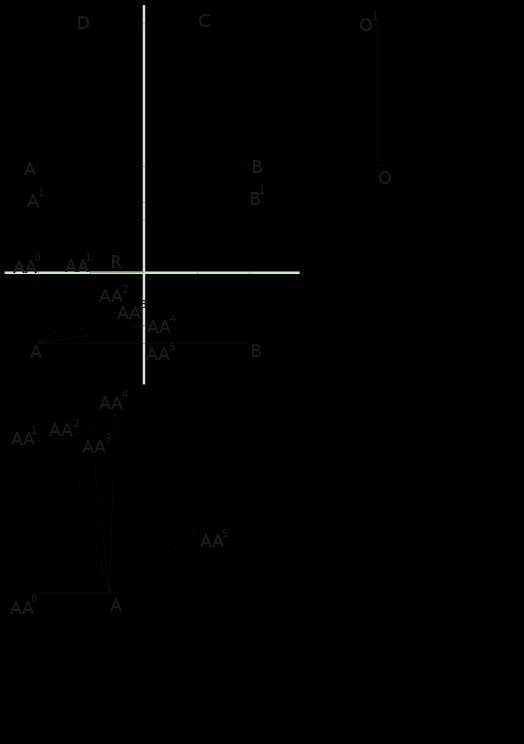
Усечённый конус с непараллельными основаниями

Усечённый конус с не параллельными основаниями

Готовлю чертежи

Усечённый конус со смещёнными основаниями

Усечённый конус со смещёнными основаниями Усечённый конус со смещёнными основаниями в векторном представлении

Готовлю чертежи

Обобщения и замечания

Используя вышеприведённую технику, можно построить развёртку практически любого объекта со сложной топографией.
При этом следует иметь в виду, что при работе с металлом следует брать внутренние размеры детали, т.к. при гибке и/или закатке, внешняя поверхность металла тянется, а внутренняя остаётся неизменной. (Верно при использовании современного гибочного оборудования. На устаревшем оборудовании, следует вводить поправки на износ поверхностей, и точность работы станка.)
При работе с металлом, толщиной свыше 6 мм, в зависимости от типа, марки металла и используемого гибочного оборудования - размеры следует брать не по внутренней стороне, а по «средней линии», которая проходит на половине толщины металла.
При изготовлении из металла, линии разметки (прямые, а не вспомогательные диагонали) могут использоваться как линии гиба, с последующей доводкой контура молотком/киянкой на вспомогательной поверхности.

Смотри так же

ГОСТ 2.301-68* Форматы. (размеры форматов и их обозначение)
Начертательная геометрия и черчение.Книга начертательная геометрия и машиностроительное черчение. Под редакцией Чекмарева А.А.
Справочное руководство по черчению. Под редакцией Е.И. Годик и А.М. Хаскин. Москва "МАШИНОСТРОЕНИЕ" 1974г.
ЧЕРЧЕНИЕ. Под редакцией Боголюбова С.К. Учебник для средних специальных учебных заведений (2-е изд.)

dic.academic.ru

Развертка конуса в AutoCAD - как сделать правильно

Выполним одно из простых, но часто используемых в черчении построений – построим развертку конуса (боковой поверхности). В Autocad есть средства, позволяющие быстро и точно решать подобные задачи.

1. Для начала вспомним школьный курс геометрии:

Затем линию удаляем, выделяем дугу и открываем окно свойств:

Изменяем Start angle – устанавливаем его в 0. Затем в окошке End angle нажимаем значок встроенного калькулятора:

В появившемся окне «вычисляем» угол. Набираем с клавиатуры 360* и жмем кнопку с линейкой:

Жмем Apply, и угол автоматически вычисляется и присваивается свойству End angle:

Вот готовая развертка:

Если построения выполнены правильно, числа должны совпасть.

autocad-lessons.ru

Развертка конуса или как построить развертку конуса

Дано: Пересечение конуса и цилиндра. Необходимо: Построить развертку конуса и нанести на ней линию их пересечения.

В этом видеоуроке построим развертку конуса. Построение развертки конуса не сложнее чем ранее рассмотренные развертки многогранников: Развертка пирамиды и Развертка призмы.

Как построить развертку конуса и нанести на ней линию их пересечения?

Построить развертку конуса можно 2 путями:

Разделить основание конуса на 12 частей (вписываем правильный многогранник – пирамиду). Можете разделить основание конуса и на большее или меньше количество частей, т.к. чем меньше хорда, тем точнее построение развертки конуса. Затем на дугу кругового сектора перенести хорды.
Построение развертки конуса, по формуле определяющей угол кругового сектора.

Так как нам необходимо нанести на развертку конуса линии пересечения конуса и цилиндра, то нам все равно придется делить основание конуса на 12 частей и вписывать пирамиду, поэтому мы пойдем сразу по 1 пути построения развертки конуса.

Алгоритм построения развертки конуса

Делим основание конуса на 12 равных частей (вписываем правильную пирамиду).
Строим боковую поверхность конуса, которая представляет собой круговой сектор. Радиус кругового сектора конуса равен длине образующей конуса, а длина дуги сектора равна длине окружности основания конуса. На дугу сектора переносим 12 хорд, которые определят ее длину, а также угол кругового сектора.
К любой точке дуги сектора пристраиваем основание конуса.
Через характерные точки пересечения конуса и цилиндра проводим образующие.
Находим натуральную величину образующих.
Строим данные образующие на развертке конуса.
Соединяем характерные точки пересечения конуса и цилиндра на развертке.

Более подробно в видеоуроке по начертательной геометрии в Автокад.

Во время построения развертки конуса мы будем использовать Массив в Автокад - Круговой массив и массив по траектории. Рекомендую к просмотру данные видеоуроки Автокад. Видеокурс Автокад 2D на момент написания статьи содержит классический способ построения кругового массива и интерактивный при построении массива по траектории.

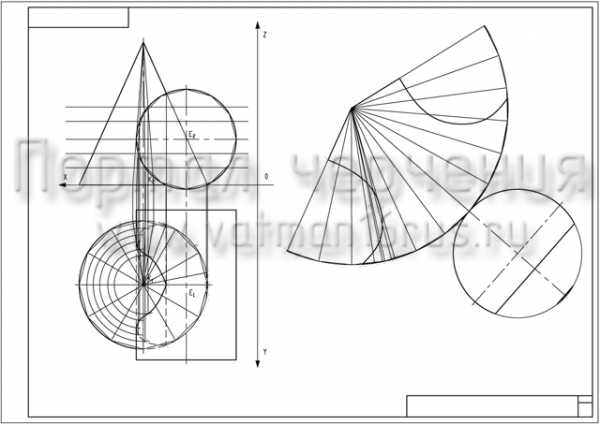
Видео "Развертка конуса или как построить развертку конуса"

P.S.

Этот видеоурок и статья входят в профессиональный бесплатный самоучитель Автокад, который подходит как для начинающих пользователей, так и уже давно работающих в Автокад.

Тематика писем:

Выберите из спискаВсе статьиAutoCAD 2DAutoCAD 3DAutoCAD Architecture КомпасInventor3D maxRevitОсновы черченияНачертательная геометрияИнженерная графикаМашиностроительное черчениеСтроительное черчениеСхемы

drawing-portal.com

Развертка коническая – какие задачи решает такое приспособление? + видео

Развертка коническая (ГОСТ 10083-81) – один из видов большого класса инструментов, которые призваны корректировать грубо проделанное отверстие в какой-либо поверхности. О ее работе мы и поговорим ниже.

Развертка ручная коническая и другие разновидности приспособления

Для того чтобы получить отверстия с чистой поверхностью или же в случае, если требуется точная подгонка отверстия под какую-то шлифованную деталь, производится процесс, называемый развертыванием. Его можно выполнить вручную или же использовать для этого сверлильный станок, на который устанавливаются развертки. В первом случае при производстве работ ручная коническая развертка вращается воротком.

Эти инструменты бывают цилиндрическими, коническими и ступенчатыми (по типу отверстия, обрабатываемого ими). В отношении точности они делятся на следующие: указывающие квалитет (для цилиндрических разверток), те, что указывают качество (черновые, чистовые и промежуточные между ними – для конических типов). Сюда же можно отнести развертки цилиндрические с калиброванным припуском, необходимые для того, чтобы дальше шлифовать инструмент до нужного размера. И последний тип в этой группе – регулируемые развертки.

По тому, каким способом зажимаются, они делятся на:

ручные (у них имеется квадратный хвостик под вороток),
машинные (с цилиндрическим или коническим хвостовиком),
насадные для машин (устанавливаются на специальную оправку, как правило, нужны для инструментов, имеющих большие размеры).

На рабочей части этого приспособления есть нарезанные зубья, как правило, их от 6 до 14, вдоль них расположены канавки, образующие режущие кромки.

Часть, которая находится снизу развертки, предназначена для снимания стружки, а та, что вверху, названная калибрующей, может пускать инструмент в нужном направлении, чтобы полностью калибровать отверстия. В целом инструмент необходим для того, чтобы развертывать конусные отверстия. Припуск, допускаемый при черновом этапе работ, составляет не более пятой части одного миллиметра, а для чистового принимается равным десятой части миллиметра.

Развертывание – какие ошибки нельзя допускать?

Для получения как можно более чистой обработанной поверхности, а также, чтобы охлаждать инструмент во время работы, отверстия, которые были сделаны сверлом в стальном изделии, смазываются маслом из минералов. В случае же, если рабочая поверхность является медной, отверстие обрабатывают эмульсией, при алюминии – скипидаром, а если это латунь или бронза – отверстия оставляют без смазки, так как они развертываются в сухом состоянии.

Высокого качества процесса обрабатывания можно достичь, если в развертке имеется довольно много кромок, режущих металл. Именно благодаря этому инструментом можно снимать малый припуск. Ведь, снимая маленькую толщину металла, можно получить довольно высокую точность.

Частой ошибкой является неправильный выбор инструмента для развертывания: многие для этой цели выбирают вместо развертки зенкер. Это получистовой инструмент, не способный показать большую точность, у него меньше режущих заточек, да и вообще он предназначен для других целей. Поэтому к выбору инструмента нужно подходить внимательно. Да и в рамках одного вида инструментов следует грамотно выбирать тип.

Развертка коническая – особенности инструмента

Один из видов разверток, описываемый в этой статье, конический, применяют при работе, проходящей в более сложных условиях, чем те, когда работают цилиндрическими типами. Это связано с тем, что у последних небольшие режущие кромки, а припуск они снимают незначительный. Конические же развертки, напротив, для резки используют всю свою длину. В связи с этим, при работе с ними скорость работы и подача металла происходят медленнее, чем если бы использовался цилиндрический вид разверток.

Вышеупомянутые инструменты конического типа используют, чтобы развертывать конические отверстия. Для этого в комплекте находится три элемента: обдирочный, промежуточный и чистовой инструменты. Изготавливаются они для устройства конических резьб и конуса Морзе. Для качественного производства применяется сталь марок УЮА, У12А и прочие, а также пластинки, выполненные из твердых сплавов. Интересная особенность конических разверток заключается в следующем. У них на зубьях, расположенных прямолинейно, устраиваются поперечные прорези, через которые выводится снятая стружка, при этом они расположены не по всей длине зуба, что позволяет работать с инструментом, прилагая небольшие усилия.

Черновая развертка выполняется ступенчатой. При этом она обычно имеет вид отдельных зубьев, дробящих стружку на части.

Это приспособление может быть выполнено и в форме пирамиды с тремя, пятью или восемью гранями, с режущими ребрами. Конические развертки могут быть винтовыми, притом всего с одним или парой зубьев. Размер винтовых инструментов составляет в диаметре до 5 см, они широко используются при ремонте паровозов. Такой инструмент сегодня нашел достаточно большое применение в сфере строительства и ремонта благодаря своей долговечности, надежности, а также фактору, который заключается в том, что такой разверткой можно обрабатывать отверстия с большим припуском, а особенно при наличии в них отверстий шпоночного паза. К минусам можно отнести то, что для смены развертки, в случае надобности, может потребоваться немало времени.

Этапы работы с конической разверткой

Промежуточная коническая развертка устроена так: её прорези делаются меньше, да и профиль их отличается. Если же упомянуть чистовую развертку, то на ней никаких канавок для лома стружек нет. Ступени на зубьях расположены по винтовой линии на конусе, угол которого равен значению, отмеченному на наклоне конуса Морзе. Поэтому направление, по которому идет резьба, совпадает с тем, в какую сторону производится резание.

После предварительной обработки отверстия другим инструментом берется развертка, которой цилиндрическое отверстие мы превращаем в коническое или же с помощью которой проводим калибровку. Зубья на ней, число которых колеблется от трех до восьми (зависит от размеров конуса для обработки), сзади имеют тыльную поверхность. Шаг этого инструмента, как правило, делается равным предыдущим шагам и является равномерным.

Конические развертки, применяемые для кранов и инструментов, обычно изготавливают по одной для каждого отверстия. Их элементы конструктивного плана выбираются по такому же принципу, как и в случае с цилиндрическими развертками. Для отверстий, конус которых планируется делать малым (от 1/50 до 1/30) применяют лишь одну развертку. Если же конусность решают сделать большой, в этом случае необходимо срезать большой и неравномерный припуск. Из-за этого развертывание делается при помощи комплекта инструментов, состоящего из трех экземпляров.

Принцип черновой развертки напоминает суть работы зенкера, упомянутого выше. В ней есть режущая ступенчатая кромка, благодаря которой получается ступенчатое отверстие. После неё используется промежуточный тип. Взглянув на этот инструмент, легко увидеть канавки для разделения стружек, они сделаны в виде резьбы. Последней применяется чистовая развертка, снимающая мелкую стружку всей своей кромкой, удобно устроенной для резания. Её зубья острые, имеют один и тот же шаг. Скорость, с которой режут металл при развертывании с использованием конических инструментов, – 6-10 м/минуту. Для измерения поверхности применяют такие приборы, как угломеры, калибры и шаблоны.

Оцените статью: Поделитесь с друзьями!

remoskop.ru

Развертка конуса

Полный конус вращения (рис.5.7) развертывается в сектор с углом =360 хR/Lи радиусомL, гдеR- радиус основания конуса,L– длина образующей конуса. Разделив уголна число образующих, отмечаем на развертке точки 0, 1, 2… (вписываем пирамиду). При построении развертки усеченного конуса на каждой образующей откладываем действительную величину соответствующего ее отрезка, например1К. Для этого предварительно находим действительную длину отрезка по проекции12К2, повернув образующую12S2вокруг оси конуса до крайнего (фронтального) положения12*S2. Отрезок12*К2*дает1К. Точки, полученные на развертке, соединяем плавной кривой. На рис.5.8. представлена развертка боковой поверхности к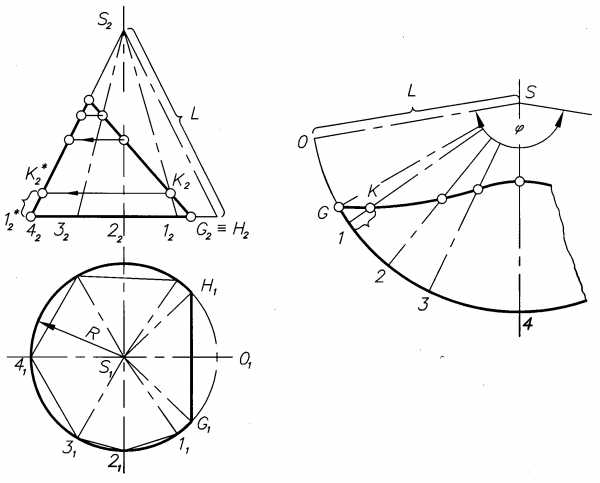онуса.

Рис.5.7.

Пересечение плоскостью сферы, тора

На рис.5.8. показан простейший случай усечения сферы плоскостями, параллельными плоскостям проекций. Получившиеся при этом окружности проецируются в виде прямых или в виде окружностей. Так, плоскость  пересекается со сферой по окружности диаметра 2-2*. Фронтальная проекция этой окружности – прямая2222*, а профильная проекция – окружность. Радиус этой окружности равен половине расстояния2222*. Плоскостьпересекается со сферой по окружности1-1*,которая проецируется в виде окружности на горизонтальную плоскость проекции.

На рис.5.9 приведен пример усеченного тора плоскостью  (по кривой четвертого порядка).

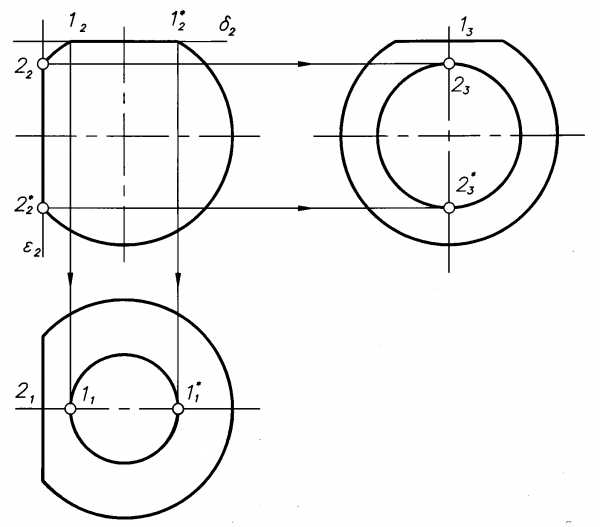
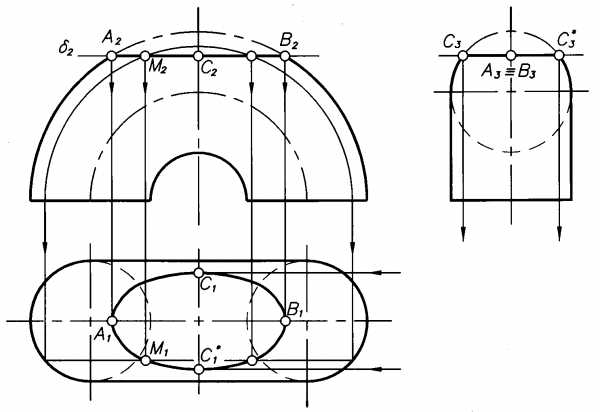
Рис.5.8. Рис.5.9.

Отметив опорные точки А, В и С, определяем промежуточную точкуМс помощью окружностей (параллелей). На проекции плоскости2 (на фронтальной проекции линии пересечения) задаемся проекциейМ2произвольной точкиМи проводим окружность на торе так, чтобы ее фронтальная проекция прошла через проекцию точкиМ2. Построив горизонтальную проекцию этой окружности – прямую линию, находим на ней проекциюМ1. Наносим проекции симметричных точек.

Глава 6. Взаимное пересечение поверхностей

Как правило, детали представляют собой комбинации пересекающихся геометрических элементов, ограниченных плоскостями и кривыми поверхностями. При разработке чертежа линии пересечения поверхностей должны быть построены (за исключением случаев допускаемых упрощений). При построении разверток поверхностей также необходимо точное построение их линий пересечения. Задача построения линии взаимного пересечения поверхностей заключается в нахождении точек, принадлежащих одновременнопересекающимся поверхностям.

Пересечение соосных поверхностей вращения

Наиболее простым случаем является пересечение соосных поверхностей вращения, т.е. поверхностей, имеющих общую ось. Поверхности в этом случае пересекаются по окружностям, которые могут проецироваться в прямые линии, когда ось вращения параллельна плоскости проекций (рис.6.1,а). В случае плавного очертания, характерного, например, для литых деталей (рис.6.1,б), проекцию линии пересечения проводят тонко, не доводя до проекции образующей.

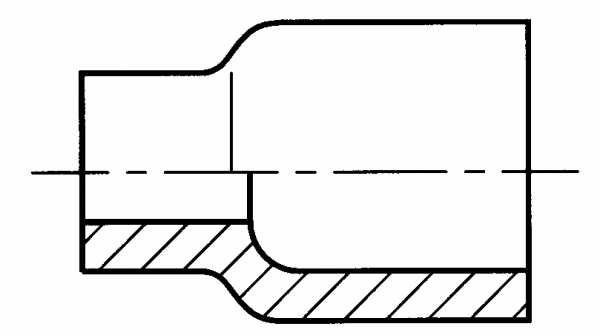
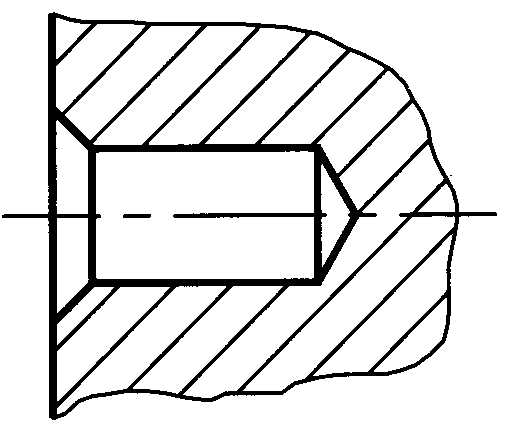
а б

Рис.6.1.

studfiles.net