Система допусков и посадок

Слово термин происходит от латинского слова terminus, что значит предел граница.

Размер – числовое значение линейной величины в выбранных единицах измерения.

Действительный размер – размер элемента, установленный измерением
с допускаемой погрешностью.

Номинальные и предельные размеры

Предельные размеры – два предельно допустимых размера элемента, между
которыми должен находиться (или которым может быть равен) действительный размер.

Наибольший предельный размер – наибольший допустимый размер элемента.

Наименьший предельный размер – наименьший допустимый размер элемента.

Номинальный размер – размер, относительно которого определяются отклонения.

Отклонение – арифметическая разность между размером и соответствующим номинальным размером.

Действительное отклонение – арифметическая разность между действительным и соответствующим номинальным размерами.

Предельное отклонение – арифметическая разность между предельным и
соответствующим номинальным размерами. Различают верхнее и нижнее предельные
отклонения.

Нулевая линия – линия, соответствующая номинальному размеру, от которой
откладываются отклонения размеров при графическом изображении полей допусков и
посадок. Если нулевая линия расположена горизонтально, то положительные отклонения
откладываются вверх от нее, а отрицательные – вниз.

Верхнее отклонение ES, es – арифметическая разность между наибольшим предельным и соответствующим номинальным размерами.

Примечание:

ES – верхнее отклонение отверстия; es – верхнее отклонение вала.

Нижнее отклонение EI, ei – арифметическая разность между наименьшим предельным и соответствующим номинальным размерами.

Примечание:

EI – нижнее отклонение отверстия; ei – нижнее отклонение вала.

Основное отклонение – одно из двух предельных отклонений (верхнее или
нижнее), определяющее положение поля допуска относительно нулевой линии. В данной
системе допусков и посадок основным является отклонение, ближайшее к нулевой линии.

Поля допусков и посадок

Допуск – Т – англ.tolerance – разность между наибольшим и наименьшим предельными размерами или разность между верхним и нижним отклонениями.

Примечание:

Допуск – это абсолютная величина без знака.

Стандартный допуск – IT – англ. Internal tolerance – любой из допусков, устанавливаемых данной системой допусков и посадок.

Примечание:

В дальнейшем в стандарте под термином «допуск» понимается
«стандартный допуск».

Поле допуска – поле, ограниченное наибольшим и наименьшим предельными
размерами и определяемое величиной допуска и его положением относительно
номинального размера. При графическом изображении поле допуска заключено между
двумя линиями, соответствующими верхнему и нижнему отклонениям относительно
нулевой линии .

Примечание:

i – единица допуска для номинальных размеров до 500 мм,
I – единица допуска для номинальных размеров свыше 500 мм.

Квалитет – лат. qualitas – качество – совокупность допусков, рассматриваемых как
соответствующие одному уровню точности для всех номинальных размеров.

Единица допуска i, I – множитель в формулах допусков, являющийся функцией
номинального размера и служащий для определения числового значения допуска.

Вал – термин, условно применяемый для обозначений наружных элементов деталей, включая и нецилиндрические элементы.

Отверстие – термин, условно применяемый для обозначения внутренних элементов деталей, включая и нецилиндрические элементы.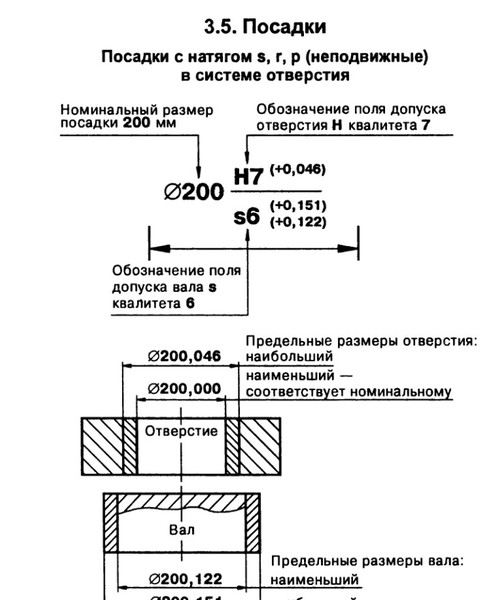

Основной вал – вал, верхнее отклонение которого равно нулю.

Основное отверстие – отверстие, нижнее отклонение которого равно нулю.

Предел максимума материала – термин, относящийся к тому из предельных
размеров, которому соответствует наибольший объем материала, т.е. наибольшему
предельному размеру вала или наименьшему предельному размеру отверстия.
Примечание. Применявшийся ранее термин «проходной предел» использовать не
рекомендуется.

Предел минимума материала – термин, относящийся к тому из предельных
размеров, которому соответствует наименьший объем материала, т.е. наименьшему
предельному размеру вала или наибольшему предельному размеру отверстия.
Примечание. Применявшийся ранее термин «непроходной предел» использовать не
рекомендуется.

Посадка – характер соединения двух деталей, определяемый разностью их
размеров до сборки.

Номинальный размер посадки – номинальный размер, общий для отверстия и
вала, составляющих соединение.

Допуск посадки – сумма допусков отверстия и вала, составляющих соединение.

Зазор – разность между размерами отверстия и вала до сборки, если размер
отверстия больше размера вала.

Зазор между отверстием и валом

Натяг – разность между размерами вала и отверстия до сборки, если размер вала больше размера отверстия.

Натяг между отверстием и валом

Посадка с зазором – посадка, при которой всегда образуется зазор в соединении,
т.е. наименьший предельный размер отверстия больше наибольшего предельного размера вала или равен ему. При графическом изображении поле допуска отверстия расположено над полем допуска вала.

Посадка с натягом – посадка, при которой всегда образуется натяг в соединении,
т. е. наибольший предельный размер отверстия меньше наименьшего предельного размера вала или равен ему. При графическом изображении поле допуска отверстия расположено под полем допуска вала.

Переходная посадка – посадка, при которой возможно получение как зазора, так и
натяга в соединении, в зависимости от действительных размеров отверстия и вала. При
графическом изображении поля допусков отверстия и вала перекрываются полностью или частично.

Переходная посадка

Наименьший зазор – разность между наименьшим предельным размером
отверстия и наибольшим предельным размером вала в посадке с зазором.

Наибольший зазор – разность между наибольшим предельным размером
отверстия и наименьшим предельным размером вала в посадке с зазором или в переходной посадке.

Наименьший натяг – разность между наименьшим предельным размером вала и
наибольшим предельным размером отверстия до сборки в посадке с натягом.

Наибольший натяг – разность между наибольшим предельным размером вала и
наименьшим предельным размером отверстия до сборки в посадке с натягом или в
переходной посадке.

Посадки в системе отверстия – посадки, в которых требуемые зазоры и натяги
получаются сочетанием различных полей допусков валов с полем допуска основного
отверстия.

Посадки в системе вала – посадки, в которых требуемые зазоры и натяги
получаются сочетанием различных полей допусков отверстий с полем допуска основного
вала.

Наименьший и наибольший зазор

Наименьший и наибольший натяг

Допуски размеров, отклонения, посадки и квалитеты.



Основные понятия о допусках и посадках

Механизмы машин и приборов состоят из деталей, совершающих в процессе работы определенные относительные движения или соединенных неподвижно. Детали, в той или иной степени взаимодействующие между собой в механизме, называют сопряженными.


Абсолютно точное изготовление любой детали невозможно, как невозможно и измерить ее абсолютный размер, поскольку точность любого измерения ограничена возможностями средств измерения на данном этапе научно-технического прогресса, при этом предела этой точности не существует. Впрочем, выполнение деталей механизмов с наибольшей точностью зачастую нецелесообразно, в первую очередь — с экономической точки зрения, поскольку высокоточные изделия значительно дороже в изготовлении, а для нормального функционирования в механизме вполне достаточно выполнить деталь с меньшей точностью, т. е. дешевле.

Производственный опыт показал, что задачу выбора оптимальной точности можно решить установлением для каждого размера детали (особенно для сопрягаемых ее размеров) пределов, в которых может колебаться ее действительный размер; при этом исходят из того, что узел, в который входит деталь, должен соответствовать своему назначению и не терять работоспособность в требуемых условиях функционирования с необходимым ресурсом.

Рекомендации по выбору предельных отклонений размеров деталей разработаны на основании многолетнего опыта изготовления и эксплуатации различных механизмов и приборов и научных исследований, и изложены в единой системе допусков и посадок (ЕСДП СЭВ). Допуски и посадки, установленные ЕСДП СЭВ, могут быть осуществлены по системам отверстия или вала.

Рассмотрим основные понятия из этой системы.

***

Номинальным называют основной размер, получаемый из расчета на прочность, жесткость или выбираемый конструктивно и проставляемый на чертеже. Проще говоря, номинальный размер детали получен конструкторами и разработчиками расчетным путем (исходя из требований прочности, жесткости и т. п.) и указывается на чертеже детали в виде основного размера.

Номинальный размер соединения является общим для отверстия и вала, составляющих соединение. По номинальным размерам выполняют в том или ином масштабе чертежи деталей, сборочных единиц и приборов.

Для унификации и стандартизации установлены ряды номинальных размеров (ГОСТ 8032-84 «Предпочтительные числа и ряды предпочтительных чисел»). Полученный расчетом или выбранный размер следует округлять до ближайшего значения из стандартного ряда. Это особенно относится к размерам деталей, получаемым стандартным или нормализованным инструментом, или присоединительным по отношению к другим стандартным деталям или узлам.

Для сокращения номенклатуры применяемого в производстве режущего и измерительного инструмента в первую очередь рекомендуется применять размеры, оканчивающиеся на 0 и 5, а затем — на 0; 2; 5 и 8.

Размер, полученный в результате измерения детали с наибольшей возможной точностью, называют действительным.

Не следует путать действительный размер детали с ее абсолютным размером.

Абсолютный размер – реальный (фактический) размер детали; его невозможно измерить никакими сверхточными средствами измерения, поскольку всегда будет присутствовать погрешность, обусловленная, в первую очередь, уровнем развития науки, техники и технологий. Кроме того, любое материальное тело при температуре выше абсолютного нуля «дышит» — на его поверхности постоянно перемещаются микрочастицы, молекулы и атомы, отрываясь от тела и возвращаясь обратно. Поэтому, даже имея в распоряжении сверхточные средства измерений, абсолютный размер детали определить невозможно; можно лишь говорить о реальном размере в бесконечно малый отрезок (момент) времени.

Вывод очевиден — абсолютный размер детали (как и любого тела) — понятие абстрактное.

Размеры, между которыми может находиться действительный размер изготовленной детали, называют предельными, при этом различают наибольший и наименьший предельные размеры.

Выполненная в интервале между предельными размерами деталь считается годной. Если же ее размер выходит за предельные ограничения – она считается браком.

По предельным размерам устанавливают тип соединения деталей и допустимую неточность их изготовления.

Для удобства на чертежах указывают номинальный размер детали, а каждый из двух предельных размеров определяют по его отклонению от этого размера. Величину и знак отклонения получают в результате вычитания номинального размера из соответствующего предельного размера.

Разность между наибольшим предельным и номинальным размерами называется верхним отклонением (обозначается es или ES), разность между наименьшим предельным и номинальным — нижним отклонением (обозначается ei или EI).

Верхнее отклонение соответствует наибольшему предельному размеру, а нижнее — наименьшему.

Все сопрягаемые (взаимодействующие) в механизме детали подразделяют на две группы – валы и отверстия.

Вал обозначает наружный (охватываемый) элемент детали. При этом вал не обязательно должен иметь круглую форму: в понятие «вал» входит, например, шпонка, а шпоночный паз в этом случае называют «отверстием». Основным называют вал, верхнее отклонение которого равно нулю.

Размеры вала на схемах и при расчетах обозначаются строчными (маленькими) буквами: d, dmax, dmin, es, ei и т. д.

Отверстие обозначает внутренний (охватывающий) элемент детали. Как и в случае с валом, отверстие не обязательно должно быть круглым – его форма может быть любой. Основным называют отверстие, нижнее отклонение которого равно нулю.

Размеры отверстия на схемах и при расчетах обозначаются прописными (заглавными) буквами: D, Dmax, Dmin, ES, EI и т. д.

Допуском (Т) называется разность между наибольшим и наименьшим предельными размерами детали. Т. е. допуск – это интервал между предельными размерами, в пределах которого деталь не считается браком.

Допуск на размер вала обозначают Тd, отверстия – TD. Очевидно, что чем больше допуск на размер, тем легче изготовить деталь.

Допуск на размер детали может быть определен, как разность между предельными размерами или как сумма предельных отклонений:

TD(d) = D(d)max – D(d)min = ES(es) + EI(ei),

при этом следует учитывать знаки предельных отклонений, поскольку допуск на размер детали всегда положителен (не может быть меньше нуля).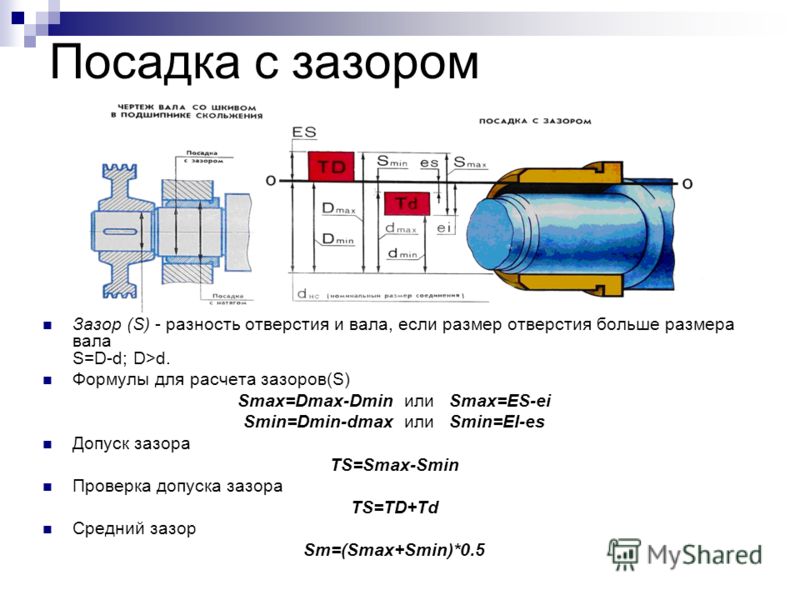

***

Посадки

Характер соединения, определяемый разностью между охватывающим и охватываемым размером, называется посадкой.

Положительная разность между диаметрами отверстия и вала называется зазором (обозначается буквой S), а отрицательная – натягом (обозначается буквой N).

Иными словами, если диаметр вала меньше диаметра отверстия – имеет место зазор, если же диаметр вала превышает диаметр отверстия – в сопряжении присутствует натяг.

Зазор определяет характер взаимной подвижности сопряженных деталей, а натяг — характер их неподвижного соединения.

В зависимости от соотношения действительных размеров вала и отверстия различают подвижные посадки — с зазором, неподвижные посадки — с натягом и переходные посадки, т. е. посадки, в которых может присутствовать и зазор, и натяг (в зависимости от того, какие отклонения имеют действительные размеры сопрягаемых деталей от номинальных размеров).

Посадки, в которых обязательно присутствует зазор, называют посадками с гарантированным зазором, а посадки, в которых обязателен натяг – с гарантированным натягом.

В первом случае так выбирают предельные размеры отверстия и вала, чтобы в сопряжении был гарантированный зазор.

Разность между наибольшим предельным размером отверстия (Dmax) и наименьшим предельным размером вала (dmin) определяет наибольший зазор (Smax):

Smax = Dmax – dmin.

Разность между наименьшим предельным размером отверстия (Dmin) и наибольшим предельным размером вала (dmax) — наименьший зазор (Smin):

Smin = Dmin – dmax.

Действительный зазор будет находиться между указанными пределами, т. е. между максимальным и минимальным зазором. Зазор необходим для обеспечения подвижности соединения и размещения смазки. Чем выше число оборотов и выше вязкость смазки, тем больше должен быть зазор.

В посадках с натягом так выбирают предельные размеры вала и отверстия, чтобы в сопряжении был гарантированный натяг, ограниченный минимальным и максимальным значениями – Nmax и Nmin:

Nmax = dmax – Dmin,       Nmin = dmin – Dmax.

Переходные посадки могут дать зазор или натяг небольшой величины. До изготовления деталей нельзя сказать, что будет в сопряжении. Это становится ясным только при сборке. Зазор не должен превышать величины наибольшего зазора, а натяг — величины наибольшего натяга. Переходные посадки применяются в том случае, если необходимо обеспечить точное центрирование отверстия и вала.

Всего в ЕСДП СЭВ предусмотрено 28 типов основных отклонений для валов и столько же для отверстий. Каждый из них обозначается строчной латинской буквой (ГОСТ 2.304 — 81), если отклонение относится к валу, или прописной, если отклонение относится к отверстию.

Буквенные обозначения основных отклонений приняты в алфавитном порядке, начиная от отклонений, обеспечивающих самые большие зазоры в соединении. Сочетанием различных отклонений вала и отверстия можно получить посадки разного характера (зазор, натяг или переходная).

***

Посадки в системе отверстия и системе вала

Посадки, установленные ЕСДП СЭВ, могут быть осуществлены по системам отверстия или вала.

Система отверстия характеризуется тем, что в ней для всех посадок предельные размеры отверстия остаются постоянными, а посадки осуществляются соответствующим изменением предельных размеров вала (т. е. вал подгоняется по отверстию). Размер отверстия называется основным, а размер вала — посадочным.

Система вала характеризуется тем, что в ней для всех посадок предельные размеры вала остаются постоянными, а посадки осуществляются изменением отверстия (т. е. отверстие подгоняется по размеру вала). Размер вала называется основным, а отверстия — посадочным.

На промышленных предприятиях в основном применяют систему отверстия, так как она требует меньшего количества режущего и измерительного инструмента, т. е. более экономична. Кроме того, технологически удобнее подгонять вал под отверстие, а не наоборот, поскольку удобнее производить обработку и контрольные измерения внешней поверхности, а не внутренней.

Систему вала, как правило, применяют для наружных колец шарикоподшипников и в тех случаях, когда на гладкий вал насаживают несколько деталей с различными посадками.

В машиностроении наиболее распространены посадки, расположенные в порядке убывания натяга и возрастания зазора: прессовая (Пр), легкопрессовая (Пл), глухая (Г), тугая (Т), напряженная (Н), плотная (П), скольжения (С), движения (Д), ходовая (X), легкоходовая (Л), широкоходовая (Ш).

Прессовые посадки дают гарантированный натяг. Глухая, тугая, напряженная и плотная посадки являются переходными, а остальные имеют гарантированный зазор.

Для скользящей посадки гарантированный зазор равен нулю.

Для оценки точности соединений (посадок) пользуются понятием допуска посадки, под которым понимается разность между наибольшим и наименьшим зазорами (в посадках с зазором) или наибольшим и наименьшим натягами (в посадках с натягом). В переходных посадках допуск посадки равен разности между наибольшим и наименьшим натягами или сумме наибольшего натяга и наибольшего зазора.

Допуск посадки равен также сумме допусков отверстия и вала.

***



Квалитеты

Совокупность допусков, соответствующих одинаковой степени точности для всех номинальных размеров, называется квалитетом (I). Иными словами, квалитет – степень точности, с которой выполнена деталь, при этом учитывается размер этой детали.

Очевидно, что если выполнить с одинаковым допуском очень большую и очень маленькую деталь, то относительная точность изготовления большой детали будет выше. Поэтому системой квалитетов принимается в расчет то, что (при одинаковых допусках) отношение величины допуска к номинальному размеру у большой детали будет меньше, чем отношение допуска к номинальному размеру маленькой детали (рис. 2), т. е. условно большая деталь изготовлена точнее относительно своих размеров. Если, например, для вала с номинальным диаметром 3 метра миллиметровое отклонение от размера можно считать незначительным, то для вала диаметром 10 мм такое отклонение будет очень ощутимым.

Введение системы квалитетов позволяет избежать такой путаницы, поскольку точность изготовления деталей привязывается к их размерам.

По ЕСДП СЭВ квалитеты стандартизованы в виде 19 рядов. Каждый квалитет обозначается порядковым номером 01; 0; 1; 2; 3;…; 17, возрастающим с увеличением допуска.

Два самых точных квалитета — 01 и 0.

Ссылка на допуски по квалитетам ЕСДП СЭВ может быть сделана сокращенно буквами IT «Международный допуск» с номером квалитета.

Например, IT7 означает допуск по 7-му квалитету.

В системе СЭВ для обозначения допусков с указанием квалитетов применяются следующие условные обозначения:

• Используются буквы латинского алфавита, при этом отверстия определяются прописными буквами, а валы — строчными.
• Отверстие в системе отверстия (основное отверстие) обозначается буквой Н и цифрами — номером квалитета. Например, Н6, Н11 и т. д.
• Вал в системе отверстия обозначается символом посадки и цифрами — номером квалитета. Например, g6, d11 и т. д.
• Сопряжение отверстия и вала в системе отверстия обозначается дробно: в числителе — допуск отверстия, в знаменателе — допуск вала.

***

Графическое изображение допусков и посадок

Для наглядности часто используют графическое изображение допусков и посадок с помощью, так называемых, полей допусков (см. рис. 3).

Построение выполняется следующим образом.

От горизонтальной линии, условно изображающей поверхность детали при ее номинальном размере, откладывают предельные отклонения в произвольно выбранном масштабе. Обычно на схемах величины отклонений указывают в микронах, но можно строить поля допусков и в миллиметрах, если отклонения достаточно большие.

Линия, которая при построении схем полей допусков соответствует номинальному размеру и служит началом отсчета отклонений размеров, называется нулевой (0-0).

Поле допуска — поле, ограниченное верхним и нижним отклонениями, т. е. при графическом изображении поля допусков показывают зоны, которые ограничены двумя линиями, проведенными на расстояниях, соответствующих верхнему и нижнему отклонению в избранном масштабе.

Очевидно, что поле допуска определяется величиной допуска и его положением относительно номинального размера.

На схемах поля допусков имеют вид прямоугольников, верхние и нижние стороны которых параллельны нулевой линии и отображают предельные отклонения, а боковые стороны в избранном масштабе соответствует допуску размера.

На схемах указывают номинальный D и предельные (Dmax, Dmin, dmax, dmin) размеры, предельные отклонения (ES, EI, es, ei) поля допусков и другие параметры.

Предельное отклонение, которое ближе к нулевой линии, называют основным (верхним или нижним). Оно определяет положение поля допусков относительно нулевой линии. Для полей допусков, расположенных ниже нулевой линии, основным является верхнее отклонение.

Для полей допусков, расположенных выше нулевой линии, основным является нижнее отклонение.

Принцип образования полей допусков, принятый в ЕСДП, допускает сочетание любых основных отклонений с любыми квалитетами. Например, можно образовать поля допусков а11, u14, с15 и другие, не установленные в стандарте. Исключение представляют основные отклонения J и j, которые заменяются основными отклонениями Js, и js.

Использование всех основных отклонений и квалитетов позволяет получить 490 полей допусков для валов и 489 для отверстий. Такие широкие возможности образования полей допусков позволяют применять ЕСДП в различных специальных случаях. Это является ее существенным достоинством. Однако на практике использование всех полей допусков неэкономично, так как вызовет чрезмерное разнообразие посадок и специальной технологической оснастки.

При разработке национальных систем допусков и посадок на базе систем ИСО из всего многообразия полей допусков отбирают только те поля, которые обеспечивают потребности промышленности страны и ее внешнеэкономические связи.

• h и H — верхнее и нижнее отклонения вала и отверстия, равные нулю (допуски с основными отклонениями h и H приняты для основных валов и отверстий).
• а — h (А — H) — отклонения, образующие поля допусков при посадках с зазорами.
• js — n (Js — N) — отклонения, образующие поля допусков переходных посадок.
• p – zc (P — ZC) — отклонения, образующие поля допусков посадок с натягом.

Схематически основные отклонения показаны на Рис. 4.

Поле допуска в ЕСДП СЭВ образуется сочетанием одного из основных отклонений с допуском по одному из квалитетов. В соответствии с этим поле допуска обозначается буквой основного отклонения и номером квалитета, например 65f6; 65e11 — для вала; 65Р6; 65H7 — для отверстия.

Основные отклонения зависят от номинальных размеров деталей и остаются постоянными для всех квалитетов. Исключение составляют основные отклонения отверстий J, К, М, N и валов j и k, которые при одинаковых номинальных размерах, в разных квалитетах имеют различные значения. Поэтому на схемах поля допусков с отклонениями J, К, М, N, j, k, обычно разделены на части и показаны ступенчатыми.

Специфичны поля допусков типа js6, Js8, Js9 и т.д. Они фактически не имеют основного отклонения, поскольку расположены симметрично относительно нулевой линии. По определению основное отклонение – это отклонение ближайшее к нулевой линии. Значит, оба отклонения таких специфических полей допусков могут быть признаны основными, что недопустимо.

Особое значение имеют основные отклонения H и h, которые равны нулю (рисунок). Поля допусков с такими основными отклонениями расположены от номинала «в тело» детали; их называют полями допусков основного отверстия и основного вала.

Обозначения посадок строятся как дроби, причем в числителе всегда находится обозначение поля допуска охватывающей поверхности (отверстия), а в знаменателе – поля допуска охватываемой (вала).

При выборе квалитета соединения и вида посадки конструктору следует учитывать характер сопряжения, эксплуатационные условия, наличие вибрации, срок службы, колебания температуры и стоимость изготовления.

Квалитет и вид посадки рекомендуется выбирать по аналогии с теми деталями и узлами, работа которых хорошо известна, или руководствоваться рекомендациями справочной литературы и нормативных документов (ОСТов).

В соответствии с квалитетом посадки выбирается чистота поверхности сопрягаемых деталей.

Допуски и посадки установлены для четырех диапазонов номинальных размеров:

• малый — до 1 мм;
• средний — от 1 до 500 мм;
• большой — от 500 до 3150 мм;
• очень большой — от 3150 до 10 000 мм.

Средний диапазон является наиболее важным, поскольку применяется значительно чаще.

***

Обозначение допусков на чертежах

Указания и обозначения на чертежах предельных отклонений формы и расположения поверхностей регламентируются ГОСТ 2.308-79, который предусматривает для этих целей специальные знаки и символы.

С основными положениями этого стандарта, используемыми знаками и символами для обозначения предельных отклонений, можно ознакомиться в этом документе (формат WORD, 400 кБ).

***

Пример решения задачи на расчет допусков и посадок подшипникового соединения



Главная страница

• Страничка абитуриента

Дистанционное образование

• Группа ТО-81
• Группа М-81
• Группа ТО-71

Специальности

• Ветеринария
• Механизация сельского хозяйства
• Коммерция
• Техническое обслуживание и ремонт автотранспорта

Учебные дисциплины

• Инженерная графика
• МДК.01.01. «Устройство автомобилей»
•    Карта раздела
•       Общее устройство автомобиля
•       Автомобильный двигатель
•       Трансмиссия автомобиля
•       Рулевое управление
•       Тормозная система
•       Подвеска
•       Колеса
•       Кузов
•       Электрооборудование автомобиля
•       Основы теории автомобиля
•       Основы технической диагностики




• Основы гидравлики и теплотехники
• Метрология и стандартизация
• Сельскохозяйственные машины
• Основы агрономии
• Перевозка опасных грузов
• Материаловедение
• Менеджмент
• Техническая механика
• Советы дипломнику

Олимпиады и тесты

• «Инженерная графика»
• «Техническая механика»
• «Двигатель и его системы»
• «Шасси автомобиля»
• «Электрооборудование автомобиля»

Определение

— Что такое верхний предел и нижний предел?

спросил
9 лет, 4 месяца назад

Изменено
30 дней назад

Просмотрено
38 тысяч раз

$\begingroup$

Я просмотрел статью в Википедии, но она кажется тарабарщиной. Единственное, что я смог извлечь из этого, — это концепция инфимума (наибольшая нижняя граница) и супремум (наименьшая верхняя граница), поскольку я изучил их ранее во вступительном курсе дискретной математики.

Нижний предел последовательности ($x_n$) определяется как

$\displaystyle\liminf_{n\to\infty}x_n := \lim_{n\to\infty}\Big(\inf_{m\geq n}x_m\Big)$

или

$\displaystyle\liminf_{n\to\infty}x_n := \sup_{n\geq 0}\,\inf_{m\geq n}x_m=\sup\{\,\inf\{\,x_m: m\geq n\,\}:n\geq 0\,\}.$

Аналогично, верхний предел ($x_n$) определяется как

$\displaystyle\limsup_{n\to\infty}x_n := \lim_{n\to\infty}\Big(\sup_{m\geq n}x_m\Big)$

или

$\displaystyle\limsup_{n\to\infty}x_n := \inf_{n\geq 0}\,\sup_{m\geq n}x_m=\inf\{\,\sup\{\,x_m: m\geq n\,\}:n\geq 0\,\}.$

Кто-нибудь может привести примеры его использования и почему он используется в этом контексте?

• определение
• limsup-and-liminf

$\endgroup$

4

$\begingroup$

Я обнаружил, что некоторые учащиеся с трудом понимают обычные определения верхнего и нижнего пределов, потому что эти определения сочетают в себе понятия пределов, супремы и инфимы, которые учащиеся, возможно, усвоили совсем недавно и не полностью усвоили. . Для таких студентов я хотел бы дать следующие альтернативных определений , эквивалентных обычным, но не содержащих слов «предел», «супремум» и «инфимум». (Нет также абсолютных значений или видимых $\varepsilon$.)

Число $t$ является пределом, превосходящим последовательность $\langle a_n\rangle$, если выполняются следующие два условия:

Аналогично, число $t$ является нижним пределом последовательности $\langle a_n\rangle$, если выполняются оба следующих условия:

Могут быть полезны два дополнительных замечания:

1. Определение lim inf получается из определения lim sup простым обращением всех неравенств.

2. Определения можно легко расширить до $\pm\infty$ вместо чисел $t$. Просто примите соглашение, что даже в этом случае $s$ относится к реальным числам, все из которых равны $>-\infty$ и $<+\infty$.

$\endgroup$

0
9n$ для любого $L’>L$, и это сходится (к $\frac1{1-|L’x|}$), если $|L’x|<1$, и при подходящем выборе $L'$ мы получаем сходимость, когда $|Lx|<1$. Но если предела не существует, мы должны использовать $\limsup$, так что у нас есть sub -последовательность, сходящаяся к некоторому $L$, и мы можем выбрать такую ​​большую подпоследовательность, что все остальные члены $\sqrt[n]{ |a_n|}$ меньше $L$. Эти малые члены не мешают сходимости, если $|xL|<1$. И все же, поскольку наша подпоследовательность имеет бесконечно много членов, этого достаточно, чтобы испортить сходимость при $|xL|>1$.

$\endgroup$

1

$\begingroup$

Самый интуитивный способ, на мой взгляд, состоит в том, чтобы попытаться понять, что он делает с изображением (кредит пользователя Wikimedia Commons Eigenjohnson):

Мы знаем, что максимума или минимума последовательности может не быть, но верхняя и нижняя грани всегда существуют (если последовательность ограничена; если нет, мы можем рассматривать верхнюю/нижнюю грань в расширенной вещественной строке как $\pm \infty$ ). Однако верхняя/нижняя граница описывает верхнюю/нижнюю границу по всей последовательности , поэтому не дает нам информации о конце последовательности или о том , как последовательность в конечном итоге ведет себя . На рисунке верхняя грань по всей последовательности $(x_n)$ составляет около 1,75 для ранних значений в последовательности, но это не говорит нам о более поздних членах ($x_n$ для больших $n$), которые, по-видимому, имеют супремум 1,0.

$\liminf$ и $\limsup$, с другой стороны, говорят нам о инфимуме и супремуме, когда $n$ стремится к бесконечности, и мы рассматриваем более поздние и более поздние члены $x_n$. Одно определение (которое я считаю наиболее интуитивным): $$\limsup_{n \to \infty} x_n = \lim_{n \to \infty} \sup_{m \ge n} x_m$$

По характеру этого определения мы рассматриваем верхнюю грань по хвосту последовательности значений $x_m$ или более поздней, то есть $(x_m)_{m \gen}$, и имея предел как $m \to \infty$ мы рассматриваем более поздние хвосты последовательности. Это отражает понятие лучших границ того, как последовательность в конечном итоге ведет себя для гораздо более поздних членов . Еще одна приятная особенность этого определения заключается в том, что $\limsup$ выглядит как $\lim$ $\sup$, и поэтому мы можем помнить, с чем работаем.

Другое определение: $$\limsup_{n \to \infty} x_n = \sup \mathscr L$$

, где $\mathscr L$ — множество предельных точек последовательности, то есть все $l \in \mathbb R$ такое, что существует подпоследовательность $(x_{n_k})$, сходящаяся к $l$. (См. Ответ Педро Тамароффа для более формального определения и объяснения). Это определение также отражает представление о том, как в конечном итоге ведет себя последовательность, принимая во внимание все предельные точки, которые по своей природе учитывают, как члены $x_{n_k}$ ведут себя при стремлении $n$ к бесконечности. Доказательство эквивалентности этих двух определений (см. Два определения $\limsup$, Доказательство эквивалентности двух определений $\limsup$ и $\liminf$) проливает свет на то, что именно делают эти определения.

Третья характеристика (в ответе Андреаса Бласса) полезна для доказательств и говорит следующее: если $l = \limsup_{n \to \infty} x_n$, то для всех $\epsilon > 0$

• существует $N \in \mathbb N$ такое, что для всех $n \ge N$, $x_n \le l + \epsilon$ и
• $x_n \ge l — \epsilon$ для бесконечного множества $n \in \mathbb N$.

Эту характеристику можно доказать из второго определения, используя определение предела и супремума (чтобы доказать, предположим противное для каждой части и получим противоречие. Первая часть использует теорему Больцано-Вейерштрасса для нахождения сходящейся подпоследовательности). Работа с этим определением и доказательство его эквивалента второму определению (с предельными точками) дает представление о том, что означает $\limsup$, а явное использование $\epsilon$ делает его удобным для доказательств, где мы хотим работать с явными границами. 9*:x\text{ является предельной точкой }\langle a_n\rangle\}$$
Тогда $\mathscr L$ непусто при любом выборе $\langle a_n\rangle$.

P Сначала предположим, что $\langle a_n\rangle$ ограничено. Согласно Больцано Вейерштрассу, существует сходящаяся подпоследовательность $\langle a_{n_k}\rangle$ последовательности $\langle a_n\rangle$ такая, что $\lim\limits_{k\to\infty}a_{n_k}=\ell $ для некоторый $\ell\in\Bbb R$. Таким образом, $\ell\in\mathscr L$. Теперь предположим, что $\langle a_n\rangle$ неограничен. Можно считать его неограниченным сверху. Тогда по определению для каждого $k\in \Bbb N$ существует $n_k$ такое, что $a_{n_k}\geq k$. Отсюда следует $\lim\limits_{k\to\infty}a_{n_k}=+\infty$, поэтому $+\infty\in\mathscr L$.

Предположим, что с этого момента последовательность ограничена.

DEF Пусть $\langle a_k\rangle$ — последовательность в $\Bbb R$. Определим для каждого $n\in \Bbb N$ соответствующие последовательности $$\overline{a_n}=\sup \langle a_k:k\geq n\rangle$$ $$\underline{a_n}=\inf \langle a_k :k\geq n\rangle$$ и затем закрытые интервалы $$A_n=\left[\underline{a_n},\overline{a_n}\right]$$

Заметим, что для каждого $n$, $$A_{n+1}\subseteq A_n$$

DEF Для каждой последовательности $\langle a_n\rangle$ определите пересечение $$\bigcap_{n\in \Bbb N}A_n=[\zeta,\eta]$$ Это непустое значение, любезно предоставленное теоремой Кантора о пересечении.

Обратите внимание, что $\zeta=\lim\limits_{n\to\infty} \underline{a_n}$ и $\eta=\lim\limits_{n\to\infty} \overline{a_n}$ $\limsup$ и $\liminf$ из $\langle a_n\rangle $.

Докажите

$1.$ Если $\ell$ является предельной точкой $\langle a_n\rangle $, то $\ell \in [\zeta,\eta]$. Это $\mathscr L\subseteq [\zeta,\eta]$.

$2.$ $\eta,\zeta$ — предельные точки $\langle a_n\rangle $, отсюда заключаем, что $\eta,\zeta$ — наименьшая и наибольшая предельные точки $\langle a_n\rangle $. Таким образом, $\zeta=\sup\mathscr L=\max \mathscr L\; ,\; \eta=\inf\mathscr L=\min \mathscr L$.

$3.$ Заметим, что если $\zeta=\eta$, то интервал вырождается в одну точку $p=\zeta=\eta$, а это означает, что тривиальная подпоследовательность $\langle a_n\rangle $ сходится к $p =\зета=\эта$. Обратно, если $\lim\limits_{n\to\infty} a_n=p$, все подпоследовательности сходятся к $p$, поэтому интервал $[\zeta,\eta]$ вырождается в единственную точку $p=\eta =\зета$.

ПРИМЕЧАНИЕ Если последовательность не ограничена сверху (соответственно снизу), то $$\limsup_{n\to\infty}a_n=+\infty\;\;\left( \liminf_{n\to\infty} a_n=-\infty\right)$$

$\endgroup$

2

$\begingroup$

Простой способ понять нижний предел или liminf состоит в том, что для любой последовательности, например -1,1,-1,1,-1,1,-1,1,-1, мы должны найти подпоследовательность последовательности (часть или часть последовательности) и найдите последовательность сходимости чисел с наименьшим значением, числа которой сходятся к числу, которое является наименьшим возможным числом, таким как -1, -1, -1, -1, -1, -1, -1, -1 ,-1,-1,-1-,1,-1,-1,-1,-1,-1,-1,-1 мы видим, что числа равны -1 и сходятся к -1 и так как -1 и 1 — это 2 числовых значения, которые мы могли бы найти -1 — нижний предел, а 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1. …. 1 это числа и сходится к 1

$\endgroup$

1

$\begingroup$

Постараюсь передать интуицию только словами, без математических символов.

• Какое наименьшее число больше или равно бесконечному числу членов последовательности? —> верхний предел

История: Чтобы быть кандидатом на предельный супремум, число должно быть больше или равно бесконечному числу членов последовательности. Для этого нам нужно рассмотреть хвосты последовательности. Почему хвосты? Почему не головы? Поскольку для любого члена все элементы слева от него (головы) имеют конечное число, поскольку последовательность начинается слева и начальная точка известна ([избегая пока двубесконечных последовательностей] последовательность является отображением из набор натуральных чисел, который начинается с 1, поэтому начальная сторона известна. Вы можете назвать первое натуральное число, первые 2 натуральных числа и т. д., но не можете назвать последние 2 натуральных числа), только правая часть бесконечна. Итак, там, где говорят о бесконечном числе членов, вы должны учитывать хвост. Любой хвост последовательности бесконечно длинный. Следовательно, супремум любого хвоста больше или равен бесконечно многим членам последовательности. Таким образом, супремум любого хвоста является кандидатом на предельный супремум. Далее, поскольку последующие хвосты являются подмножествами предыдущих, соответствующие супремумы образуют монотонно убывающую последовательность кандидатов в предельный супремум. Однако инфимум (в данном случае = предел) этой последовательности кандидатов есть наименьшее число, которое уже ограничивает сверху бесконечное множество членов исходной последовательности, что и является целью. Таким образом, мы отбрасываем все более крупные кандидаты, и этот инфимум, как лучший/наиболее экономный кандидат, выбирается в качестве предельного супремума исходной последовательности.

• Какое наибольшее число меньше или равно бесконечному числу элементов последовательности? —> предел инфимума

Теперь вы можете написать историю.

$\endgroup$

1

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Обязательно, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

Исчисление

— опровержение предела наименьшей целочисленной функции

спросил
7 лет, 11 месяцев назад

Изменено
7 лет, 11 месяцев назад

Просмотрено
259 раз

$\begingroup$
9+$ равно $1$.

Каков подход к доказательству того, что предел не существует, используя определение предела?

Я начал с предположения, что предел для $\lfloor x \rfloor$ существует,
$$
|\lэтаж x \rэтаж — L| < \ эпсилон $$ $$ L - \epsilon <\lfloor x \rfloor < L+ \epsilon $$

Я выбрал $\epsilon = 0,5$

$$
L — 0,5<\lпол x \rпол < L+ 0,5 $$

но не знал, как составить противоречие, чтобы доказать это

Помогите?

Спасибо!!

• исчисление
• пределы
• функции
• эпсилон-дельта

$\endgroup$

$\begingroup$

Пусть нашей функцией будет $f(x)$. Предположим, что предел $f(x)$ при $x\to 1$ существует и равен $b$. Тогда для любого $\epsilon\gt 0$ существует $\delta$ такое, что если $0\lt |x-1|\lt \delta$, то $|f(x)-b|\lt \epsilon$ . Воспользуемся этим, чтобы получить противоречие.

Пусть $\epsilon=1/10$, и предположим, что $|f(x)-b|\lt \epsilon$ всякий раз, когда $0\lt |x-1|\lt \delta$.

Существуют такие $x$, что $0\lt |x-1|\lt \delta$ и $f(x)=1$. (Пусть $x=1+\delta/2$.) Таким образом, $|1-b|\lt 1/10$

Аналогично, существуют $x$ такие, что $0\lt |x-1|\lt \ дельта$ и $f(x)=0$. (Просто выберите $x=1-\delta/2$.) Итак, $|0-b|\lt 1/10$.

Но мы пришли к противоречию, так как не существует $b$, которое одновременно находится в пределах $1/10$ от $1$ и в пределах $1/10$ от $0$.

Если хотите, вы можете вместо этого показать, что $b$ не может быть ни $\le 0,5$, ни $\gt 0,5$. Например, это не $\le 0,5$, потому что если бы это было так, то мы бы имели $|1-b|\ge 0,5$, что противоречит тому факту, что $||-b|\lt 1/10$.

$\endgroup$

$\begingroup$

Если под «определением предела» вы подразумеваете определение эпсилон-дельта, то это довольно просто.