Таблица математических символов. Обозначение количество
| ⇒ → ⊃ | Импликация, следование | означает «если верно, то также верно».(→ может использоваться вместо ⇒ или для обозначения функции, см. ниже.)(⊃ может использоваться вместо ⇒, или для обозначения надмножества, см. ниже.). | верно, но неверно (так как также является решением). | |
| «влечёт» или «если…, то» | ||||
| везде | ||||
| ⇔ | Равносильность | означает « верно тогда и только тогда, когда верно». | ||
| «если и только если» или «равносильно» | ||||
| везде | ||||
| ∧ | Конъюнкция | истинно тогда и только тогда, когда и оба истинны. | , если — натуральное число. | |
| «и» | ||||
| Математическая логика | ||||
| ∨ | Дизъюнкция | истинно, когда хотя бы одно из условий и истинно. | , если — натуральное число. | |
| «или» | ||||
| Математическая логика | ||||
| Отрицание | истинно тогда и только тогда, когда ложно . | |||
| «не» | ||||
| Математическая логика | ||||
| ∀ | Квантор всеобщности | обозначает « верно для всех ». | ||
| «Для любых», «Для всех» | ||||
| Математическая логика | ||||
| ∃ | Квантор существования | означает «существует хотя бы один такой, что верно » | (подходит число 5) | |
| «существует» | ||||
| Математическая логика | ||||
| = | Равенство | обозначает « и обозначают одно и то же значение». | 1 + 2 = 6 − 3 | |
| «равно» | ||||
| везде | ||||
| := :⇔ | Определение | означает « по определению равен ». означает « по определению равносильно » | (Гиперболический косинус) (Исключающее или) | |
| «равно/равносильно по определению» | ||||
| везде | ||||
| { , } | Множество элементов | означает множество, элементами которого являются , и . | (множество натуральных чисел) | |
| «Множество…» | ||||
| Теория множеств | ||||
| { | } { : } | Множество элементов, удовлетворяющих условию | означает множество всех таких, что верно . | ||
| «Множество всех… таких, что верно…» | ||||
| Теория множеств | ||||
| ∅ {} | Пустое множество | и означают множество, не содержащее ни одного элемента. | ||
| «Пустое множество» | ||||
| Теория множеств | ||||
∉ | Принадлежность/непринадлежность к множеству | означает « является элементом множества » означает « не является элементом множества » | ||
| «принадлежит», «из»«не принадлежит» | ||||
| Теория множеств | ||||
| ⊆ ⊂ | Подмножество | означает «каждый элемент из также является элементом из ». обычно означает то же, что и . Однако некоторые авторы используют , чтобы показать строгое включение (то есть ). | ||
| «является подмножеством», «включено в» | ||||
| Теория множеств | ||||
| ⊇ ⊃ | Надмножество | означает «каждый элемент из также является элементом из ». обычно означает то же, что и . Однако некоторые авторы используют , чтобы показать строгое включение (то есть ). | ||
| «является надмножеством», «включает в себя» | ||||
| Теория множеств | ||||
| ⊊ | Собственное подмножество | означает и . | ||
| «является собственным подмножеством», «строго включается в» | ||||
| Теория множеств | ||||
| ⊋ | Собственное надмножество | означает и . | ||
| «является собственным надмножеством», «строго включает в себя» | ||||
| Теория множеств | ||||
| ∪ | Объединение | означает множество элементов, принадлежащих или (или обоим сразу). | ||
| «Объединение … и …», «…, объединённое с …» | ||||
| Теория множеств | ||||
| ⋂ | Пересечение | означает множество элементов, принадлежащих и , и . | ||
| «Пересечение … и … », «…, пересечённое с …» | ||||
| Теория множеств | ||||
| Разность множеств | означает множество элементов, принадлежащих , но не принадлежащих . | |||
| «разность … и … », «минус», «… без …» | ||||
| Теория множеств | ||||
| → | Функция | означает функцию с областью определения и областью прибытия (областью значений) . | Функция , определённая как | |
| «из … в», | ||||
| везде | ||||
| ↦ | Отображение | означает, что образом после применения функции будет . | Функцию, определённую как , можно записать так: | |
| «отображается в» | ||||
| везде | ||||
| N или ℕ | Натуральные числа | означает множество или реже (в зависимости от ситуации). | ||
| «Эн» | ||||
| Числа | ||||
| Целые числа | означает множество | |||
| «Зед» | ||||
| Числа | ||||
| Q или ℚ | Рациональные числа | означает | ||
| «Ку» | ||||
| Числа | ||||
| R или ℝ | Вещественные числа, или действительные числа | означает множество всех пределов последовательностей из | ( — комплексное число: ) | |
| «Эр» | ||||
| Числа | ||||
| C или ℂ | Комплексные числа | означает множество | ||
| «Це» | ||||
| Числа | ||||
| <> | Сравнение | обозначает, что строго меньше . означает, что строго больше . | ||
| «меньше чем», «больше чем» | ||||
| Отношение порядка | ||||
| ≤ или ⩽≥ или ⩾ | Сравнение | означает, что меньше или равен . означает, что больше или равен . | ||
| «меньше или равно»; «больше или равно» | ||||
| Отношение порядка | ||||
| ≈ | Приблизительное равенство | с точностью до означает, что 2,718 отличается от не больше чем на . | с точностью до . | |
| «приблизительно равно» | ||||
| Числа | ||||
| √ | Арифметический квадратный корень | означает неотрицательное действительное число, которое в квадрате даёт . | ||
| «Корень квадратный из …» | ||||
| Числа | ||||
| ∞ | Бесконечность | и суть элементы расширенного множества действительных чисел. Эти символы обозначают числа, меньшее/большее всех действительных чисел. | ||
| «Плюс/минус бесконечность» | ||||
| Числа | ||||
| | | | Модуль числа (абсолютное значение), модуль комплексного числа или мощность множества | обозначает абсолютную величину . обозначает мощность множества и равняется, если конечно, числу элементов . | ||
| «Модуль»; «Мощность» | ||||
| Числа и Теория множеств | ||||
| ∑ | Сумма, сумма ряда | означает «сумма , где принимает значения от 1 до », то есть . означает сумму ряда, состоящего из . | ||
| «Сумма … по … от … до …» | ||||
| Арифметика, Математический анализ | ||||
| ∏ | Произведение | означает «произведение для всех от 1 до », то есть | ||
| «Произведение … по … от … до …» | ||||
| Арифметика | ||||
| ! | Факториал | означает «произведение всех натуральных чисел от 1 до включительно, то есть | ||
| « факториал» | ||||
| Комбинаторика | ||||
| ∫ | Интеграл | означает «интеграл от до функции от по переменной ». | ||
| «Интеграл (от … до …) функции … по (или d)…» | ||||
| Математический анализ | ||||
| df/dxf'(x) | Производная | или означает «(первая) производная функции от по переменной ». | ||
| «Производная … по …» | ||||
| Математический анализ | ||||
| Производная -го порядка | или (во втором случае если — фиксированное число, то оно пишется римскими цифрами) означает «-я производная функции от по переменной ». | |||
| «-я производная … по …» | ||||
| Математический анализ |
dic.academic.ru
| A{\displaystyle A} | Площадь (лат. area), векторный потенциал[1], работа (нем. Arbeit), амплитуда (лат. amplitudo), параметр вырождения, работа выхода (нем. Austrittsarbeit), коэффициент Эйнштейна для спонтанного излучения, массовое число |
| a{\displaystyle a} | Ускорение (лат. acceleratio), амплитуда (лат. amplitudo), активность (лат. activitas), коэффициент температуропроводности, вращательная способность, радиус Бора, натуральный показатель поглощения света |
| B{\displaystyle B} | Вектор магнитной индукции[1], барионный заряд (англ. baryon number), удельная газовая постоянная, вириальний коэффициент, функция Бриллюэна (англ. Brillion function), ширина интерференционной полосы (нем. Breite), яркость, постоянная Керра, коэффициент Эйнштейна для вынужденного излучения, коэффициент Эйнштейна для поглощения, вращательная постоянная молекулы |
| b{\displaystyle b} | Вектор магнитной индукции[1], красивый кварк (англ. beauty/bottom quark), постоянная Вина, ширина распада (нем. Breite) |
| C{\displaystyle C} | Электрическая ёмкость (англ. capacitance), теплоёмкость (англ. heatcapacity), постоянная интегрирования (лат. constans), очарование (чарм, шарм; англ. charm), коэффициенты Клебша — Гордана (англ. Clebsch-Gordan coefficients), постоянная Коттона — Мутона (англ. Cotton-Mouton constant), кривизна (лат. curvatura) |
| c{\displaystyle c} | Скорость света (лат. celeritas), скорость звука (лат. celeritas), теплоёмкость (англ. heat capacity), очарованный кварк (англ. charm quark), концентрация (англ. concentration), первая радиационная постоянная, вторая радиационная постоянная |
| D{\displaystyle D} | Вектор электрической индукции[1] (англ. electric displacement field), коэффициент диффузии (англ. diffusion coefficient), оптическая сила (англ. dioptric power), коэффициент прохождения, тензор квадрупольного электрического момента, угловая дисперсия спектрального прибора, линейная дисперсия спектрального прибора, коэффициент прозрачности потенциального барьера, D-мезон (англ. D meson), диаметр (лат. diametros, др.-греч. διάμετρος) |
| d{\displaystyle d} | Расстояние (лат. distantia), диаметр (лат. diametros, др.-греч. διάμετρος), дифференциал (лат. differentia), нижний кварк (англ. down quark), дипольный момент (англ. dipole moment), период дифракционной решётки, толщина (нем. Dicke) |
| E{\displaystyle E} | Энергия (лат. energīa), напряжённость электрического поля[1] (англ. electric field), электродвижущая сила (англ. electromotive force), магнитодвижущая сила, освещенность (фр. éclairement lumineux), излучательная способность тела, модуль Юнга |
| e{\displaystyle e} | Основание натуральных логарифмов (2,71828…), электрон (англ. electron), элементарный электрический заряд (англ. elementaty electric charge), константа электромагнитного взаимодействия |
| F{\displaystyle F} | Сила (лат. fortis), постоянная Фарадея (англ. Faraday constant), свободная энергия Гельмгольца (нем. freie Energie), атомный фактор рассеяния, тензор электромагнитного поля, магнитодвижущая сила, модуль сдвига, фокусное расстояние (англ. focal length) |
| f{\displaystyle f} | Частота (лат. frequentia), функция (лат. functia), летучесть (нем. Flüchtigkeit), сила (лат. fortis), фокусное расстояние (англ. focal length), сила осциллятора, коэффициент трения |
| G{\displaystyle G} | Гравитационная постоянная (англ. gravitational constant), тензор Эйнштейна, свободная энергия Гиббса (англ. Gibbs free energy), метрика пространства-времени, вириал, парциальная мольная величина, поверхностная активность адсорбата, модуль сдвига, полный импульс поля, глюон (англ. gluon), константа Ферми, квант проводимости, электрическая проводимость, вес (нем. Gewichtskraft) |
| g{\displaystyle g} | Ускорение свободного падения (англ. gravitational acceleration), глюон (англ. gluon), фактор Ланде, фактор вырождения, весовая концентрация, гравитон (англ. graviton), метрический тензор |
| H{\displaystyle H} | Напряжённость магнитного поля[1], эквивалентная доза, энтальпия (англ. heat contents или от греческой буквы «эта», H — ενθαλπος[2]), гамильтониан (англ. Hamiltonian), функция Ганкеля (англ. Hankel function), функция Хевисайда (англ. Heaviside step function), бозон Хиггса (англ. Higgs boson), экспозиция, полиномы Эрмита (англ. Hermite polynomials) |
| h{\displaystyle h} | Высота (нем. Höhe), постоянная Планка (нем. Hilfsgröße[3]), спиральность (англ. helicity) |
| I{\displaystyle I} | сила тока (фр. intensité de courant), интенсивность звука (лат. intēnsiō), интенсивность света (лат. intēnsiō), сила излучения, сила света, момент инерции, вектор намагниченности |
| i{\displaystyle i} | Мнимая единица (лат. imaginarius), единичный вектор (координатный орт) |
| J{\displaystyle J} | Плотность тока (также 4-вектор плотности тока), момент импульса, функция Бесселя, момент инерции, полярный момент инерции сечения, вращательное квантовое число, сила света, J/ψ-мезон |
| j{\displaystyle j} | Мнимая единица (в электротехнике и радиоэлектронике), плотность тока (также 4-вектор плотности тока), единичный вектор (координатный орт) |
| K{\displaystyle K} | Каона (англ. kaons), термодинамическая константа равновесия, коэффициент электронной теплопроводности металлов, модуль всестороннего сжатия, механический импульс, постоянная Джозефсона, кинетическая энергия |
| k{\displaystyle k} | Коэффициент (нем. Koeffizient), постоянная Больцмана, теплопроводность, волновое число, единичный вектор (координатный орт) |
| L{\displaystyle L} | Момент импульса, дальность полёта, удельная теплота парообразования и конденсации, индуктивность, функция Лагранжа (англ. Lagrangian), классическая функция Ланжевена (англ. Langevin function), число Лоренца (англ. Lorenz number), уровень звукового давления, полиномы Лагерра (англ. Laguerre polynomials), орбитальное квантовое число, энергетическая яркость, яркость (англ. luminance) |
| l{\displaystyle l} | Длина (англ. length), длина свободного пробега (англ. length), орбитальное квантовое число, радиационная длина |
| M{\displaystyle M} | Момент силы, масса (лат. massa, от др.-греч. μᾶζα, кусок теста), вектор намагниченности (англ. magnetization), крутящий момент, число Маха, взаимная индуктивность, магнитное квантовое число, молярная масса |
| m{\displaystyle m} | Масса, магнитное квантовое число (англ. magnetic quantum number), магнитный момент (англ. magnetic moment), эффективная масса, дефект массы, масса Планка |
| N{\displaystyle N} | Количество (лат. numerus), постоянная Авогадро, число Дебая, полная мощность излучения, увеличение оптического прибора, концентрация, мощность, сила нормальной реакции |
| n{\displaystyle n} | Показатель преломления, количество вещества, нормальный вектор, единичный вектор, нейтрон (англ. neutron), количество (англ. number), основное квантовое число, частота вращения, концентрация, показатель политропы, постоянная Лошмидта |
| O{\displaystyle O} | Начало координат (лат. origo) |
| P{\displaystyle P} | Мощность (лат. potestas), давление (лат. pressūra), полиномы Лежандра, вес (фр. poids), сила тяжести, вероятность (лат. probabilitas), поляризуемость, вероятность перехода, импульс (также 4-импульс, обобщённый импульс; лат. petere) |
| p{\displaystyle p} | Импульс (также 4-импульс, обобщённый импульс; лат. petere), протон (англ. proton), дипольный момент, волновой параметр, давление, число полюсов, плотность. |
| Q{\displaystyle Q} | Электрический заряд (англ. quantity of electricity), количество теплоты (англ. quantity of heat), объёмный расход, обобщённая сила, хладопроизводительность, энергия излучения, световая энергия, добротность (англ. quality factor), нулевой инвариант Аббе, квадрупольный электрический момент (англ. quadrupole moment), энергия ядерной реакции |
| q{\displaystyle q} | Электрический заряд, обобщённая координата, количество теплоты (англ. quantity of heat), эффективный заряд, добротность |
| R{\displaystyle R} | Электрическое сопротивление (англ. resistance), универсальная газовая постоянная, постоянная Ридберга (англ. R ydberg constant), постоянная фон Клитцинга, коэффициент отражения, сопротивление излучения (англ. resistance), разрешение (англ. resolution), светимость, пробег частицы, расстояние |
| r{\displaystyle r} | Радиус (лат. radius), радиус-вектор, радиальная полярная координата, удельная теплота фазового перехода, удельная рефракция (лат. rēfractiō), расстояние |
| S{\displaystyle S} | Площадь поверхности (англ. surface area), энтропия[4], действие, спин (англ. spin), спиновое квантовое число (англ. spin quantum number), странность (англ. strangeness), главная функция Гамильтона, матрица рассеяния (англ. scattering matrix), оператор эволюции, вектор Пойнтинга |
| s{\displaystyle s} | Перемещение (итал. spostamento), странный кварк (англ. strange quark), путь, пространственно-временной интервал (англ. spacetime interval), оптическая длина пути |
| T{\displaystyle T} | Температура (лат. temperātūra), период (лат. tempus), кинетическая энергия, критическая температура, терм, период полураспада, критическая энергия, изоспин |
| t{\displaystyle t} | Время (лат. tempus), истинный кварк (англ. true quark), правдивость (англ. truth), планковское время |
| U{\displaystyle U} | Внутренняя энергия, потенциальная энергия, вектор Умова, потенциал Леннард-Джонса, потенциал Морзе, 4-скорость, электрическое напряжение |
| u{\displaystyle u} | Верхний кварк (англ. up quark), скорость, подвижность, удельная внутренняя энергия, групповая скорость |
| V{\displaystyle V} | Объём (фр. volume), электрическое напряжение (англ. voltage), потенциальная энергия, видность полосы интерференции, постоянная Верде (англ. Verdet constant) |
| v{\displaystyle v} | Скорость (лат. vēlōcitās), фазовая скорость, удельный объём |
| W{\displaystyle W} | Механическая работа (англ. work), работа выхода, W-бозон, энергия, энергия связи атомного ядра, мощность |
| w{\displaystyle w} | Скорость, плотность энергии, коэффициент внутренней конверсии, ускорение |
| X{\displaystyle X} | Реактивное сопротивление, продольное увеличение, X-бозон |
| x{\displaystyle x} | Переменная, перемещение, абсцисса (декартова координата), молярная концентрация, постоянная ангармоничности, расстояние |
| Y{\displaystyle Y} | Гиперзаряд, силовая функция, линейное увеличение, сферические функции, Y-бозон |
| y{\displaystyle y} | ордината (декартова координата) |
| Z{\displaystyle Z} | Импеданс, Z-бозон, атомный номер или зарядовое число ядра (нем. Ordnungszahl), статистическая сумма (нем. Zustandssumme), вектор Герца, валентность, полное электрическое сопротивление (импеданс), угловое увеличение, волновое сопротивление вакуума |
| z{\displaystyle z} | аппликата (декартова координата) |
ru-wiki.org
Величины | |
Наименование | Обозначение |
Механические величины | |
| Вес | G, P, W |
| Время | t |
| Высота | h |
| Давление | p |
| Диаметр | d |
| Длина | l |
| Длина пути | s |
| Импульс (количество движения) | p |
| Количество вещества | ν, n |
| Коэффицент жесткости (жесткость) | Ʀ |
| Коэффицент запаса прочности | Ʀ, n |
| Коэффицент полезного действия | η |
| Коэффицент трения качения | Ʀ |
| Коэффицент трения скольжения | μ, f |
| Масса | m |
| Масса атома | ma |
| Масса электрона | me |
| Механическое напряжение | σ |
| Модуль упругости (модуль Юнга) | E |
| Момент силы | M |
| Мощность | P, N |
| Объем, вместимость | V, ϑ |
| Период колебания | T |
| Плотность | ϱ |
| Площадь | A, S |
| Поверхностное натяжение | σ, γ |
| Постоянная гравитационная | G |
| Предел прочности | σпч |
| Работа | W, A, L |
| Радиус | r, R |
| Сила, сила тяжести | F, Q, R |
| Скорость линейная | ϑ |
| Скорость угловая | ώ |
| Толщина | d, δ |
| Ускорение линейное | a |
| Ускорение свободного падения | g |
| Частота | ν, f |
| Частота вращения | n |
| Ширина | b |
| Энергия | E, W |
| Энергия кинетитеская | EƦ |
| Энергия потенциальная | Ep |
Акустические величины | |
| Длина волны | λ |
| Звуковая мощность | P |
| Звуковая энергия | W |
| Интенсивность звука | I |
| Скорость звука | c |
| Частота | ν, f |
Тепловые величины и величины молекулярной физики | |
| Абсолютная влажность | a |
| Газовая постоянная (молярная) | R |
| Количество теплоты | Q |
| Коэффицент полезного действия | η |
| Относительная влажность | ϕ |
| Относительная молекулярная масса | Mr |
| Постоянная (число) Авогадро | NA |
| Постоянная Больцмана | Ʀ |
| Постоянная (число) Лошмидта | NL |
| Температура Кюри | TC |
| Температура па шкале Цельсия | t, ϴ |
| Температура термодинамическая (абсолютная температура) | T |
| Температурный коэффицент линейного расширения | a, ai |
| Температурный коффицент объемного расширения | β, av |
| Удельная теплоемкость | c |
| Удельная теплота парообразования | r |
| Удельная теплота плавления | λ |
| Удельная теплота сгорания топлива (сокращенно: теплота сгорания топлива) | q |
| Число молекул | N |
| Энергия внутренняя | U |
Электрические и магнитные величины | |
| Диэлектрическая проницаемость вакуума (электрическая постоянная) | Ԑo |
| Индуктивность | L |
| Коэффицент самоиндукции | L |
| Коэффицент трансформации | K |
| Магнитная индукция | B |
| Магнитная проницаемость вакуума (магнитная постоянная) | μo |
| Магнитный поток | Ф |
| Мощность электрической цепи | P |
| Напряженность магнитного поля | H |
| Напряженность электрического поля | E |
| Объемная плотность электрического заряда | ϱ |
| Относительная диэлектрическая проницаемость | Ԑr |
| Относительная магнитная проницаемость | μr |
| Плотность эенгии магнитного поля удельная | ωm |
| Плотность энергии электрического поля удельная | ωэ |
| Плотность заряда поверхностная | σ |
| Плотность электрического тока | J |
| Постоянная (число) Фарадея | F |
| Проницаемость диэлектрическая | ԑ |
| Работа выхода электрона | ϕ |
| Разность потенциалов | U |
| Сила тока | I |
| Температурный коэффицент электрического сопротивления | a |
| Удельная электрическая проводимость | γ |
| Удельное электрическое сопротивление | ϱ |
| Частота электрического тока | f, ν |
| Число виток обмотки | N, ω |
| Электрическая емкость | C |
| Электрическая индукция | D |
| Электрическая проводимость | G |
| Электрический момент диполя молекулы | p |
| Электрический заряд (количество электричества) | Q, q |
| Электрический потенциал | V, ω |
| Электрическое напряжение | U |
| Электрическое сопротивление | R, r |
| Электродвижущая сила | E, Ԑ |
| Электрохимический эквивалент | Ʀ |
| Энергия магнитного поля | Wm |
| Энергия электрического поля | Wэ |
| Энергия Электромагнитная | W |
Оптические величины | |
| Длина волны | λ |
| Освещенность | E |
| Период колебания | T |
| Плотность потока излучения | Ф |
| Показатель (коэффицент) преломления | n |
| Световой поток | Ф |
| Светасила объектива | f |
| Сила света | I |
| Скорость света | c |
| Увеличение линейное | β |
| Увеличение окуляра, микроскопа, лупы | Ѓ |
| Угол отражения луча | έ |
| Угол падения луча | ԑ |
| Фокусное расстояние | F |
| Частота колебаний | ν, f |
| Энергия излучения | Q, W |
| Энергия световая | Q |
Величины атомной физики | |
| Атомная масса относительная | Ar |
| Время полураспада | T1/2 |
| Дефект массы | Δ |
| Заряд электрона | e |
| Масса атома | ma |
| Масса нейтрона | mn |
| Масса протона | mp |
| Масса электрона | me |
| Постоянная Планка | h, ħ |
| Радиус электрона | re |
Величины ионизирующих излучений | |
| Поглощеная доза излучения (доза излучения) | D |
| Мощность поглощенной дозы излучения | Ď |
| Активность нуклида в радиоактивном источнике | A |
www.kilomol.ru
Математические знаки и символы: список, таблица, история возникновения
Когда люди долгое время взаимодействуют в рамках определенной сферы деятельности, они начинают искать способ оптимизировать процесс коммуникации. Система математических знаков и символов представляет собой искусственный язык, который был разработан, чтобы уменьшить объем графически передаваемой информации и при этом полностью сохранить заложенный в сообщение смысл.
Любой язык требует изучения, и язык математики в этом плане – не исключение. Чтобы понимать значение формул, уравнений и графиков, требуется заранее владеть определенной информацией, разбираться в терминах, системе обозначений и т. д. При отсутствии такого знания текст будет восприниматься как написанный на незнакомом иностранном языке.
В соответствии с запросами общества графические символы для более простых математических операций (например, обозначение сложения и вычитания) были выработаны раньше, чем для сложных понятий наподобие интеграла или дифференциала. Чем сложнее понятие, тем более сложным знаком оно обычно обозначается.
Модели образования графических обозначений
На ранних этапах развития цивилизации люди связывали простейшие математические операции с привычными для них понятиями на основе ассоциаций. Например, в Древнем Египте сложение и вычитание обозначались рисунком идущих ног: направленные по направлению чтения строки они обозначали «плюс», а в обратную сторону – «минус».
Цифры, пожалуй, во всех культурах изначально обозначались соответствующим количеством черточек. Позже для записи стали использоваться условные обозначения - это экономило время, а также место на материальных носителях. Часто в качестве символов использовались буквы: такая стратегия получила распространение в греческом, латинском и многих других языках мира.
История возникновения математических символов и знаков знает два наиболее продуктивных способа образования графических элементов.
Преобразование словесного представления
Изначально любое математическое понятие выражается некоторым словом или словосочетанием и не имеет собственного графического представления (помимо лексического). Однако выполнение расчетов и написание формул словами – процедура длительная и занимающая неоправданно много места на материальном носителе.
Распространенный способ создания математических символов – трансформация лексического представления понятия в графический элемент. Иначе говоря, слово, обозначающее понятие, с течением времени сокращается или преобразуется каким-либо другим способом.
Например, основной гипотезой происхождения знака «плюс» является его сокращение от латинского et, аналогом которого в русском языке является союз «и». Постепенно в скорописи первая буква перестала писаться, а t сократилась до креста.
Другой пример – знак «икс», обозначающий неизвестное, который изначально представлял собой сокращение от арабского слова «нечто». Сходным образом произошли знаки для обозначения квадратного корня, процента, интеграла, логарифма и др. В таблице математических символов и знаков можно встретить более десятка графических элементов, появившихся таким образом.
Назначение произвольного символа
Второй распространенный вариант образования математических знаков и символов – назначение символа произвольным образом. В этом случае слово и графическое обозначение между собой не связаны - знак обычно утверждается в результате рекомендации одного из членов научного сообщества.
Например, знаки умножения, деления, равенства были предложены математиками Уильямом Отредом, Иоганном Раном и Робертом Рекордом. В некоторых случаях несколько математических знаков могли быть введены в науку одним ученым. В частности, Готфрид Вильгельм Лейбниц предложил целый ряд символов, в том числе интеграла, дифференциала, производной.
Простейшие операции
Такие знаки, как «плюс» и «минус», а также символы, обозначающие умножение и деление, знает каждый школьник, несмотря на то, что для последних двух упомянутых операций существует несколько возможных графических знаков.
Можно с уверенностью говорить, что складывать и вычитать люди умели ещё за много тысячелетий до нашей эры, а вот стандартизованные математические знаки и символы, обозначающие данные действия и известные нам сегодня, появились лишь к XIV-XV столетию.
Впрочем, несмотря на установление определенной договоренности в научном сообществе, умножение и в наше время может изображаться тремя различными знаками (диагональный крестик, точка, звёздочка), а деление – двумя (горизонтальная черта с точками сверху и снизу или наклонная черта).
Латинские буквы
На протяжении многих столетий научное сообщество использовало для обмена информацией исключительно латынь, и многие математические термины и знаки обнаруживают свои истоки именно в этом языке. В некоторых случаях графические элементы стали результатом сокращения слов, реже – их намеренного или случайного преобразования (например, вследствие описки).
Обозначение процента («%»), вероятнее всего, происходит от ошибочного написания сокращения cto (cento, т. е. «сотая доля»). Сходным образом произошёл знак «плюс», история которого описана выше.
Гораздо большее количество символов было образовано путём намеренного сокращения слова, хотя это не всегда очевидно. Далеко не каждый человек узнает в знаке квадратного корня букву R, т. е. первый знак в слове Radix («корень»). Символ интеграла также представляет собой первую букву слова Summa, однако интуитивно она похожа на прописную f без горизонтальной черты. К слову, в первой публикации издатели совершили именно такую ошибку, напечатав f вместо данного символа.
Греческие буквы
В качестве графических обозначений для различных понятий используются не только латинские, но и греческие буквы. В таблице математических символов можно найти целый ряд примеров такого наименования.
Число Пи, представляющее собой отношение длины окружности к её диаметру, произошло от первой буквы греческого слова, обозначающего окружность. Существует ещё несколько менее известных иррациональных чисел, обозначаемых буквами греческого алфавита.
Крайне распространенным знаком в математике является «дельта», отражающая величину изменения значения переменных. Ещё одним употребительным знаком является «сигма», выполняющая функцию знака суммы.
Более того, практически все греческие буквы так или иначе используются в математике. Однако данные математические знаки и символы и их значение знают только люди, занимающиеся наукой профессионально. В быту и повседневной жизни эти знания человеку не требуются.
Знаки логики
Как ни странно, многие интуитивно понятные символы были придуманы совсем недавно.
В частности, горизонтальная стрелка, заменяющая слово «следовательно», была предложена лишь в 1922 года Давидом Гильбертом. Кванторы существования и всеобщности, т. е. знаки, читающиеся как: «существует…» и «для любого…», были введены в 1897 и 1935 году соответственно.
Символы из области теории множеств были придуманы в 1888-1889 гг. А перечеркнутый круг, который сегодня известен любому учащемуся средней школы как знак пустого множества, появился в 1939 году.
Таким образом, знаки для столь непростых понятий, как интеграл или логарифм, были придуманы на столетия раньше, чем некоторые интуитивно понятные символы, легко воспринимаемые и усваиваемые даже без предварительной подготовки.
Математические символы на английском
Ввиду того, что значительная часть понятий была описана в научных трудах на латыни, ряд названий математических знаков и символов на английском и русском языке одинаковы. Например: Plus («плюс»), Integral («интеграл»), Delta function («дельта-функция»), Perpendicular («перпендикулярный»), Parallel («параллельный»), Null («нуль»).
Часть понятий в двух языках называются различным образом: так, деление – это Division, умножение – Multiplication. В редких случаях английское название для математического знака получает некоторое распространение в русском языке: например, косая черта в последние годы нередко именуется «слешем» (англ. Slash).
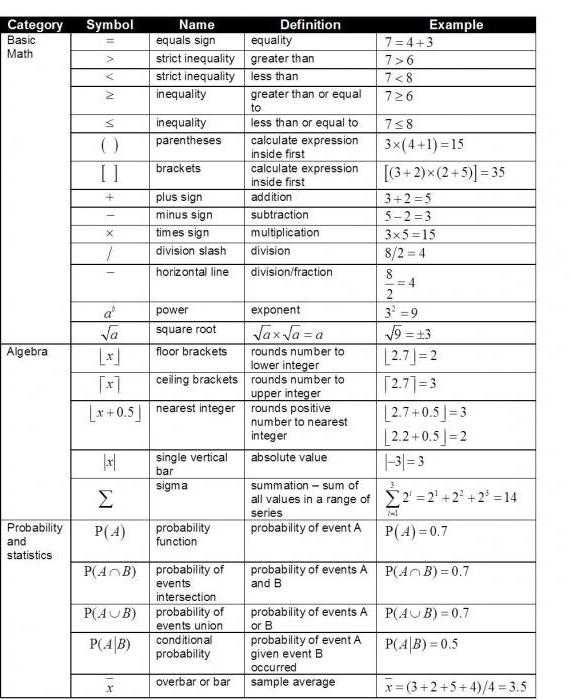
Таблица символов
Самый простой и удобный способ ознакомиться с перечнем математических знаков – посмотреть специальную таблицу, в которой содержатся знаки операций, символы математической логики, теории множеств, геометрии, комбинаторики, математического анализа, линейной алгебры. В данной таблице представлены основные математические знаки на английском языке.
Математические знаки в текстовом редакторе
При выполнении различного рода работ зачастую требуется использовать формулы, где употребляются знаки, отсутствующие на клавиатуре компьютера.
Как и графические элементы из практически любой области знаний, математические знаки и символы в «Ворде» можно найти во вкладке «Вставка». В версиях программы 2003 или 2007 года существует опция «Вставка символа»: при нажатии на кнопку в правой части панели пользователь увидит таблицу, в которой представлены все необходимые математические знаки, греческие строчные и прописные буквы, различные виды скобок и многое другое.
В версиях программы, вышедших после 2010 года, разработана более удобная опция. При нажатии на кнопку «Формула» происходит переход в конструктор формул, где предусмотрено использование дробей, занесения данных под корень, смена регистра (для обозначения степеней или порядковых номеров переменных). Здесь же могут быть найдены все знаки из таблицы, представленной выше.
Стоит ли учить математические символы
Система математических обозначений представляет собой искусственный язык, который лишь упрощает процесс записи, но не может принести понимание предмета стороннему наблюдателю. Таким образом, запоминание знаков без изучения терминов, правил, логических связей между понятиями не приведет к овладению данной областью знаний.
Человеческий мозг легко усваивает знаки, буквы и сокращения – математические обозначения запоминаются сами при изучении предмета. Понимание смысла каждого конкретного действия создает настолько прочные ассоциативные связи, что знаки, обозначающие термины, а зачастую и формулы, связанные с ними, остаются в памяти на многие годы и даже десятилетия.
В заключение
Поскольку любой язык, в том числе искусственный, является открытым к изменениям и дополнениям, число математических знаков и символов непременно будет расти с течением времени. Не исключено, что какие-то элементы будут заменены или скорректированы, а другие – стандартизованы в единственно возможном виде, что актуально, например, для знаков умножения или деления.
Умение пользоваться математическими символами на уровне полного школьного курса является в современном мире практически необходимым. В условиях бурного развития информационных технологий и науки, повсеместной алгоритмизации и автоматизации владение математическим аппаратом следует воспринимать как данность, а освоение математических символов – как неотъемлемую его часть.
Поскольку расчеты используются и в гуманитарной сфере, и в экономике, и в естественных науках, и, разумеется, в области техники и высоких технологий, понимание математических понятий и знание символов станет полезным для любого специалиста.
fb.ru
Величины |
|
Наименование |
Обозначение |
Механические величины |
|
| Вес | G, P, W |
| Время | t |
| Высота | h |
| Давление | p |
| Диаметр | d |
| Длина | l |
| Длина пути | s |
| Импульс (количество движения) | p |
| Количество вещества | ν, n |
| Коэффициент жесткости (жесткость) | Ʀ |
| Коэффициент запаса прочности | Ʀ, n |
| Коэффициент полезного действия | η |
| Коэффициент трения качения | Ʀ |
| Коэффициент трения скольжения | μ, f |
| Масса | m |
| Масса атома | ma |
| Масса электрона | me |
| Механическое напряжение | σ |
| Модуль упругости (модуль Юнга) | E |
| Момент силы | M |
| Мощность | P, N |
| Объем, вместимость | V, ϑ |
| Период колебания | T |
| Плотность | ϱ |
| Площадь | A, S |
| Поверхностное натяжение | σ, γ |
| Постоянная гравитационная | G |
| Предел прочности | σпч |
| Работа | W, A, L |
| Радиус | r, R |
| Сила, сила тяжести | F, Q, R |
| Скорость линейная | ϑ |
| Скорость угловая | ώ |
| Толщина | d, δ |
| Ускорение линейное | a |
| Ускорение свободного падения | g |
| Частота | ν, f |
| Частота вращения | n |
| Ширина | b |
| Энергия | E, W |
| Энергия кинетическая | EƦ |
| Энергия потенциальная | Ep |
Акустические величины |
|
| Длина волны | λ |
| Звуковая мощность | P |
| Звуковая энергия | W |
| Интенсивность звука | I |
| Скорость звука | c |
| Частота | ν, f |
Тепловые величины и величины молекулярной физики |
|
| Абсолютная влажность | a |
| Газовая постоянная (молярная) | R |
| Количество теплоты | Q |
| Коэффицент полезного действия | η |
| Относительная влажность | ϕ |
| Относительная молекулярная масса | Mr |
| Постоянная (число) Авогадро | NA |
| Постоянная Больцмана | Ʀ |
| Постоянная (число) Лошмидта | NL |
| Температура Кюри | TC |
| Температура па шкале Цельсия | t, ϴ |
| Температура термодинамическая (абсолютная температура) | T |
| Температурный коэффицент линейного расширения | a, ai |
| Температурный коффицент объемного расширения | β, av |
| Удельная теплоемкость | c |
| Удельная теплота парообразования | r |
| Удельная теплота плавления | λ |
| Удельная теплота сгорания топлива (сокращенно: теплота сгорания топлива) | q |
| Число молекул | N |
| Энергия внутренняя | U |
Электрические и магнитные величины |
|
| Диэлектрическая проницаемость вакуума (электрическая постоянная) | Ԑo |
| Индуктивность | L |
| Коэффицент самоиндукции | L |
| Коэффицент трансформации | K |
| Магнитная индукция | B |
| Магнитная проницаемость вакуума (магнитная постоянная) | μo |
| Магнитный поток | Ф |
| Мощность электрической цепи | P |
| Напряженность магнитного поля | H |
| Напряженность электрического поля | E |
| Объемная плотность электрического заряда | ϱ |
| Относительная диэлектрическая проницаемость | Ԑr |
| Относительная магнитная проницаемость | μr |
| Плотность энергии магнитного поля удельная | ωm |
| Плотность энергии электрического поля удельная | ωэ |
| Плотность заряда поверхностная | σ |
| Плотность электрического тока | J |
| Постоянная (число) Фарадея | F |
| Проницаемость диэлектрическая | ԑ |
| Работа выхода электрона | ϕ |
| Разность потенциалов | U |
| Сила тока | I |
| Температурный коэффицент электрического сопротивления | a |
| Удельная электрическая проводимость | γ |
| Удельное электрическое сопротивление | ϱ |
| Частота электрического тока | f, ν |
| Число виток обмотки | N, ω |
| Электрическая емкость | C |
| Электрическая индукция | D |
| Электрическая проводимость | G |
| Электрический момент диполя молекулы | p |
| Электрический заряд (количество электричества) | Q, q |
| Электрический потенциал | V, ω |
| Электрическое напряжение | U |
| Электрическое сопротивление | R, r |
| Электродвижущая сила | E, Ԑ |
| Электрохимический эквивалент | Ʀ |
| Энергия магнитного поля | Wm |
| Энергия электрического поля | Wэ |
| Энергия Электромагнитная | W |
Оптические величины |
|
| Длина волны | λ |
| Освещенность | E |
| Период колебания | T |
| Плотность потока излучения | Ф |
| Показатель (коэффицент) преломления | n |
| Световой поток | Ф |
| Света сила объектива | f |
| Сила света | I |
| Скорость света | c |
| Увеличение линейное | β |
| Увеличение окуляра, микроскопа, лупы | Ѓ |
| Угол отражения луча | έ |
| Угол падения луча | ԑ |
| Фокусное расстояние | F |
| Частота колебаний | ν, f |
| Энергия излучения | Q, W |
| Энергия световая | Q |
Величины атомной физики |
|
| Атомная масса относительная | Ar |
| Время полураспада | T1/2 |
| Дефект массы | Δ |
| Заряд электрона | e |
| Масса атома | ma |
| Масса нейтрона | mn |
| Масса протона | mp |
| Масса электрона | me |
| Постоянная Планка | h, ħ |
| Радиус электрона | re |
Величины ионизирующих излучений |
|
| Поглощеная доза излучения (доза излучения) | D |
| Мощность поглощенной дозы излучения | Ď |
| Активность нуклида в радиоактивном источнике | A |
nanomil.ru
Обозначения чисел
Каждое число занимает очень важное место в жизни и что-обозначает. Так, например сейчас вычислительная система используется во всех сферах жизнедеятельности. Её широко используют в составлении гороскопов, в которые верят многие люди, а в древнем мире люди верили в магическую силу чисел и относились к ним очень осторожно, мы считаем, что осторожность нужно проявлять и в наше время, ведь кто знает, что будет, может на числах держится весь мир. Давайте посмотрим чтоже всё таки обозначают они на самом деле.
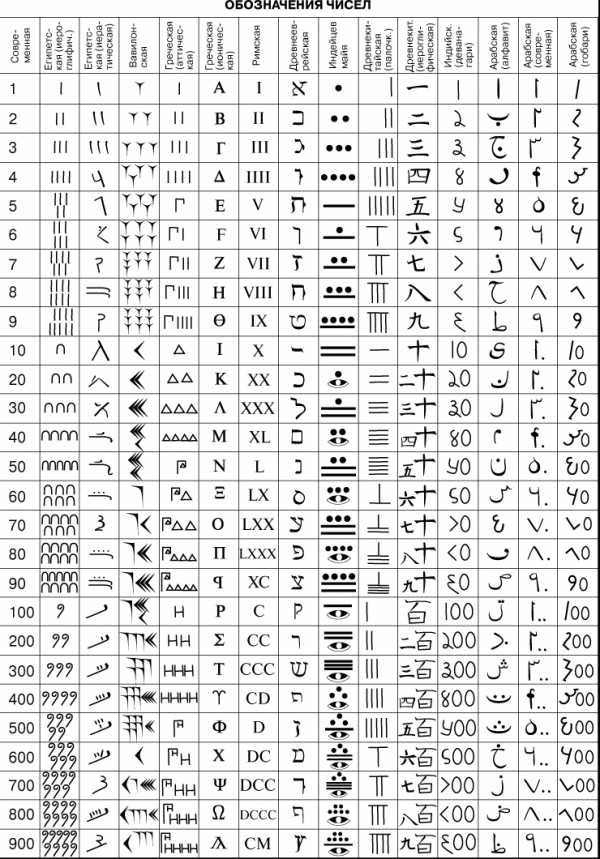
ОБОЗНАЧЕНИЯ ЧИСЕЛ
Древний Египет. Расшифровка системы счисления, созданной в Египте во времена первой династии (ок. 2850 до н.э.), была существенно облегчена тем, что иероглифические надписи древних египтян были аккуратно вырезаны на каменных монументах. Из этих надписей нам известно, что древние египтяне использовали только десятичную систему счисления. Единицу обозначали одной вертикальной чертой, а для обозначения чисел, меньших 10, нужно было поставить соответствующее число вертикальных штрихов. (См. сводную таблицу обозначений чисел.) Чтобы записанные таким образом числа было легко узнавать, вертикальные штрихи иногда объединялись в группы из трех или четырех черт. Для обозначения числа 10, основания системы, египтяне вместо десяти вертикальных черт ввели новый коллективный символ, напоминающий по своим очертаниям подкову или крокетную дужку. Множество из десяти подковообразных символов, т.е. число 100, они заменили другим новым символом, напоминающим силки; десять силков, т.е. число 1000, египтяне обозначили стилизованным изображением лотоса. Продолжая в том же духе, египтяне обозначили десять лотосов согнутым пальцем, десять согнутых пальцев – волнистой линией и десять волнистых линий – фигуркой удивленного человека. В итоге древние египтяне могли представлять числа до миллиона. Так, например, с помощью коллективных символов и повторений уже введенных символов число 6789 в иероглифических обозначениях можно было бы записать как.
Самые древние из дошедших до нас математических записей высечены на камне, но наиболее важные свидетельства древнеегипетской математической деятельности запечатлены на гораздо более хрупком и недолговечном материале – папирусе. Два таких документа – папирус Ринда, или египетского писца Ахмеса (ок. 1650 до н.э.) и московский папирус, или папирус Голенищева (ок. 1850 до н.э.) – служат для нас основными источниками сведений о древнеегипетских арифметике и геометрии. В этих папирусах более древнее иероглифическое письмо уступило место скорописному иератическому письму, и это изменение сопровождалось использованием нового принципа обозначения чисел. Группа одинаковых символов заменялись более простой по начертанию пометой или знаком, например, девять записывалось как 
вместо , а семьсот как 
вместо . В этой записи число 6789 имело вид , причем знаки более высокого порядка располагались справа, а не слева. Иероглифическая запись чисел использовалась преимущественно в официальных документах и текстах. Еще позднее иератическая система обозначения чисел уступила место демотическим системам записи.
Введение египтянами цифровых обозначений ознаменовало один из важных этапов в развитии систем счисления, так как дало возможность существенно сократить записи. Однако их операции с дробями продолжали оставаться на примитивном уровне, так как они знали лишь аликвотные дроби (т.е. дроби с числителем 1) и каждую дробь записывали в виде суммы аликвотных дробей, например, дробь 2/43 они записали бы так: 1/42 + 1/86 + 1/129 + 1/301. В этих системах счисления над символом, обозначающим знаменатель, ставился специальный знак. В искусстве оперирования дробями египтяне значительно уступали жителямМесопотамии. .
Вавилон. Письменность шумеров является, по-видимому, столь же древней, как и письменность египтян. Развитие способов представления чисел в Месопотамской долине вначале шло так же, как и в долине Нила, но затем жители Междуречья ввели совершенно новый принцип. Вавилоняне делали записи острой палочкой на мягких глиняных табличках, которые затем обжигались на солнце или в печи. Эти записи оказались исключительно долговечными, а потому, в отличие от египетских папирусов, дошедших до нас в весьма малом числе экземпляров, в музеях мира хранятся десятки тысяч клинописных табличек. Однако жесткость материала, на котором жители Месопотамии делали записи, оказала глубокое влияние на развитие числовых обозначений. Через некоторое время после того, как Аккад завоевал шумеров, система счисления в Месопотамии стала шестидесятиричной, хотя сохранилось также и основание 10. Казавшееся правдоподобным предположение относительно того, почему выбор пал на число 60 как на основу вавилонской системы счисления, и утверждавшее, будто это связано с тем, что продолжительность земного года считалась равной 360 дням, не получило подтверждения. Ныне принято считать, что шестидесятиричная система была выбрана из метрологических соображений: число 60 имеет много делителей.
Для малых чисел вавилонская система счисления в основных чертах напоминала египетскую. Одна вертикальная клинообразная черта (в раннешумерских табличках – небольшой полукруг) означала единицу; повторенный нужное число раз, этот знак служил для записи чисел меньше десяти; для обозначения числа 10 вавилоняне, как и египтяне, ввели новый коллективный символ – более широкий клиновидный знак с острием, направленным влево, напоминающий по форме угловую скобку, (в раннешумерских текстах – небольшой кружок).
Повторенный соответствующее число раз, этот знак служил для обозначения чисел 20, 30, 40 и 50. Принцип повторного использования знаков позволял, например, записать число 59 в виде , т.е. 5?10 + 9.
Но для записи чисел больше 59 древние вавилоняне впервые использовали новый принцип – одно из самых выдающихся достижений в развитии систем обозначений чисел – принцип позиционности, т.е. зависимости значения символа от его местоположения в записи числа. Вавилоняне заметили, что в качестве коллективных символов более высокого порядка можно применять уже ранее использованные символы, если они будут занимать в записи числа новое положение левее предыдущих символов. Так, один клиновидный знак мог использоваться для обозначения и 1, и 60, и 602, и 603, в зависимости от занимаемого им в записи числа положения, подобно тому, как единица в наших обозначениях используется в записях и 10, и 102, и 103, и в числе 1111. При обозначении чисел больше 60 знаки, выступающие в новом качестве, отличались от старых тем, что символы разбивались на «места», или «позиции», и единицы более высокого порядка располагались слева. При таком способе записи для обозначения сколь угодно больших чисел уже не нужно было других символов, кроме уже известных. Например, число 6789 можно было записать так: , т.е. 1?(60)2 + 53?(60) + 9. В Древнем Вавилоне, ок. 1650 до н.э., система счисления оставалась псевдопозиционной или лишь относительно позиционной, поскольку не существовало эквивалента современной десятичной запятой, равно как и символа для обозначения отсутствующей позиции. Обозначал ли символ число 1?(60)2 + 1 или 1?(60)2 + 1?(60), приходилось догадываться из контекста. Однако в период правления селевкидов, ок. 300 до н.э., эта неоднозначность была устранена введением специального символа в виде двух небольших клиньев, помещаемого на пустующее место, т.е. обозначающего пустую позицию в записи числа. Таким образом, из системы счисления была устранена отмеченная выше неоднозначность. Например, символ означал число 3601, т.е. 1?(60)2 + 0?(60) + 1. В то же время не было найдено ни одной таблички с записью, в которой символ нуля находился бы в конце числа. Именно поэтому вавилонскую систему мы считаем лишь относительно позиционной, ибо самый правый знак мог означать либо единицы, либо кратные какой-нибудь степени числа 60. Тем не менее изобретение вавилонянами позиционной системы счисления с нулем представляло собой огромное достижение, по своему революционному значению для математики сопоставимое разве лишь с более поздней гипотезой Коперника в астрономии.
Символы для обозначения чисел на вавилонских глиняных табличках не столь точны, как символы для обозначения чисел на древнеегипетских папирусах, несмотря на то, что вавилоняне использовали позиционный принцип. В исключительных случаях вавилоняне применяли сокращенные формы записи, иногда – с новыми символами для обозначения чисел 100 и 1000, или использовали принципы умножения или вычитания. Однако превосходство разработанной в Месопотамии системы счисления отчетливо видно в обозначении дробей. Здесь не требовалось вводить новые символы. Как и в нашей собственной десятичной позиционной системе, в древневавилонской системе подразумевалось, что на первом месте справа от единиц стоят величины, кратные 1/60, на втором месте – величины кратные 1/602 и т.д. Привычное нам деление часа и углового или дугового градуса на 60 минут, а одной минуты – на 60 секунд берет начало от вавилонской системы счисления.
Древняя Греция. В Древней Греции имели хождение две основных системы счисления – аттическая (или геродианова) и ионическая (она же александрийская или алфавитная). Аттическая система счисления использовалась греками, по-видимому, уже к 5 в. до н.э. По существу это была десятичная система (хотя в ней также было выделено и число пять), а аттические обозначения чисел использовали повторы коллективных символов. Черта, обозначавшая единицу, повторенная нужное число раз, означала числа до четырех. После четырех черт греки вместо пяти черт ввели новый символ Г, первую букву слова «пента» (пять) (буква Г употреблялась для обозначения звука «п», а не «г»). Дойдя до десяти, они ввели еще один новый символ D, первую букву слова «дека» (десять). Так как система была десятичной, грекам потребовались новые символы для каждой новой степени числа 10: символ H означал 100 (гекатон), X – 1000 (хилиои), символ M – 10000 (мириои или мириада). Используя число 5 как промежуточное подоснование системы счисления, греки на основе принципа умножения комбинировали пятерку с символами степеней числа 10. Так, число 50 они обозначали символом , 500 – символом , 5000 – символом , 50000 – символом . Еще большие числа обычно описывались словами. Число 6789 в аттической системе записывалось в виде .
Вторая принятая в Древней Греции ионическая система счисления – алфавитная – получила широкое распространение в начале Александрийской эпохи, хотя возникнуть она могла несколькими столетиями раньше, по всей видимости, уже у пифагорейцев. Эта более тонкая система счисления была чисто десятичной, и числа в ней обозначались примерно так же, как в древнеегипетской иератической системе. Используя двадцать четыре буквы греческого алфавита и, кроме того, еще три архаических знака, ионическая система сопоставила девять букв первым девяти числам; другие девять букв – первым девяти целым кратным числа десять; и последние девять символов – первым девяти целым кратным числа 100. Для обозначения первых девяти целых кратных числа 1000 греки частично воспользовались древневавилонским принципом позиционности, снова использовав первые девять букв греческого алфавита, снабдив их штрихами слева. Например, число 6789 в ионической системе записывалось как FYPQ. Чтобы отличить числа от слов, греки над соответствующей буквой ставили горизонтальную черту. Первоначально числа обозначались прописными буквами, но позднее сменились на строчные.
Ионическая система первоначально не сильно потеснила уже установившуюся аттическую или акрофоническую (по начальным буквам слов, означавших числительные) системы исчисления. По-видимому, официально она была принята в Александрии во времена правления Птолемея Филадельфийского и в последующие годы распространилась оттуда по всему греческому миру, включая Аттику. Переход к ионической системе счисления произошел в золотой век древнегреческой математики и, в частности, при жизни двух величайших математиков античности. Есть нечто большее, чем просто совпадение, в том, что именно тогда Архимед и Аполлоний работали над усовершенствованием системы обозначения больших чисел. Архимед, придумавший схему октад (эквивалентную современному использованию показателей степени числа 10), гордо заявлял в своем сочинении «Псаммит» («Исчисление песчинок»), что может численно выразить количество песчинок, необходимых для того, чтобы заполнить всю известную тогда Вселенную. Изобретенная им система обозначения чисел включала число, которое ныне можно было бы записать в виде единицы, за которой следовало бы восемьдесят тысяч миллионов миллионов цифр.
С помощью простого введения диакритических знаков наподобие тех, которые греки применяли для обозначения тысяч, алфавитное обозначение целых чисел можно было бы легко приспособить для обозначения десятичных дробей, но этой возможностью они не воспользовались. Вместо этого для обозначения дробей греки использовали приемы древних египтян и вавилонян. Египетское влияние в Греции было достаточно сильным, чтобы навязать грекам употребление лишь аликвотных дробей, однако большие вычислительные удобства системы счисления вавилонян побудили живших позднее александрийских астрономов перейти к использованию шестидесятиричных дробей. Переняв систему счисления Древнего Вавилона, греки заменили месопотамскую клинопись своими буквенными обозначениями. Например, Птолемей записал длину хорды, стягивающей дугу в 120° окружности радиусом в 60 единиц, как RGNE?KG?•, т.е. 103 + 55/60 + 23/602 единиц. В более поздний период в вавилонской шестидесятиричной системе имелся специальный символ для обозначения «пустой» позиции, и греческие астрономы ввели для этой цели букву омикрон. Неясно, был ли такой выбор подсказан тем, что с этой буквы начиналось слово оуден (ничто). Сходство греческой буквы О с современным обозначением нуля может быть чем-то большим, чем случайное совпадение, но у нас нет точных данных, позволяющих утверждать это со всей определенностью.
Поскольку греки работали с обыкновенными дробями лишь эпизодически, они использовали различные обозначения. Герон и Диофант, самые известные арифметики среди древнегреческих математиков, записывали дроби в алфавитной форме, причем числитель располагали под знаменателем. Но в принципе предпочтение отдавалось либо дробям с единичным числителем, либо шестидесятиричным дробям.
Недостатки греческих обозначений дробных чисел, включая использование шестидесятиричных дробей в десятичной системе счисления, объяснялись отнюдь не пороками основополагающих принципов. Недостатки греческой системы счисления можно отнести скорее за счет их упорного стремления к строгости, которое заметно увеличило трудности, связанные с анализом отношения несоизмеримых величин. Слово «число» греки понимали как набор единиц, поэтому то, что мы теперь рассматриваем как единое рациональное число – дробь, – греки понимали как отношение двух целых чисел. Именно этим объясняется, почему обыкновенные дроби редко встречались в греческой арифметике. Кроме того, десятичные представления обыкновенных дробей в большинстве случаев бесконечны. А поскольку бесконечность была исключена из строгих рассуждений, теоретическая арифметика не нуждалась в такого рода представлениях. С другой стороны, областью, в которой практические вычисления испытывали величайшую потребность в точных дробях, была астрономия, а здесь вавилонская традиция была настолько сильна, что шестидесятиричная система обозначений угловых, дуговых и временных величин сохраняется и поныне.
Рим. Римские обозначения чисел известны ныне лучше, чем любая другая древняя система счисления. Объясняется это не столько какими-то особыми достоинствами римской системы, сколько тем огромным влиянием, которым пользовалась Римская империя в сравнительно недавнем прошлом. Этруски, завоевавшие Римскую империю в 7 в. до н.э., испытали на себе влияние восточно-средиземноморских культур. Этим отчасти объясняется сходство основных принципов римской и аттической систем счисления. Обе системы были десятичными, хотя в обеих системах счисления особую роль играло число пять. Обе системы использовали при записи чисел повторяющиеся символы. Старыми римскими символами для обозначения чисел 1, 5, 10, 100 и 1000 были, соответственно, символы I, V, X, Q (или A, или A) и f (или , или ). ). Хотя о первоначальном значении этих символов было написано много, их удовлетворительного объяснения у нас нет до сих пор. Согласно одной из распространенных теорий, римская цифра V изображает раскрытую руку с четырьмя прижатыми друг к другу пальцами и отставленным большим пальцем; символ X, согласно той же теории, изображает две скрещенные руки или сдвоенную цифру V. Символы чисел 100 и 1000, возможно, берут начало от греческих букв Q и f. Неизвестно, произошли ли более поздние обозначения C и M от старых римских символов или они акрофонически связаны с начальными буквами латинских слов, означавших 100 (центум) и 1000 (милле). Полагают, что римский символ числа 500, буква D, возник из половинки старого символа, обозначавшего 1000. Если не считать, что большинство римских символов скорее всего не были акрофоническими и что промежуточные символы для обозначения чисел 50 и 500 не были комбинациями символов чисел 5 и 10 или 5 и 100, то в остальном римская система счисления напоминала аттическую. Разумеется, в деталях они отличались. Римляне часто использовали принцип вычитания, поэтому иногда вместо VIIII использовали IX и XC вместо LXXXX; сравнительно позднее символ IV вместо IIII.
В целом римляне не были склонны заниматься математикой, поэтому не испытывали особой потребности в больших числах. Тем не менее для обозначения 10000 они эпизодически использовали символ , а для числа 100000 – символ . Половинки этих символов иногда использовались для обозначения чисел 5000 ( ) и 50000 ( ). Таким образом, в римских обозначениях число 6789 можно было бы записать как .
Дробей римляне избегали так же упорно, как и больших чисел. В практических задачах, связанных с измерениями, они не использовали дроби, подразделяя единицу измерения обычно на 12 частей, с тем чтобы результат измерения представить в виде составного числа, суммы кратных различных единиц, как это делается сегодня, когда длину выражают в ярдах, футах и дюймах. Английские слова «ounce» (унция) и «inch» (дюйм) происходят от латинского слова uncia (унция), обозначавшего одну двенадцатую основной единицы длины.
Обозначения чисел у древних евреев. Семитские народы могут претендовать на роль создателей алфавитного принципа обозначения чисел в том виде, как он использовался в ионической системе. Действительно, с небольшими модификациями этот принцип применялся евреями, сирийцами, арамейцами и арабами. И все же существует мало сомнений в том, что алфавитные обозначения чисел были заимствованы ими у древних греков, по-видимому из Милета, которые изобрели эти обозначения еще в 8 в. до н.э. У евреев использование алфавитных обозначений чисел окончательно вошло в обиход к 2 в. до н.э. Девять букв алфавита использовались для обозначения первых девяти целых чисел; еще девять букв означали первые девять кратных числа 10; остальные буквы использовались для обозначения сотен. Так как букв в алфавите для обозначения всех кратных числа 100 не хватало, в Талмуде числа, превосходящие 400, записывались путем комбинации: например, число 500 обозначалось символами, соответствующими числам 400 и 100, а 900 записывалось как 400 и 400 и 100. Позднее для обозначения чисел, кратных 100 и превосходящих 400, использовались окончательные варианты формы букв или других символов, в результате чего все девять кратных числа 100 получили свои индивидуальные обозначения в виде буквы или специального знака. (См. таблицу обозначений чисел.) Как и в ионической системе счисления, символы для обозначения первых девяти кратных числа 1000 были такими же, как символы, обозначающие первые девять чисел в разряде единиц. Число 6789 евреи записывали как . Так как запись числа 15 в обычном виде как 10 и 5 совпадает с первыми двумя буквами имени Бога Яхве, древние евреи записывали число 15 как 9 и 6. Высказывалось предположение, что по аналогичным причинам древние римляне избегали записывать число IV вместо IIII, т.к. символ IV совпадает с первыми двумя буквами старолатинского написания имени Юпитер.
Америка. Исследователи, путешествовавшие в 16 в. по Центральной Америке, обнаружили цивилизации с высокоразвитыми системами счисления, отличными от тех, которые были известны в Европе. Самыми важными элементами в системе счисления майя были использование позиционного принципа и символа нуля. Если отвлечься от того, что принятая у индейцев майя система счисления была не шестидесятиричной, а двадцатиричной и вместо 10 использовала вспомогательное основание 5, то в остальном принципы были аналогичны тем, которые ранее были в ходу у жителей Древнего Вавилона. В схеме майя точка означала единицу, а повторяющиеся точки – числа до четырех; пятерку обозначала горизонтальная черта, а две и три горизонтальные черты обозначали, соответственно, числа десять и пятнадцать. Для обозначения числа двадцать майя воспользовались позиционным принципом, используя точку, помещенную над символом нуля. (Последний имел вид .)
Числа в системе счисления древних майя записывались в столбец, причем верхние символы были старшими. Самая нижняя позиция соответствовала разряду единиц; «этажом выше» располагалось число двадцаток. Еще выше единица соответствовала не кратным числа 400, как можно было бы ожидать, а кратным числа 360. За исключением этого разряда, связанного, насколько можно судить, с календарными соображениями и продолжительностью года, все остальные более высокие позиции соответствовали степеням числа 20. Число 6789 в системе счисления, принятой у майя, записывалось как
Система счисления у ацтеков в Мексике была более последовательно двадцатиричной, чем у майя, но в остальном менее тонкой, так как не использовала ни позиционный принцип, ни специальный символ для нуля. Точка означала у ацтеков единицу, а для обозначения степеней числа 20 были введены новые знаки: флаг для 20, дерево для 400 и кошелек для 8000. При необходимости другие числа представлялись с помощью повторения этих символов, а от их чрезмерного повторения они избавлялись, вводя специальные промежуточные коллективные знаки: ромбовидный знак для 10 и фрагменты дерева для 100, 200 или 300.
До появления в Северной Америке европейцев индейцы не имели письменности. Исследования древних систем счисления показывают, что используемые названия чисел были в основном прилагательными и лишь в отдельных случаях достигали уровня абстракции, когда они становились существительными. Тем не менее с помощью рисунков или устно индейцы могли выразить число вплоть до миллиона. Системы составления чисел были самыми различными, но примерно половина из них по существу была десятичной.
Китай. Одна из древнейших систем счисления была создана в Китае, а также в Японии. Эта система возникла как результат оперирования с палочками, выкладываемыми для счета на стол или доску. Числа от единицы до пяти обозначались, соответственно, одной, двумя и т.д. палочками, выкладываемыми вертикально, а одна, две, три или четыре вертикальные палочки, над которыми помещалась одна поперечная палочка, означали числа шесть, семь, восемь и девять. (См. таблицу обозначений чисел.) Первые пять кратных числа 10 обозначались одной, двумя, ?, пятью горизонтальными палочками, а одна, две, три и четыре горизонтальные палочки, к которым сверху приставлялась вертикальная палочка, означали числа 60, 70, 80 и 90. Для обозначения чисел больше 99 использовался позиционный принцип. Число 6789 китайцы записали бы так: . Обозначения чисел с помощью палочек тесно связано со счетом на пальцах и счетной доске, но применялось оно также и в письменных вычислениях.
Во второй китайской системе счисления для обозначения первых девяти целых чисел или символов (см. таблицу обозначений чисел) используют девять различных знаков и одиннадцать дополнительных символов для обозначения первых одиннадцати степеней числа 10. В сочетании с умножением и вычитанием это позволяло записывать любое число меньше триллиона. Если один из символов, обозначающих первые девять целых чисел, стоит перед (при чтении слева направо) символом, означающим степень числа 10, то первое нужно умножить на второе, если же символ одного из девяти первых целых чисел стоит на последнем месте, то это число надлежит прибавить к обозначенному предыдущими символами. В такой системе счисления число 6789 выглядело бы так: , т.е. 6?1000 + 7?100 + 8?10 + 9.
Индия. Письменных памятников древнеиндийской цивилизации сохранилось очень немного, но, судя по всему, индийские системы счисления проходили в своем развитии те же этапы, что и во всех прочих цивилизациях. На древних надписях из Мохенджо-Даро вертикальная черточка в записи чисел повторяется до тринадцати раз, а группировка символов напоминает ту, которая знакома нам по египетским иероглифическим надписям. В течение некоторого времени имела хождение система счисления, очень напоминающая аттическую, в которой для обозначения чисел 4, 10, 20 и 100 использовались повторения коллективных символов. Эта система, которая называется кхарошти, постепенно уступила место другой, известной под названием брахми, где буквами алфавита обозначались единицы (начиная с четырех), десятки, сотни и тысячи. Переход от кхарошти к брахми происходил в те годы, когда в Греции, вскоре после вторжения в Индию Александра Македонского, ионическая система счисления вытеснила аттическую. Вполне возможно, что переход от кхарошти к брахми происходил под влиянием греков, но сейчас вряд ли возможно хоть как-то проследить или восстановить этот переход от древних индийских форм к системе, от которой произошли наши системы счисления. Надписи, найденные в Нана-Гат и Насике, относящиеся к первым векам до нашей эры и первым векам нашей эры, по-видимому, содержат обозначения чисел, которые были прямыми предшественниками тех, которые получили теперь название индо-арабской системы. Первоначально в этой системе не было ни позиционного принципа, ни символа нуля. Оба эти элементы вошли в индийскую систему к 8–9 вв. вместе с обозначениями деванагари (см. таблицу обозначений чисел). В индийской системе число 6789 записывалось бы как . Здесь мы впервые встречаемся с элементами современной системы счисления: индийская система была десятичной, цифровой и позиционной. При желании можно даже усмотреть некоторое сходство в начертании современных цифр и цифр деванагари.
Напомним, что позиционная система счисления с нулем возникла не в Индии, поскольку за много веков до этого она использовалась в Древнем Вавилоне в связи с шестидесятиричной системой. Поскольку индийские астрономы использовали шестидесятиричные дроби, вполне возможно, что это навело их на мысль перенести позиционный принцип с шестидесятиричных дробей на целые числа, записанные в десятичной системе. В итоге произошел сдвиг, приведший к современной системе счисления. Не исключена также возможность, что такой переход, по крайней мере отчасти, произошел в Греции, скорее всего в Александрии, и оттуда распространился в Индию. В пользу последнего предположения свидетельствует сходство кружка, обозначающего нуль, с начертанием греческой буквы омикрон. Однако происхождение индийского символа для нуля окутано тайной, так как первое достоверное свидетельство его появления в Индии датируется лишь концом 9 в. Как ни странно, ни греки, ни индийцы не включили в свои системы счисления десятичные дроби, но именно индийцам мы обязаны современной системой записи обыкновенных дробей с числителем, расположенным над знаменателем (но без горизонтальной черты, отделяющей числитель от знаменателя).
Аравия. Современную систему обозначения чисел часто называют арабской, хотя ясно, что она берет начало не из Аравии. До хиджры арабы записывали числа словами, но затем, как это делали ранее греки, они стали обозначать числа буквами своего алфавита. В 772 индийский трактат «Сидданта» был привезен в Багдад и переведен на арабский, после чего стали использоваться две системы записи чисел: (1) в астрономии по-прежнему употребляли алфавитную систему, (2) в торговых расчетах купцы стали применять систему, заимствованную из Индии. Но даже среди тех, кто пользовался индийской системой, начертания цифр, как и в Индии, сильно варьировали. Эти две системы счисления были широко распространены и после распада арабского халифата. В его восточной части пользовались системой, аналогичной той, которая и сейчас встречается в арабском мире. Число 6789 в этой системе записывается как . Однако обозначения чисел в Испании 10 в. настолько сильно отличались по своим начертаниям от приведенных выше, что казались никак с ними не связанными. В испанских обозначениях, получивших название «гобар» или «песчаных», число 6789 выглядело бы так: . Свое название эти обозначения получили потому, что ими пользовались при вычислениях на «песчаном абаке». Как свидетельствует Бируни, индийцы часто производили вычисления на песке, что, возможно, и послужило поводом для такого названия. Тем не менее само происхождение этих цифр, от которых в свою очередь произошли наши современные цифры, остается неизвестным.
Западная Европа. Первым европейским ученым, о котором достоверно известно, что он ввел в употребление в Европе арабские цифры, был Герберт, работавший в Испании и позднее (в 999-м) ставший папой Сильвестром II. В 12 в. Хуан из Севильи перевел на латынь трактат De numero indorum (Об индийских числах) арабского математика Аль-Хорезми. Когда в следующем веке индийские обозначения стали широко известными, новая система получила название алгоритм – от искаженного Аль-Хорезми. Через пару столетий европейские алгоритмики одержали верх и над абацистами, и над теми, кто пользовался римскими цифрами в вычислениях с целыми числами, но лишь с 1585 индо-арабская система обозначений, систематически расширяясь, стала использоваться и применительно к дробям. В том же году Симон Стевин опубликовал свой небольшой трактат De Thiende (Десятина), в котором он предложил записывать в виде или число, которое мы записали бы как 6789. В 17 в. вошла в употребление десятичная запятая (или точка), которой стали отделять целую часть числа от дробной, после чего европейцы отказались от предложенной Стевином индексации разрядов. После этих изменений развитие современной системы счисления завершилось. (Это отнюдь не означает, будто была достигнута полная стандартизация в названиях или обозначениях чисел. В Америке и Франции биллион означает тысячу миллионов, а в Англии и Германии – миллион миллионов; в континентальной Европе часто используется десятичная запятая, а в англосаксонских странах предпочитают ставить десятичную точку; англосаксы используют запятые, чтобы отделять степени тысячи, в некоторых странах для этой цели служит точка.).
anastasi-shherbakova.narod.ru
Значение чисел – Нумерология цифр – Как магия чисел даты рождения влияет на жизнь человека
«Магия» чисел
Таинственная магия чисел присваивает каждой цифре свойственную ей вибрацию, составленную из комбинации определенных свойств. Расшифровав значение цифр в дате рождения или имени, можно узнать архетипическое качество, воплощающее природные таланты, характер и судьбоносные знаки на пути человека.
Со времен Пифагора, каждой элементарной цифре приписывались специфические характеристики. Рассмотрим подробно значение цифр в нумерологии.
А вы знаете, что нумерологический профиль человека состоит из более чем 50 цифр, каждая из которых описывает определенный аспект его личности ?
Что означают цифры от 1 до 9 в нумерологии?
Как мы уже упоминали ранее, каждая цифра в нумерологии имеет строго определенное, "магическое" значение. Рассмотрим подробнее каждое из них:
| Значение числа 0 Олицетворяет абсолютное небытие, непроявленность материи. | Значение числа 1 Власть, могущество, мужество, отвага, жизненная стойкость. |
| Значение числа 2 Изящество, женственность, деликатность, гибкость, партнерство. | Значение числа 3 Фантазия, творчество; образ жизни, характерный для «звезды». |
| Значение числа 4 Устойчивость, последовательность, труд, терпение, организованность. | Значение числа 5 Мобильность, изменчивость, перемена мест, любознательность, сенсация. |
| Значение числа 6 Гармоничность, спокойствие, романтика, семейный очаг. | Значение числа 7 Путь исследователя, философский склад ума, самоанализ. |
| Значение числа 8 Материальность, мудрость, уверенность, компромисс. | Значение числа 9 Коммуникабельность, масштаб, универсальность, многообразие. |
Как производится расчет чисел в нумерологии?
Чтобы выяснить значение чисел любой величины, применяется метод сложения (нумерологической редукции). Эта методика приведения сложного к простому помогает сокращать все цифровые значения до простых чисел от 1 до 9. В ее основе лежит принцип, говорящий о том, что элементарные цифры - это исходные элементы, которыми можно выразить все числовое многообразие.
Например, произведя последовательно два сложения, число 88357 превращается в число 31, а затем в цифру 4.
- ШАГ 1. 88357 → 88357 → 8 + 8 + 3 + 5 + 7 = 31
- ШАГ 2. 31→ 3 + 1 = 4
Выполняя редукцию необходимо постоянно держать в уме одно важное правило: если на одном из шагов у вас получилось сочетание цифр 11,22,13,14,16 или 19 то дальнейшее сокращение производить не нужно. Вы получили особенное число.
Значение особых чисел в нумерологии
Числа, состоящие из сдвоенных цифр, такие как 11, 22, 33 имеют особый статус. Их называют господствующими числами, так как в них раскрывается больший потенциал, чем в остальных.
- Значение числа 11 Число 11 окутано мистической аурой и символизирует магическую силу, что может выражаться в чрезмерности и произволе. Удвоенная единица, усиленная потенциалом двойки. Единство противоположностей.
- Значение числа 22 Число 22 – двойка в квадрате не так идеальна, как 11, так как не построена на балансе антагонизмов. Число логики, закона, взвешенности поступков и поклонения.
- 13, 14, 16 и 19 рассматриваются в нумерологии как кармические числа.
Значение чисел в дате рождения
Нумерологический код, рассчитываемый по дате рождения, несет в себе сакральную информацию о судьбе человека. Следуя предназначенному пути, человек обладает уникальным шансом раскрыть удачу, дарованную свыше. Чтобы полностью понять тайную символику чисел даты вашего рождения, находят:
Значение цифр в жизни человека таит в себе неисчерпаемый объем знаний, подробнее о нем вы можете узнать из раздела, посвященного нумерологии даты рождения.
Значение чисел имени человека
Если цифры даты рождения определяют потенциальные возможности человека, то числа имени позволяют постичь скрытые способности, данные ему от рождения.
Нумерология имени оперирует тремя знаковыми числами:
Числа и цифры в квадрате Пифагора
Квадрат Пифагора представляет собой отдельную структуру в нумерологии чисел. Пифагор взял за основу значение чисел у египетских жрецов и объединил их с математическим аспектом квадратичной гармонии. На сегодняшний день для расчета квадрата Пифагора используется два способа:
- Методика, описанная нумерологом Дэвидом Филлипсом.
- Психоматрица - цифровой анализ А. Александрова.
С помощью квадрата Пифагора и Психоматрицы можно вычислить характерные особенности личности: психотип, степень коммуникативности, профессиональные наклонности, потенциал здоровья. Данная методика несколько отлична от классической, ее подробное описание вы можете найти на страницах нашего сайта.
www.numeroscop.ru
