Большая Энциклопедия Нефти и Газа. Построение конуса
прямой, наклонный и усеченный конус
Развертка поверхности конуса - это плоская фигура, полученная путем совмещения боковой поверхности и основания конуса с некоторой плоскостью.
Варианты построения развертки:
Развертка прямого кругового конуса
Развертка боковой поверхности прямого кругового конуса представляет собой круговой сектор, радиус которого равен длине образующей конической поверхности l, а центральный угол φ определяется по формуле φ=360*R/l, где R – радиус окружности основания конуса.
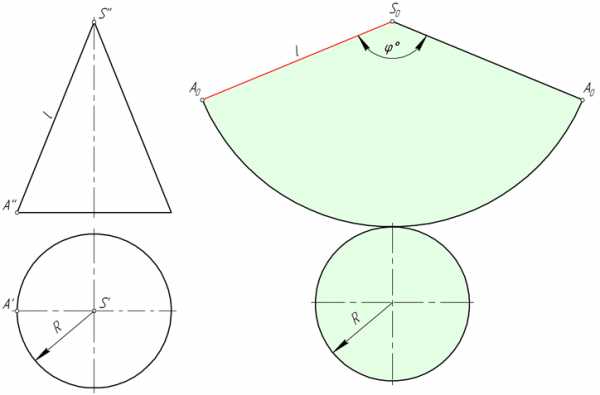
В ряде задач начертательной геометрии предпочтительным решением является аппроксимация (замена) конуса вписанной в него пирамидой и построение приближенной развертки, на которую удобно наносить линии, лежащие на конической поверхности.
Алгоритм построения
- Вписываем в коническую поверхность многоугольную пирамиду. Чем больше боковых граней у вписанной пирамиды, тем точнее соответствие между действительной и приближенной разверткой.
- Строим развертку боковой поверхности пирамиды способом треугольников. Точки, принадлежащие основанию конуса, соединяем плавной кривой.
Пример
На рисунке ниже в прямой круговой конус вписана правильная шестиугольная пирамида SABCDEF, и приближенная развертка его боковой поверхности состоит из шести равнобедренных треугольников – граней пирамиды.
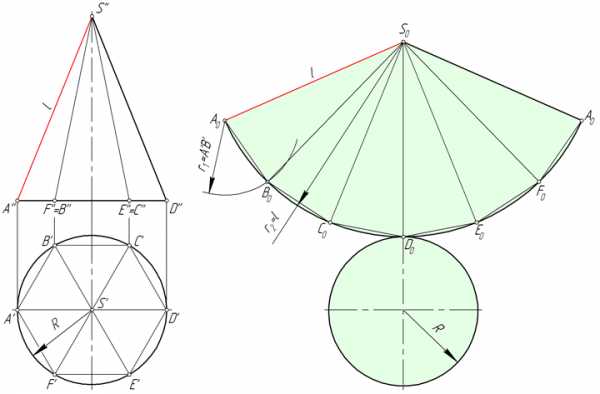
Рассмотрим треугольник S0A0B0. Длины его сторон S0A0 и S0B0 равны образующей l конической поверхности. Величина A0B0 соответствует длине A’B’. Для построения треугольника S0A0B0 в произвольном месте чертежа откладываем отрезок S0A0=l, после чего из точек S0 и A0 проводим окружности радиусом S0B0=l и A0B0= A’B’ соответственно. Соединяем точку пересечения окружностей B0 с точками A0 и S0.
Грани S0B0C0, S0C0D0, S0D0E0, S0E0F0, S0F0A0 пирамиды SABCDEF строим аналогично треугольнику S0A0B0.
Точки A, B, C, D, E и F, лежащие в основании конуса, соединяем плавной кривой – дугой окружности, радиус которой равен l.
Развертка наклонного конуса
Рассмотрим порядок построения развертки боковой поверхности наклонного конуса методом аппроксимации (приближения).
Алгоритм
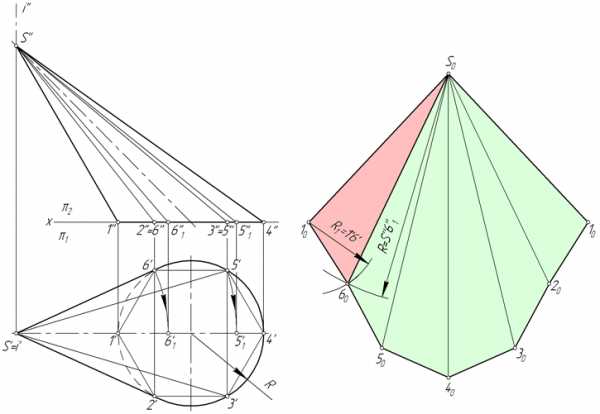
- Вписываем в окружность основания конуса шестиугольник 123456. Соединяем точки 1, 2, 3, 4, 5 и 6 с вершиной S. Пирамида S123456, построенная таким образом, с некоторой степенью приближения является заменой конической поверхности и используется в этом качестве в дальнейших построениях.
- Определяем натуральные величины ребер пирамиды, используя способ вращения вокруг проецирующей прямой: в примере используется ось i, перпендикулярная горизонтальной плоскости проекций и проходящая через вершину S.Так, в результате вращения ребра S5 его новая горизонтальная проекция S’5’1 занимает положение, при котором она параллельна фронтальной плоскости π2. Соответственно, S’’5’’1 – натуральная величина S5.
- Строим развертку боковой поверхности пирамиды S123456, состоящую из шести треугольников: S01060, S06050, S05040, S04030, S03020, S02010. Построение каждого треугольника выполняется по трем сторонам. Например, у △S01060 длина S010=S’’1’’0, S060=S’’6’’1, 1060=1’6’.
Степень соответствия приближенной развертки действительной зависит от количества граней вписанной пирамиды. Число граней выбирают, исходя из удобства чтения чертежа, требований к его точности, наличия характерных точек и линий, которые нужно перенести на развертку.
Перенос линии с поверхности конуса на развертку
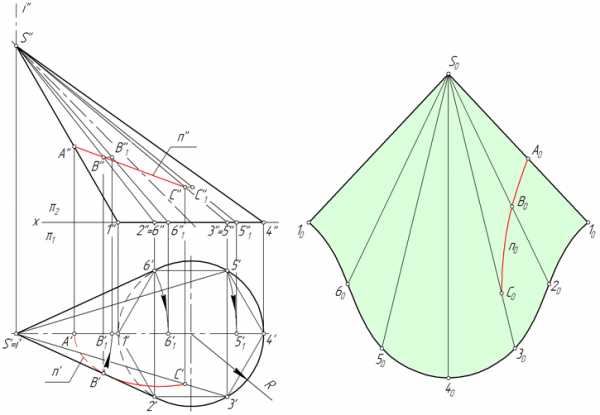
Линия n, лежащая на поверхности конуса, образована в результате его пересечения с некоторой плоскостью (рисунок ниже). Рассмотрим алгоритм построения линии n на развертке.
Алгоритм
- Находим проекции точек A, B и C, в которых линия n пересекает ребра вписанной в конус пирамиды S123456.
- Определяем натуральную величину отрезков SA, SB, SC способом вращения вокруг проецирующей прямой. В рассматриваемом примере SA=S’’A’’, SB=S’’B’’1, SC=S’’C’’1.
- Находим положение точек A0, B0, C0 на соответствующих им ребрах пирамиды, откладывая на развертке отрезки S0A0=S’’A’’, S0B0=S’’B’’1, S0C0=S’’C’’1.
- Соединяем точки A0, B0, C0 плавной линией.
Развертка усеченного конуса
Описываемый ниже способ построения развертки прямого кругового усеченного конуса основан на принципе подобия.
Алгоритм
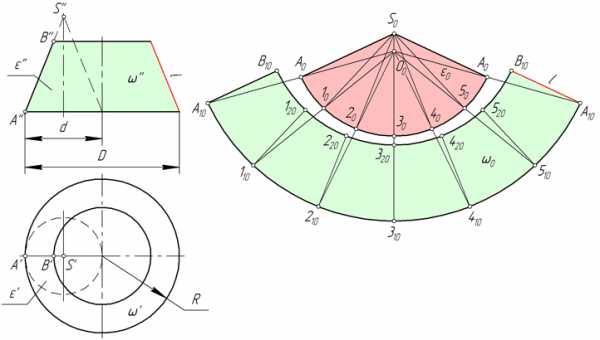
- Строим вспомогательный конус ε, подобный конусу ω, как это показано на рисунке выше. Для удобства построения величину диаметра d выбираем таким образом, чтобы соотношение t=D/d выражалось целым числом. В рассматриваемом примере t=2.
- Строим развертку боковой поверхности конуса ε – S0A01020304050A0 и на биссектрисе угла A0S0A0 отмечаем точку O0, выбрав ее расположение произвольно.
- Проводим прямые O0A0, O010, O020, O030, O040, O050, O0A0 и на них откладываем отрезки [O0A10]=t×|O0A0|, [O0110]= t×|O010|, [O0210]=t×|O020|, [O0310]=t×|O030|, [O0410]=t×|O040|, [O0510]=t×|O050|, [O0A10]=t×|O0A0| соответственно, где t=D/d. Соединяем точки A10, 110, 210, 310, 410, 510, A10 плавной линией.
- Из точек A10, 110, 210, 310, 410, 510, A10 проводим лучи, которые параллельны соответственно прямым A0S0, 10S0, 20S0, 30S0, 40S0, 50S0, A0S0, и на них откладываем отрезки A10B10, 110120, 210220, 310320, 410420, 510520, A10B10, равные l – образующей усеченного конуса. Проводим линию B10120220320420520B10.
ngeometry.ru
Построение развертки конуса. | МеханикИнфо
Развертка конуса. Построение развертки конуса. 4.40/5 (88.00%) проголосовало 5
Поверхность конуса состоит из боковой поверхности и поверхности основания.
Расчет развертки конуса.
Возьмем вертикальную и горизонтальную проекции конуса (рис. 1, а). Вертикальная проекция конуса будет иметь вид треугольника, основание которого равно диаметру окружности, а стороны равны образующей конуса. Горизонтальная проекция конуса будет изображаться окружностью. Если задана высота конуса Н, то длина образующей определяется по формуле:
т. е. как гипотенуза прямоугольного треугольника.
Обвернем картоном поверхность конуса. Развернув картон снова в одну плоскость (рис. 1, б), получим сектор, радиус которого равен длине образующей конуса, а длина дуги равна длине окружности основания конуса. Полную развертку боковой поверхности конуса выполняют следующим образом.
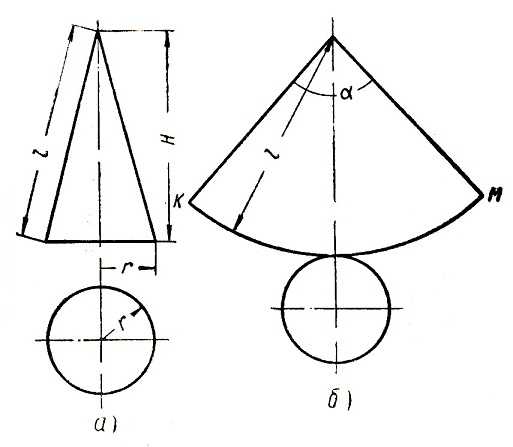
Рис. 1. Развертка конуса:
а — проекция; б — развертка.
Угол развертки конуса.
Принимая за радиус образующую конуса (рис. 1, б), на металле вычерчивают дугу, на которой затем откладывают отрезок дуги КМ, равный длине окружности основания конуса 2 π r. Длине дуги в 2 π r соответствует угол α, величина которого определяется по формуле:
где
г — радиус окружности основания конуса;
l — длина образующей конуса.
Построение развертки сводится к следующему. На длине ранее вычерченной дуги откладывается не часть дуги КМ, что практически является невозможным, а хорда, соединяющая концы этой дуги и соответствующая углу α. Величина хорды для заданного угла находится в справочнике или проставляется на чертеже.
Найденные точки КМ соединяются с центром окружности. Круговой сектор, полученный в результате построения, будет развернутой боковой поверхностью конуса.
mechanicinfo.ru
Построение конуса с вырезом - Чертежик
Построение конуса с вырезом выполняется методом секущих плоскостей.
Задание для построения:
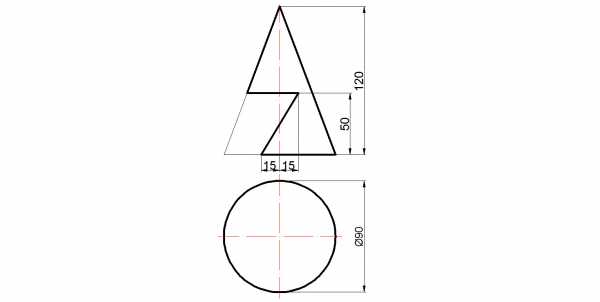Задание на построение конуса с вырезом1.) Проводятся секущие плоскости (обозначил разными цветами) и назвал a,p,k и m.
Расстояние между ними произвольное. Количество плоскостей произвольное Чем больше их, тем точнее линия пересечения.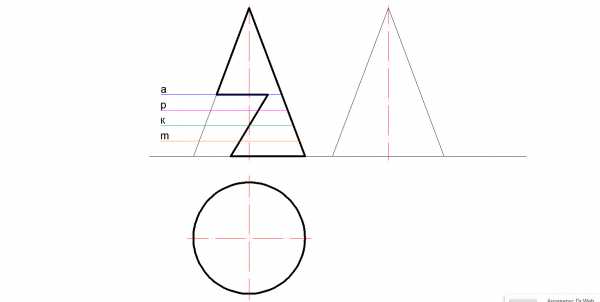
2.) Определяются точки на виде сверху.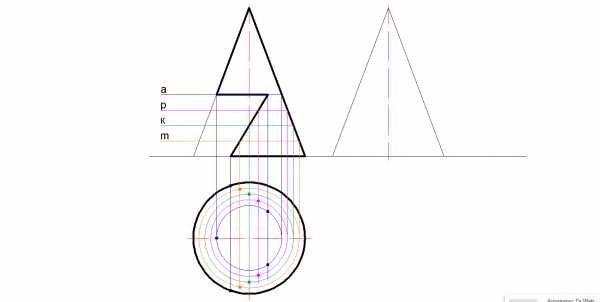
3.) Секущие плоскости продливают до вида слева (правый рисунок).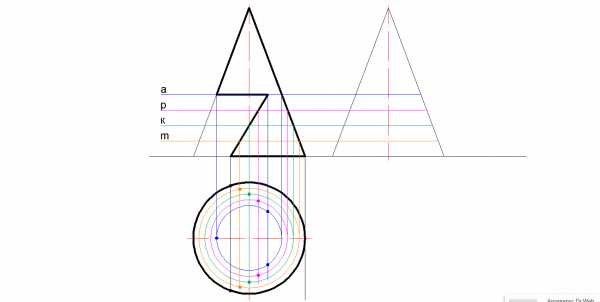
4.) От точек чертятся прямые, до оси.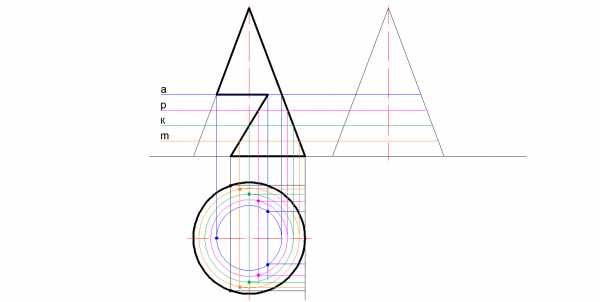
5.) Циркулем или под 45 град. переносятся на вид слева (правый рисунок). Вместе пересечения прямых ставятся точки.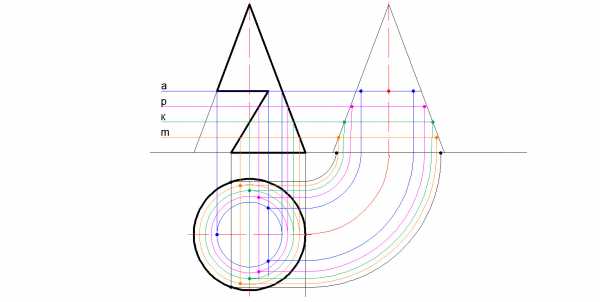
6.) Все точки соединяются плавной линией.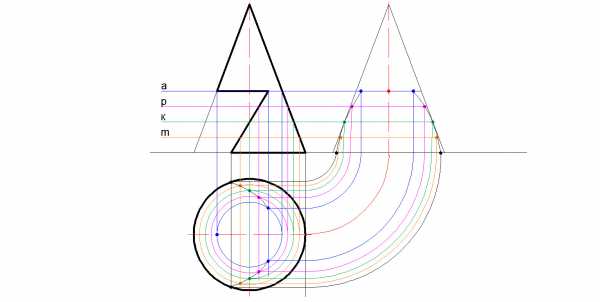
7.) Обводятся контуры фигуры с указанием видимых и невидимых линий.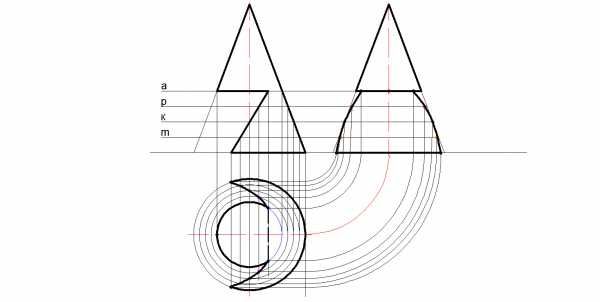
В видео предложено пошаговое построение.
Построение развертки конуса - Чертежик
Построение развертки конуса осуществляется предварительно с ознакомлением задания.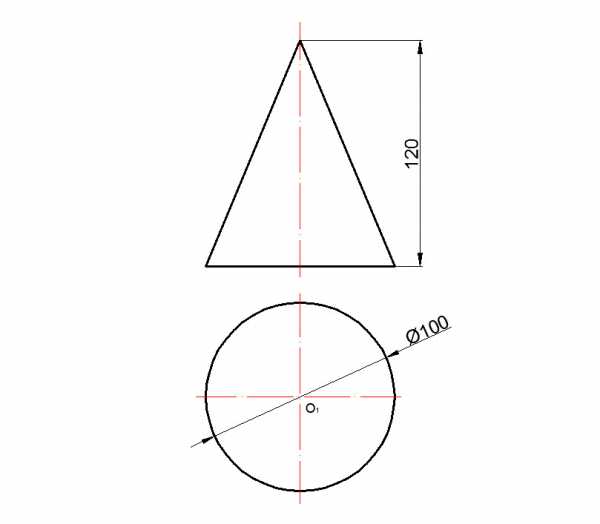
1. Строится вид слева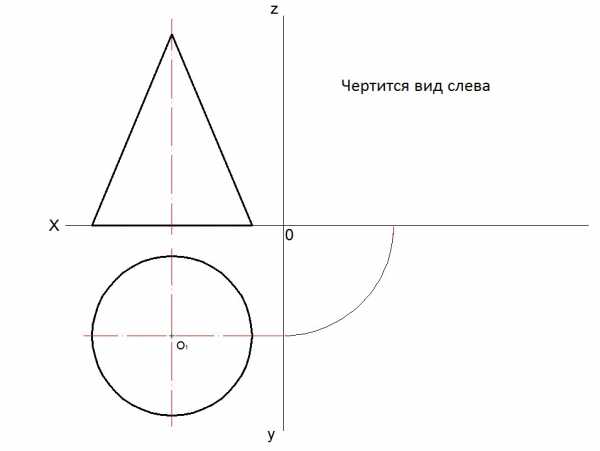
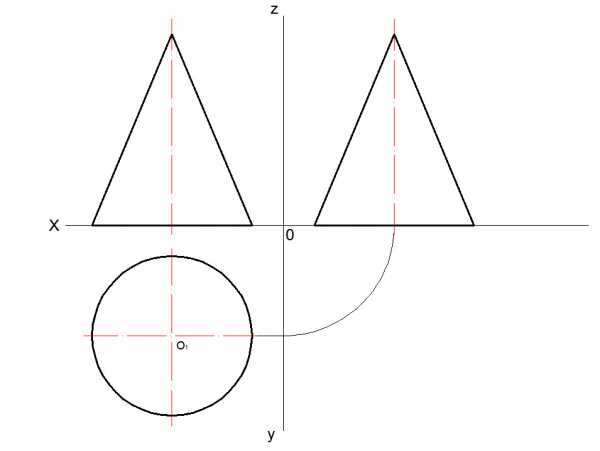
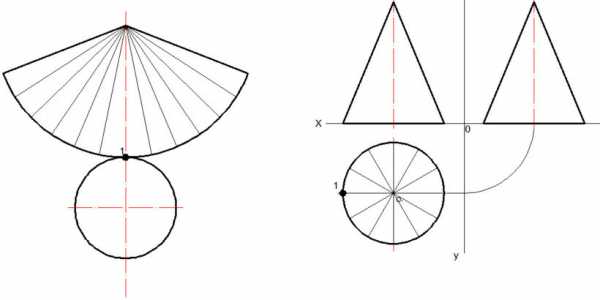
2.) Вид сверху, т. е. основание, делится на 12 частей.
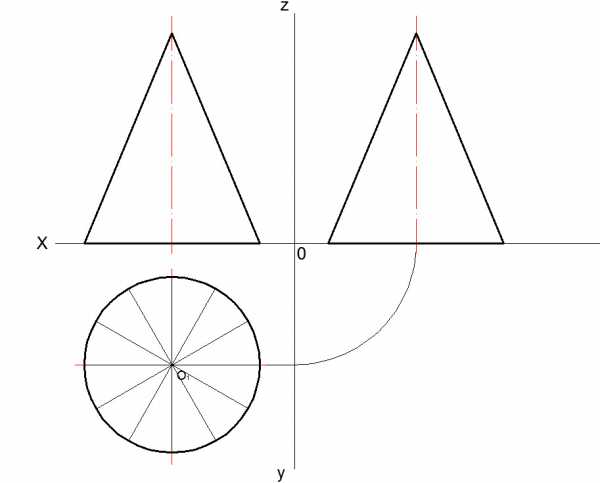
3.) Чертится дуга. Радиус равен расстоянию от вершины до края основания на виде спереди (профильный вид).
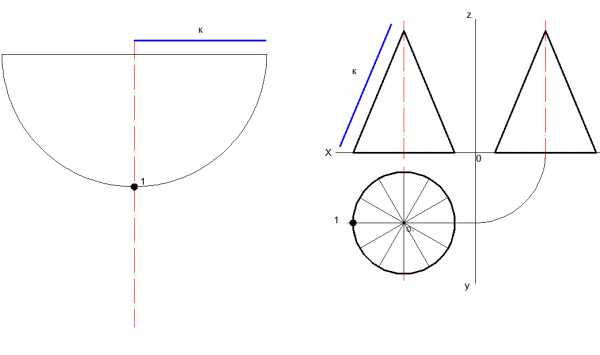
4.) Переносятся 12 частей на развертку. (Отмеряется расстояние между соседними частями на виде сверху циркулем)
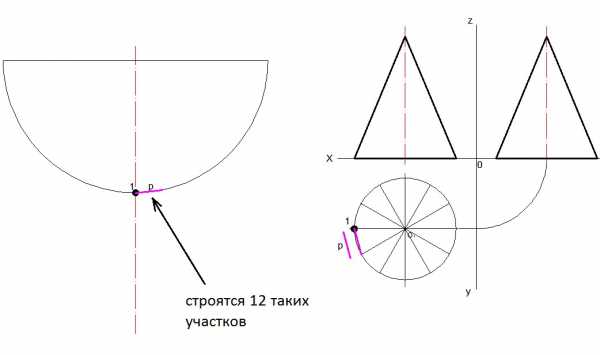
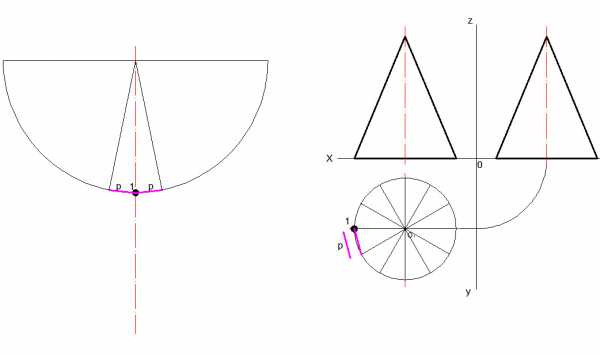
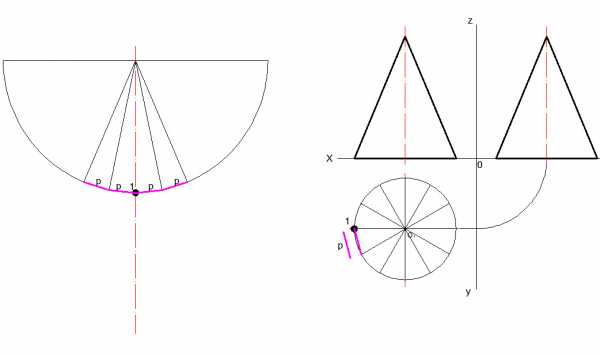
5.) После построения 12 частей дополнительные линии удаляются.
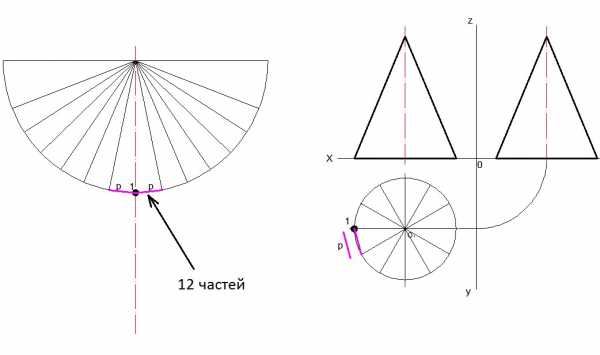
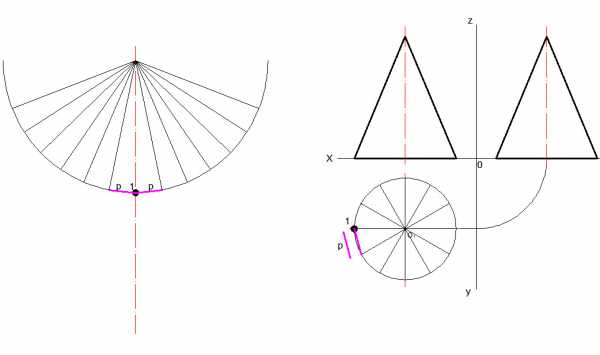
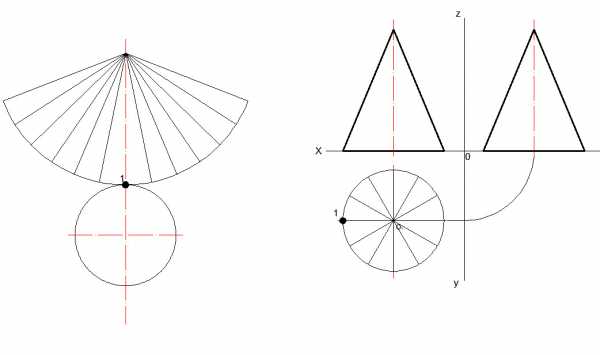6.) Последним шагом является обведение контура фигуры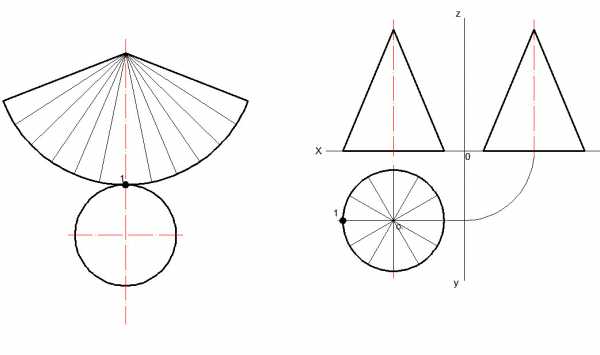
Также Вам советую почитать развертку усеченного конуса
Навигация по записям
chertegik.ru
Построение - конус - Большая Энциклопедия Нефти и Газа, статья, страница 1
Построение - конус
Cтраница 1
Построение конуса начинают с основания. Далее из центра эллипса откладывают высоту конуса. [1]
Для построения конусов с осями cklt pt и a1ml делают засечки: из точки b радиусом, равным ab, на оси cfej в точке с; из точки т радиусом, равным lab, на оси pt в точке р и из точки ег радиусом, равным Заб, на оси alml в точке тг. Дальнейшее построение усеченных конусов на этих трех осях аналогично построению первого усеченного конуса на оси agi. Из точки g вверх откладывают отрезок gxlt принимаемый из условия размещения фланца и сварных швов равным 100 мм. Проведя из точки хг горизонтальную прямую до пересечения ее с продолжением прямой hql в точке f и соединив точки ft и g, получают контур fxLgh большого цилиндрического концевого звена V. Малое концевое цилиндрическое звено VI строится аналогично. [2]
При построении конуса расширения должны быть учтены два обстоятельства. Во-первых, в процессе расширения большая часть металла как бы висит в воздухе. Это делает процесс неустойчивым и он легко может нарушиться. Поэтому следует, по возможности, применять минимальное расширение. При этом необходимо также учитывать то, что при большем расширении часть цилиндрического участка оправки будет находиться в следующем участке деформации гильзы. Во-вторых, после значительной переменной деформации в конусе прошивки металл может сравнительно свободно и легко расширяться. Поэтому угол наклона образующей конуса расширения может быть больше угла наклона образующей конуса осаживания. [3]
Огужит для построения трехмерного твердотельного конуса. [4]
Приведенному только что построению конусов вращения, касающихся трех данных плоскостей, пересекающихся в одной точке, соответствует на шаре построение малых кругов, касающихся трех данных больших кругов, не проходящих через одну точку. [5]
Что же касается операции построения конуса, то в случае пространства с отмеченной точкой мы приходим к понятию приведенного конуса. [6]
Это обстоятельство в дальнейшем нами будет использовано для построения конуса прогноза. [7]
Такой подход менее трудоемок и более точен, чем построение конусов способом триангуляции. [9]
Такой подход менее трудоемок и более точен, чем построение конусов способом триангуляции. [11]
Если теперь представить два начальных конуса в их проекции на плоскость, содержащую оси начальных конусов ( рис. 677), то построение конусов, на поверхности которых лежат торцовые поверхности зубьев, может быть сделано следующим образом. [13]
Вычислительная реализация конструкции ( 9) будет рассмотрена ниже; она довольно проста ( см. стр. Построение конуса К ( t) поясним рис. 3, на котором сплошными линиями изображены / - допустимые направления смещения, а штриховыми - недопустимые. [14]
Рисунок призмы выполнен в изометрической проекции. На рис. 141, а-г дано построение конуса во фронтальной диметрии. Как видно из рисунков, аксонометрические проекции геометрических тел выполняют в такой последовательности: проводят оси заданной аксонометрической проекции; строят основания геометрических тел; выполняют боковую поверхность; стирают лишние линии, рисунок обводят мягким карандашом и наносят теневую штриховку. Теневая штриховка играет очень большую роль: благодаря правильному распределению светотени зрительно воспринимается объемная форма предмета. Светотень - это распределение света на поверхности предмета, которое зависит от освещенности. Принято, что предмет освещен слева и сверху, поэтому наиболее светлыми изображают поверхности предмета, расположенные слева, и верхние его основания. Одним из распространенных приемов нанесения светотени является штриховка. [15]
Страницы: 1
www.ngpedia.ru
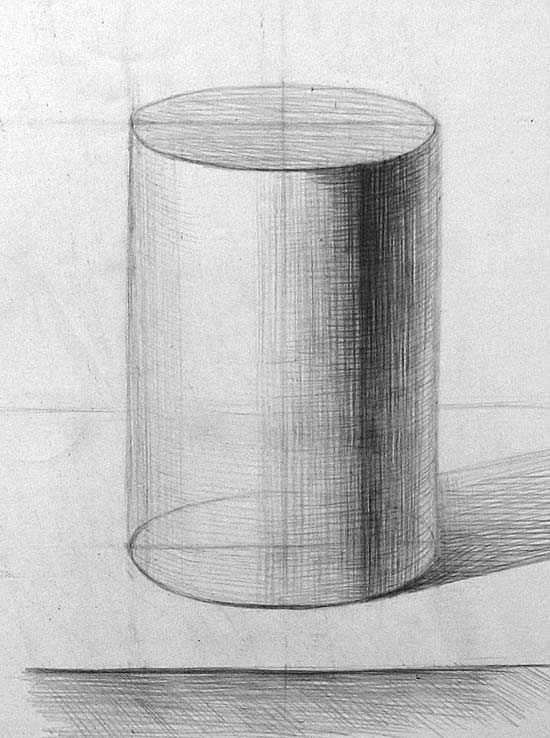
| Рисунок геометрических тел вращения, а именно конуса, цилиндра, шара, выполняется после того, как освоен рисунок куба. Сначала объёмные геометрические фигуры рисуют по отдельности, затем ставится натюрморт из геометрических тел. На примере изображения геометрических тел вращения усваиваются основные навыки академического рисунка. Для того, чтобы успешно рисовать сложные формы, сначала следует добиться грамотного выполнения простых заданий и хорошего уровня их выполнения. Любую форму, которую мы рисуем, при анализе можно представить как состоящую из простых геометрических форм, подход к изображению такой же, как при рисунке простых геометрических форм. Любой рисунок начинающим следует вести исключительно с натуры. Модели гипсовых геометрических тел можно купить или изготовить самостоятельно из плотной бумаги или картона. Срисовывание с пособий, фотографий не имеет смысла и не приносит никакой пользы. Представленные мной примеры могут послужить в помощь для самостоятельного обучения или помочь при выполнении домашних заданий по рисунку, но всё же лучше всего заниматься с преподавателем. Если вы живёте в Москве, то у вас есть возможность брать индивидуальные уроки рисунка у автора статьи. Рисунок конусаКонус представляет собой симметричное тело вращения, образующая конуса начинается в его вершине, совпадающей с осью вращения и заканчивается в основании. В нашем случае конус прямой, его ось перпендикулярна основанию.
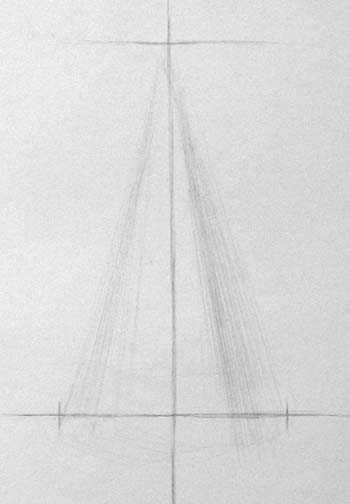
При рисовании конуса сперва намечаем место и размер изображения в листе. Конус не должен быть слишком большим или маленьким, разместить его следует выше середины листа. Оптически верх конуса легче, вокруг него больше свободного пространства, поэтому конус в рисунке следует разместить выше, чем, это делается обычно.
Затем отмечаем засечкой самую верхнюю часть конуса и проводим горизонтальную ось основания. Определив таким образом высоту, определяем, насколько ширина основания меньше высоты. Рисуем засечки, ограничивающие ширину основания. При этом учитываем, что эллипс, после того, как он будет построен, немного увеличит высоту конуса. Только после того, как определена высота и ширина, по центру проводим вертикальную ось симметрии.
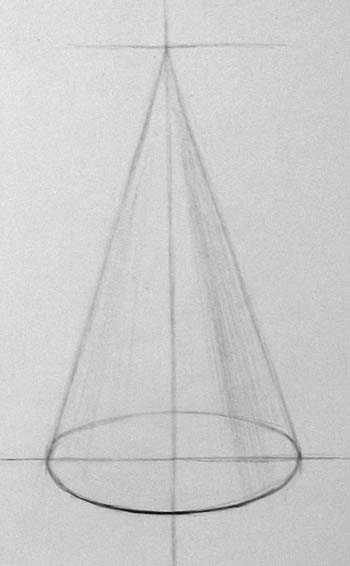
Соединяем вершину конуса с основанием. Линии с краю являются самыми удалёнными от рисовальщика поверхностями, поэтому их следует рисовать светлыми. Следующий этап - построение эллипса. При построении эллипса важно точно определить его раскрытость, насколько малый диаметр (видимый вертикальный размер) меньше, чем его ширина. Чтобы передать объём в линии, ближнюю часть овала сделаем темнее.
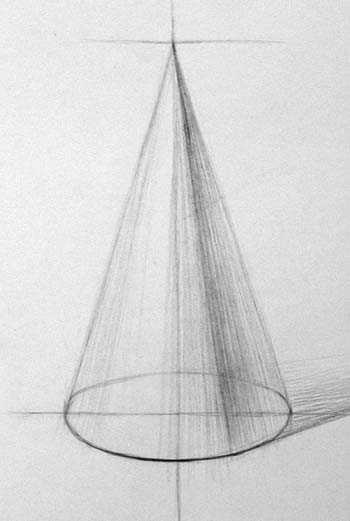
После того, как построение проверено, можно продолжить изображение объёмной формы конуса. Сперва находим границу света и тени. Граница представляет собой прямую линию, идущую от вершины к точке в основании. Постарайтесь верно определить, каково соотношение части, видимой на свету и части в тени. В верхней части линия немного чётче, в нижней части конуса она более плавно размыта к краям. Связано это с тем, что ближе к вершине конуса форма заворачивается сильнее, она почти приближается к угловой форме, какую мы видим на примере куба. Теневая поверхность удаляется от нас, дальний край по закону воздушной перспективы будет светлее. Освещённая часть удаляется от зрителя, поэтому, в соответствии с законами воздушной перспективы, она будет темнее. На границе света и тени мы видим полутон, промежуточную поверхность между светом и тенью, он относится к свету, но темнее, чем освещённая часть предмета, т. к. угол падения лучей света здесь небольшой. Падающая тень темнее тени собственной. Она лежит на горизонтальной поверхности, передняя часть тени темнее. Штрих кладём по форме, сначала в направлении лучей, идущих от вершины к основанию.
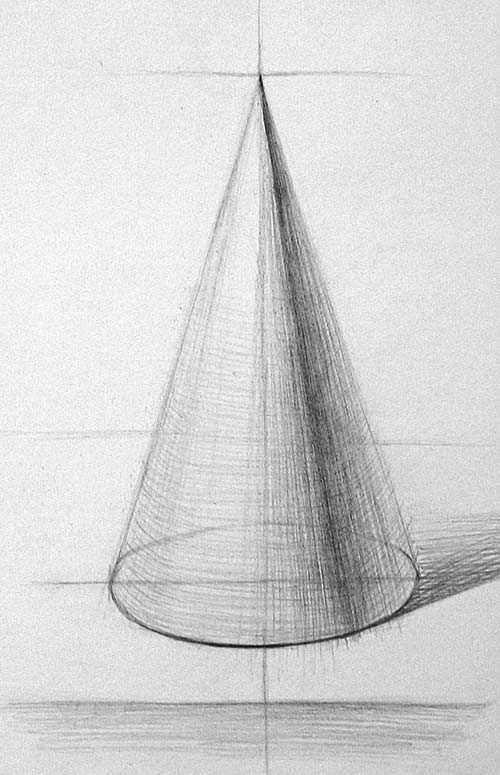
Для лучшей передачи формы введём горизонтальные линии штриховки, показывающие сечение формы по горизонтали. Особенно важно показать, как форма заворачивается по краям. На завершающем этапе работы уточняем тональные отношения и форму. Освещённая часть чуть темнее снизу, сверху выше контраст света и тени. Теневая часть конуса снизу подсвечена рефлексом от поверхности стола, также имеется рефлекс, проходящий по дальнему краю формы.
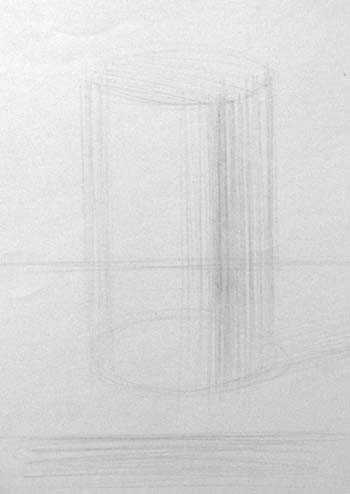
Рисунок цилиндраЦилиндр представляет собой простое тело вращения, у которого диаметр верхнего и нижнего основания равны, а плоскости оснований параллельны друг другу. Образующая представляет собой вертикальную линию, перпендикулярную основанию, которая вращается по окружности.
Последовательность работы над цилиндром такая же, как над рисунком конуса. Сначала намечаем место цилиндра в листе, сразу же легким штрихом выявляем объёмную форму.
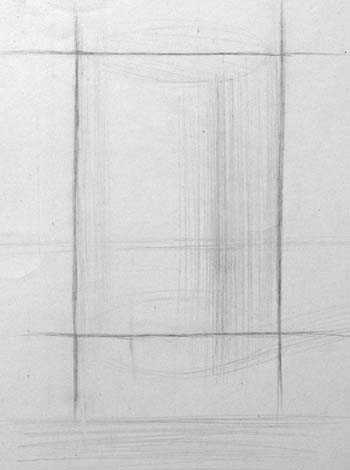
Затем работа ведётся последовательно, от большого к малому, от целого к детали. Старайтесь не давить излишне на карандаш, особенно при рисовании вспомогательных линий построения. Ластиком пользуйтесь как можно меньше. Если хотите поправить рисунок, то сначала обязательно нарисуйте правильную линию и только после того, как верная линия нарисована, можно стереть неверную. Когда стирают линию, а потом рисуют заново, то, как правило, повторяют уже сделанную ошибку. Сначала определяем высоту, а затем ширину цилиндра, насколько она меньше. Для сравнения высоты с шириной берите за основу расстояние между нижними краями эллипсов в центральной части цилиндра.
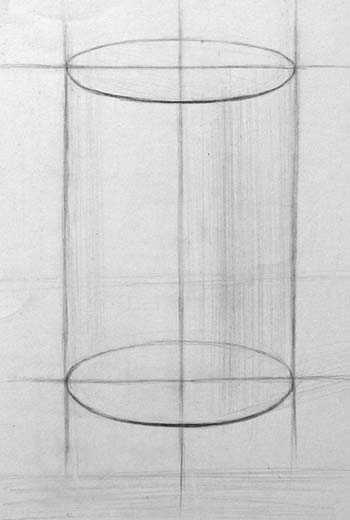
После того, как найдены основные пропорции, рисуем осевую линию. Ось симметрии делит цилиндр ровно пополам. Построение эллипсов начинаем с верхнего. Нам хорошо видно, как он развёрнут. Нижний эллипс развёрнут больше, чем верхний, в соответствии с законами перспективы.
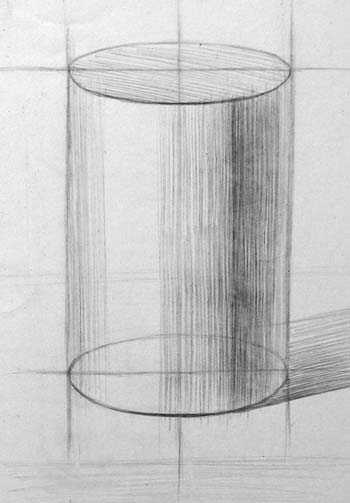
Граница светотени у цилиндра проходит по вертикальной линии. Форма меняется плавно, поэтому границы размыты. Штрих кладём по форме, в вертикальном направлении. Удаляющиеся поверхности на свету становятся темнее, а в тени, наоборот, светлее. Верхнее основание оказывается в полутоне, если освещение преимущественно сбоку. Штрих этой горизонтальной плоскости аналогичен штриховке верхнего основания куба. Передний край падающей тени берёт своё начало от точки границы светотени в основании цилиндра, а дольний край тени начинается от аналогичной точки на невидимой стороне.
На завершающем этапе работы уточняем форму штрихом в горизонтальном направлении. Верхняя часть чуть ближе к свету, она будет светлее. Теневая часть подсвечена снизу, а сверху тень в контрасте с верхним основанием. Поэтому самая тёмная часть тени окажется вверху.
Рисование шараГеометрическая форма шара самая простая из всех фигур, но для рисунка шар является самым сложным заданием. В первую очередь, начинающим сложно нарисовать ровный круг, трудно добиться плавных тональных переходов при штриховке, чтобы шар на рисунке не имел вмятин. Шар можно осветить естественным светом от окна или мягким светом с рассеивателем. Такой свет лучше, он не даёт резких теней.
При освещении лампой накаливания контраст сильнее, часто это приводит к тому, что начинающие изображают шар слишком тёмным, как будто он не из гипса, а из свинца.
Ниже представлен готовый рисунок шара. Изображения поэтапного ведения работы, построения теней, объяснения природы рефлексов появятся на сайте позже.
После того, как освоен рисунок геометрических тел по отдельности, можно приступить к рисованию группы из геометрических тел. Как правило, композиция включает в себя куб или параллелепипед, 1-2 тела вращения и шар. Рисунок кувшина также выполняется после того, как ученик умеет изображать простые геометрические формы. Разрешено копирование статей, только при наличии активной (кликабельной) ссылки на страницу-источник сайта Дениса Гаврилова gavrilovart.ru и при указании авторства. Ссылка должна находиться непосредственно рядом с материалом, должна быть видимой и прямой (без использования java-скриптов).Запрещено каким-либо образом изменять, затирать, отрезать копирайты на копируемых с моего сайта фотографиях или иллюстрациях.
|
gavrilovart.ru
РАЗВЕРТКА УСЕЧЕННОГО КОНУСА ПОСТРОЕНИЕ ЧЕРТЕЖА, Сечение прямого кругового конуса | Не ври
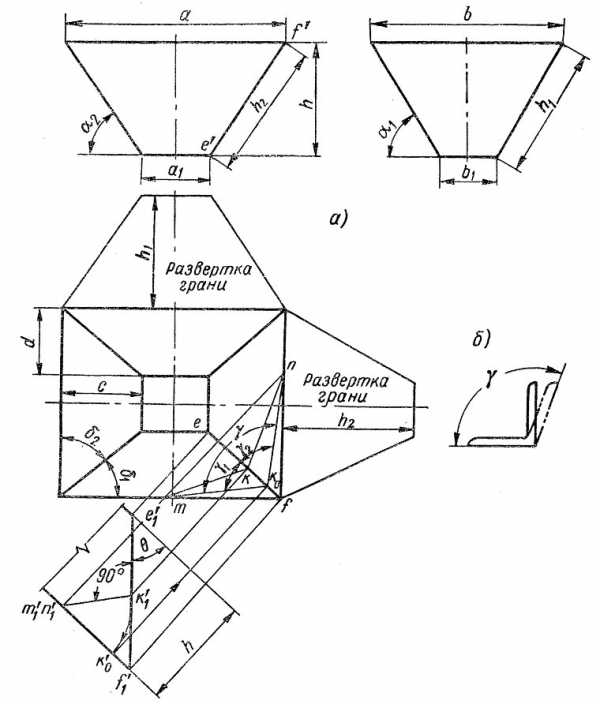Построить усечённый конус ABCD в натуральную величину (См. чертёж). Усечённый конус с доступной вершиной: Конус, при построении которого можно определить положение вершины. Конус со смещёной вершиной строится так же, как усечённый конус со смещёнными основаниями, по принципу триангуляции, с поочерёдным восстановлением высот от вида сверху.
В этих случаях применяется прямая, с вертикалью, верхняя точка вертикали соответствует высоте объекта. Для удобства, от можно откладывать половину длины окружности, в обе стороны от осевой линии конуса. При помощи нитки, длина которой равна длине окружности. Разделить окружность на 12 или более равных частей, и отложить их на дуге поочерёдно. Снять размер AA1-AA2, из точки AA1 поставить «примерную точку», сделав отмашку циркулем.
Построение разверток тел вращения
Построить вид сверху (см.чертёж). Поделить верхнее и нижнее основание на равные части A0-6 и B0-6, соединив соответствующие точки отрезками. Построить вертикаль A0-B0. (В рассматриваемом случае, верхняя плоскость смещена влево так, что точки A и D находятся на одной вертикали. Аналогичным образом продолжить построение до получения половины, либо цельной развёртки.
Построение развёртки цилиндра
Следует помнить: Независимо от того, является рассматриваемая поверхность развертываемой или неразвертываемой, графически может быть построена только приближенная развертка. Поэтому для получения поверхности из такой развертки, кроме изгибания, необходимо произвести частичное растяжение и сжатие отдельных ее участков.
Для создания развёртки, начертим четырёхугольник ACDE в натуральную величину (см.чертёж). Проведём перпендикуляр BD, из плоскости AC в точку D, отсекая от построения прямую часть цилиндра ABDE, которую можно достроить по мере надобности. Из центра плоскости CD (точка O) проведём дугу, радиусом в половину плоскости CD, и разделим её на 6 частей. Развёртка конуса может быть выполнена двумя способами. Если известен размер стороны конуса, из точки O, циркулем чертится дуга, радиусом равным стороне конуса.
Усечённый конус с непараллельными основаниями
Во всех иных случаях конус строится по принципу триангуляции (см. далее). Окружность поделить на равные части (в приведённом примере показано деление одной четверти). Снять размер AD и построить произвольную вертикаль AA0-AA1. Используя вышеприведённую технику, можно построить развёртку практически любого объекта со сложной топографией.
Развертка конуса строится таким же способом, который используются при развертывании боковой поверхности пирамиды — способом треугольников. Но прежде чем приступить к изготовлению, надо сделать выкройку (или развертку) для материала. В интернете есть всякие программы для расчета таких разверток. Однако задача настолько просто решается, что вы быстрее рассчитаете ее с помощью калькулятора (в компьютере), чем будете искать, скачивать и разбираться с этими программами.
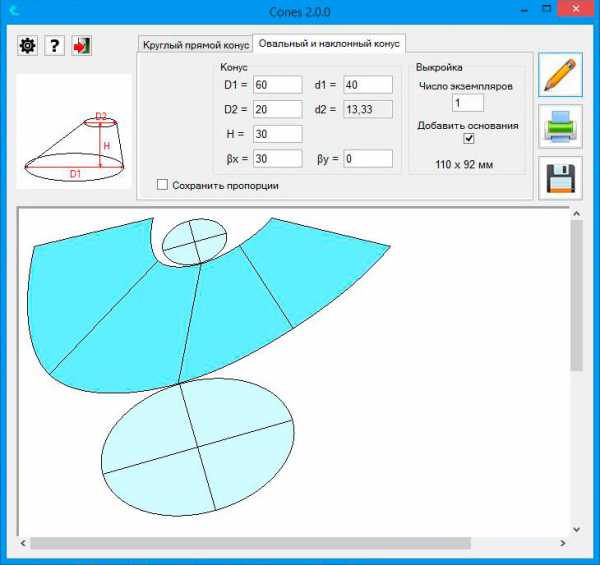
Совершенно понятно, что в качестве заготовки будет выступать круг с вырезанным сегментом. По теореме Пифагора рассчитаем диаметр круга заготовки (не путайте с радиусом готового конуса). А длина окружности готового конуса равна Пи*D. Обозначим ее Lm. Она, естественно, меньше чем длина окружности заготовки. Если 360 градусов дают нам полную окружность заготовки, то искомый угол должен дать длину окружности готового конуса.
Не забудьте оставить небольшую полоску материала для нахлеста (если крепление конуса будет внахлест). После соединения сторон вырезанного сектора получим конус заданного размера. Но мы прибегнем к тем же простым математическим построениям на основе теоремы Пифагора и подобия. Теперь зная общую высоту конуса, мы можем свести решение задачи к предыдущей.
Горизонтальная плоскость уровня λ пересекает боковую поверхность конуса по окружности — параллели.I. I, а. Фронтальная проекция сечения выявлена отрезком A2В2, сливающимся с проекцией δ2 и равным большой оси эллипса. Пристроив к любой точке линии сечения, например к точке В, соответствующей точкой эллипс — сечение, получают развертку поверхности усеченного конуса.III.
Построение развертки боковой поверхности аналогично приведенному в предыдущем примере. 6. Обозначаем точки пересечения секущей плоскости с ребрами призмы на фронтальной проекции призмы и по линиям связи находим эти точки на оставшихся проекциях. Таким образом, получаем искаженные фигуры сечения призмы плоскостью в проекциях.
Развертка усеченной призмы
8. Для построения из каждой точки фронтальной проекции поднимаем перпендикуляры. 9. Переносим соответствующие размеры с горизонтальной проекции призмы на новую горизонтальную проекцию (т. к. натуральный вид сечения мы строим способом перемены плоскостей проекций).
10. Развертку усеченной призмы будем строить на одной линии координатными осями проекций призмы. Так будет меньше вспомогательных построений. Боковая поверхность усеченного конуса не имеет плоских элементов, т.к. является кривой поверхностью. Впишите в конус многогранник. Для этого на горизонтальной проекции окружность нижнего основания конуса разделите на дуги 12(1₁2₁), 23(2₁3₁) и т.д.
В результате получите вписанную в данный усеченный конус восьмигранную усеченную пирамиду. Грани ее представляют собой трапеции, у которых стороны основания – хорды 1₁2₁, 6₁7₁ и т.д., а две другие противоположные стороны – боковые ребра 1₁6₁, 2₁7₁ и т.д. Эти грани-трапеции и являются плоскими элементами, которые совмещаются с плоскостью чертежа при развертке.
Построение чертежа основы конической юбки
Развертка многогранника представляет собой плоскую фигуру, полученную при совмещении всех его граней с плоскостью. Следовательно, построение развертки многогранника сводится к построению истинных величин его граней. Выполнение этой операции связано с определением натуральных величин его ребер, которые являются сторонами многоугольников – граней, а иногда и некоторых других элементов.
У изображенной на рисунке пирамиды стороны основания являются горизонталями и проецируются на плоскость П1 в истинную величину. Следующая операция состоит в построении каждой боковой грани как треугольника по трем сторонам.
Получим развертку боковой поверхности усеченного цилиндра. Для построения развертки пирамиды (рис. 1) необходимо предварительно определить натуральные величины боковых ребер и сторон основания. Точки AA1-AA4 соединить отрезками с точкой A. Провести ось O, из центра которой провести перпендикуляр O-O1, высотой равной высоте конуса.
Похожие материалы:
- Мягкий аутизм и аутоподобное поведение Может ли ребенок вырасти из аутизма, или можно ли его вылечить? В этой главе рассмотрены возможные границы аутизма. Термин может касаться […]
- Компетенция — Википедия Компетенция» и «Компетентность»: к вопросу использования понятий в современном российском образовании. Как правильно: уровень языковой […]
- Где получить справку 070у? Итак, мы подробно рассмотрели справку 070у, которая выдается для получения путевки в санаторно-курортные учреждения. Срок действия справки […]
velnosty.ru
