Содержание
Выкройка для конуса | Математика для ювелиров
Вместо слова «выкройка» иногда употребляют «развертка», однако этот термин неоднозначен: например, разверткой называют инструмент для увеличения диаметра отверстия, и в электронной технике существует понятие развертки. Поэтому, хоть я и обязан употребить слова «развертка конуса», чтобы поисковики и по ним находили эту статью, но пользоваться буду словом «выкройка».
Построение выкройки для конуса — дело нехитрое. Рассмотрим два случая: для полного конуса и для усеченного. На картинке (кликните, чтобы увеличить) показаны эскизы таких конусов и их выкроек. (Сразу замечу, что речь здесь пойдет только о прямых конусах с круглым основанием. Конусы с овальным основанием и наклонные конусы рассмотрим в следующих статьях).
1. Полный конус
Обозначения:
- — диаметр основания конуса;
- — высота конуса;
- — радиус дуги выкройки;
- — центральный угол выкройки.
Параметры выкройки рассчитываются по формулам:
;
;
где .
2. Усеченный конус
Обозначения:
- — диаметр большего основания конуса;
- — диаметр меньшего основания конуса;
- — высота конуса;
- — радиус внешней дуги выкройки;
- — радиус внутренней дуги выкройки;
- — центральный угол выкройки.
Формулы для вычисления параметров выкройки:
;
;
;
где .
Заметим, что эти формулы подойдут и для полного конуса, если мы подставим в них .
3. Угол при вершине конуса
Иногда при построении конуса принципиальным является значение угла при его вершине (или при мнимой вершине, если конус усеченный). Самый простой пример — когда нужно, чтобы один конус плотно входил в другой. Обозначим этот угол буквой (см. картинку).
В этом случае мы можем его использовать вместо одного из трех входных значений: , или . Почему «вместо«, а не «вместе«? Потому что для построения конуса достаточно трех параметров, а значение четвертого вычисляется через значения трех остальных.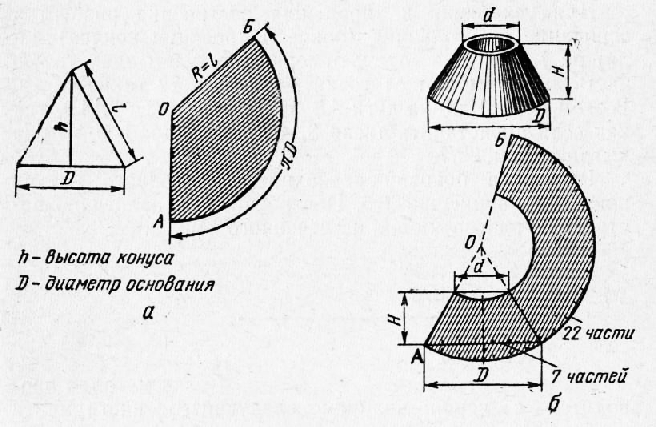 Почему именно трех, а не двух и не четырех — вопрос, выходящий за рамки этой статьи. Таинственный голос мне подсказывает, что это как-то связано с трехмерностью объекта «конус». (Сравните с двумя исходными параметрами двухмерного объекта «сегмент круга», по которым мы вычисляли все остальные его параметры в статье Геометрия круга.)
Почему именно трех, а не двух и не четырех — вопрос, выходящий за рамки этой статьи. Таинственный голос мне подсказывает, что это как-то связано с трехмерностью объекта «конус». (Сравните с двумя исходными параметрами двухмерного объекта «сегмент круга», по которым мы вычисляли все остальные его параметры в статье Геометрия круга.)
Ниже приведены формулы, по которым определяется четвертый параметр конуса, когда заданы три.
- Заданы ; тогда .
- Заданы ; тогда .
- Заданы ; тогда .
- Заданы ; тогда .
4. Методы построения выкройки
- Вычислить значения на калькуляторе и построить выкройку на бумаге (или сразу на металле) при помощи циркуля, линейки и транспортира.
- Занести формулы и исходные данные в электронную таблицу (например, Microsoft Exel). Полученный результат использовать для построения выкройки при помощи графического редактора (например, CorelDRAW).
- использовать мою программу Cones, которая нарисует на экране и выведет на печать выкройку для конуса с заданными параметрами.
 Эту выкройку можно сохранить в виде векторного файла и импортировать в CorelDRAW.
Эту выкройку можно сохранить в виде векторного файла и импортировать в CorelDRAW.
5. Не параллельные основания
Что касается усеченных конусов, то программа Cones пока строит выкройки для конусов, имеющих только параллельные основания.
Для тех, кто ищет способ построения выкройки усеченного конуса с не параллельными основаниями, привожу ссылку, предоставленную одним из посетителей сайта:
Усеченный конус с не параллельными основаниями.
геометрические формулы
прямой, наклонный и усеченный конус
Развертка поверхности конуса — это плоская фигура, полученная путем совмещения боковой поверхности и основания конуса с некоторой плоскостью.
Варианты построения развертки:
- Прямой круговой конус
- Наклонный конус
- Усеченный конус
Развертка прямого кругового конуса
Развертка боковой поверхности прямого кругового конуса представляет собой круговой сектор, радиус которого равен длине образующей конической поверхности l, а центральный угол φ определяется по формуле φ=360*R/l, где R – радиус окружности основания конуса.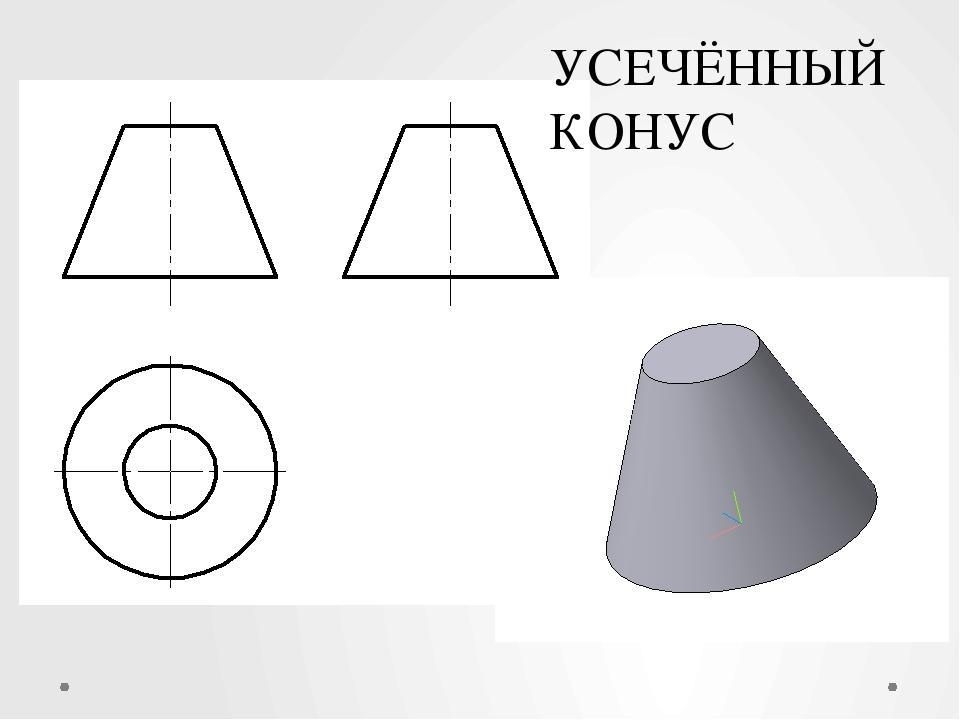
В ряде задач начертательной геометрии предпочтительным решением является аппроксимация (замена) конуса вписанной в него пирамидой и построение приближенной развертки, на которую удобно наносить линии, лежащие на конической поверхности.
Алгоритм построения
- Вписываем в коническую поверхность многоугольную пирамиду. Чем больше боковых граней у вписанной пирамиды, тем точнее соответствие между действительной и приближенной разверткой.
- Строим развертку боковой поверхности пирамиды способом треугольников. Точки, принадлежащие основанию конуса, соединяем плавной кривой.
Пример
На рисунке ниже в прямой круговой конус вписана правильная шестиугольная пирамида SABCDEF, и приближенная развертка его боковой поверхности состоит из шести равнобедренных треугольников – граней пирамиды.
Рассмотрим треугольник S0A0B0. Длины его сторон S0A0 и S0B0 равны образующей l конической поверхности. Величина A0B0 соответствует длине A’B’. Для построения треугольника S0A0B0 в произвольном месте чертежа откладываем отрезок S0A0=l, после чего из точек S0 и A0 проводим окружности радиусом S0B0=l и A0B0= A’B’ соответственно. Соединяем точку пересечения окружностей B0 с точками A0 и S0.
Величина A0B0 соответствует длине A’B’. Для построения треугольника S0A0B0 в произвольном месте чертежа откладываем отрезок S0A0=l, после чего из точек S0 и A0 проводим окружности радиусом S0B0=l и A0B0= A’B’ соответственно. Соединяем точку пересечения окружностей B0 с точками A0 и S0.
Грани S0B0C0, S0C0D0, S0D0E0, S0E0F0, S0F0A0 пирамиды SABCDEF строим аналогично треугольнику S0A0B0.
Точки A, B, C, D, E и F, лежащие в основании конуса, соединяем плавной кривой – дугой окружности, радиус которой равен l.
Развертка наклонного конуса
Рассмотрим порядок построения развертки боковой поверхности наклонного конуса методом аппроксимации (приближения).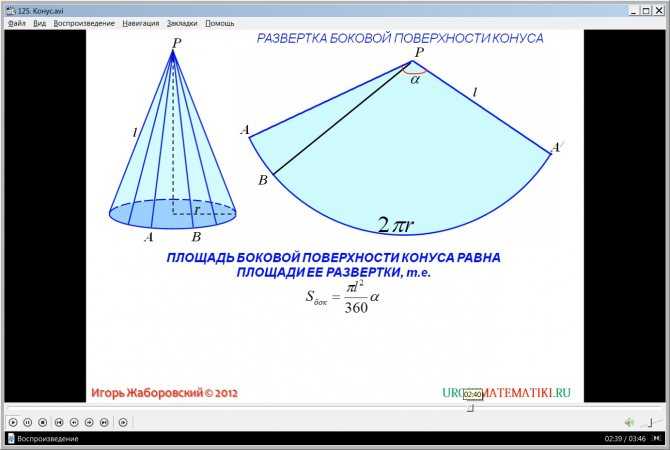
Алгоритм
- Вписываем в окружность основания конуса шестиугольник 123456. Соединяем точки 1, 2, 3, 4, 5 и 6 с вершиной S. Пирамида S123456, построенная таким образом, с некоторой степенью приближения является заменой конической поверхности и используется в этом качестве в дальнейших построениях.
- Определяем натуральные величины ребер пирамиды, используя способ вращения вокруг проецирующей прямой: в примере используется ось i, перпендикулярная горизонтальной плоскости проекций и проходящая через вершину S.
Так, в результате вращения ребра S5 его новая горизонтальная проекция S’5’1 занимает положение, при котором она параллельна фронтальной плоскости π2. Соответственно, S’’5’’1 – натуральная величина S5. - Строим развертку боковой поверхности пирамиды S123456, состоящую из шести треугольников: S01060, S06050, S05040, S04030, S03020, S02010.
 Построение каждого треугольника выполняется по трем сторонам. Например, у △S01060 длина S010=S’’1’’0, S060=S’’6’’1, 1060=1’6’.
Построение каждого треугольника выполняется по трем сторонам. Например, у △S01060 длина S010=S’’1’’0, S060=S’’6’’1, 1060=1’6’.
Степень соответствия приближенной развертки действительной зависит от количества граней вписанной пирамиды. Число граней выбирают, исходя из удобства чтения чертежа, требований к его точности, наличия характерных точек и линий, которые нужно перенести на развертку.
Перенос линии с поверхности конуса на развертку
Линия n, лежащая на поверхности конуса, образована в результате его пересечения с некоторой плоскостью (рисунок ниже). Рассмотрим алгоритм построения линии n на развертке.
Алгоритм
- Находим проекции точек A, B и C, в которых линия n пересекает ребра вписанной в конус пирамиды S123456.
- Определяем натуральную величину отрезков SA, SB, SC способом вращения вокруг проецирующей прямой.
 В рассматриваемом примере SA=S’’A’’, SB=S’’B’’1, SC=S’’C’’1.
В рассматриваемом примере SA=S’’A’’, SB=S’’B’’1, SC=S’’C’’1. - Находим положение точек A0, B0, C0 на соответствующих им ребрах пирамиды, откладывая на развертке отрезки S0A0=S’’A’’, S0B0=S’’B’’1, S0C0=S’’C’’1.
- Соединяем точки A0, B0, C0 плавной линией.
Развертка усеченного конуса
Описываемый ниже способ построения развертки прямого кругового усеченного конуса основан на принципе подобия.
Алгоритм
- Строим вспомогательный конус ε, подобный конусу ω, как это показано на рисунке выше. Для удобства построения величину диаметра d выбираем таким образом, чтобы соотношение t=D/d выражалось целым числом. В рассматриваемом примере t=2.
- Строим развертку боковой поверхности конуса ε – S0A01020304050A0 и на биссектрисе угла A0S0A0 отмечаем точку O0, выбрав ее расположение произвольно.

- Проводим прямые O0A0, O010, O020, O030, O040, O050, O0A0 и на них откладываем отрезки [O0A10]=t×|O0A0|, [O0110]= t×|O010|, [O0210]=t×|O020|, [O0310]=t×|O030|, [O0410]=t×|O040|, [O0510]=t×|O050|, [O0A10]=t×|O0A0| соответственно, где t=D/d. Соединяем точки A10, 110, 210, 310, 410, 510, A10 плавной линией.
- Из точек A10, 110, 210, 310, 410, 510, A10 проводим лучи, которые параллельны соответственно прямым A0S0, 10S0, 20S0, 30S0, 40S0, 50S0, A0S0, и на них откладываем отрезки A10B10, 110120, 210220, 310320, 410420, 510520, A10B10, равные l – образующей усеченного конуса.
 Проводим линию B10120220320420520B10.
Проводим линию B10120220320420520B10.
ПОДЕЛИТЬСЯ
Заказать чертеж
Вращающийся конус
Перейти к площади поверхности или объему.
Факты о конусе
Обратите внимание на эти интересные вещи:
- У него круг на одном конце
- И точка на другом конце
- И изогнутая сторона
- Это , а не многогранник.
имеет криволинейную поверхность
images/poly-gl.js?mode=cone
- Заостренный конец конуса называется вершиной
- Плоская часть является основанием
Объект в форме конуса называется коническим
изображения/cone-sweep.js
Конус представляет собой повернутый треугольник
Конус можно сделать, вращая треугольник!
Треугольник является прямоугольным, и он вращается вокруг одной из двух коротких сторон.
Сторона, вокруг которой он вращается, является осью конуса.
Правый против наклонного конуса
Когда вершина выровнена по центру основания, это прямой конус, в противном случае это наклонный конус:
Площадь поверхности конуса
Площадь поверхности состоит из двух частей:
- Базовая зона = π × r 2
- Боковая площадь = π × r × s
Что вместе составляет:
Площадь поверхности = π × r × (r + s)
Примечание: мы можем вычислить s = √(r 2 +h 2 )
Пример: h = 7 и r = 2
Площадь поверхности основания = π × r 2
= π × 2 2
= 4π
≈ 12,57
9000
Область поверхности поверхности. = π × r × √(r 2 +h 2 )
= π × 2 × √(2 2 +7 2 )
= π × 2 × √ (4 + 49)
= 2π√ (53)
≈ 45,74
Общая площадь поверхности ≈ 12,57 + 45,74 ≈ 58,31
7 + 45,74 ≈ 58,31
5.
Объем конуса
Объем =
1
3
π × г 2 × ч
Пример: h = 7 и r = 2
Объем=
1
3
π × r 2 × h
=
1
3
π × 2 2 × 7
=
28
3
π
≈ 29,32
Поиграй с этим здесь. Формула также работает, когда он «наклоняется» ( косой ), но помните, что высота всегда находится под прямым углом к основанию:
Объем конуса против цилиндра
Формулы объема для конусов и цилиндров очень похожи:
| Объем цилиндра: | π × г 2 × ч |
| Объем конуса: | 1 3 π × г 2 × ч |
Таким образом, объем конуса составляет ровно одну треть (
1
3
) объема цилиндра.
Мороженое нужно заказывать в цилиндрах, а не в рожках, получится в 3 раза больше!
Как пирамида
Конус также похож на пирамиду с бесконечным числом сторон, см. Пирамида против конуса.
Конусы различной формы
Строительный конус
Это почти конус, но вершина сколота (так называемый «усеченный конус»).
Также у него добавлено более широкое основание, чтобы он не упал!
873 874 875 876, 1833, 1834, 3399, 3400, 3401, 3402
Донные конусы бункера — Сбор урожая Ag
С нашими конусами нижнего бункера – больше не нужно перелопачивать зерно, больше не болит спина, больше не вдыхается пыль. Добавьте дополнительные бушели к существующему зерновому бункеру с быстрой и простой разгрузкой!
Наши конусы днища бункера доступны для новых или существующих зерновых бункеров.
- Конусы бункера окрашены внутри и снаружи. Конусы диаметром 12, 14 и 15 футов, как правило, состоят из одной детали, но могут быть легко собраны из двух частей, если возникают проблемы с транспортировкой
- Конусы диаметром 18–27 футов состоят из двух половин
- Стандартный наклон бункера: 12 футов – 45°, 14 футов и 15 футов – 40°, 18 футов и 21 фут – 38°, 24 дюйма и 27 футов – 35°
Наклон 45° доступен для всех конусов
См. таблицу ниже для получения дополнительной информации о наклонах конуса бункера и дополнительной вместимости бушелей
таблицу ниже для получения дополнительной информации о наклонах конуса бункера и дополнительной вместимости бушелей - Цельные конусы диаметром 18 и 21 фут доступны в качестве опции, если доставка осуществляется не слишком далеко от завода
Все бункеры стандартно поставляются с прочным люком с зубчатой рейкой и люком с крышкой. Конусы бункеров представляют собой цельнометаллическую конструкцию с квадратными трубчатыми ножками и распорками. Каждый конус бункера изготавливается на заказ для бункера, под который он будет устанавливаться, и будет работать с любым производителем зерновых бункеров.
Позвоните сегодня для бесплатной оценки и узнайте, какие другие варианты и нестандартные размеры доступны для экономии вашей рабочей силы и повышения производительности вашей работы.
Посмотреть фотогалерею нижних конусов бункера
Доступные варианты:
- Аэрация
- Прочный стальной кожух шнека с болтовым креплением (6 x 8 дюймов)
- Внешняя лестница
- Лестничная клетка
- Крышки нижнего пульта управления
- Шнеки для резервуаров для сыпучих материалов
- Стальная опора для конуса бункера
Преимущества и особенности:
- Больше не нужно копаться
- Нет больше вдыхания пыли
- Добавьте дополнительные бушели в существующий зерновой бункер
- Отличный вариант для непрерывной загрузки зерносушилки
- Быстрая и простая разгрузка – последний бушель выгрузить так же просто, как и первый
- Без шнека
- Превосходный семенной бункер – с бункерами проще работать с зерном, чем с уборщиками или пылесосами
- Доступ к люку в бункере для удобного доступа, обслуживания и очистки
| Размер бункера | Склон | Добавлены бушели | Высота конуса бункера |
|---|---|---|---|
| Диаметр 12 футов | 45 | 200 | 8′ |
| Диаметр 14 футов | 40 | 245 | 7 футов 10 дюймов |
| Диаметр 14 футов | 45 | 295 | 8 футов 9 дюймов |
| Диаметр 15 футов | 40 | 300 | 8’2″ |
| Диаметр 15 футов | 45 | 400 | 9 футов 11 дюймов |
| Диаметр 18 футов | 38 | 500 | 9 футов 3 дюйма |
| Диаметр 18 футов | 45 | 600 | 10 футов 11 дюймов |
| Диаметр 21 фут | 38 | 750 | 10 футов 2 дюйма |
| Диаметр 21 фут | 45 | 890 | 12 футов 8 дюймов |
| Диаметр 24 фута | 35 | 1 260 | 10 футов 9 дюймов |
| Диаметр 24 фута | 45 | 1 443 | 13 футов 9 дюймов |
| Диаметр 27 футов | 35 | 1 460 | 12 футов 3 дюйма |
| Диаметр 27 футов | 45 | 2 085 | 15 футов 6 дюймов |
Для получения дополнительной информации о наших конусах днища бункера или прицепах, пожалуйста, позвоните нам по телефону 620-345-8205 или напишите нам по электронной почте.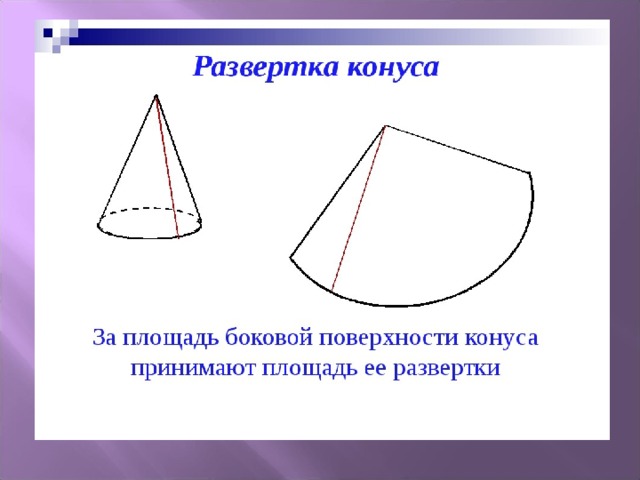
 Эту выкройку можно сохранить в виде векторного файла и импортировать в CorelDRAW.
Эту выкройку можно сохранить в виде векторного файла и импортировать в CorelDRAW. Построение каждого треугольника выполняется по трем сторонам. Например, у △S01060 длина S010=S’’1’’0, S060=S’’6’’1, 1060=1’6’.
Построение каждого треугольника выполняется по трем сторонам. Например, у △S01060 длина S010=S’’1’’0, S060=S’’6’’1, 1060=1’6’.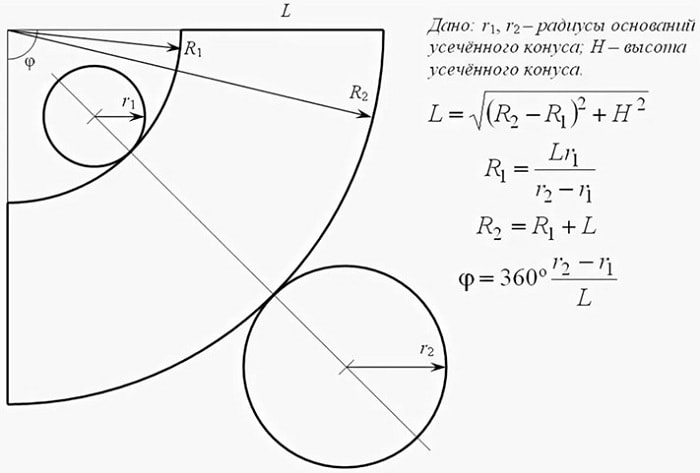 В рассматриваемом примере SA=S’’A’’, SB=S’’B’’1, SC=S’’C’’1.
В рассматриваемом примере SA=S’’A’’, SB=S’’B’’1, SC=S’’C’’1.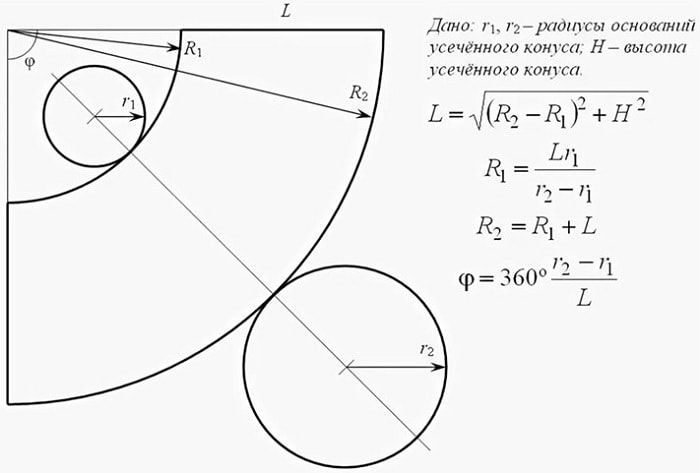
 Проводим линию B10120220320420520B10.
Проводим линию B10120220320420520B10.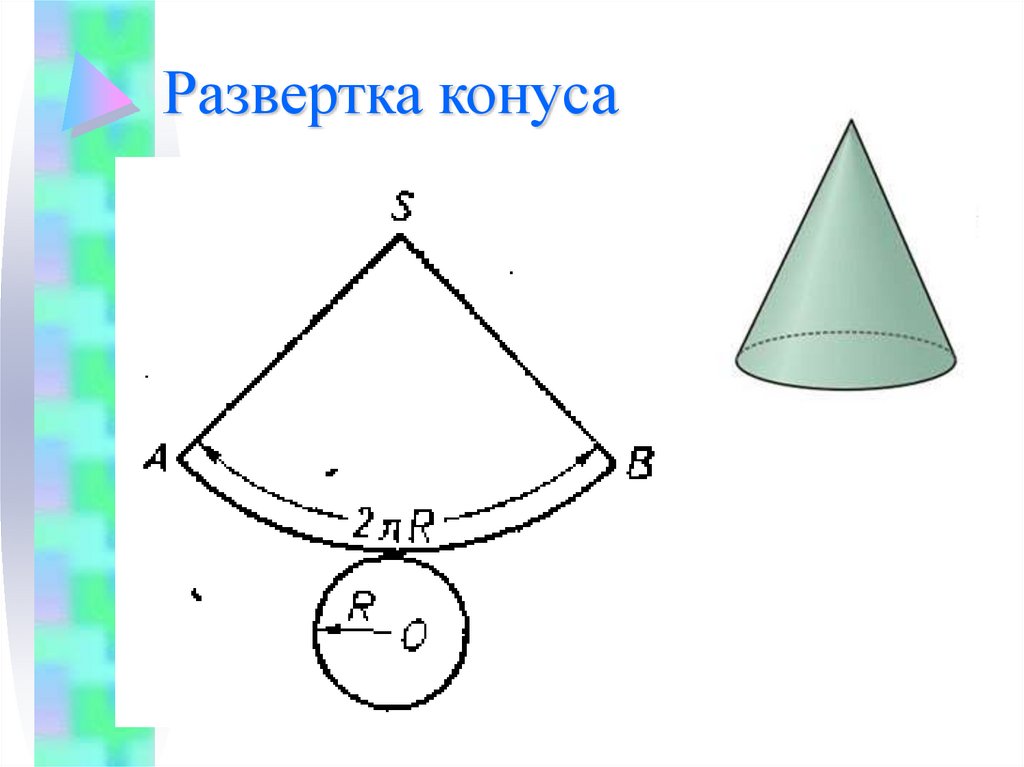 таблицу ниже для получения дополнительной информации о наклонах конуса бункера и дополнительной вместимости бушелей
таблицу ниже для получения дополнительной информации о наклонах конуса бункера и дополнительной вместимости бушелей