Развертка многогранника для склеивания. Развертка звездчатого многогранника

Много интересного можно найти для себя в тех сферах науки, которые, казалось бы, никогда не пригодятся в привычной жизни простого обывателя. Например, геометрия, о которой большинство забывают, только лишь переступив порог школы. Но странным образом малознакомые области науки становятся очень увлекательными, если с ними столкнуться поближе. Вот и геометрическая развертка многогранника – совершенно ненужная в повседневной жизни вещь – может стать началом увлекательного творчества, способного захватить и детей, и взрослых.

Красивая геометрия

Украшать интерьер дома, создавая своими руками необычные, стильные вещи, – это увлекательное творчество. Смастерить самостоятельно из плотной бумаги различные многогранники – значит создать уникальные вещи, которые могут стать просто занятием на день или два, а могут превратиться в дизайнерские интерьерные украшения. К тому же с развитием техники, способной к пространственному моделированию всевозможных вещей, стало возможным создание стильных и современных 3D-моделей. Есть мастера, которые при помощи простроения разверток по законам геометрии делают из бумаги макеты животных и различных предметов. Но это достаточно сложное математическое и чертежное творчество. Начать работать в подобной технике поможет развертка многогранника.

Разные грани — разные формы

Многогранники – это особая сфера геометрии. Они бывают простые – к примеру кубики, которыми дети играют с раннего возраста, – а бывают очень и очень сложные. Простроение развертки многогранников для склеивания считается достаточно сложной областью конструирования и творчества: нужно не только знать основы черчения, геометрические особенности пространства, но и иметь пространственное воображение, позволяющее оценить правильность решения еще на стадии проектирования. Но и одной фантазией не обойтись. Чтобы сделать развертки многогранников из бумаги, не достаточно просто представить, как в конце концов должна выглядеть работа. Нужно уметь правильно ее просчитать, сконструировать, а также грамотно начертить.

Самый первый многогранник – кубик

Скорее всего, каждый человек, посещавший школу, еще в начальных классах сталкивался на уроках труда с работой, результатом которой должен был стать бумажный кубик. Чаще всего учительница раздавала заготовки – развертки многогранника куба на плотной бумаге со специальными кармашками, предназначенными для склеивания граней модели в единое целое. Такой работой ученики начальной школы могли гордиться, ведь при помощи бумаги, ножниц, клея и своих усилий получалась интересная поделка – трехмерный куб.

Занимательные грани

Удивительно, но многие знания об окружающем мире становятся интересны не на школьной скамье, а лишь тогда, когда можно найти в них нечто увлекательное, способное дать что-то новое, необычное в привычной жизни. Не многие взрослые помнят, что те же многогранники делятся на огромное количество видов и подвидов. Например, есть так называемые платоновы тела – выпуклые многогранники, состоящие только лишь из правильных многоугольников. Таких тел всего пять: тетраэдр, октаэдр, гексаэдр (куб), икосаэдр, додекаэдр. Они представляют собой выпуклые фигуры без впадин. Звездчатые многогранники состоят из этих основных фигур в различных конфигурациях. Поэтому-то развертка многогранника простого позволяет нарисовать, вернее начерить, а затем и склеить из бумаги звездчатый многогранник.

Правильные и неправильные звездчатые многогранники

Складывая платоновые тела между собой в определенном порядке, вы можете построить немало звездчатых многоранников – красивых, сложных, многокомпонентных. Но они будут называться «неправильными звездчатыми многогранниками». Правильных звездчатых многогранников всего четыре: малый звездчатый додекаэдр, большой звездчатый додекаэдр, большой додекаэдр и большой икосаэдр. Развертки многогранников для склеивания не будут простыми чертежами. Они, как и фигуры, будут состоять из нескольких компонентов. Так, например, малый звездчатый додекаэдр строится из 12 пятиугольных равнобочных пирамид, сложенных по типу правильного додекаэдра. То есть для начала придется начертить и склеить 12 одинаковых штук правильных пирамид, состоящих из 5 равных граней. И только затем из них можно сложить звездчатый многогранник. Развертка самого малого звездчатого додекаэра – сложное и практически невыполнимое задание. Чтобы ее простроить, нужно суметь на одной плоскости уместить соединенные друг с другом 13 разверток разных геометрических объемных тел.

Красота в простоте

Все объемные тела, построенные по законам геометрии, будут смотреться завораживающе, в том числе и звездчатый многогранник. Развертка каждого элемента любого подобного тела должна быть выполнена максимально точно. И даже самые простые объемные многогранники, начиная с платонового тетраэдра, – удивительная красота гармонии мироздания и труда человека, воплощенного в бумажной модели. Вот, допустим, самый многогранный из платоновых выпуклых многогранников – додекаэдр. В этой геометрической фигуре 12 абсолютно одинаковых граней, 30 ребер и 12 вершин.Чтобы сделать развертки правильных многогранников для склеивания, нужно приложить максимум аккуратности и внимательности. И чем крупнее фигура по размерам, тем точнее должны быть все измерения.

Как построить развертку самостоятельно?

Пожалуй, помимо склеивания многогранника – хоть звездчатого, хоть платоновского, – еще интереснее построить развертку будущей модели собственными силами, оценив свои способности к черчению, конструированию и пространственному вообжению. Простые платоновсткие тела состоят из простых многоугольников, которые в одной фигуре идентичны друг другу. Так, тетраэдр – это три равнобедренных треугольника. Прежде чем простроить развертку, нужно представить себе, как правильно сложить плоские многоугольники между собой, чтобы получить многогранник. Треугольники можно соединить между собой по ребрам, прочертив один рядом с другим. Для склеивания развертки многогранников схемы должны быть снабжены специальными кармашками или клапанами, которые позволят соединить все части в единое целое. Тетраэдр – простейшая фигура из четырех граней. Октаэдр можно представить как двойной тетраэдр, у него восемь гарней – равнобедренных треугольников. Гексаэдром называют знакомый всем с детства куб. Икосаэдр представляет собой соединение 20 равнобедренных треугольников в правильный выпуклый многогранник. Додекаэдр – это объемная фигура из 12 граней, каждая из которых представляет собой правильный пятиугольник.

Тонкости работы

Построить разверту многогранника и склеить из нее бумажную модель – дело тонкое. Развертку, конечно, можно взять уже готовую. А можно, приложив услилия, построить ее самостоятельно. Но чтобы сделать полноценную объемную модель многогранника, нужно ее собрать. Многогранник лучше всего делать из плотной бумаги, которая хорошо держит форму и не коробится от клея. Все линии, которые необходимо согнуть, лучше всего предварительно продавить, используя, например, непишущую шариковую ручку или обратную сторону лезвия ножа. Этот нюанс поможет сложить модель аккуратнее, с соблюдением размеров и направлений ребер.

Если сделать разные многогранники из цветной бумаги, то такие модели можно использовать в качестве декоративных элементов, украшающих помещение – детскую комнату, кабинет, гостиную. Кстати, многогранники можно назвать уникальной находкой декораторов. Современные материалы позволяют на основе геометрических фигур создавать оригинальные предметы интерьера.

Новый: Развёртка многогранника

Что такое развертка многогранника? Вы скажете — кусок картона, из которого можно свернуть данный многогранник. В этом есть правда, но это не вся правда. Оказывается, понятие развертки включает в себя больше, чем просто кусок картона. 

Какой многогранник можно свернуть из столь хорошо известного латинского креста? Конечно же, куб. Для этого надо покрасить ребра, как это сделала наша волшебная кисточка (ребра одинакового цвета склеиваются в многограннике друг с другом). 

На самом деле, конечно же, лучше было бы раскрашивать не ребра, а каждую пару точек в разные цвета. Это бы задало, как говорят в математике, условия склейки границ. 

После того как условия склейки границ заданы, ребра, проходящие внутри куска картона, определены однозначно по теореме А. Д. Александрова. 

Итак, из креста можно сложить куб. 

Но оказывается, что если условия склейки границ задать по-другому, то можно получить совсем даже не куб! 

Наша волшебная кисточка покрасила границы вот таким образом. Еще один ее взмах — и мы уже знаем, как определены ребра внутри куска картона. Если теперь, следуя нарисованным условиям склейки, сложить многогранник, то получим пирамиду! 

Не так давно было доказано, что по-разному задавая условия склейки границ латинского креста, из него можно сложить 5 различных типов выпуклых многогранников. 

Итак, как мы убедились, в понятие развертки входит не только кусок картона, но и условия склейки его границ. Если последнее не определено, то из одного и того же куска можно сложить разные выпуклые многогранники. 

РАЗВЁРТКИ КУБА

Почти каждый, кто пытается самостоятельно найти все развёртки куба
сталкивается с вопросом: все ли развёртки найдены? Дело в том, что куб очень симметричная фигура и на подсознательном уровне нам кажется, что и число развёрток куба должно быть каким-то «красивым», похожим на другие характеристики куба (напомним, что куб имеет 12 рёбер, 8 вершин, 6 граней и 4 диагонали). Как оказалось, куб имеет 11 развёрток. И когда мы находим 11-ю развёртку, кажется, что не все ещё развёртки найдены и самые сложные ещё скрыты от нас. 
 Куб имеет именно 11 развёрток. 

РАЗВЁРТКА ПИРАМИДЫ

Сделать пирамиду из бумаги очень легко,  потому что я представлю вам готовую развертку, вам только нужно будет перенести ее на ваш лист, вырезать и склеить. Но, есть одно Большое И Положительное Но, если у вас есть принтер, тогда Вы сделаете пирамиду как минимум в два раза быстрее. Если он у вас есть, тогда надо только распечатать развертку на принтере, вырезать и  склеить – Все, пирамида готова! На этом все. Пользуйтесь на здоровье, делайте свою жизнь проше и получайте в школе за геометрические финуры только пятеркИ, ну или хотя бы четверки! Удачи!

Посмотрите интересные развёртки

Многогранники в программе Poly

СОЗДАНИЕ РАЗВЁРТКИ — ИНТЕРЕСНОЕ И УВЛЕКАТЕЛЬНОЕ ДЕЛО.

Существование многогранника с заданной разверткой

Существование многогранника с заданной разверткой

Скачать PDF

• Опубликовано: 11 ноября 2020 г.

• Ю. Волков А. ¹  

Журнал математических наук
том 251 , страницы 462–479 (2020)Процитировать эту статью

• 35 доступов

• Сведения о показателях

Настоящая статья является публикацией кандидатской диссертации Юрия Александровича Волкова (1930–1981).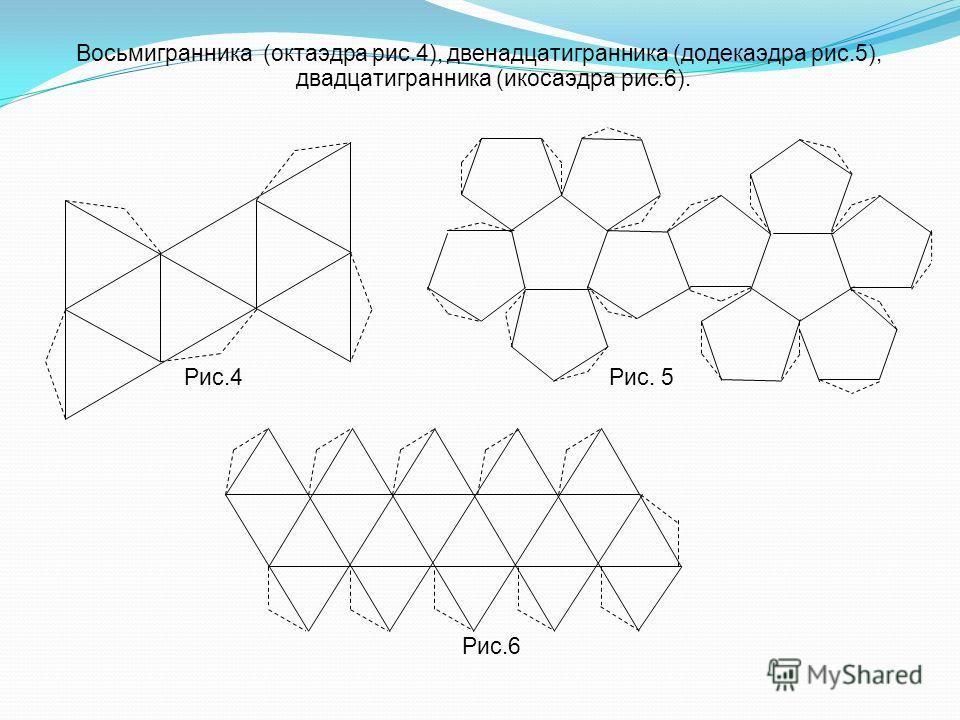 кандидатскую диссертацию, в которой вариационным методом доказана знаменитая теорема А.Д. Александрова о существовании выпуклого многогранника с заданной разверткой.

Скачайте, чтобы прочитать полный текст статьи

Литература

1. Александров А.Д., Выпуклые многогранники , Гос. Издат. Техн.-теор. лит., Москва–Ленинград (1950).

2. А. Д. Александров, Die innere Geometrie der konvexen Flächen , Akademie-Verlag, Berlin (1955).

   Google ученый

3. Ефимов Н. В. Качественные вопросы теории деформации поверхностей // УМН. ( Н.С. ), 3 , № 2(24), 47–158 (1948).

   MathSciNet
   МАТЕМАТИКА

   Google ученый

4. В. Блашке, Г. Херглотц, «¨Über die Verwirklichung einer geschlossenen Fläche mit vorgeschriebenem Bogenelement im Euklidischen Raum», Sitzungsber. Байер. акад. Висс. , 2 , 229–230 (1937).

   МАТЕМАТИКА

   Google ученый

5. А. В. Погорелов, Деформация выпуклых поверхностей , Гос. Издат. Техн.-теор. лит., Москва–Ленинград (1951).

Скачать ссылки

Информация об авторе

Авторы и организации

1. Санкт-Петербургский государственный университет, Санкт-Петербург, Россия

   Ю.А. А. Волков

Авторы

1. Ю.А. А. Волков

   Посмотреть публикации автора

   Вы также можете искать этого автора в
   PubMed Google Scholar

Дополнительная информация

Перевод с Записки научных семинаров ПОМИ , Том. 476, 2018, стр. 50–78.

Права и разрешения

Перепечатка и разрешения

Об этой статье

Polyhedron Graph — GeeksforGeeks

Слово «многогранник» состоит из двух греческих слов: первое — «поли», что означает «много», а второе — «эдр», что означает поверхность. Как правило, любая твердая форма с плоскими гранями и прямыми ребрами называется многогранником. Поскольку имя включает в себя «поли» в качестве префикса, имя формы зависит от количества граней, присутствующих в конкретной форме. Например, многогранник с четырьмя гранями известен как 9.0123 Тетраэдр .

Введение в многогранный граф:

Многогранный граф — это сеть, соединяющая различные концепции или переменные. В многогранном графе каждая вершина имеет n ребер. Многогранные графы — это неориентированные графы, ребра и вершины которых образуют выпуклые многогранники. Многогранные графы, с другой стороны, являются чисто теоретико-графовыми связными графами с 3 вершинами. Обратитесь к приложенному рисунку для лучшего понимания.

Многогранный граф

Характеристики многогранного графа:

Многогранник обладает следующими свойствами:

• Гранями многогранника являются плоские поверхности, составляющие многогранник. Это обычные многоугольные грани.
• Ребра — это места, где две плоские поверхности встречаются, образуя линейный сегмент.
• Вершина — это точка, в которой пересекаются ребра многогранника. Вершина также известна как угол многогранника.
• Многогранный граф — это граф, созданный из вершин и ребер выпуклого многогранника.
• Каждый многогранник удовлетворяет формуле Эйлера или формуле многогранника.

 F + V = E + 2,  (здесь F относится к граням, V относится к вершинам, а E относится к ребрам)

Части многогранника

может быть дополнительно классифицирован на основе элементов, которые его образуют (вершины, грани и ребра), в следующие подкатегории.

• Правильный многогранник
• Неправильный многогранник

Диаграммы см. на изображениях.

Типы многогранников

Правильный многогранник: Правильный многогранник состоит из правильных многоугольников, расположенных в правильном порядке. Термин «платоническое твердое тело» также используется для описания таких твердых тел. Эти многогранники конгруэнтны по своей природе. Другими словами, мы можем сказать, что множество многоугольников, объединенных вместе, чтобы сформировать правильный многогранник, конгруэнтно друг другу. Обратитесь к приложенному рисунку для лучшего понимания.

Правильный многогранник

Неправильный многогранник: Неправильный многогранник образован многоугольниками неидентичной формы, и эти многоугольники составляют многогранник асимметричной формы. Существует разница в размерах между многогранниками с неправильными гранями и многогранниками с правильными гранями. Другими словами, сочетание разных типов многоугольников вместе образует неправильный многогранник. Обратитесь к приложенному рисунку для лучшего понимания.

Неправильный многогранник

Двойной многогранник:

Как говорит само значение, многогранник происходит из другой структуры в ассоциации.