Развертка Призмы Для Склеивания. Развертка наклонной призмы для склеивания
Развертка многогранника для склеивания. Развертка звездчатого многогранника
Много интересного можно найти для себя в тех сферах науки, которые, казалось бы, никогда не пригодятся в привычной жизни простого обывателя. Например, геометрия, о которой большинство забывают, только лишь переступив порог школы. Но странным образом малознакомые области науки становятся очень увлекательными, если с ними столкнуться поближе. Вот и геометрическая развертка многогранника – совершенно ненужная в повседневной жизни вещь – может стать началом увлекательного творчества, способного захватить и детей, и взрослых.
Красивая геометрия
Украшать интерьер дома, создавая своими руками необычные, стильные вещи, – это увлекательное творчество. Смастерить самостоятельно из плотной бумаги различные многогранники – значит создать уникальные вещи, которые могут стать просто занятием на день или два, а могут превратиться в дизайнерские интерьерные украшения. К тому же с развитием техники, способной к пространственному моделированию всевозможных вещей, стало возможным создание стильных и современных 3D-моделей. Есть мастера, которые при помощи простроения разверток по законам геометрии делают из бумаги макеты животных и различных предметов. Но это достаточно сложное математическое и чертежное творчество. Начать работать в подобной технике поможет развертка многогранника.
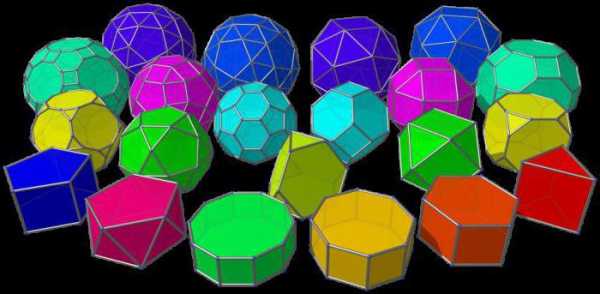
Разные грани - разные формы
Многогранники – это особая сфера геометрии. Они бывают простые – к примеру кубики, которыми дети играют с раннего возраста, – а бывают очень и очень сложные. Простроение развертки многогранников для склеивания считается достаточно сложной областью конструирования и творчества: нужно не только знать основы черчения, геометрические особенности пространства, но и иметь пространственное воображение, позволяющее оценить правильность решения еще на стадии проектирования. Но и одной фантазией не обойтись. Чтобы сделать развертки многогранников из бумаги, не достаточно просто представить, как в конце концов должна выглядеть работа. Нужно уметь правильно ее просчитать, сконструировать, а также грамотно начертить.

Самый первый многогранник – кубик
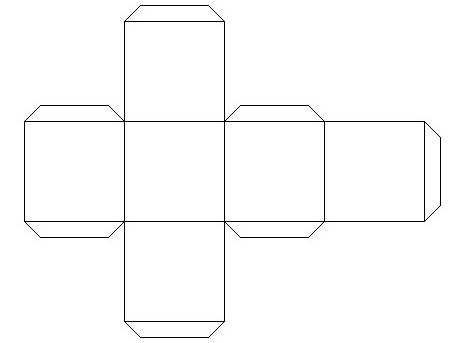
Скорее всего, каждый человек, посещавший школу, еще в начальных классах сталкивался на уроках труда с работой, результатом которой должен был стать бумажный кубик. Чаще всего учительница раздавала заготовки – развертки многогранника куба на плотной бумаге со специальными кармашками, предназначенными для склеивания граней модели в единое целое. Такой работой ученики начальной школы могли гордиться, ведь при помощи бумаги, ножниц, клея и своих усилий получалась интересная поделка – трехмерный куб.
Занимательные грани
Удивительно, но многие знания об окружающем мире становятся интересны не на школьной скамье, а лишь тогда, когда можно найти в них нечто увлекательное, способное дать что-то новое, необычное в привычной жизни. Не многие взрослые помнят, что те же многогранники делятся на огромное количество видов и подвидов. Например, есть так называемые платоновы тела – выпуклые многогранники, состоящие только лишь из правильных многоугольников. Таких тел всего пять: тетраэдр, октаэдр, гексаэдр (куб), икосаэдр, додекаэдр. Они представляют собой выпуклые фигуры без впадин. Звездчатые многогранники состоят из этих основных фигур в различных конфигурациях. Поэтому-то развертка многогранника простого позволяет нарисовать, вернее начерить, а затем и склеить из бумаги звездчатый многогранник.
Правильные и неправильные звездчатые многогранники
Складывая платоновые тела между собой в определенном порядке, вы можете построить немало звездчатых многоранников – красивых, сложных, многокомпонентных. Но они будут называться "неправильными звездчатыми многогранниками". Правильных звездчатых многогранников всего четыре: малый звездчатый додекаэдр, большой звездчатый додекаэдр, большой додекаэдр и большой икосаэдр. Развертки многогранников для склеивания не будут простыми чертежами. Они, как и фигуры, будут состоять из нескольких компонентов. Так, например, малый звездчатый додекаэдр строится из 12 пятиугольных равнобочных пирамид, сложенных по типу правильного додекаэдра. То есть для начала придется начертить и склеить 12 одинаковых штук правильных пирамид, состоящих из 5 равных граней. И только затем из них можно сложить звездчатый многогранник. Развертка самого малого звездчатого додекаэра – сложное и практически невыполнимое задание. Чтобы ее простроить, нужно суметь на одной плоскости уместить соединенные друг с другом 13 разверток разных геометрических объемных тел.
Красота в простоте
Все объемные тела, построенные по законам геометрии, будут смотреться завораживающе, в том числе и звездчатый многогранник. Развертка каждого элемента любого подобного тела должна быть выполнена максимально точно. И даже самые простые объемные многогранники, начиная с платонового тетраэдра, – удивительная красота гармонии мироздания и труда человека, воплощенного в бумажной модели. Вот, допустим, самый многогранный из платоновых выпуклых многогранников – додекаэдр. В этой геометрической фигуре 12 абсолютно одинаковых граней, 30 ребер и 12 вершин.Чтобы сделать развертки правильных многогранников для склеивания, нужно приложить максимум аккуратности и внимательности. И чем крупнее фигура по размерам, тем точнее должны быть все измерения.
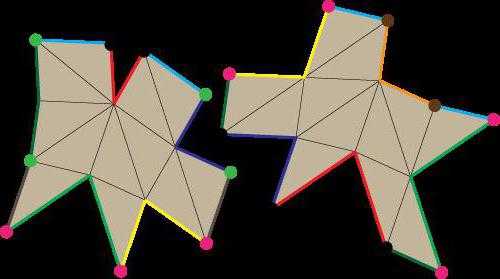
Как построить развертку самостоятельно?
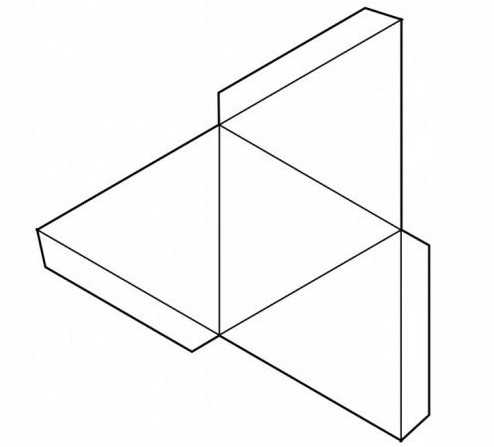
Пожалуй, помимо склеивания многогранника – хоть звездчатого, хоть платоновского, – еще интереснее построить развертку будущей модели собственными силами, оценив свои способности к черчению, конструированию и пространственному вообжению. Простые платоновсткие тела состоят из простых многоугольников, которые в одной фигуре идентичны друг другу. Так, тетраэдр – это три равнобедренных треугольника. Прежде чем простроить развертку, нужно представить себе, как правильно сложить плоские многоугольники между собой, чтобы получить многогранник. Треугольники можно соединить между собой по ребрам, прочертив один рядом с другим. Для склеивания развертки многогранников схемы должны быть снабжены специальными кармашками или клапанами, которые позволят соединить все части в единое целое. Тетраэдр – простейшая фигура из четырех граней. Октаэдр можно представить как двойной тетраэдр, у него восемь гарней – равнобедренных треугольников. Гексаэдром называют знакомый всем с детства куб. Икосаэдр представляет собой соединение 20 равнобедренных треугольников в правильный выпуклый многогранник. Додекаэдр – это объемная фигура из 12 граней, каждая из которых представляет собой правильный пятиугольник.
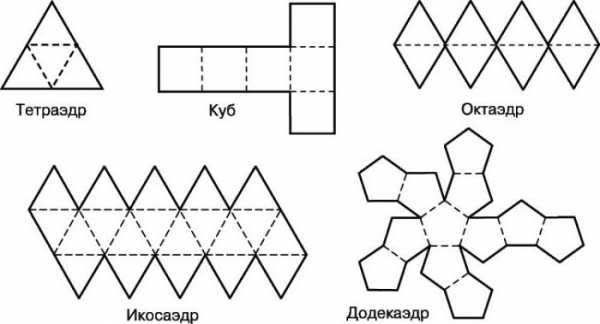
Тонкости работы
Построить разверту многогранника и склеить из нее бумажную модель – дело тонкое. Развертку, конечно, можно взять уже готовую. А можно, приложив услилия, построить ее самостоятельно. Но чтобы сделать полноценную объемную модель многогранника, нужно ее собрать. Многогранник лучше всего делать из плотной бумаги, которая хорошо держит форму и не коробится от клея. Все линии, которые необходимо согнуть, лучше всего предварительно продавить, используя, например, непишущую шариковую ручку или обратную сторону лезвия ножа. Этот нюанс поможет сложить модель аккуратнее, с соблюдением размеров и направлений ребер.

Если сделать разные многогранники из цветной бумаги, то такие модели можно использовать в качестве декоративных элементов, украшающих помещение – детскую комнату, кабинет, гостиную. Кстати, многогранники можно назвать уникальной находкой декораторов. Современные материалы позволяют на основе геометрических фигур создавать оригинальные предметы интерьера.
fb.ru
Развертка поверхности призмы
Существует два способа развертки призмы: способ «нормального сечения» и способ «раскатки».
Способ «нормального сечения» используют для развертки поверхности призм общего положения. В этом случае строится нормальное сечение призмы (т.е. вводится плоскость, расположенная перпендикулярно боковым ребрам призмы) и определяются натуральные величины сторон многоугольника этого нормального сечения.
Пример выполнения развертки трехгранной призмы общего положения способом «нормального сечения» рассмотрим в задаче согласно рисунка 1.5.1
Обратим внимание на то, что в нашем случае боковые ребра призмы являются фронталями, т.е. на плоскость П2они проецируются в натуральную величину.
Решение:
1) Во фронтальной плоскости проекций построим фронтально проецирующую плоскость γ(γ1), которая одновременно перпендикулярна боковым ребрам призмы AD, CF, BE. Полученное нормальное сечение выразится в виде треугольника 123. Методом плоско-параллельного перемещения определим его натуральную величину в соответствии с рисунком 1.5.2.
2) Все стороны нормального сечения последовательно отложим на прямой: 1020=111211; 2030=211311; 3010=311111.
3) Через точки 10,20,30 проведем прямые, перпендикулярные прямой 10-10и отложим на них натуральную величину боковых ребер: 10D0 =12D2и 10A0 = 12A2; 20F0 = 22F2и 20C0 = 22C2; 30E0 = 32E2и 30B0 = 32B2.
4) Полученные точки верхнего и нижнего оснований призмы соединим прямыми A0B0C0и D0F0E0. Плоская фигура A0B0C0D0F0E0 является искомой разверткой боковой поверхности данной призмы. Для построения полной развертки необходимо к развертке боковой поверхности пристроить натуральные величины оснований. Для этого воспользуемся полученными на развертке натуральными величинами их сторон A0C0, C0B0, B0A0и D0F0, F0E0, E0D0 в соответствии с рисунком 1.5.3
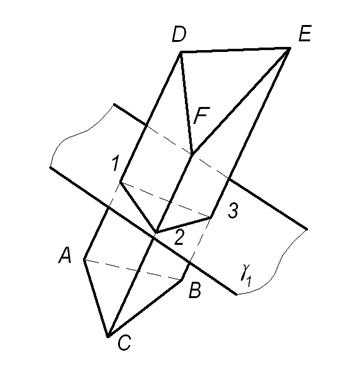
Рисунок 1.5.1
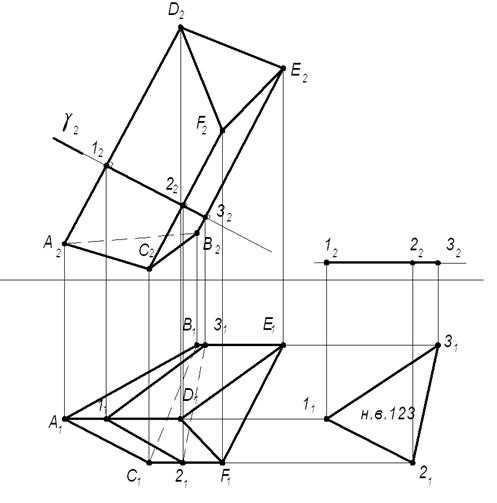
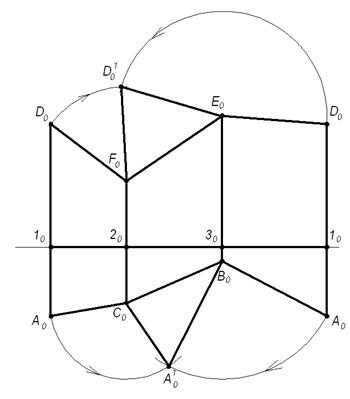
Рисунок 1.5.3 – Развертка призмы способом «нормального сечения»
Способ «раскатки». Этот способ удобен для построения разверток призм с основанием, лежащим в плоскости уровня. Суть способа заключается в последовательном совмещением боковых граней с плоскостью чертежа путем поворота их вокруг соответствующих ребер призмы (рисунок 1.5.4).
Этим способом построена развертка поверхности призмы ABCDEF , боковые ребра которой являются фронталями, а нижнее основание лежит в горизонтальной плоскости (рисунок 1.5.5).
Решение:
1) Боковые грани призмы совместим с фронтальной плоскостью, проходящей через ребро AD. Это удобно в этом случае, т.к. фронтальные проекции боковых ребер призмы равны их истинной длине. Тогда ребро A0D0 развертки будет совпадать с фронтальной проекцией ребра AD(A2D2).
2) Для определения на развертке истиной величины боковой грани ADEB вращаем ее вокруг ребра AD до положения, параллельного фронтальной плоскости проекций. Чтобы определить на развертке положение точки B0, из точки B2 восстанавливаем перпендикуляр к A2D2. Точка B0 будет найдена в пересечении этого перпендикуляра с дугой окружности радиуса R1, равного истиной величине ребра AB и проведенной из точки A2, как из центра.
3) Точка E0 будет определяться на развертке как результат пересечения прямой B0E0 параллельной фронтальной проекцией ребра BE(B2E2), и перпендикуляра, восстановленного из точки E2к A2D2.
4) Точки C0 и A0 построены аналогично точке B0в пересечении перпендикуляров из точек C2и A2 к фронтальным проекциям ребер, с дугами окружностей, проведенных из точек B0и C0 как из центров радиусами R2 и R3, равными соответственно ребрам BC и CA. Точки F0и D0 определяются аналогично точке E0.
5) Соединив последовательно совмещенные вершины ломаными линиями, получим развертку боковой поверхности призмы A0B0C0A0D0F0E0D0. При необходимости можно получить полную развертку призмы, присоединив к ней натуральные величины обоих оснований.
Если боковые ребра призмы занимают общее положение, то предварительным преобразованием чертежа их надо привести в положение линий уровня.
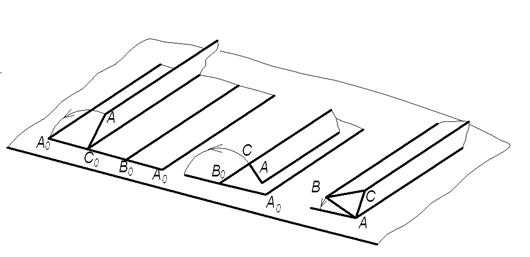
Рисунок 1.5.4 – Способ «раскатки»
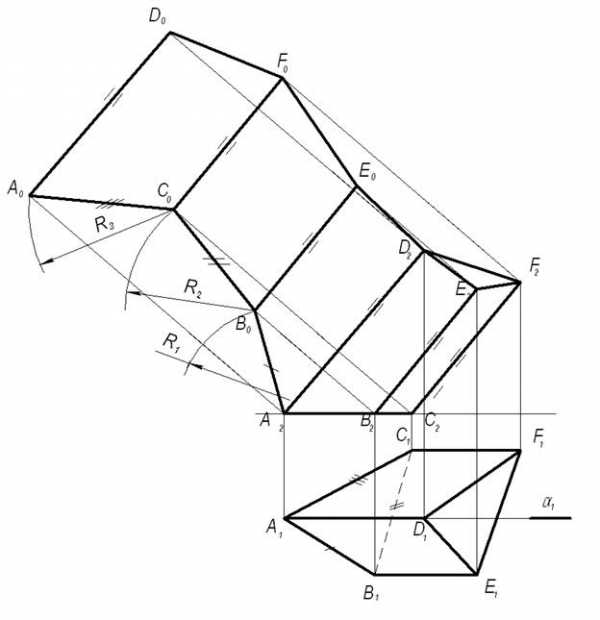
Рисунок 1.5.5 – Развертка боковой поверхности призмы способом «раскатки»
Похожие статьи:
poznayka.org
Как начертить в изометрии правильные треугольную призму и шестиугольную? Способ только один?
Треугольную строишь так. Основание - параллельно оси изометрии. Делишь эту сторону пополам, и через точку деления проводишь прямую, параллельную второй оси.. Считаешь длину высоты через сторону, с учетом коэффициента искажения: H=(a√3/2)×K Получаешь третью вершину, соединяешь ее с первыми двумя. Остальное - просто. С шестиугольником будет посложнее. Сторона - вдоль первой оси, малая диагональ - параллельно второй оси. В оригинале она перпендикулярна стороне. Считай ее длину через сторону: H=a√3.×К Построй эту диагональ, через ее свободную точку проведи прямую, параллельную первой оси. На этой прямой отложи отрезок, равный стороне. Теперь строишь прямую через середины получившихся сторон. Ее отрезок между сторонами делишь на 2 и проводишь прямую, параллельную двум построенным сторонам. На этой прямой от точки пересечения ее со средней линией, отложи вправо-влево по отрезку, равному стороне. Всё. Есть все шесть вершин.
1Начертите основания призмы, в данном случае это будут 2 шестиугольника. Для того, чтобы начертить правильный шестиугольник воспользуйтесь циркулем. Нарисуйте им круг, и с помощью этого же радиуса разделите окружность на шесть частей (у правильного шестиугольника стороны равны радиусу описанной окружности). Получившаяся фигура напоминает ячейку пчелиной соты. Неправильный шестиугольник начертите произвольно, но с помощью линейки. 2.Теперь приступайте к проектированию «выкройки». Стенками призмы являются параллелограммы, и вам нужно их начертить. В прямой модели параллелограммом будет простой прямоугольник. И его ширина будет всегда равна стороне шестиугольника, лежащего в основании призмы. При правильной фигуре в основании, все грани призмы будут равны между собой. При неправильной – каждой стороне шестиугольника будет соответствовать только один параллелограмм (одна боковая грань), подходящий по размеру. При этом следите за последовательностью размеров граней. .3.На горизонтальной прямой последовательно отложите 6 отрезков, равных стороне основания шестиугольника. Из полученных точек проведите перпендикулярные линии нужной высоты. Концы перпендикуляров соедините второй горизонтальной линией. У вас получилось 6 прямоугольников, соединенных вместе. 4.Пристройте к нижней и верхней стороне одного из прямоугольников 2 сконструированных ранее шестиугольника. К любому основанию, если он правильный, и к соответствующему по длине, если шестиугольник неправильный. Обведите контур сплошной линией, а линии сгиба внутри фигуры – пунктирной. У вас получилась развертка поверхности прямой призмы. 5.Для создания наклонной призмы основания оставьте такими же. Начертите сторону-параллелограмм, которая будет являться одной из граней. Таких граней должно быть шесть, как вы помните. Чтобы теперь начертить развертку наклонной призмы, нужно расположить шесть параллелограммов в следующем порядке: три по возрастанию, так, чтобы их косые стороны образовали одну линию, далее три по убыванию с тем же условием. Крутизна получившейся линии прямо пропорциональна градусу наклона призмы. 6.К пяти прямоугольникам в развертке пририсуйте небольшие трапециевидные захлесты на коротких сторонах для склеивания фигуры, а также на одной свободной длинной стороне. Вырежете заготовку для призмы вместе с захлестами и склейте модель.
чертишь прямоугольник ставишь . в середине от неечертиш 4 линии в 4 угла
touch.otvet.mail.ru
Развертка Призмы Для Склеивания
Оптические призмы. Оптические призмы являются одним из основных элементов при создании оптических систем и оптических приборов.
Таблица - многогранники, которые можно изготовить своими руками из бумаги, даны ссылки на инструкции, схемы, развертки в различных источниках .
Призмы широко используются в оптических приборах различного назначения, таких как наблюдательные оптические приборы (телескопы, бинокли, микроскопы и другие), оптические приборы для регистрации изображений на электронных приёмниках, сложные многофункциональные оптические приборы. Причём, чем сложнее оптический прибор, тем большее количество и номенклатура оптических призм может в нём использоваться. Например, большое число сложных оптических призм используется в таких оптических приборах как спектральные оптические приборы, интерферометры, поляриметры и другие. Оптические призмы в зависимости от их оптической конструкции функционально позволяют: Изменять ход лучей в оптических приборах; Изменять направление оптической оси системы; Изменять направление линии оптического визирования; Оборачивать оптические изображения; Уменьшать габариты оптических систем; Разделять пучки лучей в оптических системах; Объединять поля в оптических системах; Вращать в оптических системах изображения; Компенсировать в оптических системах поворот изображения; Разлагать белый свет в спектр; Получать поляризованный свет; Следует отметить, что действие оптической призмы подобно зеркалу. Отметим некоторые преимущества призм перед зеркалами: Действие одной призмы, часто, заменяет действие системы зеркал. Углы между зеркалами должны регулироваться с большой точностью при сборке, система зеркал подвержена разъюстированию.
- Просто ввел 'треугольная призма', но не полез по ссылкам, а открыл 'Картинки'. Делается развёртка, вырезается, склеивается. Попробуйте дать поиск - развёртка.
- Правильная семигранная призма, развертка правильной семигранной призмы, правильная семиугольная призма, развертка правильной семиугольной .
- Развертка пирамиды для склеивания. Развертки из бумаги. Определение параметров. Прежде всего определим, какой будет пирамида. Развертка данной фигуры является основой для изготовления объемной фигуры.
- Нужно склеить несколько геометрических фигур? Скачайте развертки абсолютно бесплатно! Вся сложность склеивания конуса в его острой вершине, а потом ещё будет очень сложно приклеить дно.
Углы между гранями призмы неизменны; Потери света у призм от граней с полным внутренним отражением равны нулю, тогда как при отражении от поверхностей зеркал потери довольно велики; кроме того, отражающие покрытия зеркал с течением времени могут портиться; Конструкция крепления призм в оправах, как правило, проще чем системы зеркал, имеет меньшие габариты; Для некоторых призм нет эквивалентных зеркальных систем (например, призма Дове, полупента, некоторые виды спектральных призм). Вместе с тем, встречаются оптические системы и оптические приборы, в которых замена оптических призм на зеркала целесообразна. Важнейшими факторами являются вес прибора (зеркала значительно легче призм), а также стоимость. Кроме того призмы в ряде случаев являются источниками хроматических и некоторых других аберраций. Рабочие и нерабочие поверхности призмы - плоскости. Различают преломляющие рабочие поверхности призмы, через которые световой пучок входит в призму и выходит из нее, и отражающие поверхности призмы, от которых пучок отражается при прохождении внутри призмы. Число рабочих граней и взаимное их расположение определяет ход пучка внутри призмы и все преобразования пучка, которые при этом происходят.
Если осевой луч проходит внутри призмы в одной плоскости, то такую призму называют плоской. Если осевой луч идет в двух плоскостях, - такая призма называется пространственной. Сечение призмы плоскостью, в которой проходит осевой луч пучка, называется главным сечением призмы; у плоских призм одно главное сечение, у пространственных главных сечений столько, сколько плоскостей, в которых проходит осевой луч.
Чертежи разверток поверхностей призм и цилиндров. Для изготовления ограждений станков, вентиляционных труб и некоторых других изделий вырезают из листового материала их развертки. Развертка поверхностей любой прямой призмы представляет собой плоскую.
Отражательные призмы. Основными характеристиками работы отражательных призм являются угол отклонения и смещение светового пучка, а также оборачивание изображения. Углом отклонения называется угол между направлениями осевого луча до и после призмы, причем, промежуточные отклонения луча внутри призмы во внимание не принимаются. Оборачивание изображения зависит от числа отражающих граней и их расположения в пространстве. Для плоских призм при четном числе отражающих граней изображение не оборачивается призмой, при нечетном - оборачивается в главном сечении. Для оборачивания изображения в плоскости, нормальной к главному сечению, одна из отражающих граней призмы заменяется крышей, которая представляет собой две отражающих поверхности, образующие двугранный угол 9.
Первая буква указывает число отражающих граней призмы ( А - одно отражение, Б - два, В - три), вторая - характер ее конструкции (Р - равнобедренная, П - пента- призма, У - полупента, С - ромбическая, Л - призма Лемана). Число обозначает угол отклонения осевого луча в градусах. При этом крыша считается за одну грань.
Обозначается крыша индексом . Для пространственных призм указываются углы отклонения в соответствующих плоскостях по ходу луча. Плоские призмы с четным числом отражающих граней дают прямое изображение. При наклоне такой призмы в главной плоскости выходящий пучок лучей не отклоняется.
Плоские призмы с нечетным числом отражающих граней дают зеркальное изображение предмета. Бесплатные Программы Для Регистрации Договоров тут. При наклоне их в плоскости главного сечения лучи отклоняются на двойной угол. Отражательные призмы развертываются в плоскопараллельную пластинку.
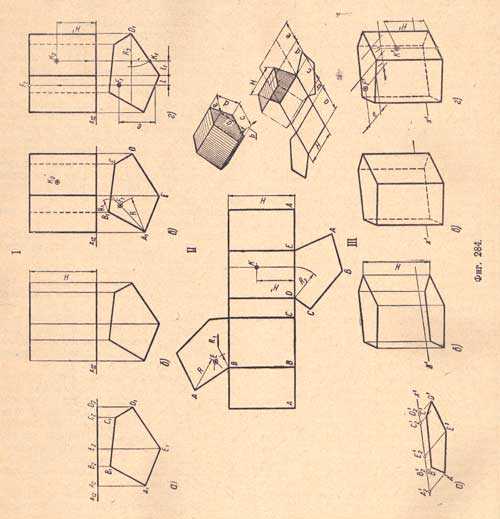
Развертка призмы выполняется путем постепенного перевертывания контура главного сечения призмы вокруг отражающих граней по ходу луча в призме. Длина развертки призмы равна геометрической длине хода пучка в призме (рис.
Если призма не развертывается в плоскопараллельную пластинку, то она действует как клин с большим преломляющим углом и вызывает хроматизм и искажение изображения. Такие призмы применяются с дополнительным (компенсирующим) клином. Призмы, представляющие собой комбинации из двух или большего числа простых типовых призм, скрепляемых в единый блок с помощью склейки или закрепления в оправе, называются составными или сложными. Они применяются в тех случаях, когда типовые призмы не подходят для проектируемой системы по габаритам или углу отклонения, или требуется уменьшить габариты системы. На рис. 4 а,б приведены призмы с клином, рис.
На рис. 5 а,б приведены составные пространственные призмы, использующиеся как оборачивающие призменные системы - призменные системы Малафеева- Порро первого и второго рода соответственно. Обычное назначение отражательных призм - отклонение пучка и оборачивание изображения.
Однако в оптических приборах часто применяются призмы, решающие и другие задачи, например, соединение или разделение пучков, разделение поля. Примеры призм, решающих подобные задачи, приведены на рис. Спектральные призмы. Спектральной призмой называется многогранник, сделанный из прозрачного вещества, обладающего значительной дисперсией (dn/d l ). Угол выхода лучей из призмы зависит от длины волны излучения. Прохождение луча через призму связано с преломлением, зависящим от материала. Для изготовления хороших спектральных призм должен использоваться материал, прозрачный с исследуемой области спектра, обладающий большой дисперсией, высокой оптической однородностью и изотропностью, быть сравнительно недорогим и хорошо обрабатываться.
Материал для поляризационных призм, напротив, должен быть анизотропным. Для ультрафиолетовой части спектра часто используется природный кристаллический кварц, хотя он обладает двойным лучепреломлением, вращает плоскость поляризации, достаточно дорог и недоступен в виде больших кусков достаточной однородности и прозрачности. Получаемый искусственным выращиванием кварц достаточно однороден и свободен от двойного лучепреломления. Однако для видимой области кварцевые призмы малопригодны. Для видимой области основным материалом для изготовления спектральных призм служит стекло.
Как правило, спектральные призмы делают из тяжелых стекол типа флинт, обладающих большой дисперсией. Для большинства сортов тяжелых стекол большая дисперсия сопровождается значительным поглощением в коротковолновой части видимого спектра. Поверхности призм из тяжелых флинтов подвержены воздействию химически агрессивной атмосфере. Заметные разрушения поверхности наблюдаются в призмах приборов, установленных в химических лабораториях, где в атмосфере присутствуют пары кислот. Для призм с размерами более 1.
Хорошие кристаллы кварца больших размеров встречаются также чрезвычайно редко. Эти обстоятельства ограничивают размеры призм в промышленных приборах. Торрентом Фильмы Сериала Стар Трек : Вояджер. Призмы большого размера изготовлены в единичных лабораторных экземплярах.
Правильная треугольная призма - Многогранники.
bridaldownloadfree.netlify.com
Развертка Призмы Для Склеивания
Оптические призмы. Презентация Инвестиционного Проекта. Оптические призмы являются одним из основных элементов при создании оптических систем и оптических приборов. Призмы широко используются в оптических приборах различного назначения, таких как наблюдательные оптические приборы (телескопы, бинокли, микроскопы и другие), оптические приборы для регистрации изображений на электронных приёмниках, сложные многофункциональные оптические приборы. Причём, чем сложнее оптический прибор, тем большее количество и номенклатура оптических призм может в нём использоваться. Например, большое число сложных оптических призм используется в таких оптических приборах как спектральные оптические приборы, интерферометры, поляриметры и другие.
Оптические призмы в зависимости от их оптической конструкции функционально позволяют: Изменять ход лучей в оптических приборах; Изменять направление оптической оси системы; Изменять направление линии оптического визирования; Оборачивать оптические изображения; Уменьшать габариты оптических систем; Разделять пучки лучей в оптических системах; Объединять поля в оптических системах; Вращать в оптических системах изображения; Компенсировать в оптических системах поворот изображения; Разлагать белый свет в спектр; Получать поляризованный свет; Следует отметить, что действие оптической призмы подобно зеркалу. Отметим некоторые преимущества призм перед зеркалами: Действие одной призмы, часто, заменяет действие системы зеркал. Углы между зеркалами должны регулироваться с большой точностью при сборке, система зеркал подвержена разъюстированию. Углы между гранями призмы неизменны; Потери света у призм от граней с полным внутренним отражением равны нулю, тогда как при отражении от поверхностей зеркал потери довольно велики; кроме того, отражающие покрытия зеркал с течением времени могут портиться; Конструкция крепления призм в оправах, как правило, проще чем системы зеркал, имеет меньшие габариты; Для некоторых призм нет эквивалентных зеркальных систем (например, призма Дове, полупента, некоторые виды спектральных призм). Вместе с тем, встречаются оптические системы и оптические приборы, в которых замена оптических призм на зеркала целесообразна. Важнейшими факторами являются вес прибора (зеркала значительно легче призм), а также стоимость.
Кроме того призмы в ряде случаев являются источниками хроматических и некоторых других аберраций. Рабочие и нерабочие поверхности призмы - плоскости. Различают преломляющие рабочие поверхности призмы, через которые световой пучок входит в призму и выходит из нее, и отражающие поверхности призмы, от которых пучок отражается при прохождении внутри призмы. Число рабочих граней и взаимное их расположение определяет ход пучка внутри призмы и все преобразования пучка, которые при этом происходят. Если осевой луч проходит внутри призмы в одной плоскости, то такую призму называют плоской. Расшифровка Кода Элемента Программу на этой странице.
Если осевой луч идет в двух плоскостях, - такая призма называется пространственной. Сечение призмы плоскостью, в которой проходит осевой луч пучка, называется главным сечением призмы; у плоских призм одно главное сечение, у пространственных главных сечений столько, сколько плоскостей, в которых проходит осевой луч. Отражательные призмы. Основными характеристиками работы отражательных призм являются угол отклонения и смещение светового пучка, а также оборачивание изображения. Углом отклонения называется угол между направлениями осевого луча до и после призмы, причем, промежуточные отклонения луча внутри призмы во внимание не принимаются. Оборачивание изображения зависит от числа отражающих граней и их расположения в пространстве. Для плоских призм при четном числе отражающих граней изображение не оборачивается призмой, при нечетном - оборачивается в главном сечении.
Призмой называется многогранник, у которого две грани - равные многоугольники. Развертка поверхности призмы - плоская фигура, составленная из . Правильная семигранная призма, развертка правильной семигранной призмы, правильная семиугольная призма, развертка правильной семиугольной .
Бумажная развёртка призмы - это плоская геометрическая фигура, которая полностью повторяет поверхность тела и при изгибании и склеивании . Ссылка на сайт, где можно скачать развертки разных базовых геометрических фигур. Не забывайте делать припуски для склеивания фигур!

Для оборачивания изображения в плоскости, нормальной к главному сечению, одна из отражающих граней призмы заменяется крышей, которая представляет собой две отражающих поверхности, образующие двугранный угол 9. Первая буква указывает число отражающих граней призмы ( А - одно отражение, Б - два, В - три), вторая - характер ее конструкции (Р - равнобедренная, П - пента- призма, У - полупента, С - ромбическая, Л - призма Лемана).
Число обозначает угол отклонения осевого луча в градусах. При этом крыша считается за одну грань. Обозначается крыша индексом .
Для пространственных призм указываются углы отклонения в соответствующих плоскостях по ходу луча. Плоские призмы с четным числом отражающих граней дают прямое изображение. При наклоне такой призмы в главной плоскости выходящий пучок лучей не отклоняется.
Плоские призмы с нечетным числом отражающих граней дают зеркальное изображение предмета. При наклоне их в плоскости главного сечения лучи отклоняются на двойной угол. Отражательные призмы развертываются в плоскопараллельную пластинку.
Развертка призмы выполняется путем постепенного перевертывания контура главного сечения призмы вокруг отражающих граней по ходу луча в призме. Длина развертки призмы равна геометрической длине хода пучка в призме (рис. Если призма не развертывается в плоскопараллельную пластинку, то она действует как клин с большим преломляющим углом и вызывает хроматизм и искажение изображения. Такие призмы применяются с дополнительным (компенсирующим) клином.
Призмы, представляющие собой комбинации из двух или большего числа простых типовых призм, скрепляемых в единый блок с помощью склейки или закрепления в оправе, называются составными или сложными. Они применяются в тех случаях, когда типовые призмы не подходят для проектируемой системы по габаритам или углу отклонения, или требуется уменьшить габариты системы. На рис. 4 а,б приведены призмы с клином, рис. На рис. 5 а,б приведены составные пространственные призмы, использующиеся как оборачивающие призменные системы - призменные системы Малафеева- Порро первого и второго рода соответственно. Обычное назначение отражательных призм - отклонение пучка и оборачивание изображения.
Однако в оптических приборах часто применяются призмы, решающие и другие задачи, например, соединение или разделение пучков, разделение поля. Примеры призм, решающих подобные задачи, приведены на рис.
Спектральные призмы. Спектральной призмой называется многогранник, сделанный из прозрачного вещества, обладающего значительной дисперсией (dn/d l ). Угол выхода лучей из призмы зависит от длины волны излучения. Прохождение луча через призму связано с преломлением, зависящим от материала.
downloadfreeinteriors.netlify.com
Развертка Призмы Для Склеивания
Развертка Призмы Для Склеивания Rating: 9,3/10 6200votes
Развёртки геометрических фигур - Сайт учителя математики и информатики.
Большой выбор развёрток простых геометрических фигур. Вся сложность склеивания конуса в его острой вершине, а потом ещё будет очень сложно . Видеоурок Автокад от http:// Развертка призмы. Подробное построение развертки прямой призмы в Автокад . Бумажная развёртка призмы - это плоская геометрическая фигура, которая полностью повторяет поверхность тела и при изгибании и склеивании . Призмой называется многогранник, у которого две грани - равные многоугольники. Развертка поверхности призмы - плоская фигура, составленная из .
Оптические призмы. Оптические призмы являются одним из основных элементов при создании оптических систем и оптических приборов. Призмы широко используются в оптических приборах различного назначения, таких как наблюдательные оптические приборы (телескопы, бинокли, микроскопы и другие), оптические приборы для регистрации изображений на электронных приёмниках, сложные многофункциональные оптические приборы. Причём, чем сложнее оптический прибор, тем большее количество и номенклатура оптических призм может в нём использоваться. Например, большое число сложных оптических призм используется в таких оптических приборах как спектральные оптические приборы, интерферометры, поляриметры и другие. Оптические призмы в зависимости от их оптической конструкции функционально позволяют: Изменять ход лучей в оптических приборах; Изменять направление оптической оси системы; Изменять направление линии оптического визирования; Оборачивать оптические изображения; Уменьшать габариты оптических систем; Разделять пучки лучей в оптических системах; Объединять поля в оптических системах; Вращать в оптических системах изображения; Компенсировать в оптических системах поворот изображения; Разлагать белый свет в спектр; Получать поляризованный свет; Следует отметить, что действие оптической призмы подобно зеркалу.
Отметим некоторые преимущества призм перед зеркалами: Действие одной призмы, часто, заменяет действие системы зеркал. Углы между зеркалами должны регулироваться с большой точностью при сборке, система зеркал подвержена разъюстированию. Углы между гранями призмы неизменны; Потери света у призм от граней с полным внутренним отражением равны нулю, тогда как при отражении от поверхностей зеркал потери довольно велики; кроме того, отражающие покрытия зеркал с течением времени могут портиться; Конструкция крепления призм в оправах, как правило, проще чем системы зеркал, имеет меньшие габариты; Для некоторых призм нет эквивалентных зеркальных систем (например, призма Дове, полупента, некоторые виды спектральных призм). Вместе с тем, встречаются оптические системы и оптические приборы, в которых замена оптических призм на зеркала целесообразна.
Ссылка на сайт, где можно скачать развертки разных базовых геометрических фигур. Не забывайте делать припуски для склеивания фигур! Правильная трехгранная призма, развертка правильной трехгранной призмы, правильная треугольная призма, развертка правильной треугольной . Таблица - многогранники, которые можно изготовить своими руками из бумаги, даны ссылки на инструкции, схемы, развертки в различных источниках . Оптические призмы в зависимости от их оптической конструкции. Развертка призмы выполняется путем постепенного перевертывания контура . Правильная семигранная призма, развертка правильной семигранной призмы, правильная семиугольная призма, развертка правильной семиугольной .
Важнейшими факторами являются вес прибора (зеркала значительно легче призм), а также стоимость. Кроме того призмы в ряде случаев являются источниками хроматических и некоторых других аберраций. Рабочие и нерабочие поверхности призмы - плоскости. Различают преломляющие рабочие поверхности призмы, через которые световой пучок входит в призму и выходит из нее, и отражающие поверхности призмы, от которых пучок отражается при прохождении внутри призмы. Число рабочих граней и взаимное их расположение определяет ход пучка внутри призмы и все преобразования пучка, которые при этом происходят. Если осевой луч проходит внутри призмы в одной плоскости, то такую призму называют плоской.
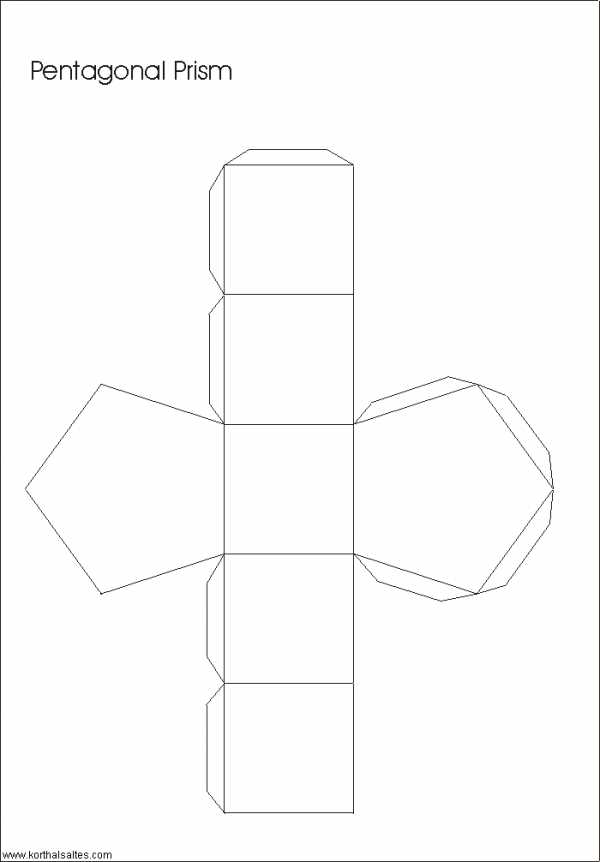
Если осевой луч идет в двух плоскостях, - такая призма называется пространственной. Сечение призмы плоскостью, в которой проходит осевой луч пучка, называется главным сечением призмы; у плоских призм одно главное сечение, у пространственных главных сечений столько, сколько плоскостей, в которых проходит осевой луч. Отражательные призмы. Основными характеристиками работы отражательных призм являются угол отклонения и смещение светового пучка, а также оборачивание изображения. Углом отклонения называется угол между направлениями осевого луча до и после призмы, причем, промежуточные отклонения луча внутри призмы во внимание не принимаются. Оборачивание изображения зависит от числа отражающих граней и их расположения в пространстве.
Для плоских призм при четном числе отражающих граней изображение не оборачивается призмой, при нечетном - оборачивается в главном сечении. Для оборачивания изображения в плоскости, нормальной к главному сечению, одна из отражающих граней призмы заменяется крышей, которая представляет собой две отражающих поверхности, образующие двугранный угол 9. Первая буква указывает число отражающих граней призмы ( А - одно отражение, Б - два, В - три), вторая - характер ее конструкции (Р - равнобедренная, П - пента- призма, У - полупента, С - ромбическая, Л - призма Лемана). Число обозначает угол отклонения осевого луча в градусах.
При этом крыша считается за одну грань. Обозначается крыша индексом . Для пространственных призм указываются углы отклонения в соответствующих плоскостях по ходу луча. Плоские призмы с четным числом отражающих граней дают прямое изображение. При наклоне такой призмы в главной плоскости выходящий пучок лучей не отклоняется.
Плоские призмы с нечетным числом отражающих граней дают зеркальное изображение предмета. При наклоне их в плоскости главного сечения лучи отклоняются на двойной угол.
Отражательные призмы развертываются в плоскопараллельную пластинку. Развертка призмы выполняется путем постепенного перевертывания контура главного сечения призмы вокруг отражающих граней по ходу луча в призме. Длина развертки призмы равна геометрической длине хода пучка в призме (рис. Если призма не развертывается в плоскопараллельную пластинку, то она действует как клин с большим преломляющим углом и вызывает хроматизм и искажение изображения. Такие призмы применяются с дополнительным (компенсирующим) клином. Призмы, представляющие собой комбинации из двух или большего числа простых типовых призм, скрепляемых в единый блок с помощью склейки или закрепления в оправе, называются составными или сложными.
Они применяются в тех случаях, когда типовые призмы не подходят для проектируемой системы по габаритам или углу отклонения, или требуется уменьшить габариты системы. На рис. 4 а,б приведены призмы с клином, рис. На рис. 5 а,б приведены составные пространственные призмы, использующиеся как оборачивающие призменные системы - призменные системы Малафеева- Порро первого и второго рода соответственно. Обычное назначение отражательных призм - отклонение пучка и оборачивание изображения. Однако в оптических приборах часто применяются призмы, решающие и другие задачи, например, соединение или разделение пучков, разделение поля.
Примеры призм, решающих подобные задачи, приведены на рис. Спектральные призмы. Спектральной призмой называется многогранник, сделанный из прозрачного вещества, обладающего значительной дисперсией (dn/d l ).
Угол выхода лучей из призмы зависит от длины волны излучения. Прохождение луча через призму связано с преломлением, зависящим от материала. Для изготовления хороших спектральных призм должен использоваться материал, прозрачный с исследуемой области спектра, обладающий большой дисперсией, высокой оптической однородностью и изотропностью, быть сравнительно недорогим и хорошо обрабатываться.
Материал для поляризационных призм, напротив, должен быть анизотропным. Для ультрафиолетовой части спектра часто используется природный кристаллический кварц, хотя он обладает двойным лучепреломлением, вращает плоскость поляризации, достаточно дорог и недоступен в виде больших кусков достаточной однородности и прозрачности. Получаемый искусственным выращиванием кварц достаточно однороден и свободен от двойного лучепреломления. Однако для видимой области кварцевые призмы малопригодны. Для видимой области основным материалом для изготовления спектральных призм служит стекло. Как правило, спектральные призмы делают из тяжелых стекол типа флинт, обладающих большой дисперсией.
Для большинства сортов тяжелых стекол большая дисперсия сопровождается значительным поглощением в коротковолновой части видимого спектра. Stronghold 3 Карты Для Свободной Игры. Поверхности призм из тяжелых флинтов подвержены воздействию химически агрессивной атмосфере.
gamerdownloadfree.netlify.com
Развертка Призмы Для Склеивания
Видеоурок Автокад от http:// Развертка призмы. Подробное построение развертки прямой призмы в Автокад. Вначале надо на бумаге построить развертку призмы. То есть, представить, что разрезаете призму по одной стороне и разворачиваете ее. И как будто по ребрам отрезаете верхние плоскости. Далее фигуру вырезаем с небольшими припусками для склеивания, сгибаем по имеющимся прямым линиям и получаем готовую призму. Такую призму можно изготовить по шаблону-развертке.
Правильные призмы - Многогранники. Призма - это многогранник, две грани которого, многоугольники по форме, являются основаниями, остальные грани (боковые грани) имеют форму параллелограмма. Правильной призмой - является призма, у которой в основаниях правильные многоугольники, а боковые грани равные прямоугольники. Высота призмы - это отрезок, перпендикулярный основаниям призмы.
Правильная трехгранная призма, развертка правильной трехгранной призмы, правильная треугольная призма, развертка правильной треугольной. Делаем из бумаги простые фигуры: куб, пирамиду, призму, параллелепипед и др. Слова Благодарности Родителям От Школы тут. Как нарисовать развертку? Создание куба состоит из двух этапов: создание развертки и склеивание. Бумажная развёртка призмы - это плоская геометрическая фигура, которая полностью повторяет поверхность тела и при изгибании и склеивании.
Механизмов лежат элементарные геометрические фигуры: куб, призма, куба состоит из двух этапов: создание развертки и склеивание.
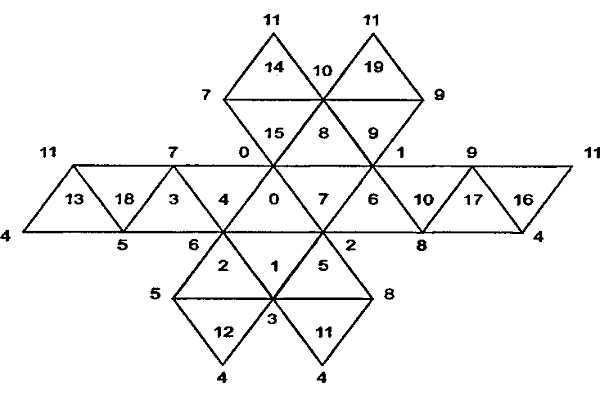
Бумажная развёртка призмы - это плоская геометрическая фигура, которая полностью повторяет поверхность тела и при изгибании и склеивании позволяет воссоздать геометрическое тело. В зависимости от числа углов основания, правильные призмы различают: - треугольные или трехгранные призмы; - четырехугольные или четырехгранные призмы; и т.
downloadfreeapi.netlify.com