Содержание
Пирамида — развертка. Развертка пирамиды для склеивания. Развертки из бумаги
Прямоугольник, квадрат, треугольник, трапеция и другие геометрические фигуры раздела точных наук. Пирамида — это многогранник. Основание этой фигуры — многоугольник, а боковые грани — треугольники с общей вершиной или трапеции. Для полного представления и изучения любого геометрического объекта изготавливаются модели. Они используют самые разные материалы, из которых сделана пирамида. Поверхность многогранной фигуры, развернутой на плоскости, называется разверткой. Метод преобразования плоских объектов в объемные многогранники и некоторые знания геометрии помогут создать макет. Подметать бумагой или картоном непросто. Вам понадобится умение делать чертежи по заданным размерам.
Содержание
- 1 Материалы и приспособления
- 2 Определение параметров
- 3 Как выполняется развертка правильной пирамиды?
- 4 Сборка макета
- 5 Развертка четырехугольной пирамиды
- 6 Завершающий этап выполнения макета
- 7 Объемные макеты сложных фигур
- 8 Построение чертежа
- 9 Завершение моделирования
- 10 Изготовление разных моделей многогранников
Материалы и приспособления
Моделирование и выполнение граненых объемных геометрических фигур — процесс интересный и увлекательный. Из бумаги можно сделать большое количество всевозможных макетов. Для работы вам понадобятся:
Из бумаги можно сделать большое количество всевозможных макетов. Для работы вам понадобятся:
- карандаш;
- управлять;
- ножницы;
- клей.
- бумага или картон;
- компас;
- ластик;
Определение параметров
Прежде всего, давайте определимся, какой будет пирамида. Развитие этой фигуры является основой для изготовления объемной фигуры. Выполнение работы требует максимальной точности. Если рисунок получится неверным, собрать геометрическую фигуру будет невозможно. Допустим, вам нужно сделать модель правильной треугольной пирамиды.
Любое геометрическое тело обладает определенными свойствами. Эта фигура имеет правильное многоугольное основание, а его вершина проецируется на ее центр. В качестве основы выбран равносторонний треугольник. Это условие определяет название. Боковые грани пирамиды представляют собой треугольники, количество которых зависит от многогранника, выбранного для основания. В этом случае их будет три. Также важно знать размеры всех составных частей, из которых будет составлена пирамида. Бумажные развертки выполняются в соответствии со всеми данными геометрической фигуры. Параметры будущей модели оговариваются заранее. Выбор используемого материала зависит от этих данных.
Также важно знать размеры всех составных частей, из которых будет составлена пирамида. Бумажные развертки выполняются в соответствии со всеми данными геометрической фигуры. Параметры будущей модели оговариваются заранее. Выбор используемого материала зависит от этих данных.
Как выполняется развертка правильной пирамиды?
Основа модели — лист бумаги или картона. Работа начинается с рисования пирамиды. Рисунок представлен в развернутом виде. Плоское изображение на бумаге соответствует заранее выбранным размерам и параметрам. У правильной пирамиды есть правильный многоугольник в основании, а ее высота проходит через ее центр. Для начала сделаем простую модель. В данном случае это треугольная пирамида. Определяет размер выбранной формы. Чтобы построить плоскую модель пирамиды, основанием которой является правильный треугольник, в центре листа с помощью линейки и карандаша нарисуйте основание заданных размеров. Далее с каждой ее стороны рисуем боковые грани пирамиды — треугольники. А теперь перейдем к их построению. Размеры сторон треугольников боковой поверхности измеряются циркулем. Ставим ножку циркуля вверху нарисованного основания и делаем насечку. Повторяем действие, переходя к следующей точке треугольника. Пересечение, полученное в результате этих действий, будет определять вершины боковых граней пирамиды. Соединяем их с основанием. Получаем рисунок пирамиды. Для наклеивания объемной фигуры по бокам боковых граней предусмотрены клапаны. Закончим рисовать маленькие трапеции.
А теперь перейдем к их построению. Размеры сторон треугольников боковой поверхности измеряются циркулем. Ставим ножку циркуля вверху нарисованного основания и делаем насечку. Повторяем действие, переходя к следующей точке треугольника. Пересечение, полученное в результате этих действий, будет определять вершины боковых граней пирамиды. Соединяем их с основанием. Получаем рисунок пирамиды. Для наклеивания объемной фигуры по бокам боковых граней предусмотрены клапаны. Закончим рисовать маленькие трапеции.
Сборка макета
Готовую конструкцию вырезаем по контуру ножницами. Аккуратно сложите развертку по всем линиям. Заполняем створки трапеции внутри фигуры таким образом, чтобы ее края сомкнулись. Соединяем их клеем. Через тридцать минут клей высохнет. Объемная фигура готова.
Развертка четырехугольной пирамиды
Для начала представим, как выглядит геометрическая фигура, макет которой будет составлен. Основание выбранной пирамиды — четырехугольник. Боковые ребра — треугольники. Для работы используем те же материалы и приспособления, что и в предыдущей версии. Рисуем карандашом на бумаге. В центре листа нарисуйте четырехугольник с выбранными параметрами.
Для работы используем те же материалы и приспособления, что и в предыдущей версии. Рисуем карандашом на бумаге. В центре листа нарисуйте четырехугольник с выбранными параметрами.
Разделите каждую сторону основы пополам. Рисуем перпендикуляр, который будет высотой треугольного лица. Раствором циркуля, равного длине боковой грани пирамиды, делаем насечки на перпендикулярах, поместив его ножку вверху основания. Соединяем оба угла одной стороны основания с получившейся точкой на перпендикуляре. В результате у нас получается квадрат в центре рисунка, по краям которого нарисованы треугольники. Чтобы закрепить модель на боковых гранях, добавьте вспомогательные клапаны. Для надежного крепления достаточно полосы шириной в один сантиметр. Пирамида готова к сборке.
Завершающий этап выполнения макета
Получившийся узор фигурки вырезается по контуру. Сложите бумагу по нарисованным линиям. Сбор объемной фигуры производится склейкой. Поставляемые клапаны смажьте клеем и закрепите полученным шаблоном.
Объемные макеты сложных фигур
Выполнив простой многогранный узор, можно переходить к более сложным геометрическим фигурам. Развернуть усеченную пирамиду выполнить намного сложнее. Его основы — подобные многогранники. Боковые кромки трапециевидные. Последовательность работы будет такой же, как и при изготовлении простой пирамиды. Зачистка будет более громоздкой. Для завершения рисунка воспользуйтесь карандашом, циркулем и линейкой.
Построение чертежа
Развитие усеченной пирамиды происходит в несколько этапов. Боковая грань усеченной пирамиды представляет собой трапецию, а основания — аналогичные многогранники. Допустим, они квадратные. На листе бумаги рисуем трапециевидную конструкцию с указанными размерами. Продлите стороны получившейся фигуры до пересечения. В результате у нас получается равнобедренный треугольник. Его сторону измеряем циркулем. На отдельном листе бумаги строим круг, радиус которого и будет измеренным расстоянием.
Следующий этап — построение боковых граней усеченной пирамиды. Разворачивание происходит внутри нарисованного круга. Нижнее основание трапеции измеряется циркулем. На круге отметьте пять точек, соединяющих линии в его центре. Получаем четыре равнобедренных треугольника. Отмеряем с помощью циркуля сторону нарисованной на отдельном листе трапеции. Накладываем это расстояние с каждой стороны нарисованных треугольников. Соединяем получившиеся точки. Боковые грани трапеции готовы. Осталось только нарисовать верхнее и нижнее основания пирамиды. В данном случае это аналогичные многогранники — квадраты. Нарисуйте квадраты на верхнем и нижнем основаниях первой трапеции. На чертеже показаны все части пирамиды. Развертка почти готова. Осталось только нарисовать соединительные створки по сторонам меньшего квадрата и одной из трапециевидных граней.
Разворачивание происходит внутри нарисованного круга. Нижнее основание трапеции измеряется циркулем. На круге отметьте пять точек, соединяющих линии в его центре. Получаем четыре равнобедренных треугольника. Отмеряем с помощью циркуля сторону нарисованной на отдельном листе трапеции. Накладываем это расстояние с каждой стороны нарисованных треугольников. Соединяем получившиеся точки. Боковые грани трапеции готовы. Осталось только нарисовать верхнее и нижнее основания пирамиды. В данном случае это аналогичные многогранники — квадраты. Нарисуйте квадраты на верхнем и нижнем основаниях первой трапеции. На чертеже показаны все части пирамиды. Развертка почти готова. Осталось только нарисовать соединительные створки по сторонам меньшего квадрата и одной из трапециевидных граней.
Завершение моделирования
Перед приклеиванием объемной фигуры рисунок вырезается по контуру ножницами. После этого скан аккуратно складывается по нарисованным линиям. Заливаем фиксирующие клапаны внутри модели. Склеиваем их между собой и прижимаем к граням пирамиды. Дайте модели высохнуть.
Склеиваем их между собой и прижимаем к граням пирамиды. Дайте модели высохнуть.
Изготовление разных моделей многогранников
Изготовление объемных моделей геометрических фигур — увлекательное занятие. Чтобы досконально освоить его, следует начать с простейших разверток. Постепенно переходя от простых поделок к более сложным выкройкам, можно приступать к созданию самых замысловатых дизайнов.
Развертка поверхности пирамиды с примерами в начертательной геометрии
Развертка поверхности пирамиды
Построение развертки боковой поверхности пирамиды по натуральным величинам ее ребер выполняется по следующему графическому алгоритму.
1-е действие. Построить на заданных проекциях пирамиды натуральные величины всех ее боковых ребер (например, способом вращения вокруг проецирующей прямой) и натуральные величины сторон многоугольника основания пирамиды (если основание лежит в плоскости уровня, то натуральные величины даны на одной из проекций).
2-е действие. Построить на свободном поле чертежа последовательно грани пирамиды по натуральным величинам ребер и натуральным величинам сторон основания (с помощью дуг-засечек) так, чтобы они имели общую вершину и примыкали друг к другу.
Построить на свободном поле чертежа последовательно грани пирамиды по натуральным величинам ребер и натуральным величинам сторон основания (с помощью дуг-засечек) так, чтобы они имели общую вершину и примыкали друг к другу.
3-е действие. Оформить чертеж развертки, выполнив линии сгиба по ребрам пирамиды тонкими штрихпунктирными линиями.
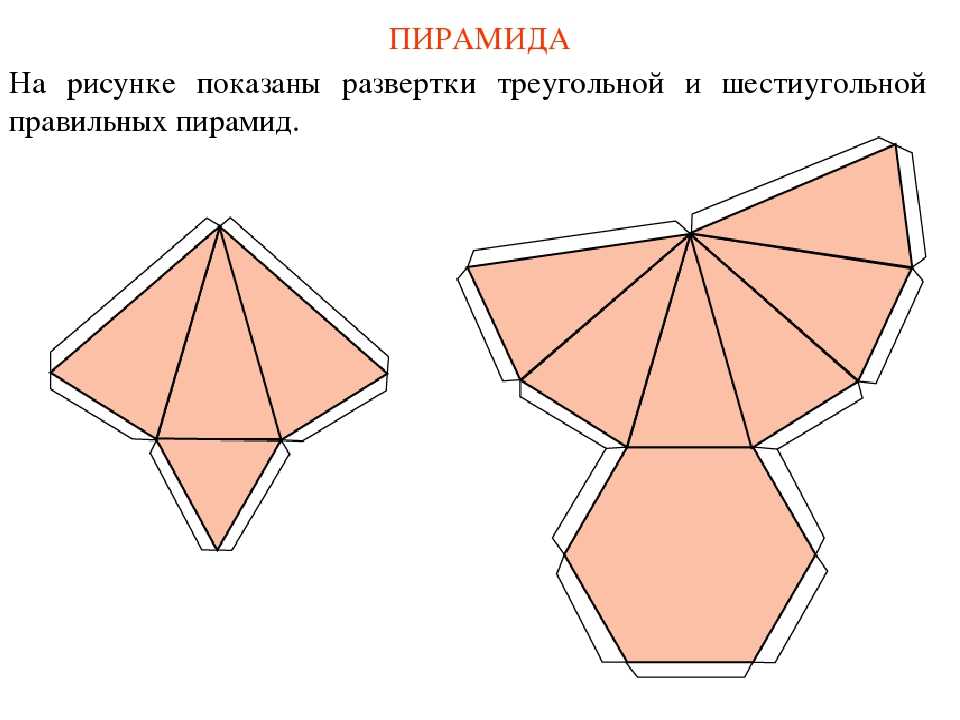
На рис. 9.3 показан пример построения развертки поверхности правильной треугольной пирамиды, основание которой треугольник на горизонтальной проекции имеет натуральные величины сторон, так как лежит в горизонтальной плоскости уровня.
Для построения развертки выполнены графические действия предложенного алгоритма.
1-е действие. Построить на заданной фронтальной проекции натуральные величины ребер пирамиды способом вращения вокруг горизонтально-проецирующей оси , проходящей через вершину пирамиды точку и совпадающую с ее высотой. Напоминаем графические действия этого способа преобразования:
1.1. Повернуть горизонтальные проекции ребер и вокруг оси так, чтобы они расположились параллельно фронтальной плоскости проекций (все ребра правильной пирамиды равны по длине), и получить совмещенные проекции точек .
1.2. На фронтальной проекции пирамиды конечные точки и ребер перемещаются по горизонтальной линии, перпендикулярной оси , и на пересечении с линией связи от точек построить точки .
1.3. Соединить вершину пирамиды с совпадающими точками — полученный отрезок и есть натуральная величина всех ребер пирамиды.
2-е действие. На свободном поле чертежа построить последовательно (например, против часовой стрелки) от ребра , по которому «разрезается» поверхность, треугольники граней пирамиды с общей вершиной следующим образом:
2.1. Провести дугу радиусом равным натуральной величине ребер пирамиды из произвольной точки плоскости чертежа.
2.2. На дуге отметить (произвольно) вершину основания точку , то есть построить ребро пирамиды.
2.3. На проведенной дуге засечками, равными длине сторон основания пирамиды отметить следующие точки вершин основания -в, С и точку А.
2.4. Построить треугольники граней пирамиды, соединив вершину с вершинами основания и достроить основание пирамиды к стороне, например, грани .
3-е действие. Оформить чертеж развертки, выполнив линии сгиба по ребрам пирамиды тонкими штрихпунктирными линиями с двумя короткими пунктирами.
Эта теория взята со страницы лекций для 1 курса по предмету «начертательная геометрия»:
Начертательная геометрия для 1 курса
Возможно эти страницы вам будут полезны:
Объем Гиперпирамиды
| Путь: физические идеи > основы > Расчет > |
На этой странице мы выведем формулу объема обычного n -мерного
гиперпирамида, то есть гиперпирамида, основанием которой является ( n-1 )-мерное
гиперкуб с длиной ребра r ,
и высота которого r .
Покажем, что объем такого п -пирамида
| (1) |
Это пример того, что мы могли бы легко найти с помощью исчисления.
Однако в данном случае мы планируем использовать его для разработки .
исчисление, поэтому нам нужно найти его каким-то другим способом. Собирались
к
продемонстрируйте это сначала чисто геометрическим аргументом, используя
картинки, а потом (поскольку это доказательство не вполне надежно) докажем
это символически, ближе к концу страницы.
| Рисунок 1: Выращивание пирамиды: |
n-пирамида или n
мерная гиперпирамида, аналогична треугольнику в произвольном
Габаритные размеры. Он формируется, начиная с (n-1)-куба, и заметая
куб перпендикулярен самому себе, точно так же, как мы делали это при формировании n
куб (см. гиперкубы
для обсуждения n -кубы и их объемы).
Однако по мере того, как мы его подметаем, мы уменьшаем его на на ,
линейно, с точностью до точки. Мы показываем это для 3-пирамиды на рисунке 1: Мы начинаем с квадрата
Мы показываем это для 3-пирамиды на рисунке 1: Мы начинаем с квадрата
и сметайте его, сжимая, чтобы сформировать пирамиду.
Хотя мы не нарисовали процесс ни для какого другого
размерность, нетрудно представить.
Что такое объем пирамиды? Для
треугольник, это (1/2) основание * высота. Для произвольной n -пирамиды
можно предположить, что n — том будет
(n-1)-объем основания, умножить на высота, умножить на
какая-то постоянная. Нам нужно подтвердить эту догадку, и мы
нужно
определить, какой может быть константа. Мы сделаем это по
упаковка n -куба с n -пирамидками,
и посмотреть, сколько нужно, чтобы точно заполнить его.
| Рисунок 2: Перекошенный треугольник |
Прежде чем мы приступим к нахождению объема, нам понадобится простая
наблюдение: Если
мы наклонить пирамиду (или любое простое тело), а
сохраняя ту же толщину поперечного сечения, она не меняется в
объем. Рискуя утомить очевидное, мы поговорим в какой-нибудь
Рискуя утомить очевидное, мы поговорим в какой-нибудь
длина об этом.
Мы можем увидеть это, представив, что разрезаем пирамиду
в стопку тарелок. Объем пирамиды равен сумме
объемов пластин. Перекос
пирамида просто скользит пластинами друг по другу; это не меняется
объем отдельных пластин и не меняет их количество,
и, следовательно, не меняет чистый объем пирамиды. Этот
показано для треугольника на рисунке 2.
Поскольку «толщина» пирамиды уменьшается в 9 раз.0009 линейно
от основания до вершины каждая пластина имеет форму точно такую же, как основание
(но в уменьшенном размере). Масштабный коэффициент для пластин варьируется
от 1
(у основания) до 0 (на вершине) и зависит от того, насколько далеко вверх по пирамиде
тарелка — но не от того, была ли она отодвинута в сторону.
Конечно, на нашем рисунке 2,
пластины довольно толстые, и я схитрил, показав их со скошенными краями.
края; сделать гладкий треугольник из пластин с «прямоугольником»
края,
вам нужно сделать пластины очень тонкими — бесконечно тонкими.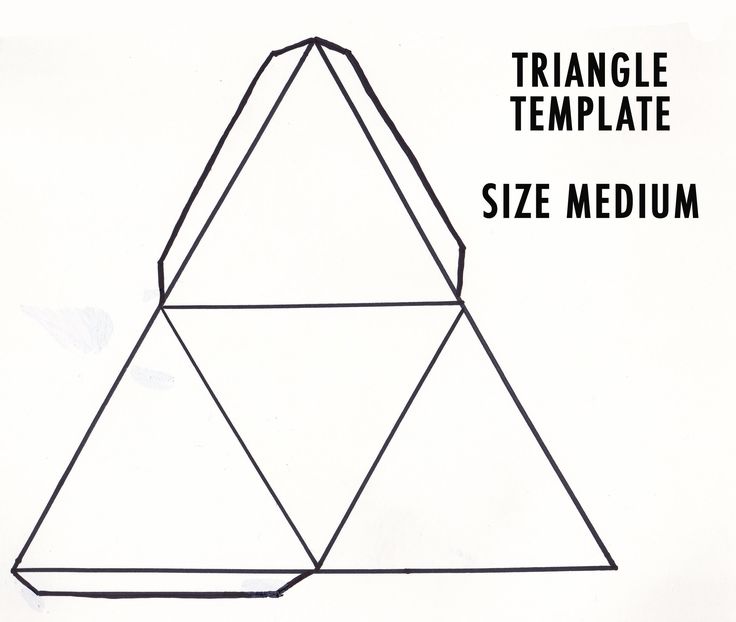
Давайте рассмотрим, что произойдет, если мы растянем
пирамида по вертикали. Мы можем изменить его высоту в k раз.
просто изменив толщину каждой пластины
на коэффициент, если k . Что
очевидно увеличивает объем каждой пластины в k раз ,
а так как объем пирамиды равен сумме объемов плит, то она также
изменяет объем пирамиды в 9 раз0009 к .
Аналогично, изменив площадь (или «( n -1)
объем») основания в с раз
в свою очередь, масштабирует объем каждой тарелки в с раз.
а также, и так по очереди масштабировать объем пирамиды на s
также. Таким образом, объем n -пирамиды равен
действительно линейный по высоте и объем n -1
база, и поэтому она должна быть просто константой, умноженной на эти значения.
Нам еще нужно найти константу.
Мы определили, что все n -пирамиды высотой r ,
и с размером r ( n -1)-кубов
для их баз, должны иметь одинаковый объем, поэтому мы можем выбрать любой
«форма» пирамиды для изучения.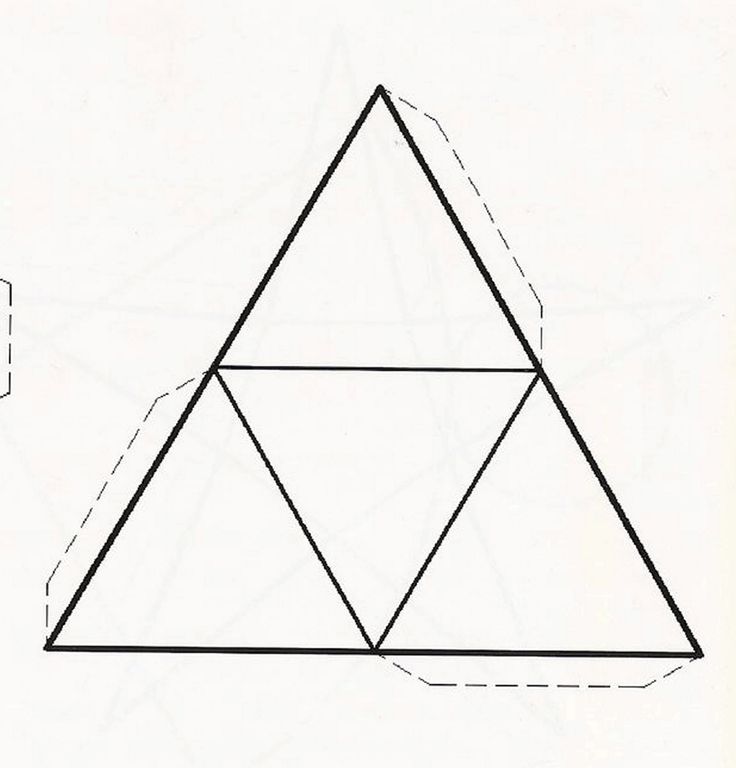 Для наших целей мы будем
Для наших целей мы будем
с использованием
справа пирамиды: Вершина расположена
прямо над одним
вершина основания, а одно из ребер, ведущих к вершине, пересекается
основание под прямым углом.
Сформируем правую n -пирамиду на боку ,
начиная с точки в начале координат. Мы отправим точку
по оси х , а при движении по оси
расширится, превратившись в ( n -1)-куб и увеличившись
линейно до тех пор, пока не переместится r
единиц вдоль оси, он вырастет в ( n -1)-куб
с ребрами длиной r .
Мы надеемся, что вскоре это станет яснее, когда мы приведем несколько примеров!
1-пирамиды … также известные как сегменты линии
Для пирамиды 1 эта операция просто производит
отрезок. «1-том» этой «1-пирамиды» равен r
ед., что, по сути, равно объему r
единица 1 -куб… не удивительно, так как «1 пирамида»
и «1 куб» — это просто отрезки линии.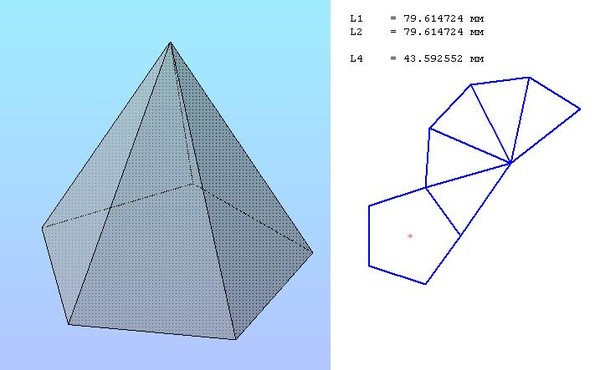 Итак, объем
Итак, объем
правильной 1-пирамиды:
2-пирамиды … или треугольники
| Фигура 3: Два треугольника в квадрате |
Для 2 -пирамиды,
получается прямоугольный треугольник, и когда мы пытаемся нарисовать результат, мы
поймите, что граница треугольника проходила по прямой
через квадрат. Операция фактически оставила нас ровно
достаточно
пространство, чтобы сделать это секунд раз, на этот раз «растущий»
треугольник вдоль оси y . (См. рис. 3). Мы можем установить два
треугольники в квадрат. Следовательно, мы только что подтвердили
то, что мы уже знали, это то, что
и, более конкретно, в конкретном случае, который нас интересует
с, база р
ед. ширины и высоты r
ед. , а «двухтомник» —
, а «двухтомник» —
3-пирамидки… Обычные «пирамидки»
| Рисунок 4а: Куб, заполняемый пирамидами:
|
Теперь мы входим на более интересную территорию. Прежде чем написать это
страницу Я не знал, что вы можете сделать то, что мы собираемся сделать: Мы
собирается упаковать три пирамиды в куб, точно заполнив его.
| Рисунок 4б: Пирамида на оси X: |
Начнем с построения пирамиды по x
оси, должны так, как мы построили треугольник на x
оси в предыдущем разделе: Мы начнем с точки в
исходное положение и сдвиньте его на r единиц в
право. На самом деле наша «точка» — это квадрат нулевого размера 9.0010 .
На самом деле наша «точка» — это квадрат нулевого размера 9.0010 .
По мере того, как он будет двигаться вправо, мы вырастем его,
до тех пор, пока он не переместится на р единиц
по оси x это будет r x r
площадь. Пирамиду выметет, r
ед. высокие, с r x r
база. Это показано на рисунке
4б. Обратите внимание, что пирамида лежит на
сторона . Обратите также внимание, что мы не заполнили дно,
так как казалось легче понять картину, нарисованную таким образом.
Теперь нам нужно кое-что понять о гиперкубах: они симметричны
по отношению к осям — смена осей не меняет
очевидная форма куба. Гиперкуб или обычный 3-куб
— имеет точно такую же структуру вдоль каждой оси. Следовательно,
на самом деле не было никакой разницы из каких осей мы «выращивали» нашу пирамиду
вместе; мы могли бы вставить его в куб в любом случае.
На рисунках с 5а по 5с мы показали пирамиду, лежащую на x , вставленные в куб, показанный на рисунке 4a, и мы показали эквивалентные пирамиды вдоль осей y и z , также встроенные в куб.
| Рисунок 5а: Пирамида на Х, в кубе: | Рисунок 5б: Пирамида на Y, в кубе: | Рисунок 5с: Пирамида по Z, в кубе: |
На рисунке 6a показаны пирамиды x и y , обе вставленные в куб, и, наконец, на рисунке 6b.
мы показываем все три пирамиды в кубе. Рассматривание лиц
пирамиды, лежащие внутри куба, и отметив, как они подходят
вместе, мы можем видеть, что они действительно должны точно заполнить куб,
так же, как они нарисованы.
Итак, мы видим, что объем правильной 3-пирамиды с основанием R Квадрат единиц, а также с высотой R , должен быть
Примечание , когда просмотр рис.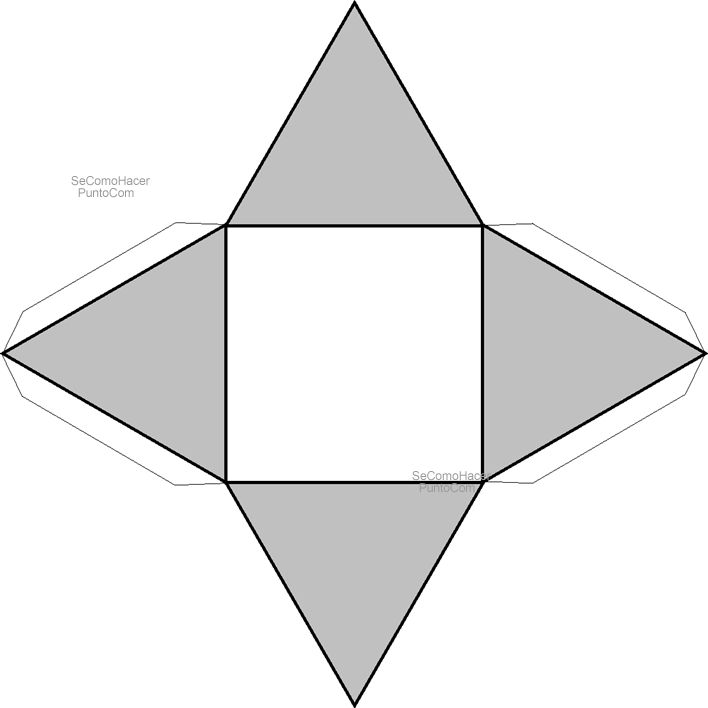 .
.
К сожалению, перспективные рисунки могут быть обманчивы, и это
довольно легко «увидеть» общую вершину на рисунке (6b) как лежащую в
центр куба!
| Рисунок 6а: Пирамиды на X и Y: | Рисунок 6б: 3 пирамиды в кубе: просмотров |
Общие n-пирамиды
Опять же, мы должны иметь в виду тот факт, что гиперкубы симметричны относительно любой перестановки осей.
Имея это в виду, если мы представим, что начинаем с куба нулевой размерности ( n -1) в начале координат и перемещаем его вдоль оси x , увеличивая его по ходу, мы можем «видим», что мы будем производить n -пирамида, лежащая на оси x , так же, как мы построили сначала треугольник, а затем квадрат вдоль оси x
ось. Мы также можем видеть… возможно, смутно… что мы можем сделать
Мы также можем видеть… возможно, смутно… что мы можем сделать
одна и та же точная операция вдоль каждой оси, и кажется очевидным, что грани
должны «подходить друг к другу», когда мы выполняем эту операцию.
Следовательно, мы можем заполнить n -куб ровно n гиперпирамидами, а объем обычного N Dimensional Hyperpyramid должен быть
Альтернативный геометрический аргумент
| Рисунок 7: квадратный немного более сложный аргумент, который может быть легче изобразить. Вместо того, чтобы начинать с точки в начале координат, давайте начнем с n куба, р шт на ребро. Выберите одну из его граней, которая сама по себе является кубом n -1. Проведите грань точно перпендикулярно самой себе, прямо через центр n -куба и на напротив грани . Это
Полезно изобразить это, чтобы нарисовать 3 -куб Символическое доказательствоПриведенные выше аргументы лучше всего можно охарактеризовать как «мотивирующие» результат. Поскольку мы не можем на самом деле изобразить, что происходит в измерениях n , они не являются надежным доказательством. Итак, теперь мы представим краткое алгебраическое доказательство. Мы знаем, что вершины N Cube, R единиц на краю, состоящий из всех точек, для которых каждая координата составляет 0 или R : (с.1) . Региона содержит в кубе n состоит из всех точек, лежащих в пределах r единиц от начала координат по каждой оси: (стр.2) 0009 k ось представляет собой область, заметаемую ( n -1)-кубом по мере его движения вдоль оси k , растущая по ходу движения. (стр.3) Pick Если, с другой стороны, значения x и — это все разных , тогда найди (стр.4) Итак, точка лежит в пирамиде вдоль оси k . Более того, Следовательно, каждая точка, не лежащая на грани, лежит в ровно одна пирамид. Есть n осей, есть n пирамид, значит объем n -пирамид Небольшое обобщение Мы Более того, форма В качестве альтернативы, Через три
| ||||
 Но вот в чем хитрость: сжимается во время движения — сжимается в два раза быстрее, чем движется , так что когда оно перемещается на r /2 единиц (и только что достигло центра n куб), он уменьшился до нуля. А затем снова вырастите его, чтобы, когда он переместился в общей сложности на r единиц и достиг противоположной грани, он снова вырос до своего начального размера. Мы можем сделать это снова , раз для каждой оси, и, поскольку каждая грань линейно сжимается до точек по мере движения к центру, они не будут «сталкиваться».
Но вот в чем хитрость: сжимается во время движения — сжимается в два раза быстрее, чем движется , так что когда оно перемещается на r /2 единиц (и только что достигло центра n куб), он уменьшился до нуля. А затем снова вырастите его, чтобы, когда он переместился в общей сложности на r единиц и достиг противоположной грани, он снова вырос до своего начального размера. Мы можем сделать это снова , раз для каждой оси, и, поскольку каждая грань линейно сжимается до точек по мере движения к центру, они не будут «сталкиваться».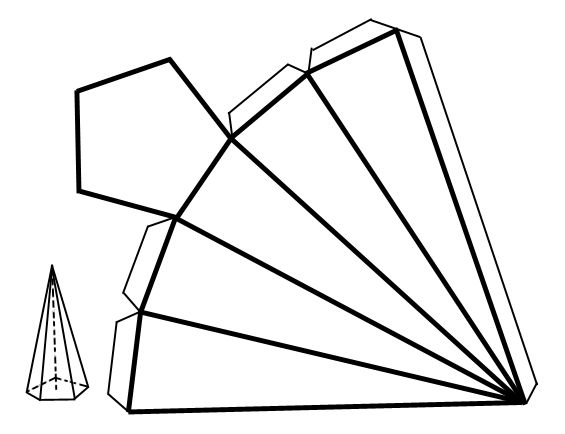 К сожалению, в то время как я сделал набросок такого
К сожалению, в то время как я сделал набросок такого В точке s единиц от начала координат на оси k куб будет иметь s единиц на стороне. Следовательно, в этой точке все координаты всех точек этого ( n -1)-куба должны лежать в пределах s единиц 0. Это может звучать так, будто мы описываем сферу, но это не так… мы ограничиваем значение каждой координатой , а не общим расстоянием от начала координат. Набор точек, содержащихся в такой пирамиде, должен быть:
В точке s единиц от начала координат на оси k куб будет иметь s единиц на стороне. Следовательно, в этой точке все координаты всех точек этого ( n -1)-куба должны лежать в пределах s единиц 0. Это может звучать так, будто мы описываем сферу, но это не так… мы ограничиваем значение каждой координатой , а не общим расстоянием от начала координат. Набор точек, содержащихся в такой пирамиде, должен быть:

