Таблица расчета веса стального листа – Первая Металлобаза

Вы находитесь в разделе Справочной информации.

Если вам нужно узнать цену и рассчитать точный вес предполагаемого заказа, перейдите по ссылке в соответствующий раздел: Лист.

Одним из наиболее востребованных видов металлопроката является стальной лист. Он может использоваться как готовый продукт или в качестве заготовки для дальнейшего производства. При выборе листов для тех или иных целей стоит учитывать разновидности, технические характеристики и особенности изготовления плоского металлопроката.

Сферы применения листов металла обширны, а их свойства и характеристики во многом зависят от способа изготовления. Так, формовка стального проката может происходить методами горячего или холодного проката.

Горячее деформирование осуществляется путем нагрева металла до температур, превышающих условия его рекристаллизации и составляющих 60% и более от температуры плавления. Нагретую заготовку прокатывают между валками, а после формовки обрабатывают, убирая возможные дефекты и следы окалины. Регламентируется размер листа горячекатанного ГОСТом 19903-2015, по которому рулонный прокат имеет толщину не более 25 мм, при ширине 500-2200 мм.

Горячекатаные листы не отличаются высокой точностью и гладкостью поверхности, но их доступность позволяет использовать такой металл повсеместно в народном хозяйстве, во многих видах строительства и производства, в том числе в качестве заготовок для изготовления просечно-вытяжных листов, сварных балок, электросварных и профильных труб и уголка.

Метод холодного проката предполагает формовку металла катками без предварительного прогрева, что требует больше времени и усилий. В результате получается лист с гладкой поверхностью, высокой прочностью на изгиб, растяжение и разрыв. Регулируется производство листов холоднокатаных ГОСТами 19904-90, 9045-93, 16523-97, согласно которым их толщина варьируется от 0,28 до 5мм, а ширина от 500 до 2350 мм.

Такой прокат пользуется спросом в строительстве, космической отрасли, машино- и судостроении, и в качестве заготовок при производстве посуды, мебели, оборудования, бытовых приборов и инструментов. Нанесение цинкового слоя повышает антикоррозийные свойства, что применяется при изготовлении профнастила.

При маркировке стальных листов учитываются их разновидности по нескольким критериям:

• Вид проката:

— г/к – горячекатаный, х/к – холоднокатаный;

— ОЦ – оцинкованный, ОК – с полимерным покрытием, ПК – под окраску;

— ромб, чечевица – для листа рифленого ГОСТ 8568-77.

• По точности проката: А – повышенной, Б – нормальной.
• Ровность поверхности: ПО – особо высокая, ПВ – высокая, ПУ – улучшенная, ПН – нормальная.
• Размерные параметры листа указываются цифрами, в миллиметрах.
• Обработка кромки: НО – необрезная, О – обрезная.
• Отделка поверхности: І – особо высокая, ІІ – высокая, III – повышенная, IV – обычная.
• Поверхность: Т – травленая, ГЛ – глянцевая, М – матовая.
• Свойства вытяжения: ВОСВ – весьма особо сложной, ОСВ – особо сложной, СВ – сложной, ВГ – весьма глубокой вытяжки.
• Наличие узора кристаллизации у оцинкованных листов: КР – есть, МТ – нет.
• Для профилированных листов: Н – для настила покрытий, НС – для настила и стеновых ограждений, С – для стеновых ограждений.
• Класс прочности: 295; 315; 345; 355; 390.

Также в маркировке указываются марка стали с обозначением Ст, и номер ГОСТа или ТУ, которым соответствуют указанные параметры.

Вес листа

Масса листа зависит от его технических характеристик, способа производства и типа сплава, который был использован при производстве.

Вес листового металла, также можно рассчитать самостоятельно с помощью простых математических формул.

Формула расчета веса листа металла: m = a * b * t * ρ

a – ширина;

b – длина;

t – толщина;

ρ – плотность.

Лист стальной: ГОСТ

Производство листового проката регламентируют следующие стандарты:

1. ГОСТ 19903-2015 определяет сортамент горячекатаного проката в листах и рулонах толщиной от 1,2 до 25,0 мм.
2. ГОСТ 19904-90 используется для холоднокатаного проката толщиной от 0,35 до 3,50 мм.
3. В зависимости от видов используемых металлов в части производства толстолистового металлопроката: ГОСТ 1577-93 для конструкционной, ГОСТ 4041-2017 для горячекатаной нелегированной конструкционной стали, ГОСТ Р 58915-2020 – для криогенных металлов.
4. Для изготовления тонких листов применяются технические условия: ГОСТ 3836-83 для электротехнической нелегированной, ГОСТ 11268-76 – для легированной стали;
5. Выпуск листов жаростойкого и жаропрочного проката, устойчивого к коррозии: ГОСТ 24982-81 определяет общие технические условия, ГОСТ 5582-75 используется в части проката тонколистового, ГОСТ 7350-77 – толстолистового.
6. ГОСТ 8568-77 нормирует изготовление листов, имеющих ромбическое или чечевичное рифление.
7. ГОСТ 9234-74 регламентирует сортамент листовых стальных профилей.
8. Оцинкованная холоднокатаная сталь с полимерным покрытием производится в соответствии с ГОСТ 34180-2017 при горячем покрытии цинком, и по ГОСТ 34649-2020 для электролитической оцинковки.

Ранее регламентировалось изготовление просечно-вытяжнго листа ГОСТом 8706-78, который был отменен. На данный момент используются технические условия 36-26.11-5-89, которые содержат требования к техническим параметрам и сортаменту данного вида проката.

Технические характеристики профлиста.

Сортамент листового проката, его виды, типы и характеристики – Блог 【БилдФикс】

Листовой прокат — это вид плоского металлопроката, производимый способом горячей прокатки на прокатных станах.

❗ Различают следующие виды листового проката: толстый горячекатаный прокат, тонкий горячекатаный, тонкий холоднокатаный прокат.

Сначала получают толстый прокат путем горячей прокатки металла при температуре свыше 1700 градусов по Фаренгейту, что значительно превышает порог рекристаллизации стали. В результате этого процесса металл становится достаточно пластичным, менее твердым и прочным, что необходимо для последующей его обработки.

Однако в результате такого сильного нагрева металла на его поверхности образуется окалина, что при последующей обработке может стать причиной структурных и поверхностных дефектов, у такого проката менее точные и более округлые углы, а также невысокая точность по толщине.

Для получения тонколистовой продукции и улучшения точности размеров горячекатаный лист предварительно очищают от окалины и оксидной пленки, а потом подвергают холодной прокатке, проходящей при температурах ниже начала рекристаллизации. Толщина холоднокатаного стального листа после прокатки не превышает 5 мм, его поверхность качественная, ровная.

Сортамент и типы листового проката

⭐ Сортамент листового проката регламентируется ГОСТами, строгое соответствие которым позволяет изготавливать металл заданных свойств и требуемых потребительских качеств.

Согласно ГОСТ 19 903–2015, толстый прокат изготавливают в листах толщиной 4 -160 мм или либо в рулонах толщиной до 25 мм. Ширина листа зависит от типа прокатного стана и может быть 500−4500 мм, ширина рулонов 500 — 2200 мм. Наиболее распространенным является металлопрокат из углеродистой стали обыкновенного качества марки Ст3 либо низколегированной марки стали 09Г2С с химическим составом по ГОСТ 380.

Горячекатаный прокат используется в качестве подката для холоднокатаного проката, а в виде готовой продукции он нашел широкое применение в строительстве, автомобилестроении, мостостроении, судостроении, востребован в производстве сварных труб и гнутого профиля.

Тонкий горячекатаный лист поставляется толщиной 1,2- 4 мм и в листах либо рулонах в соответствии ГОСТ 16 523–89 из углеродистой качественной стали и стали обыкновенного качества с химическим составом по ГОСТ 1050–88.

Холоднокатаный лист изготавливается в соответствии с требованиями ГОСТ 19 904–90, 9045−93, 16 523−97 толщиной 0,25 — 5 мм, шириной 500 — 2350 мм. Наиболее распространенным является холоднокатаный прокат из качественных углеродистых сталей, низколегированных или легированных сталей. В результате холодной деформации горячекатаного проката происходит изменение свойств продукции, в результате чего у холоднокатаного металлопроката повышается точность размеров, улучшается качество поверхности, повышается прочность и твердость, снижаются характеристики пластичности.

Холоднокатаный лист нашел широкое применение во всех сферах народного хозяйства. Он используется в производстве оцинкованного металлопроката, профилированного листа, в автомобилестроении, в изготовлении пищевой продукции, электротехнике.

Характеристики листового проката

Сама технология изготовления листового проката предусматривает получение готовой продукции с высокими техническими и эксплуатационными характеристиками, такими как:

• прочность и надежность;
• длительность службы;
• стойкость к коррозии, изменениям температуры, атмосферным осадкам и другим природным явлениям;
• хорошая обрабатываемость, свариваемость, проведение термообработки, улучшающей свойства плоского металла;
• устойчивость к деформациям;
• широкий ареал применения.

Особенности листового проката

Особенности листового проката, его эксплуатационные свойства, долговечность и другие характеристики зависят от легирующих добавок, используемых в процессе производства стали:

• Кремний повышает устойчивость изделий к ударным нагрузкам;
• Хром, титан, никель, молибден снижают риск образования коррозии;
• Медь улучшает пластичность;
• Молибден и вольфрам повышают устойчивость к высоким температурам;
• Ванадий создает лист со стабильной и равномерной структурой.

Применение

Все изготавливаемые типы листового проката находят широкое применение в:

• машиностроении, станкостроении, автомобилестроении, энергетике;
• химической, нефтехимической, бумажной, пищевой, мебельной промышленности;
• строительстве, архитектуре, ландшафтном дизайне;
• сельском и народном хозяйстве, в быту.

Учитывая характеристики листового проката, из него штампуются отдельные запчасти, детали, крепежные элементы.

Из полосового материала изготавливаются различные емкости, тара, пищевая, медицинская, лабораторная посуда.

Металл применяется для обшивки бытовок, создания различных конструкций, устройства ограждений, производства ступеней на металлических лестницах.

Учебное пособие по оптимизации — пошаговый пример сочетания продуктов в Excel

Основные шаги

Чтобы определить модель оптимизации в Excel, выполните следующие основные шаги: способ.

Выберите ячейку электронной таблицы для хранения значения каждой переменной решения в вашей модели.

В рамках этой общей структуры у вас есть большая гибкость в том, как вы выбираете ячейки для хранения переменных и ограничений вашей модели, а также какие формулы и встроенные функции вы используете. В общем, ваша цель должна состоять в том, чтобы создать электронную таблицу, которая четко и понятно излагает свое назначение.

Создание рабочего листа Excel

Предполагая, что вы организовали данные для задачи в Excel, следующим шагом будет создание рабочего листа, на котором вычисляются формулы для целевой функции и ограничения .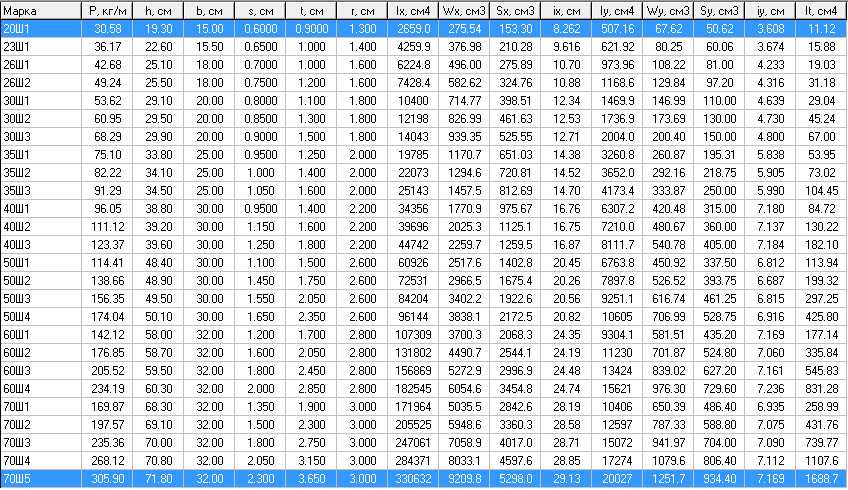 Поскольку переменные решения и ограничения обычно входят в логические группы, вам часто потребуется использовать диапазоны ячеек в электронной таблице для их представления.

На листе ниже мы зарезервировали ячейки B4, C4, D4 и E4 для представления переменных решения X ₁ , X ₂ , X ₃ и X ₄ , представляющие количество поддонов каждого типа панелей, которые необходимо произвести. Решатель определит оптимальные значения для этих ячеек. (Нажмите на рабочий лист, чтобы увидеть изображение в полном размере.)

Обратите внимание, что прибыль от каждого поддона с панелями (450, 1150, 800 и 400 долларов США) была введена в ячейки B5, C5, D5 и E5 соответственно. Это позволяет нам вычислить цель в ячейке F5 как:

         Формула для ячейки F5:    =B5*B4+C5*C4+D5*D4+E5*E4

или аналогичный,

         Формула для ячейки F5:    =СУММПРОИЗВ(B5:E5,B4:E4)

В ячейки B8:E11 мы ввели количество ресурсов, необходимых для производства поддона каждого типа панелей. Например, значение 15 в ячейке C9 означает, что для изготовления поддона панелей в тихоокеанском стиле требуется 15 часов прессования. Эти числа получены непосредственно из формул для ограничений, показанных ранее. Имея эти значения, мы можем ввести формулу в ячейку F8, чтобы вычислить общее количество клея, используемого для любого количества произведенных поддонов:

        Формула для ячейки F8:    =СУММПРОИЗВ(B8:E8,$B$4:$E$4)

Мы можем скопировать эту формулу в ячейки F9:F11 для вычисления общего количества прессованной, сосновой и дубовой щепы использовал. (Знаки доллара в $B$4:$E$4 указывают, что этот диапазон ячеек остается постоянным, а диапазон ячеек B8:E8 становится B9:E9, B10:E10 и B11:E11 в скопированных формулах.) Формулы в ячейках F8:F11 соответствуют левым значениям ограничений.

В ячейки G8:G11 мы ввели доступное количество ресурсов каждого типа (соответствующих значениям ограничений в правой части). Это позволяет нам выразить ограничения , показанные ранее как:

        F8:F11<=G8:G11

Это эквивалентно четырем ограничениям: F8<=G8, F9<=G9, F10<=G10 и F11<=G11.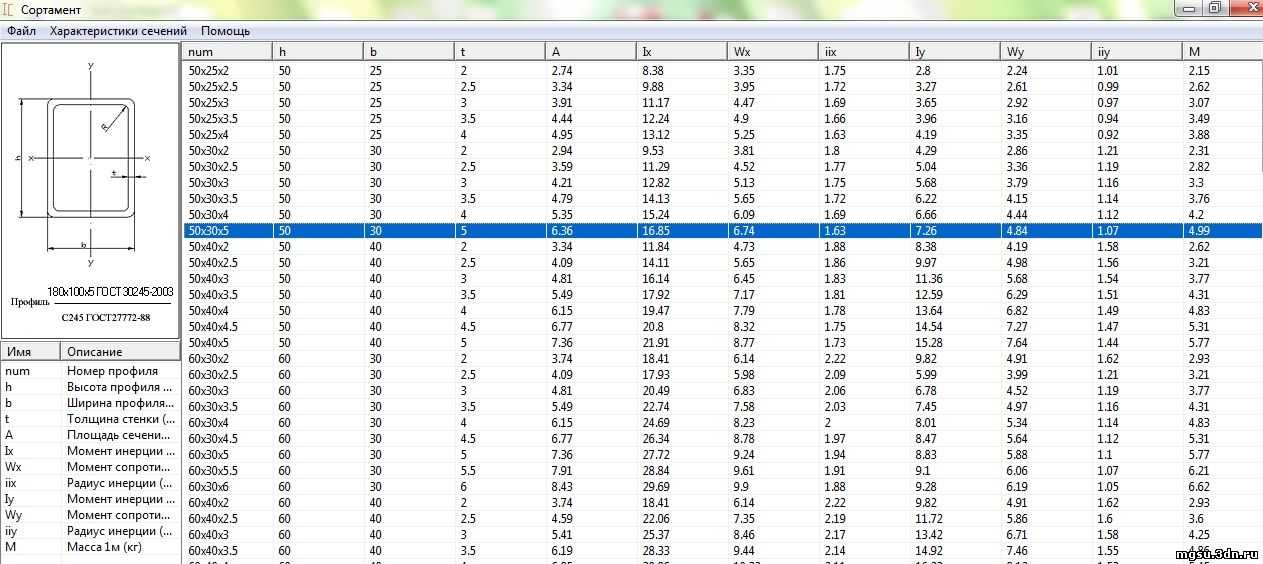 Мы можем ввести этот набор ограничений непосредственно в диалоговых окнах Решателя вместе с условиями неотрицательности : 

        B4:E4 >= 0

Нажмите на приведенные ниже ссылки, чтобы узнать, как эту модель можно решить с помощью встроенного Решателя Excel (или Решателя премиум-класса) или с помощью флагманского продукта Risk Solver Platform от FrontLine Systems.

< Вернуться к: Пример набора продуктов
<< Вернуться к: Начало учебного курса Далее: Использование Решателя Excel >
Далее: Использование платформы Решателя рисков >

Использование Решателя для определения оптимального ассортимента продуктов1

В этой статье обсуждается использование Solver, надстройки Microsoft Excel, которую можно использовать для анализа возможных вариантов, чтобы определить оптимальное сочетание продуктов.

Как определить месячный ассортимент продукции, обеспечивающий максимальную прибыльность?

Компаниям часто необходимо определить количество каждого продукта, которое необходимо производить ежемесячно. В своей простейшей форме задача о наборе продуктов заключается в том, как определить количество каждого продукта, которое должно быть произведено в течение месяца, чтобы максимизировать прибыль. Ассортимент продукции обычно должен соответствовать следующим ограничениям:

• Набор продуктов не может использовать больше ресурсов, чем доступно.

• На каждый товар существует ограниченный спрос. Мы не можем производить в месяц больше продукта, чем диктует спрос, потому что лишнее производство тратится впустую (например, скоропортящийся препарат).

Давайте теперь решим следующий пример задачи о наборе продуктов. Вы можете найти решение этой проблемы в файле Prodmix.xlsx, показанном на рисунке 27-1.

Допустим, мы работаем в фармацевтической компании, которая производит шесть различных продуктов на своем заводе. Производство каждого продукта требует рабочей силы и сырья. В строке 4 на рис. 27.1 показаны часы труда, необходимые для производства фунта каждого продукта, а в строке 5 показаны фунты сырья, необходимые для производства фунта каждого продукта. Например, для производства фунта Продукта 1 требуется шесть часов труда и 3,2 фунта сырья. Для каждого лекарства цена за фунт указана в строке 6, удельная стоимость за фунт указана в строке 7, а доля прибыли в расчете на фунт указана в строке 9.. Например, Продукт 2 продается по цене 11,00 долларов за фунт, имеет удельную стоимость 5,70 долларов за фунт и приносит прибыль 5,30 долларов за фунт. Месячный спрос на каждое лекарство указан в строке 8. Например, спрос на продукт 3 составляет 1041 фунт. В этом месяце доступно 4500 часов труда и 1600 фунтов сырья. Как эта компания может максимизировать свою ежемесячную прибыль?

Если бы мы ничего не знали о Excel Solver, мы бы решили эту проблему, создав рабочий лист для отслеживания прибыли и использования ресурсов, связанных с набором продуктов.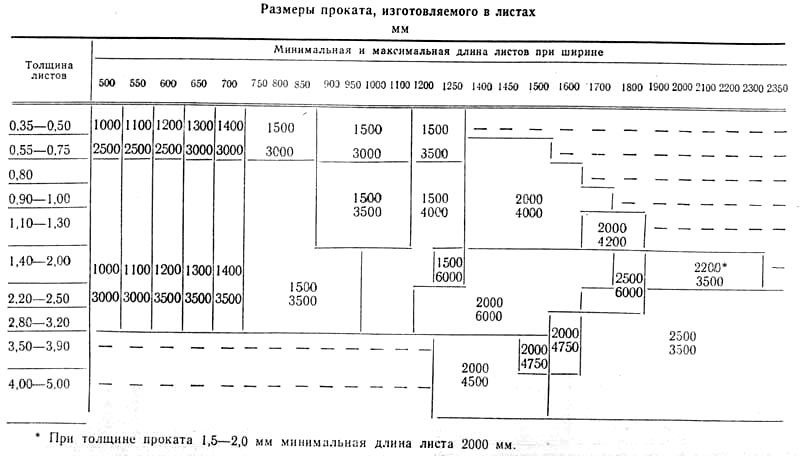 Затем мы будем использовать метод проб и ошибок, чтобы варьировать ассортимент продукции для оптимизации прибыли, не используя больше рабочей силы или сырья, чем доступно, и не производя никаких лекарств сверх спроса. Мы используем Солвер в этом процессе только на этапе проб и ошибок. По сути, Solver — это механизм оптимизации, который безупречно выполняет поиск методом проб и ошибок.

Ключом к решению проблемы ассортимента продукции является эффективное вычисление использования ресурсов и прибыли, связанной с любым набором продуктов. Важным инструментом, который мы можем использовать для выполнения этих вычислений, является функция СУММПРОИЗВ. Функция СУММПРОИЗВ умножает соответствующие значения в диапазонах ячеек и возвращает сумму этих значений. Каждый диапазон ячеек, используемый в оценке СУММПРОИЗВ, должен иметь одинаковые размеры, что означает, что вы можете использовать СУММПРОИЗВ с двумя строками или двумя столбцами, но не с одним столбцом и одной строкой.

В качестве примера того, как мы можем использовать функцию СУММПРОИЗВ в нашем примере с набором продуктов, давайте попробуем вычислить использование наших ресурсов.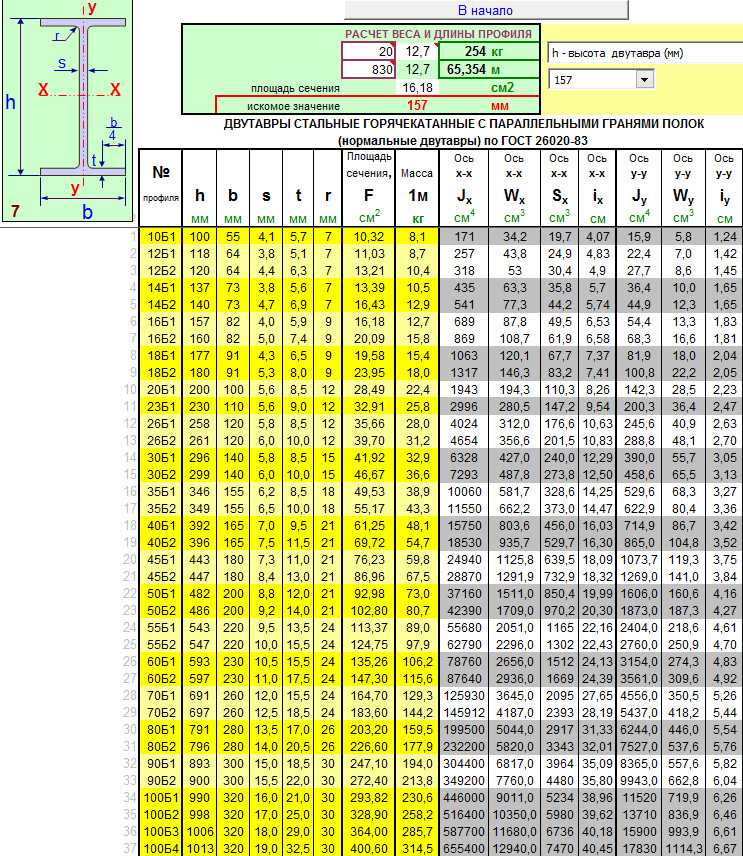 Наше использование рабочей силы рассчитывается на

(Затраты труда на фунт наркотика 1)*(Произведенный фунт наркотика 1)+

(Затраты труда на фунт наркотика 2)*(Произведено 2 фунта наркотика) + …

(Затраты труда на фунт наркотика 6)*(Произведено 6 фунтов наркотика)

Мы могли бы вычислить использование рабочей силы более утомительным способом: D2*D4+E2*E4+F2*F4+G2*G4+h3*h5+I2*I4 . Точно так же использование сырья можно рассчитать как D2*D5+E2* E5+F2*F5+G2*G5+h3*H5+I2*I5 . Однако ввод этих формул в рабочую таблицу для шести продуктов занимает много времени. Представьте, сколько времени это заняло бы, если бы вы работали с компанией, которая произвела, например, 50 продуктов на своем заводе. Гораздо проще вычислить использование труда и сырья, скопировав из D14 в D15 формулу 9.0105 СУММПРОИЗВ($D$2:$I$2,D4:I4) . Эта формула вычисляет D2*D4+E2*E4+F2*F4+G2*G4+h3*h5+I2*I4 (это наше использование труда), но ее гораздо проще ввести! Обратите внимание, что я использую знак $ с диапазоном D2:I2, поэтому при копировании формулы я по-прежнему получаю набор продуктов из строки 2. Формула в ячейке D15 вычисляет использование сырья.

Аналогичным образом наша прибыль определяется

(Прибыль препарата 1 на фунт)*(Произведено фунта препарата 1) +

(Прибыль препарата 2 на фунт)*(Производство препарата 2 фунта) + …

(Прибыль препарата 6 на фунт)*(Производство препарата 6 фунтов)

Прибыль легко вычислить в ячейке D12 по формуле СУММПРОИЗВ(D9:I9,$D$2:$I$2) .

Теперь мы можем идентифицировать три компонента нашей модели Solver для набора продуктов.

• Целевая ячейка. Наша цель — максимизировать прибыль (вычисляется в ячейке D12).

• Изменение ячеек. Количество произведенных фунтов каждого продукта (указано в диапазоне ячеек D2:I2)

• Ограничения. У нас есть следующие ограничения:

  • Не используйте больше рабочей силы или сырья, чем доступно. То есть значения в ячейках D14:D15 (используемые ресурсы) должны быть меньше или равны значениям в ячейках F14:F15 (доступные ресурсы).

  • Не производить больше препарата, чем требуется. То есть значения в ячейках D2:I2 (фунты, произведенные каждым наркотиком) должны быть меньше или равны спросу на каждый наркотик (указанному в ячейках D8:I8).

  • org/ListItem»>

    Мы не можем произвести отрицательное количество любого лекарства.

Я покажу вам, как ввести целевую ячейку, изменить ячейки и ограничения в Солвере. Тогда все, что вам нужно сделать, это нажать кнопку «Решить», чтобы найти сочетание продуктов, максимизирующее прибыль!

Для начала щелкните вкладку Данные и в группе Анализ щелкните Решатель.

Примечание.  Как объяснялось в главе 26 «Введение в оптимизацию с помощью Excel Solver», Solver устанавливается нажатием кнопки Microsoft Office, затем «Параметры Excel» и «Надстройки». В списке «Управление» выберите «Надстройки Excel», установите флажок «Надстройка решения», а затем нажмите «ОК».

Появится диалоговое окно Solver Parameters, как показано на рисунке 27-2.

Щелкните поле «Установить целевую ячейку», а затем выберите нашу ячейку прибыли (ячейка D12). Щелкните поле «Изменение ячеек», а затем укажите диапазон D2:I2, который содержит количество фунтов, произведенных каждым лекарством. Теперь диалоговое окно должно выглядеть, как показано на рис. 27-3.

Теперь мы готовы добавить в модель ограничения. Нажмите кнопку «Добавить». Вы увидите диалоговое окно Add Constraint, показанное на рисунке 27-4.

Чтобы добавить ограничения на использование ресурсов, щелкните поле Ссылка на ячейку и выберите диапазон D14:D15. Выберите <= из среднего списка. Щелкните поле Ограничение и выберите диапазон ячеек F14:F15. Диалоговое окно Add Constraint теперь должно выглядеть так, как показано на рис. 27-5.

Теперь мы добились того, что когда Решатель пробует разные значения для меняющихся ячеек, только те комбинации, которые удовлетворяют обоим D14<=F14 (затраченная рабочая сила меньше или равна доступной рабочей силе) и D15<=F15 (использованное сырье меньше или равно доступному сырью). Щелкните Добавить, чтобы ввести ограничения спроса. Заполните диалоговое окно Add Constraint, как показано на рисунке 27-6.

Добавление этих ограничений гарантирует, что, когда Solver пробует различные комбинации для меняющихся значений ячеек, будут рассматриваться только комбинации, удовлетворяющие следующим параметрам:

• D2<=D8 (количество произведенного Лекарства 1 меньше или равно спросу на Лекарство 1)

• E2<=E8 (количество произведенного Лекарства 2 меньше или равно спросу на Лекарство 2)

• F2<=F8 (количество производимого Лекарства 3 меньше или равно спросу на Лекарство 3)

• org/ListItem»>

  G2<=G8 (количество производимого Лекарства 4 меньше или равно спросу на Лекарство 4)

• h3<=H8 (количество произведенного лекарства 5 меньше или равно спросу на лекарство 5)

• I2<=I8 (количество производимого Лекарства 6 меньше или равно спросу на Лекарство 6)

Нажмите кнопку «ОК» в диалоговом окне «Добавить ограничение». Окно Solver должно выглядеть так, как показано на рис. 27-7.

Мы вводим ограничение, согласно которому изменение ячеек должно быть неотрицательным, в диалоговом окне «Параметры решения». Нажмите кнопку «Параметры» в диалоговом окне «Параметры решателя». Установите флажок «Предполагать линейную модель» и поле «Предполагать неотрицательное», как показано на рис. 27-8 на следующей странице. Нажмите «ОК».

Установка флажка «Предполагать неотрицательное» гарантирует, что «Поиск решения» будет учитывать только комбинации изменяющихся ячеек, в которых каждая изменяющаяся ячейка принимает неотрицательное значение. Мы установили флажок «Предполагать линейную модель», поскольку задача о наборе продуктов представляет собой особый тип задачи «Решатель», называемый линейной моделью . По сути, модель Solver является линейной при следующих условиях:

• Целевая ячейка вычисляется путем сложения членов формы (изменяющаяся ячейка)*(константа) .

• Каждое ограничение удовлетворяет «требованиям линейной модели». Это означает, что каждое ограничение оценивается путем сложения членов формы (изменяющаяся ячейка) * (константа) и сравнения сумм с константой.

Почему эта задача Решателя является линейной? Наша целевая ячейка (прибыль) вычисляется как

.

(Прибыль препарата 1 на фунт)*(Производство фунта препарата 1) +

(Прибыль препарата 2 на фунт)*(Производство препарата 2 фунта) + …

(Прибыль препарата 6 на фунт)*(Производство препарата 6 фунтов)

Это вычисление следует шаблону, в котором значение целевой ячейки получается путем сложения членов формы (изменяющаяся ячейка) * (константа) .

Наше трудовое ограничение оценивается путем сравнения значения, полученного из (Затраты труда на фунт лекарства 1)*(Производство фунтов лекарства 1) + (Затраты труда на фунт лекарства 2)*(Производство фунтов лекарства 2)+ …(Затраты труда ед на фунт лекарства 6)*( Препарат 6 фунтов произведен) в наличии.

Таким образом, трудовое ограничение оценивается путем сложения членов формы (изменяющаяся ячейка) * (константа) и сравнения сумм с константой. И ограничение по труду, и ограничение по сырью удовлетворяют требованиям линейной модели.

Наши ограничения спроса принимают форму

(Лекарство 1 произведено)<=(Спрос на лекарство 1)

(Лекарство 2 произведено)<=(Спрос на Лекарство 2)

§
(Произведено лекарство 6)<=(Спрос на лекарство 6)

Каждое ограничение спроса также удовлетворяет требованию линейной модели, поскольку каждое оценивается путем сложения членов формы (изменяющаяся ячейка)*(постоянная) и сравнивая суммы с константой.

Показав, что наша модель ассортимента продукции является линейной моделью, почему нас это должно волновать?

• org/ListItem»>

  Если модель Решателя является линейной и мы выбираем Предполагать линейную модель, Решатель гарантированно найдет оптимальное решение для модели Решателя. Если модель Solver не является линейной, Solver может найти или не найти оптимальное решение.

• Если модель Решателя является линейной и мы выбираем Предполагать линейную модель, Решатель использует очень эффективный алгоритм (симплексный метод) для нахождения оптимального решения модели. Если модель Solver является линейной и мы не выбираем Assume Linear Model, Solver использует очень неэффективный алгоритм (метод GRG2) и может столкнуться с трудностями при поиске оптимального решения модели.

После нажатия OK в диалоговом окне Solver Options мы возвращаемся к основному диалоговому окну Solver, показанному ранее на рис. 27-7. Когда мы нажимаем «Решить», Solver вычисляет оптимальное решение (если оно существует) для нашей модели ассортимента продуктов. Как я говорил в главе 26, оптимальным решением для модели ассортимента продуктов будет набор изменяющихся значений ячеек (фунтов, произведенных каждым лекарством), который максимизирует прибыль по сравнению с набором всех возможных решений. Опять же, допустимое решение — это набор изменяющихся значений ячеек, удовлетворяющих всем ограничениям. Изменение значений ячеек показано на рис. 27-9.являются допустимым решением, потому что все уровни производства неотрицательны, уровни производства не превышают потребности, а использование ресурсов не превышает доступных ресурсов.

Изменение значений ячеек, показанное на рис. 27-10 на следующей странице, представляет собой недопустимое решение по следующим причинам:

• Мы производим больше Лекарства 5, чем требуется.

• org/ListItem»>

  Мы используем больше рабочей силы, чем доступно.

• Мы используем больше сырья, чем есть в наличии.

После нажатия кнопки «Решить» Solver быстро находит оптимальное решение, показанное на рис. 27-11. Вам нужно выбрать Keep Solver Solution, чтобы сохранить оптимальные значения решения на листе.

Наша фармацевтическая компания может максимизировать свою ежемесячную прибыль на уровне 6 625,20 долларов США, производя 596,67 фунта Наркотика 4, 1084 фунта Наркотика 5 и ни одного другого наркотика! Мы не можем определить, сможем ли мы достичь максимальной прибыли в размере 6 625,20 долларов США другими способами. Все, в чем мы можем быть уверены, так это в том, что с нашими ограниченными ресурсами и спросом мы не сможем заработать больше $6 627,20 в этом месяце.

Предположим, что спрос на каждый продукт должен быть удовлетворен. (См. рабочий лист No Feasible Solution в файле Prodmix.xlsx.) Затем мы должны изменить наши ограничения спроса с D2:I2<=D8:I8 до D2:I2>=D8:I8 . Для этого откройте Solver, выберите зависимость D2:I2<=D8:I8, а затем нажмите кнопку «Изменить». Появится диалоговое окно «Изменить ограничение», показанное на рис. 27-12.

Выберите >= и нажмите OK. Теперь мы уверены, что Solver рассмотрит возможность изменения только тех значений ячеек, которые соответствуют всем требованиям. Когда вы нажмете «Решить», вы увидите сообщение «Решатель не смог найти подходящее решение». Это сообщение не означает, что мы допустили ошибку в нашей модели, а скорее то, что с нашими ограниченными ресурсами мы не можем удовлетворить спрос на все продукты. Solver просто говорит нам, что если мы хотим удовлетворить спрос на каждый продукт, нам нужно добавить больше труда, больше сырья или больше того и другого.

Давайте посмотрим, что произойдет, если мы допустим неограниченный спрос на каждый продукт и позволим производить отрицательное количество каждого лекарства. (Вы можете увидеть эту проблему Решателя на рабочем листе Set Values ​​Do Not Converge в файле Prodmix.xlsx.) Чтобы найти оптимальное решение для этой ситуации, откройте Решатель, нажмите кнопку «Параметры» и снимите флажок «Предполагать неотрицательное». . В диалоговом окне «Параметры решателя» выберите ограничение потребности D2:I2<=D8:I8, а затем нажмите «Удалить», чтобы удалить ограничение. Когда вы нажимаете «Решить», «Поиск решения» возвращает сообщение «Установить значения ячеек не сходятся». Это сообщение означает, что если целевая ячейка должна быть максимизирована (как в нашем примере), существуют допустимые решения с произвольно большими значениями целевой ячейки. (Если целевая ячейка должна быть минимизирована, сообщение «Установить значения ячеек не сходятся» означает, что существуют возможные решения с произвольно малыми значениями целевых ячеек.) В нашей ситуации, допуская отрицательное производство лекарства, мы фактически «создаем ресурсы, которые можно использовать для производства сколь угодно больших количеств других наркотиков. Учитывая наш неограниченный спрос, это позволяет нам получать неограниченную прибыль. В реальной ситуации мы не можем заработать бесконечное количество денег. Короче говоря, если вы видите «Установленные значения не сходятся», в вашей модели действительно есть ошибка.

1. Предположим, что наша фармацевтическая компания может купить до 500 часов рабочей силы по цене на 1 доллар в час больше, чем текущая стоимость рабочей силы. Как мы можем максимизировать прибыль?

2. На заводе по производству микросхем четыре техника (A, B, C и D) производят три продукта (Продукты 1, 2 и 3). В этом месяце производитель чипов может продать 80 единиц продукта 1, 50 единиц продукта 2 и не более 50 единиц продукта 3. Техник А может производить только продукты 1 и 3. Техник Б может производить только продукты 1 и 2. Техник C может производить только Продукт 3. Техник D может производить только Продукт 2. Каждая произведенная единица продукции приносит следующую прибыль: Продукт 1 — 6 долларов; Продукт 2, 7 долларов; и Продукт 3, 10 долларов. Время (в часах), необходимое каждому специалисту для производства продукта, составляет:

   Продукт	Техник А	Техник Б	Техник С	Техник Д
   1	2	2,5	Не могу	Не могу
   2	Не могу	3	Не могу 904:00	3,5
   3	3	Не могу	4	Не могу

3. org/ListItem»>

   Каждый техник может работать до 120 часов в месяц. Как производитель микросхем может максимизировать свою ежемесячную прибыль? Предположим, что можно произвести дробное количество единиц.

4. Завод по производству компьютеров производит мыши, клавиатуры и джойстики для видеоигр. Прибыль на единицу, использование труда на единицу, месячный спрос и использование машинного времени на единицу приведены в следующей таблице:

   	Мыши	Клавиатуры	Джойстики
   Прибыль/единица	$8	11 долларов	$9
   Использование труда/единица	. 2 часа 904:00	.3 часа	.24 часа
   Машинное время/ед.	.04 часа	.055 час	.04 часа
   Ежемесячная потребность	15 000	27 000	11 000

5. org/ListItem»>

   Каждый месяц доступно 13 000 рабочих часов и 3 000 часов машинного времени. Как производитель может максимизировать свой ежемесячный вклад в прибыль от завода?

6. Решите наш пример с лекарством, предполагая, что минимальный спрос на каждое лекарство должен составлять 200 единиц.

7. Джейсон делает бриллиантовые браслеты, ожерелья и серьги. Он хочет работать максимум 160 часов в месяц. У него 800 унций бриллиантов. Прибыль, рабочее время и унции алмазов, необходимые для производства каждого продукта, приведены ниже. Если спрос на каждый продукт неограничен, как Джейсон может максимизировать свою прибыль?

   Продукт	Удельная прибыль	Рабочее время на единицу	Унций алмазов на единицу
   Браслет	$300	.