Нормальные конусности и углы

Источник: ГОСТ 8593-81 

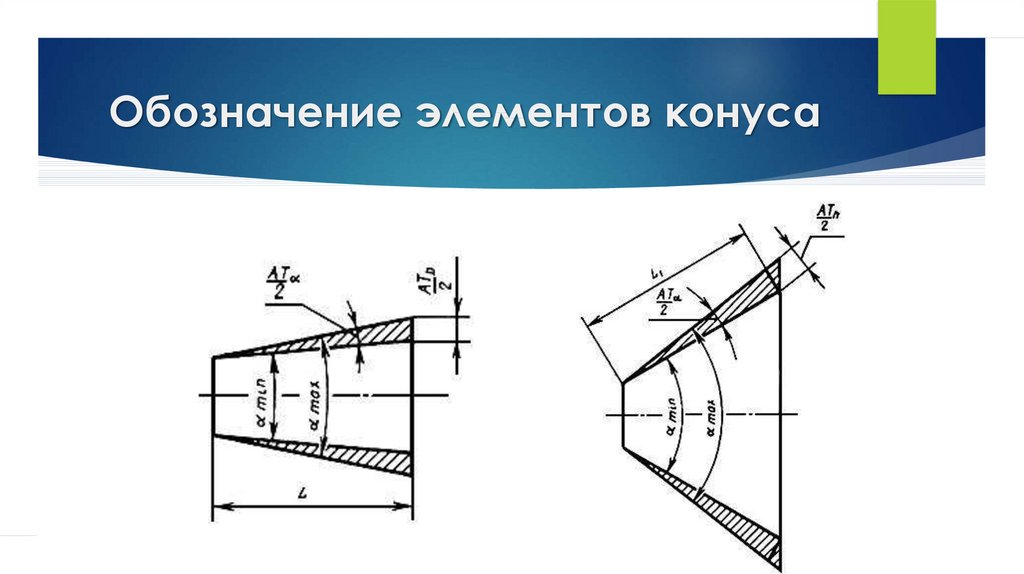
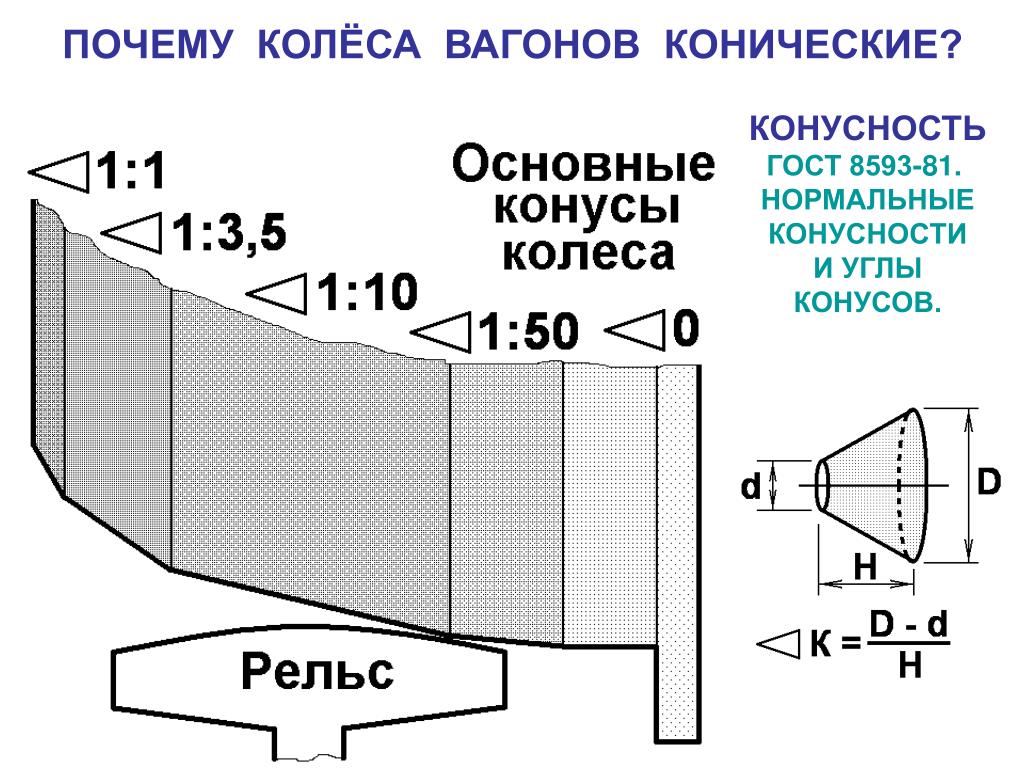
Конусность К есть отношение разности диаметров двух поперечных сечений конуса к расстоянию между ними.

Уклон «i» есть отношение разности размеров двух поперечных сечений к расстоянию между ними.

Таблица 1. Углы конусности

К оглавлению

Величины угла конуса в соединении имплантат-абатмент

Янв 15, 2018 | НОВОСТИ, СТАТЬИ

Угол конуса в соединении имплантат-абатмент получила довольно широкое распространение. Нет смысла в рамках данного поста детально обсуждать имеет ли решающее значение значение величины угла конуса, как это влияет на герметичность соединения и микроподвижность ортопедического элемента установленного в имплантате.

Мы бы хотели коснуться другого вопроса. Каждый производитель имплантационной системы заявляет определенные значения угла конуса в конического типа соединениях между имплантатом и абатментом. Часто мы можем видеть в каталоге, например: «Угол конического соединения 12 градусов». Так написано во многих каталогах. Но в реальности угол углу рознь. Часть производителей указывает в каталоге величину полного угла конического соединения, а часть только половину значения величины угла, отталкиваясь от угла не между сторонами конуса, а между одной из сторон конуса и вертикалью. Если Вы решите проверить, например, у некоторых производителей, о каком контректно угле идет речь, то столкнетесь с тем, с чем столкнулись мы. Ни в одном их каталоге не указано и не изображено о каком конкретно угле идет речь. Написано просто «угол конического соединения 12 градусов». И найти информацию о том, какой конкретно угол имеется в виду не представляется возможным, т.к. нигде ничего нет.

Для того чтобы разобраться с этим вопросом нам пришлось провести свое небольшое исследование уровня начальной школы. Методология такова — берем бумажный каталог какого-либо производителя, находим там достаточно большое изображение ортопедического элемента, чтобы можно было на нем произвести простое измерение с помощью школьного транспортира. Сначала мы чертим линии параллельные сторонам конуса в соединении, потом вычисляем и чертим вертикаль (она же является биссектрисой) по центру (ну или оси) ортопедического элемента. Далее накладываем транспортир, совмещаем линии конуса и метки транспортира таким образом, чтобы добиться их безусловной параллельности. После этого мы фиксируем точки совпадения линий конуса с метками измерительной шкалы транспортира и фиксируем получившиеся значения. Таким образом мы и получаем искомое значение угла конического соединения.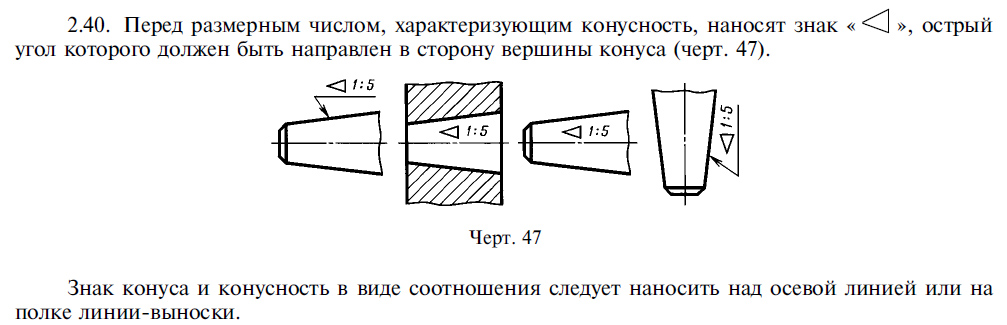

Первое измерение мы провели на нашей системе MIS. Несмотря на то, что каталоге MIS указан угол конического соединения, а также приведены чертежи, говорящие о каком конкретно угле идет речь, мы провели данный опыт, так сказать, для чистоты эксперимента. MIS заявляет, что угол конического соединения равен 12 градусов. Обратите внимание на фотографию. Действительно, значение полного угла конического соединения составляет 12 градусов. А значение угла между центральной осью (вертикалью) и одной из сторон конуса составляет 6 градусов. Несмотря на то, что каталоге MIS указан угол конического соединения, а также приведены чертежи, говорящие о каком конкретно угле идет речь, мы провели данный опыт, так сказать, для чистоты эксперимента.

Следующее измерение мы произвели на имплантационной системе одно из корейских производителей. В каталоге кроме текста «угол 12 градусов» найти обозначения, картинки или чертежи позволяющие идентифицировать о каком конкретно угле идет речь, не представилось возможным. Мы произвели соответствующие описанным выше манипуляции и получили следующие результаты. Значение угла между вертикалью (осью) получилось равным 12 градусам. А значение полного угла равным, соответственно 24 градусам.

Таким образом, произведя измерения углов конусов двух систем мы получили два следующих значения:
1. Полный угол конического соединения производителя MIS равен 12 градусам.
2. Полный угол конического соединения корейского производителя равен 24 градусам.

Калькулятор конусности

Создано Рахулом Дхари

Отзыв Стивена Вудинга

Последнее обновление: 17 октября 2022 г.

Содержание:

• Что такое конусность?
• Типы конусности
• Как рассчитать конусность на фут?
• Пример: Использование калькулятора конусности
• Применение конусов
• Часто задаваемые вопросы

Калькулятор конусности предназначен для определения параметров, связанных с сужением заготовки . Конус похож на усеченный конус (см. калькулятор площади усеченного конуса) с двумя концами разных размеров. В современных автоматизированных производственных процессах ручная регулировка выравнивания инструмента может оказаться устаревшей. Но вам все равно нужно подставить цифры нужных размеров, чтобы получилась коническая заготовка.

Сверлильные патроны, оправки, гвозди, болты и винты являются одними из наиболее распространенных применений конусов. Различные параметры для сужения включают длину, диаметры и угол конусности . Читайте дальше, чтобы понять, что такое конусность и как рассчитать конусность на дюйм?

Что такое конусность?

Конусообразование — это процесс механической обработки заготовки в виде конического профиля , т. е. постепенного уменьшения размеров одного конца по отношению к длине . Его также можно сравнить с усеченным конусом или усеченным конусом . Учитывая круглое поперечное сечение (см. калькулятор площади поперечного сечения) заготовки, сечение на большем конце называется большая секция и имеет диаметр как большой диаметр Dl D_\mathrm{l} Dl​, тогда как меньшая секция известна как второстепенная секция и диаметр является второстепенным диаметром ( Ds D_\mathrm{s} Дс). Элементы конуса:

• Длина конуса ( TlT_\mathrm{l} Tl​): Расстояние между второстепенной и большой частями заготовки.
• Конусность на дюйм ( TPI ): Уменьшение диаметра поперечного сечения на дюйм длины. Для заготовки с длиной конуса Tl T_\mathrm{l} Tl​ формула конусности на дюйм:

TPI=(Dl−Ds)Tl\qquad \mathrm{TPI} = \frac{(D_\mathrm{l} — D_\mathrm{s} )}{T_\mathrm{l}}TPI=Tl​( Dl​−Ds​)​

Приведенная выше формула изменена следующим образом для расчета конусности на фут, TPF :

TPI=12(Dl−Ds)Tl\qquad \mathrm{TPI} = 12 \frac {(D_\mathrm{l} — D_\mathrm{s} )}{T_\mathrm{l}}TPI=12Tl​(Dl​−Ds​)​

• Угол конусности ( θ ): Угол между центральной линией и наклонной стороной. Угол конусности определяется уравнением: 9{-1}(\mathrm{TPI}/2)θ=tan−1(TPI/2)

  Конусная заготовка

  Конусы можно указать с помощью трех параметров:

  • Главный диаметр;
  • Малый диаметр; и
  • Длина конуса.

  Типичный конус может быть указан с использованием трех указанных выше размеров. Тем не менее, некоторые другие способы упомянуть конус — это следующие комбинации параметров.

  • Основной диаметр, длина конуса и конусность на фут или дюймы.
  • Наибольший диаметр, вспомогательный диаметр и сквозная длина.
  • Наибольший диаметр, меньший диаметр и угол конусности.

  Преобразователи длины
  Посетите наш конвертер длины или калькулятор футов и дюймов, если вам нужна помощь в преобразовании.

  Типы конусов

  Некоторые из распространенных типов конусов классифицируются на основе:

  • Размер – конусы Ярно, Метрические, Брауна и Шарпа, Морзе и Джейкобса.
  • Расположение – Внутренние и внешние конусы.
  • Применение – Самоудерживающиеся и быстросъемные конусы.

  Как рассчитать конусность на фут?

  Для расчета конусности на фут:

  1. Введите большой диаметр , DlD_\mathrm{l}Dl​.
  2. Заполните меньший диаметр , DsD_\mathrm{s}Ds​.
  3. Вставка длина конуса , TlT_\mathrm{l}Tl​.
  4. Калькулятор угла конусности вернет значение конусности на дюйм или фут и угол конусности .

  Пример: С помощью калькулятора конусности

  Оцените длину конуса для заготовки с большим и малым диаметрами как 12 и 6 дюймов соответственно. Возьмем угол конуса как 80,5° .
  Длина конуса рассчитывается как:

  1. Введите наружный диаметр , Dl=12 дюймD_\mathrm{l} = 12~\mathrm{дюйм}Dl​=12 дюйм.
  2. Заполните меньший диаметр , Ds=6 inD_\mathrm{s} = 6~\mathrm{in}Ds​=6 дюйм.
  3. Пластина Угол конуса 9\circ) = 11,952~\mathrm{in}
     \конец{выравнивание*}
     TPI​=2tanθ=2×tan(80,5∘)=11,952 дюйма​
     5. Далее, используя формулу длины конуса :

     Tl=Dl−DsTPI=12−60,5=0,502 in\scriptsize
     \начать{выравнивать*}
     \qquad T_\mathrm{l} &= \frac{D_\mathrm{l} — D_\mathrm{s}}{\mathrm{TPI}} \\
     &= \frac{12 — 6}{0,5} = 0,502~\mathrm{in}
     \конец{выравнивание*}
     Tl=TPIDl−Ds=0,512−6=0,502 дюйма

     Применение конусов

     Конусы широко используются для вставных адаптеров , установка сверл в патроны, держателей инструментов и самоудерживающихся круглых предметов.

     Часто задаваемые вопросы

     Что такое конус?

     Конусность представляет собой форму или профиль, один конец которого меньше другого, а поперечное сечение уменьшается постепенно.

     Как найти конусность на дюйм?

     Чтобы найти конусность на дюйм:

     1. Найдите разницу между большим и меньшим диаметрами.
     2. Разделите разницу на длину конусной области.

     Как оценить конусность на фут?

     1. Найдите разницу между большим и второстепенным диаметрами.
     2. Разделите разницу на длину конусной области.
     3. Умножьте конусность на дюйм на 12.

     Как рассчитать угол конуса?

     Угол конусности рассчитывается с помощью функции арктангенса половины конусности на дюйм.

     Рахул Дхари

     Основной диаметр (Dₗ)

     Незначительный диаметр (Dₛ)

     Длина конуса (Tₗ)

     Угол конуса (θ)

     конус (T)

     Проверьте 46 Аналогичные материалы. Расчет 🏗

     Aluminum Waisbaste. load… 43 more

     Типы конусности в механике и как рассчитать коэффициент конусности

     Прежде чем узнать типы конусности, нам нужно узнать о методах заданной конусности, чтобы мы могли хорошо понять типы конусности.

     Методы заданного конуса

     Конус можно указать следующими способами:

     • Конус в градусах
     • Конус в дюймах
     • Конус в футах
     • Конус в метрических единицах
     • Стандартный номер конуса
     • Конус по символу

     Конус в градусах

     В этом методе конусность выражается в градусах.

     Аналогично 60°, 3°, 30° и т. д.
      

     Конус в дюймах

     В дюймовых системах конусность выражается в конусности на дюйм.

     Нравится 0,0208″.

     Конус в футах

     В футовых системах конусность выражается в конусности на фут.

     Как 5/8′.

     Конус в метрической системе

     Метрические конусности представлены в соотношении 1 мм на единицу длины.

     Например, в конусе 1:20 диаметр будет изменяться на 1 мм на каждые 20 мм длины.

     Номер стандартного конуса

     В соответствии со стандартным конусом, конусность номеров может быть указана как их стандарт.
     номер

     Например, конус Морзе, указанный в MT 0
     на МТ 7.

     Конус по символу

     В этом методе конусность выражается символом, например, конусность обозначается символом
     К.

     Типы конусов

     Конусы можно разделить на три категории:

     • Согласно классу
     • Согласно использованию
     • Согласно размеру

     Согласно классу

     В зависимости от класса существует два типа конуса:

     1. Самоудерживающийся конус
     2. Быстросъемный конус

     Самоудерживающийся конус

     В этом типе конусности угол конусности
     поддерживается на уровне менее 3°.

     В этом конусе не требуется никакого другого фиксирующего устройства
     чтобы удерживать собранный компонент.

     Его также называют медленно сужающимся.

     Быстросъемный конус

     В этом типе конуса угол конуса сохраняется более
     18°.

     Из-за большого угла конусности они требуют блокировки
     приспособление для зажима.

     Коэффициент конусности 7:24.

     Согласно использованию

     В зависимости от использования есть два типа конуса

     1. Внутренний конус
     2. Внешний конус

     Внутренний конус

     Конусность, указанная на внутренней поверхности цилиндрической детали или
     заготовка называется внутренним конусом.

     Внешний конус

     Конусность, заданная на внешней поверхности цилиндрической заготовки или заготовки, равна
     называется внешней конусностью.

     В соответствии с размером

     В зависимости от размера различают следующие типы конуса:

     1. Конус Морзе
     2. Метрическая конусность
     3. Конусность Ярно
     4. Конус Брауна и Шарпа
     5. Стандартный конический штифт
     6. Конус Джейкобса

     Конус Морзе

     Конус Морзе – это самоудерживающийся конус,
     он доступен в размере 8 от MT 0 до MT 7.

     Конусность конуса Морзе составляет 1:10 и
     его включенный угол доступен в 3 ° или 5/8 дюйма / фута.

     Конус Морзе в основном используется в токарных станках с носовым шпинделем, хвостовиком сверла, оправкой,
     и т.д.

     Метрический конус

     Метрический конус представляет собой самоудерживающийся и быстросъемный конус, на котором доступны 7 размеров в самоудерживающемся исполнении и 4 размера в быстросъемном исполнении.

     Где размеры от MT O до MT 6 в самоудерживающемся типе и 30°, 40°, 45°, 50° являются быстроразъемными типами.

     Метрический конус в основном используется в токарных станках на поверхностях шпинделя.

     Ярно Конус

     Конус Ярно также является самоудерживающимся типом конуса и доступен в
     20 размеров от 01 до 20.

     Коэффициент конусности конуса Ярно – 1:20.
     и его включенный угол доступен на 0,6 дюйма / фут.

     В основном используется в машинах для маркировки штампов.

     Конус Брауна и Шарпа

     Конус Брауна и Шарпа представляет собой самоудерживающийся и быстросъемный конус, на котором доступны 18 размеров в самоудерживающемся исполнении и 09 размеров в быстросъемном исполнении.

     Где размеры от BS 1 до BS 18 самоудерживающегося типа и от 4 до 12 быстросъемного типа.

     Соотношение конусности коричневого и острого конуса составляет 1:20, а включенный угол BS 10 составляет 0,5161 дюйма/фут.

     И все другие типы конусности, включая углы, имеют размер 1/2 дюйма/фут.

     Конус Брауна и Шарпа используется в шпинделе и оправке фрезерного станка.

     Стандартный конус штифта

     Стандартный конус штифта представляет собой самоудерживающийся конус.

     Коэффициент конусности стандартной конусности штифта составляет 1:50 дюйма.
     метрическая и 1:48 в британской.

     Прилагаемый угол – 1/4 дюйма/фут.

     Стандартный конус штифта, используемый в зажимных устройствах, конический штифт и т. д.

     Конус Джейкобса

     Конус Джейкобса в основном используется в патроне сверлильного станка, оправке и т. д.

     Как рассчитать коэффициент конусности и конусность
     Угол?

     Для расчета коэффициента конусности имеются
     Следующая формула применяется:

     Соотношение конуса

     K = D-D/L

     Где,

     K = Кожурный уровень .