Сечение многогранников плоскостью. Чертеж усеченная призма
Г) призма усеченная
На рисунке 5.2 представлен комплексный чертеж прямой треугольной усеченной призмы. При построении проекций точек, лежащих на гранях призмы, необходимо выполнять условие принадлежности точки плоскости. Если задана фронтальная проекция точки К(КV), то горизонтальная ее проекция (КН) будет лежать на следе проецирующей грани ВССВ.
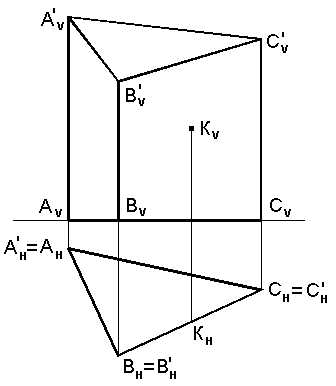
Рис. 5.2. Построение проекций точки К принадлежащей
Грани вcc’в’
Рассмотрим комплексный чертеж треугольной призмы, ребра которой произвольно наклонены к плоскостям проекций Н и V (рис. 5.3).
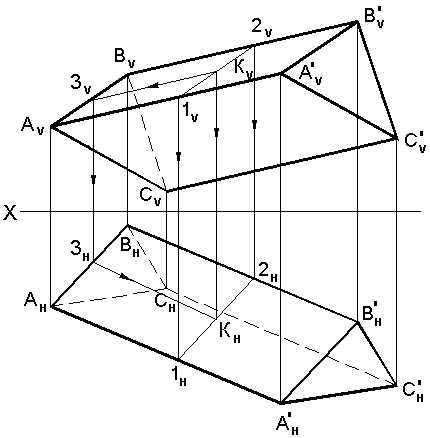
Рис. 5.3. Построение проекций точки К принадлежащей
Грани авв’а’
Требуется построить горизонтальную проекцию (КН) точки К по известной ее фронтальной проекции (КV), при условии, что точка К принадлежит грани АВВА. Выбираем в грани АВВА любую из прямых, проходящую через данную точку К. Такой прямой может быть прямая 12 произвольного положения, пересекающая ребра АА и ВВ или прямая (КЗ), параллельная боковым ребрам и пересекающая ребро АВ в точке 3. Фронтальные проекции (1V2V) и (КVЗV) прямых 12 и КЗ проходят через фронтальную проекцию (КV) искомой точки. Горизонтальные проекции (1Н2Н) и (КНЗН) определяются по условию принадлежности прямых данной грани АВВА. На пересечении линии связи с горизонтальной проекцией одной из вспомогательных прямых и будет горизонтальная проекция КН точки К.
На комплексном чертеже треугольной пирамиды SАВС рисунок 5.4 требуется построить фронтальную проекцию (КV) точки К, принадлежащей грани SBC по заданной ее горизонтальной проекции КН. Ход построения при помощи вспомогательных прямых линий (первый вариант с помощью прямой S2, второй вариант с помощью прямой К1//ВС) показан на чертеже стрелками.
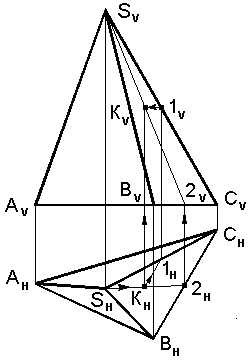
Рис. 5.4. Построение проекций точки К принадлежащей
Грани sвс
5.2. Пересечение многогранников плоскостью
Линией пересечения многогранника плоскостью в общем случае будет плоский многоугольник. Такой многоугольник может быть построен или по точкам пересечения с секущей плоскостью ребер многогранника или по линиям пересечения граней многогранника с плоскостью, т.е. задача сводится к определению точек пересечения прямой с плоскостью или к определению линий пересечения плоскостей.
Плоскую фигуру, полученную от пересечения многогранника плоскостью, называют сечением. Многоугольник сечения может вырождаться в прямые линии и точки. Число сторон многоугольника сечения равно числу граней многогранника, пересекаемых секущей плоскостью.
В зависимости от направления и положения секущей плоскости сечением куба может быть: треугольник, четырехугольник, пятиугольник и шестиугольник, как это показано на рисунке 5.5.
Если секущая плоскость будет параллельна плоскости проекций, то фигура сечения проецируется на эту плоскость проекций без искажения – в натуральную величину.
Рис. 5.5. Возможные сечения призмы
Во всех других случаях натуральный вид сечения определяется любым из способов, которые позволяют определить натуральную величину плоской фигуры.
Задача: Построить проекции и натуральную величину сечения пирамиды SABCD, пересеченной фронтально-проецирующей плоскостью Q (рис.5.6).
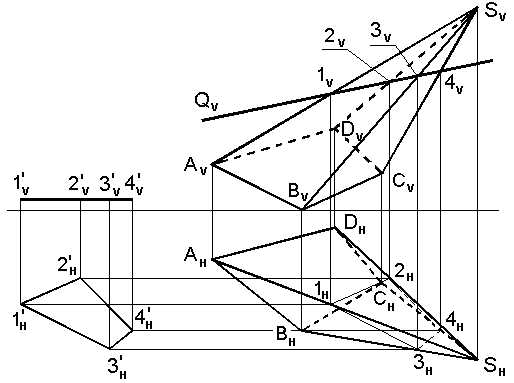
Рис. 5.6. Построение многоугольника сечения и определение его натуральной величины
Решение:
Здесь многоугольник сечения определяется по точкам пересечения ребер пирамиды с плоскостью Q.
Фронтальная проекция сечения (1V2V3V4V) вырождается в прямую линию, совпадающую со следом QV проецирующей плоскости Q. Горизонтальные проекции вершин многоугольника сечения находятся по их известным фронтальным проекциям на пересечении линий связи с соответствующими проекциями ребер пирамиды.
Фигурой сечения является многоугольник 1234, натуральная величина которого определена способом плоскопараллельного перемещения.
Если многогранник пересекается плоскостью общего положения, то для определения линии пересечения необходимо воспользоваться известными способами преобразования ортогональных проекций.
Задача: Построить проекции и натуральную величину сечения прямой треугольной призмы, стоящей на плоскости Н, плоскостью общего положения, заданной линией ската s и горизонталью h (рис.5.7).
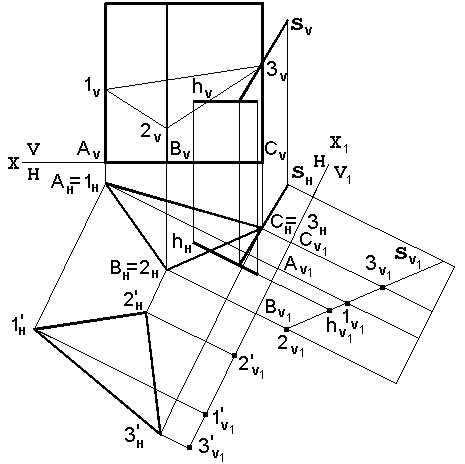
Рис. 5.7. Построение сечения призмы плоскостью общего
studfiles.net
Развертка призма. | МеханикИнфо
Развертка призмы. Развертка поверхности призмы. 4.33/5 (86.67%) проголосовало 6
Развертка боковой поверхности правильной призмы, основание которой представляет собой правильный n-угольник (в данном случае шестиугольник), высотой Н показана на рис. 1. Длина развертки равна nα и также имеет высоту Н. Основание призмы может быть присоединено к граням любой из боковых плоскостей развертки или выполнено отдельно.
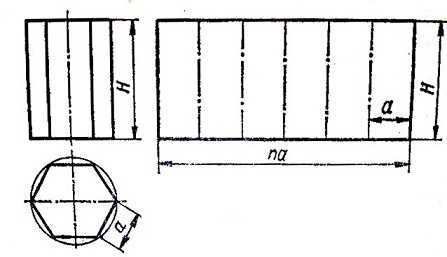
Рис 1. Развертка шестиугольной призмы.
Усеченная призма развертка.
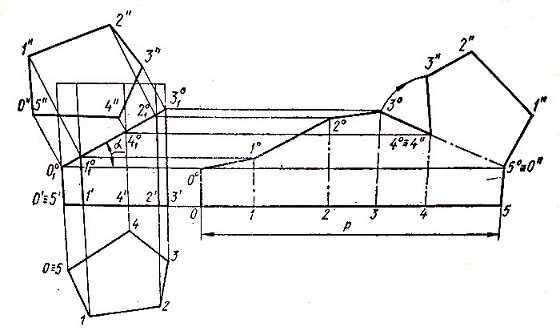
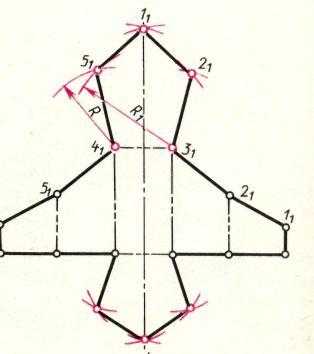
Рис. 2. Пятиугольная призма развертка усеченная плоскостью.
Из центра 1” радиусом 1°2° описывается дуга до пересечения перпендикуляра в точке 2″. Построение продолжается до замыкания многоугольника. Полученный многоугольник 0″1″2″…5″ присоединяется к какому-либо ребру развертки или выполняется отдельно.
mechanicinfo.ru
Призма
Призмой называется многогранник, у которого две грани - равные многоугольники с соответственно параллельными сторонами, а все остальные грани - параллелограммы (фиг.282,а).
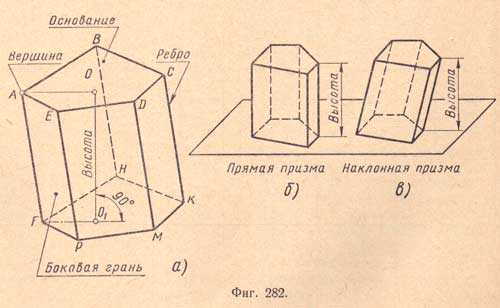
Многоугольники ABCDE и FHKMP, лежащие в параллельных плоскостях, называются основаниями призмы, перпендикуляр OO1, опущенный из любой точки основания на плоскость другого, называется высотой призмы. Параллелограммы ABHF, BCKH и т.д. называются боковыми гранями призмы, а их стороны СК, DM и т.д., соединяющие соответственные вершины оснований, - боковыми ребрами. У призмы все боковые ребра равны между собой как отрезки параллельных прямых, заключенных между параллельными плоскостями. Призма называется прямой (фиг.282,б) или наклонной (фиг.282,в) в зависимости от того, будут ли ее боковые ребра перпендикулярны или наклонны к основаниям. У прямой призмы боковые грани - прямоугольники. За высоту такой призмы можно принять боковое ребро. Прямая призма называется правильной, если ее основания - правильные многоугольники. У такой призмы все боковые грани - равные прямоугольники. Для изображения на комплексном чертеже призмы надо знать и уметь изображать элементы, из которых она состоит (точку, прямую, плоскую фигуру).Анализ элементов правильной призмы и их изображение на комплексном чертеже (фиг.283, а - и)
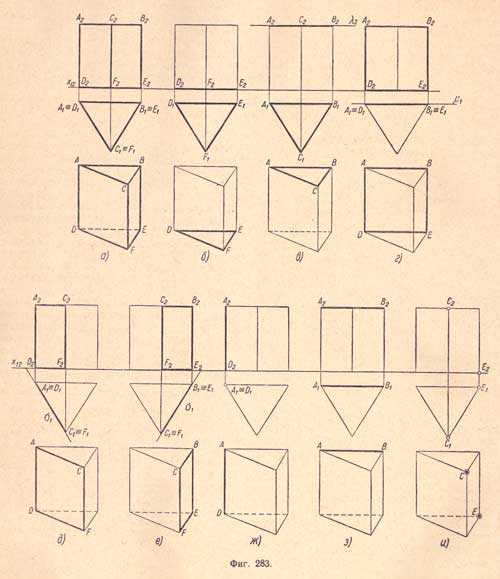
а) Комплексный чертеж призмы. Основание призмы расположено на плоскости проекций П1; одна из боковых граней призмы параллельна плоскости проекций П2.б) Ниокнее основание призмы DEF - плоская фигура - правильный треугольник, расположенный в плоскости П1; сторона треугольника DE параллельна оси х12 - Горизонтальная проекция сливается с данным основанием и, следовательно, равна его натуральной величине; фронтальная проекция сливается с осью х12 и равна стороне основания призмы.в) Верхнее основание призмы АВС - плоская фигура - треугольник, расположенный в горизонтальной плоскости. Горизонтальная проекция сливается с проекцией нижнего основания и закрывает собой ее, так как призма прямая; фронтальная проекция - прямая, параллельная оси х12, на расстоянии высоты призмы.г) Боковая грань призмы ABED - плоская фигура - прямоугольник, лежащий во фронтальной плоскости. Фронтальная проекция - прямоугольник, равный натуральной величине грани; горизонтальная проекция - прямая, равная стороне основания призмы.д) и е) Боковые грани призмы ACFD и CBEF - плоские фигуры - прямоугольники, лежащие в горизонтально - проектирующих плоскостях, расположенных под углом 60° к плоскости проекций П2. Горизонтальные проекции - прямые, расположенные к оси х12 под углом 60°, и равны натуральной величине сторон основания призмы; фронтальные проекции - прямоугольники, изображение которых меньше натуральной величины: две стороны каждого прямоугольника равны высоте призмы.ж) Ребро AD призмы - прямая, перпендикулярная к плоскости проекций П1. Горизонтальная проекция - точка; фронтальная - прямая, перпендикулярная оси х12, равная боковому ребру призмы (высоте призмы).з) Сторона АВ верхнего основания - прямая, параллельная плоскостям П1 и П2. Горизонтальная и фронтальная проекции - прямые, параллельные оси х12 и равные стороне данного основания призмы. Фронтальная проекция отстоит от оси х12 на расстоянии, равном высоте призмы.и) Вершины призмы. Точка Е - вершина нижнего основания расположена на плоскости П1. Горизонтальная проекция совпадает с самой точкой; фронтальная - лежит на оси x12.Точка С - вершина верхнего основания - расположена в пространстве. Горизонтальная проекция имеет глубину; фронтальная - высоту, равную высоте данной призмы. Отсюда следует: проектируя всякий многогранник, надо мысленно расчленить его на составные элементы и определить порядок их изображения, состоящий из последовательных графических операций. На (фиг.284 и фиг.285) приведены примеры последовательных графических операций при выполнении комплексного чертежа и наглядного изображения (аксонометрии) призм.Изображение неправильной прямой пятиугольной призмы (фиг.284).
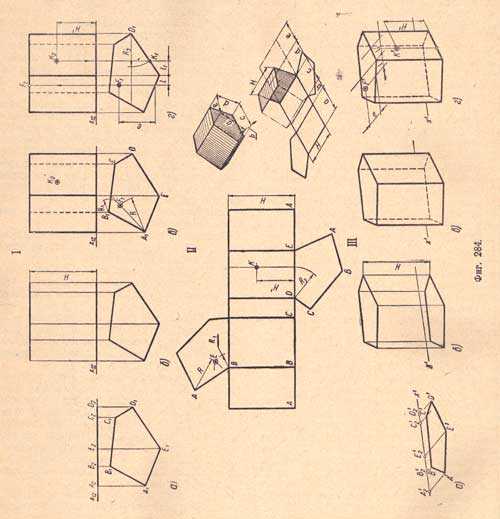
Дано: 1. Основание расположено на плоскости проекций П1.2. Ни одна из сторон основания не параллельна оси х12.I. Комплексный чертеж.I, а. Проектируем нижнее основание - многоугольник, по условию лежащий в плоскости П1.I, б. Проектируем верхнее основание - многоугольник, равный нижнему основанию с соответственно параллельными нижнему основанию сторонами, отстоящий от нижнего основания на высоту H данной призмы.I, в. Проектируем боковые ребра призмы - отрезки, расположенные параллельно; их горизонтальные проекции - точки, сливающиеся с проекциями вершин оснований; фронтальные - отрезки (параллельные), полученные от соединения прямыми одноименных проекций вершин оснований. Фронтальные проекции ребер, проведенные из проекций вершин В и С нижнего основания, изображаем штриховыми линиями, как невидимые.I, г. Даны: горизонтальная проекция F1 точки F на верхнем основании и фронтальная проекция К2 точки К на боковой грани. Требуется определить места их вторых проекций. Для точки F. Вторая (фронтальная) проекция F2 точки F будет совпадать с проекцией верхнего основания, как точка, лежащая в плоскости этого основания; ее место определяется вертикальной линией связи. Для точки К - Вторая (горизонтальная) проекция K1 точки К будет совпадать с горизонтальной проекцией боковой грани, как точка, лежащая в плоскости грани; ее место определяется вертикальной линией связи.II. Развертка поверхности призмы - плоская фигура, составленная из боковых граней - прямоугольников, у которых по две стороны равны высоте призмы, а другие две равны соответствующим сторонам основания, и из двух равных между собой оснований - неправильных многоугольников. Натуральные размеры оснований и сторон граней, необходимые для построения развертки, выявлены на проекциях; по ним и производим построение; на прямой последовательно откладываем стороны АВ, ВС, CD, DE и ЕA многоугольника - основания призмы, взятые из горизонтальной проекции. На перпендикулярах, проведенных из точек А, В, С, D, Е и А, откладываем взятую из фронтальной проекции высоту Н данной призмы и через отметки проводим прямую. В результате получаем развертку боковых граней призмы. Если к этой развертке пристроить основания призмы, получим развертку полной поверхности призмы. Основания призмы следует пристраивать к соответствующей боковой грани, пользуясь методом триангуляции. На верхнем основании призмы при помощи радиусов R и R1 определяем место точки F, а на боковой грани при помощи радиуса R3 и Н1 - точку K.III. Наглядное изображение призмы в диметрии.III, а. Изображаем нижнее основание призмы по координатам точек А, В, С, D и Е (фиг.284 I, a).III, б. Изображаем верхнее основание параллельно нижнему, отстоящее от него на высоту Н призмы.III, в. Изображаем боковые ребра, для чего соединяем прямыми соответствующие вершины оснований. Определяем видимые и невидимые элементы призмы и обводим их соответствующими линиями,III, г. Определяем на поверхности призмы точки F и К - Точку F - на верхнем основании определяем при помощи размеров i и е; точку К - на боковой грани при помощи i1 и H'. Для изометрического изображения призмы и определения мест точек F и К следует придерживаться той же последовательности.Изображение неправильной наклонной четырехугольной призмы (фиг.285).
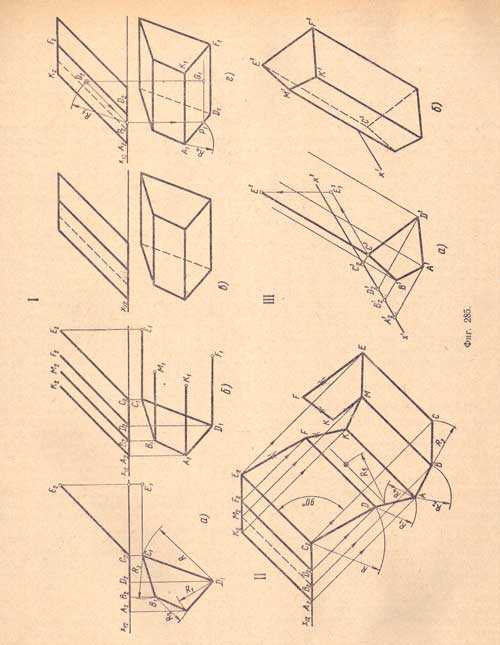
Дано:1. Основание расположено на плоскости П1.2. Боковые ребра параллельны плоскости П2. 3. Ни одна из сторон основания не параллельна оси x12I. Комплексный чертеж.I, а. Проектируем по данному условию: нижнее основание - многоугольник, лежащий в плоскости П1, и боковое ребро - отрезок, параллельный плоскости П2 и наклонный к к плоскости П1.I, б. Проектируем остальные боковые ребра - отрезки, равные и параллельные первому ребру СЕ.I, в. Проектируем верхнее основание призмы как многоугольник, равный и параллельный нижнему основанию, получаем комплексный чертеж призмы. Выявляем на проекциях невидимые элементы. Фронтальную проекцию ребра ВМ и горизонтальную проекцию стороны основания CD изображаем штриховыми линиями как невидимые.I, г. Дана фронтальная проекция Q2 точки Q на проекции A2K2F2D2 боковой грани; требуется найти ее горизонтальную проекцию. Для этого проводим через точку Q2 в проекции A2K2F2D2грани призмы вспомогательную прямую, параллельную боковым ребрам этой грани. Находим горизонтальную проекцию вспомогательной прямой и на ней при помощи вертикальной линии связи определяем место искомой горизонтальной проекции Q1 точки Q.II. Развертка поверхности призмы. Имея на горизонтальной проекции натуральные размеры сторон основания, а на фронтальной - размеры ребер, можно построить полную развертку поверхности данной призмы. Будем катить призму, повертывая ее каждый раз вокруг бокового ребра, тогда каждая боковая грань призмы на плоскости будет оставлять след (параллелограмм), равный ее натуральной величине. Построение боковой развертки будем производить в следующем порядке:а) из точек А2, В2, D2 . . . Е2 (фронтальных проекций вершин оснований) проводим вспомогательные прямые, перпендикулярные к проекциям ребер;б) радиусом R (равным стороне основания CD) делаем на вспомогательной прямой, проведенной из точки D2, засечку в точке D; соединив прямой точки С2 и D и проведя прямые, параллельные E2С2 и C2D, получим боковую грань CEFD;в) затем, аналогично пристроив следующие боковые грани, получим развертку боковых граней призмы. Для получения полной развертки поверхности данной призмы пристраиваем к соответствующим граням основания.III. Наглядное изображение призмы в изометрии.III, а. Изображаем нижнее основание призмы и ребро СЕ, пользуясь координатами согласно (фиг.284 I, a).III, б. Изображаем боковые ребра и верхнее основание. Определив невидимые ребра и стороны основания, обводим их штриховыми линиями.
Пирамида.....
www.viktoriastar.ru
Сечение многогранников плоскостью
Плоская фигура, полученная при пересечении любого многогранника плоскостью, представляет собой некоторый многоугольник. Вершины этого многоугольника находятся как точки пересечения ребер многогранника с секущей плоскостью, а стороны многоугольника строятся как линии пересечения граней многогранника с секущей плоскостью.Сечение призмы проектирующей плоскостью (фиг. 302).
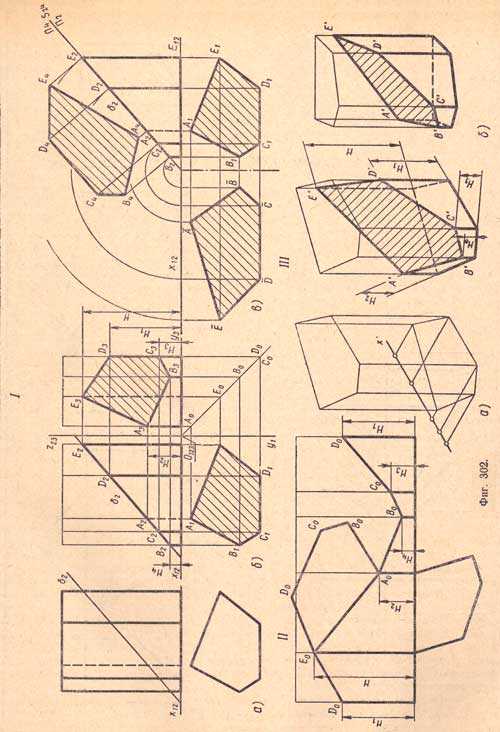
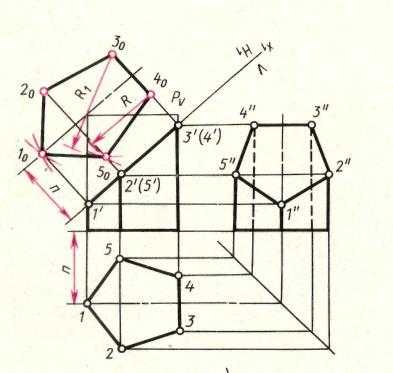
I, а. Пятиугольная прямая призма поставлена основанием на плоскость П1 и рассечена фронтально-проектирующей плоскостью δ.Требуется:а) построить проекции сечения;б) найти натуральную величину фигуры сечения;в) построить развертку поверхности усеченной призмы;г) построить аксонометрическую проекцию усеченной призмы.I, б. Нахождение проекций сечений. Фронтальная проекция В2С2А2D2Е2 фигуры сечения совпадает с фронтальной проекцией δ2 плоскости δ, так как вершины фигуры сечения являются точками пересечения ребер призмы с плоскостью δ. Горизонтальная проекция фигуры сечения совпадает с горизонтальной проекцией призмы, так как призма прямая и ее ребра и грани перпендикулярны плоскости П1. Профильная проекция фигуры сечения выявится многоугольником, полученным путем построения третьей проекции по двум данным.I, в. Нахождение натуральной величины фигуры сечения.а) Метод совмещения. Совместим плоскость δ с плоскостью П1. За ось вращения принимаем горизонтальный след плоскости δ. Проекция δ2 совместится с осью х12. Пользуясь правилом совмещения, находим натуральную величину фигуры сечения ¯A¯B¯C¯D¯E.б) Метод перемены плоскостей проекций. Принимаем плоскость δ за новую плоскость проекций, а проекцию δ2 - за новую ось проекций s24. Проводим из проекций B2C2A2D2 и Е2 перпендикуляры к новой оси s24 и на них откладываем глубины вершин фигуры сечения, например: E2E4 = E1E4 и т.д. Точки A4, B4, С4, D4, E4 последовательно соединяем прямыми и получаем натуральную величину фигуры сечения. Фигуру сечения и ее проекции на чертеже выделяют штриховкой под углом 45° к оси х12. Штриховка может быть наклонена как вправо, так и влево, но для всех проекций и фигуры сечения штриховку следует выполнять в одну сторону.II. Построение развертки поверхности усеченной призмы. Строим развертку боковой поверхности данной призмы. Затем на соответствующих боковых ребрах откладываем размеры оставшихся после отсечения плоскостью частей ребер H, Н1, Н2, h4 и Н4, которые берем с фронтальной и профильной проекций. Соединив последовательно прямыми точки DO, ЕO, АO, ВO, СO, DO, получим линию сечения, по которой плоскость δ рассекает призму на две части. Для получения развертки поверхности усеченной призмы к соответствующим боковым граням пристраиваем фигуру сечения и нижнее основание.III. Построение аксонометрических проекций усеченной призмы.III, а. Строим аксонометрическую проекцию призмы, пользуясь координатами на (фиг.302, I, а).III, б. На соответствующих ребрах боковых граней откладываем от нижнего основания оставшиеся части ребер, используя для этого размеры Н, Н1, Н3, Н3, h5. Полученные точки А', В', С, D', Е' и А' соединяем прямыми. Определяем невидимые и видимые элементы и обводим их соответствующими линиями.Сечение призмы плоскостью общего положения (фиг.303).
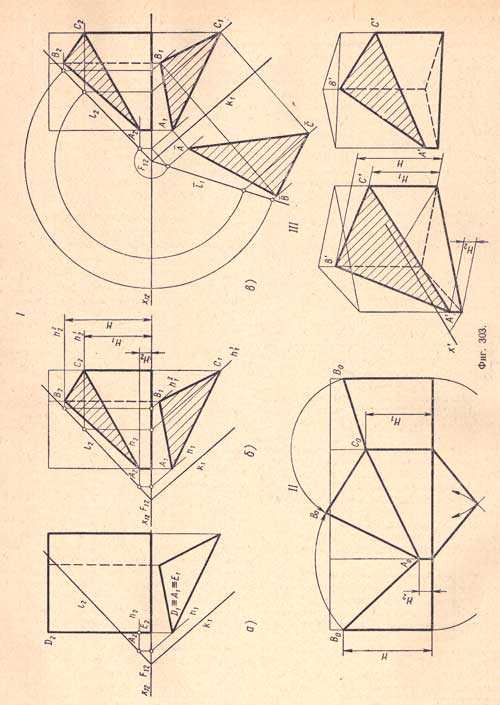
I, а. Треугольная прямая призма поставлена основанием на плоскость П1 и рассечена плоскостью а общего положения.Требуется: а) построить проекции сечения;б) найти натуральную величину фигуры сечения;в) построить развертку поверхности усеченной призмы;г) построить аксонометрическую проекцию усеченной призмы. В этом случае горизонтальная проекция фигуры сечения сливается с горизонтальной проекцией призмы, так как боковые ребра и грани призмы перпендикулярны плоскости П1. Для построения фронтальной проекции воспользуемся горизонталями. Через точку А1 - горизонтальную проекцию ребра - проводим прямую, параллельную проекции следа k1 - горизонтальную проекцию h2 горизонтали. Затем найдем ее фронтальную проекцию h3, которая, пересекаясь с фронтальной проекцией ребра D2E2 в точке А2 определит фронтальную проекцию точки пересечения ребра призмы с плоскостью а.I, б. Аналогичным построением находим остальные точки пересечения ребер призмы плоскостью а (В2, С2), после чего соединим последовательно прямыми точки А2, В2, С2 и А2 и получим фронтальную проекцию А2В2С2 фигуры сечения - треугольника.I, в. Натуральную величину фигуры сечения находим путем совмещения плоскости а с плоскостью П1 вращением вокруг проекции следа k1II и III. Построение развертки поверхности усеченной призмы и аксонометрических проекций аналогично соответствующим построениям для пятиугольной призмы (фиг.302).Сечение пирамиды фронтально - проектирующей плоскостью (фиг. 304).
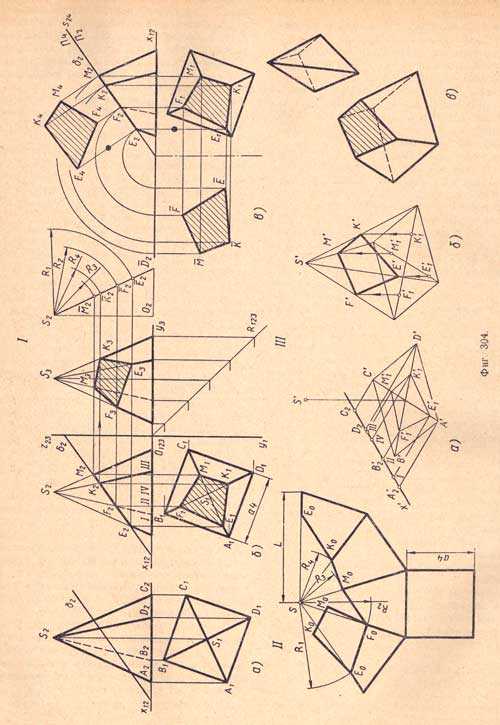
1, а. Правильная четырехугольная пирамида поставлена основанием на плоскость П1 и рассечена фронтально-проектирующей плоскостью б.Требуется:а) построить проекции сечения;б) найти натуральную величину фигуры сечения;в) построить развертку поверхности усеченной пирамиды;г) построить аксонометрическую проекцию усеченной пирамиды (фиг.304, а).I. б. Фронтальная проекция фигуры сечения - отрезок E2F2К2М2 - совпадает с фронтальной проекцией δ2 так как точки пересечения ребер пирамиды с секущей плоскостью лежат в плоскости δ. Горизонтальные проекции точек пересечения находят при помощи вертикальных линий связи на горизонтальных проекциях соответствующих ребер, например: точку Е1 на горизонтальной проекции ребра S1A1, точку F1на S1B1 и т.д. Соединив последовательно прямыми точки Къ Ei, &i, JWi и Кг, получим горизонтальную проекцию фигуры сечения. Профильная проекция фигуры сечения - четырехугольник E3F3M3K3 находится, как третья проекция, по двум данным (фиг.304,б).I. в. Натуральная величина фигуры сечения находится способом совмещения плоскости δ с плоскостью П1 и способом перемены плоскостей проекций, где за новую плоскость П4 принята плоскость δ, а за новую ось проекций S24 - проекция δ2 (фиг.304,в).II. Для построения развертки боковой поверхности находим натуральную величину ребра пирамиды путем построения прямоугольного треугольника S2O2¯D2, у которого S2O2 = H, a O2¯D2 = S1¯D1; гипотенуза S2D2 является натуральной величиной ребра. Зто равносильно повороту ребра до параллельности плоскости П2. Затем строим развертку боковой поверхности нерассеченной пирамиды - фигуру, состоящую из четырех равнобедренных треугольников, основания которых равны сторонам квадрата основания, а боковые стороны - натуральным величинам ребер. Для определения величины отсеченных частей ребер, вместо поворота их, переносим с профильной проекции на натуральную величину ребра точки E3,F3,M3 и К3, получаем размеры R1,R2,R3,R4 Равные отсеченным частям ребер размер R1 равен отсеченной части S2¯E2, R2 равен S2¯F2 и т. д. (фиг.304, I, б). Перенеся на развертку при помощи этих размеров на соответствующие ребра точки Ео, Fo, Мо, Ко и Ео и соединив их последовательно прямыми, получим ломаную линию, по которой пирамида рассечена фронтально-проектирующей плоскостью δ. Для получения развертки поверхности усеченной пирамиды к линии сечения присоединяем соответствующей стороной фигуру сечения, а к линии основания — основание пирамиды.III, а. Для изображения изометрической проекции усеченной пирамиды, пользуясь координатами с (фиг.304, I, б), сначала строим основание и вершину пирамиды, а затем вторичную проекцию фигуры сечения (горизонтальную проекцию фигуры сечения) E'1F'1M'1K'1.III, б. Соединяем прямыми точку S' (вершину пирамиды) с точками А', В', С и D' (вершинами основания) - получаем изометрическую проекцию пирамиды. Из точек Е'1, F'1, M'1 и К'1 параллельно оси z проводим прямые до пересечения с соответствующими ребрами пирамиды. Точки Е'1, F'1, M'1 и К'1 явятся вершинами фигуры сечения, соединив которые прямыми, получим изометрическую проекцию фигуры сечения.III, в. Определив видимые и невидимые элементы усеченной призмы, обводим их соответствующими линиями и заштриховываем фигуру сечения. Над усеченной частью пирамиды изображена отсеченная ее часть.
Сечение тел вращения плоскостью.....
www.viktoriastar.ru
Пересечение многогранника с прямой
При пересечении многогранника с прямой получаем две точки (точку входа и точку выхода).
Для их нахождения необходимо:
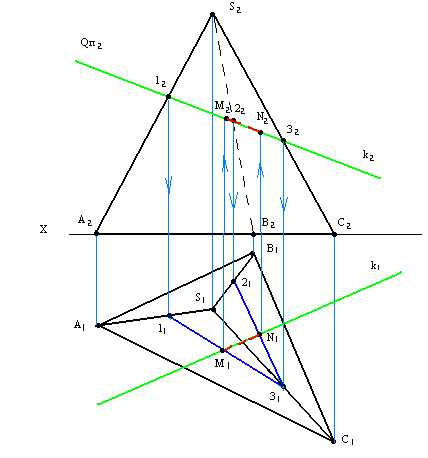
1.Через данную прямую провести проецирующую вспомогательную плоскость Qп2.
2.Находим сечение многогранника вспомогательной проецирующей плоскостью
3.Определяем точки пересечения данной прямой с сечением – это и есть искомые точки.
Часть прямой внутри многогранника невидимая.
Изображение тел вращения на комплексном чертеже
1
1 1
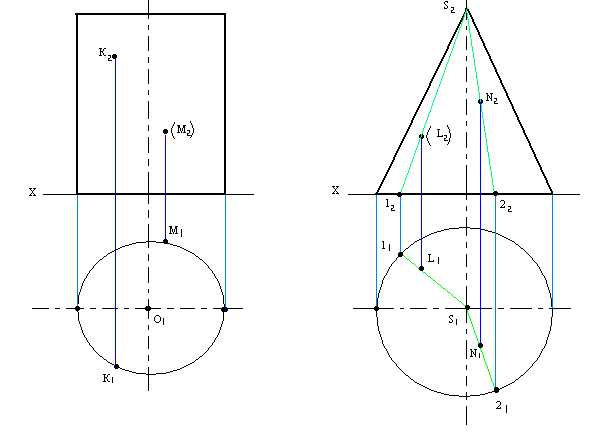
Чтобы на конусепостроитьL1иN1 следует связать точки с основанием при помощи какой-либо прямой:
1.Связываем L2прямой 12S2иN2прямой 22S2
2.Строим 11S1и 21S1
3.Находим L1иN1
2
1
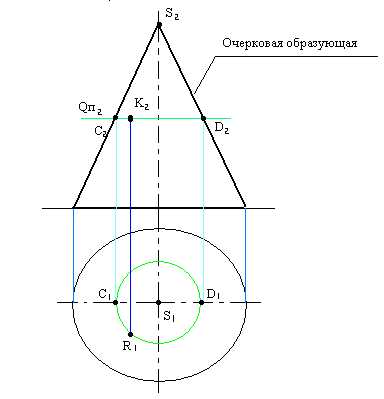
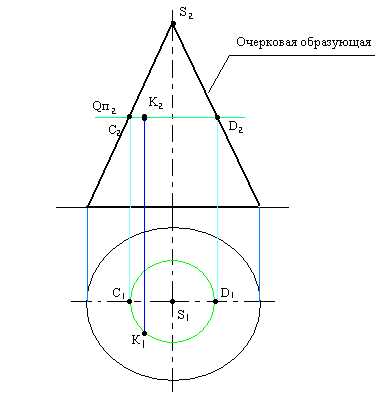
Через К2проводим горизонтальную секущую плоскостьQп2. В сечении конуса получается окружность ø С2D2. Строим на П1горизонтальную проекцию сечения – окружность ø С2D2. На этой окружности по линии связи находим К12
Сечение тела вращения проецирующей плоскостью
Определение НВ сечения
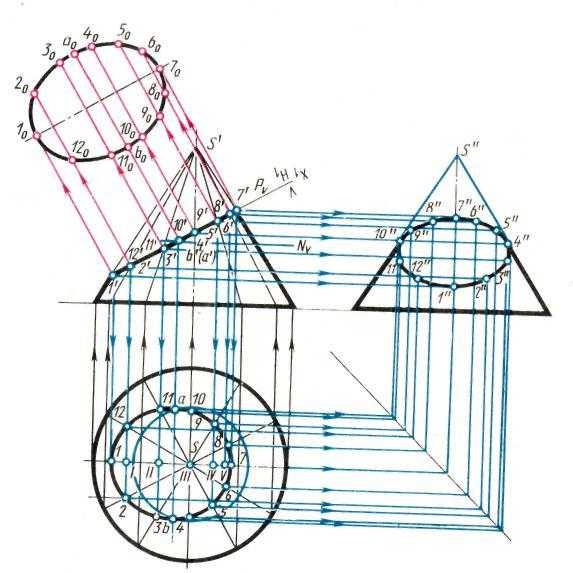
Методом перемены плоскостей проекций
.
Вопросы для самопроверки
Как изобразить на комплексном чертеже пирамиду?
Как изобразить на комплексном чертеже призму?
Как определить проекции точки принадлежащей грани многогранника?
Определить точки пересечения прямой с гранями многогранника?
Как изобразить на комплексном чертеже проекции цилиндра?
Как изобразить на комплексном чертеже проекции конуса?
Как изобразить на комплексном чертеже проекции сферы?
Как изобразить на комплексном чертеже проекции тора?
Тема: построение развёрток поверхностей
Развёрткой называется плоская фигура, полученная при совмещении поверхности геометрического тела с одной плоскостью (без наложения граней или иных элементов поверхности друг на друга.)
Развертка усеченной призмы
| | |
Развертку боковой поверхности с основанием и фигурой сечения призмы строят следующим образом. Проводят прямую, на которой откладывают пять отрезков, равных длинам сторон пятиугольника, лежащего в основании призмы. Из полученных точек проводят перпендикуляры, на которых откладывают действительные длины ребер усеченной призмы, беря их с фронтальной или профильной проекции, получают развертку боковой поверхности призмы.
К развертке боковой поверхности пристраивают фигуру нижнего основания — пятиугольник и фигуру сечения. При этом используют метод триангуляции (метод засечек). На рисунке показано построение вершины 5 методом триангуляции. Линии сгиба по ГОСТ 2.303—68 показывают на развертке штрих-пунктирной линией с двумя точками.
Развертка усеченного цилиндра
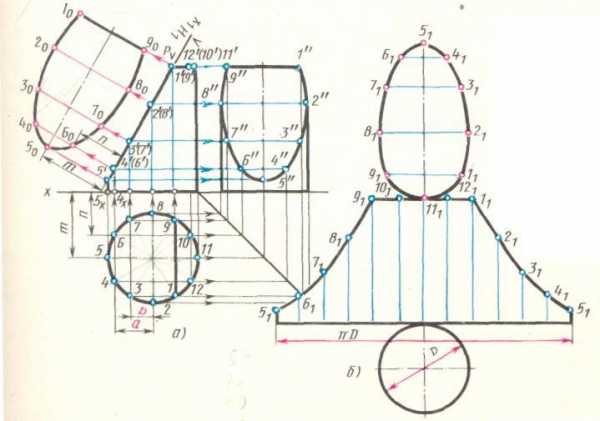Для построения развертки на горизонтальной прямой откладывают длину окружности основания, равную ПD, и делят ее на 12 равных частей. Из точек деления восставляют перпендикуляры к отрезку ПD, на них откладывают действительные длины образующих цилиндра от основания до секущей плоскости Р, которые взяты с фронтальной или профильной проекции цилиндра. Полученные точки 11... 9 1 соединяют по лекалу плавной кривой. Затем фигуру сечения соединяют с частью верхнего основания цилиндра, ограниченного хордой 1191 (сегмент), а фигуру нижнего основания цилиндра (окружность) соединяют с нижней частью развертки.
studfiles.net
Как сделать призму из бумаги?
В основе геометрического тела – призмы лежат многоугольники, а каждая боковая грань – параллелограмм. Непосвященный, возможно, немного испугался. Но если вашего ребенка просят прийти на урок с призмой, вы, естественно, захотите помочь ему и объяснить, как сделать призму из бумаги.
Начнем с изготовления прямой призмы. В этой призме боковые ребра перпендикулярны основаниям. Наиболее проста в изготовлении своими руками призма из бумаги с тремя гранями, так как в ее основаниях лежат простейшие из многоугольников – треугольники. Изготовим «правильную» призму. У нее основания представлены равносторонними треугольниками.
Треугольная призмаПродумаем, какая по высоте будет наша треугольная призма из бумаги. Начертим прямоугольник-с одной стороной, равной высоте, а другой - равной длине периметру треугольника в основании. Полученный прямоугольник разделим параллельными прямыми на три равные части. От углов прямоугольника, находящегося в середине, циркулем проведем окружности с радиусом, равным стороне нашего треугольника в основании. Где окружности пересекутся за пределами первоначального прямоугольника, поставим точки и соединим их с центрами окружностей. Мы должны получить фигуру, изображенную в середине рисунка.
Далее фигуру вырезаем с небольшими припусками для склеивания, сгибаем по имеющимся прямым линиям и получаем готовую призму.По какому шаблону изготавливается призма из бумаги с четырьмя гранями, наглядно демонстрирует схема на рисунке.
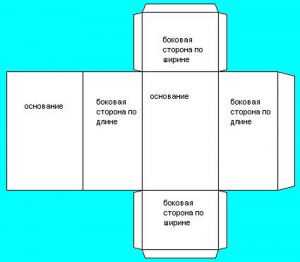Шестиугольная призма Пример заготовки для пятигранной призмы представлен на рисунке.
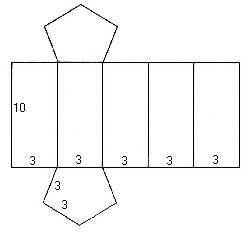Здесь высота пирамиды 10 см, длина сторон у пятигранника в основании по 3 см. Похожим образом может быть изготовлена шестиугольная призма из бумаги, но в ее основании лежит шестиугольник. Наклонная призма Наклонная призма из бумаги представлена на этом рисунке.
Ее боковые грани находятся под углом к основанию. Такую призму можно изготовить по шаблону-развертке. Освоив изготовление призмы, можно приступать к следующим геометрическим фигурами: пирамиде, параллелепипеду и более сложному икосаэдру из бумаги.
womanadvice.ru
Комплексный чертеж призмы | Класс
- Кулагина Татьяна Николаевна, учитель черчения
Разделы: Технология
Цели и задачи уроки.
Оборудование:
- модели геометрических тел,
- шаблоны для построения 6-и угольника в изометрии,
- развертка 6-и угольной призмы,
- чертежные инструменты и принадлежности.
План занятия.
Лекционная часть.
2.1. Многогранники2.2. Сечение многогранников
Практическая часть.
2.3. Построение 6-угольной призмы с сечением фронтально-проецирующей плоскостью.2.4. Построение развертки усеченной призмы.
Ход занятия
1. Вопросы для повторения:
Какие бывают прямые и плоскости?
— Общего и частного положения.
Как располагаются в пространстве проецирующие прямые и проецирующие плоскости?
— Они перпендикулярны плоскостям проекций.
Назовите способы преобразования чертежа.
— Способ вращения, способ перемены плоскостей проекций.
Когда применяется способ перемены плоскостей проекций?
— Когда требуется определить натуральную величину наклонного сечения для построения развертки геометрического тела.
2. Записываем новую тему “Многогранники”.
Форма многих технических деталей представляет собой сочетание простых геометрических тел. Поэтому для выполнения чертежей изделий необходимо знать, как правильно изображаются различные геометрические тела. Рассмотрим построение на комплексном чертеже основных геометрических тел: призмы, пирамиды, цилиндра, конуса, сферы, тора.
Призма.
Призмой называется многогранник, у которого 2 грани (основания) — равные многоугольники с соответственно параллельными сторонами, а боковые грани – прямоугольники (у прямой призмы) или параллелограммы (у наклонной). Мы рассмотрим прямую призму. Элементы призмы: вершины, ребра (боковые и основания), грани (2 основания и боковые).
Рассмотрим 3 проекции 6-угольной призмы. На главном виде – это прямоугольники, боковые ребра – это горизонтально проецирующие прямые, 6-угольник на виде сверху представляет собой проекцию обоих оснований.
Сечение призмы выполнено фронтально-проецирующей плоскостью.
Сечение поверхности геометрических тел плоскостью называется плоская фигура, точки которой принадлежат и поверхности тела, и секущей плоскости. Сечение широко применяется в техническом черчении для выявления формы и внутреннего устройства предметов. В сечении многогранника плоскостью образуется многоугольник. Вершины многоугольника – это точки пересечения ребер многогранника с секущей плоскостью, стороны – это линии пересечения секущей плоскости с гранями многогранника.
Задача на построение комплексного чертежа усеченного многогранника состоит из решения следующих вопросов:
Рассмотрим все поставленные задачи.
Задача 1. (см. Рис. 1).
Для построения трех проекций усеченной призмы выполняем следующие операции:
Задача 2. (см. Рис. 1).
Решение задачи 2 проводится с использованием чертежа, полученного при решении задачи 1. Для определения натуральной величины сечения используем метод вспомогательных секущих плоскостей. Для решения задачи выполняем следующие операции:
Задача 3. (см. Рис. 2).
Разверткой (выкройкой) поверхности тела называется плоская фигура, полученная путем совмещения всех точек данной поверхности с плоскостью без разрывов и складок.
Построение разверток выполняется обычно графическими приемами, с применением способов, предлагаемых начертательной геометрией. Построение развертки поверхности многогранника сводится к определению истинной величины каждой его грани по чертежу многогранника (см. Рис. 1). После этого грани многогранника стыкуются (соединяются) по ребрам и вершинам.
Для решения задачи 3 выполняем следующие операции:
Проводим горизонтальную прямую, на которой от произвольно выбранной точки А, откладываем отрезки AB, BC, CD, DE, EF, FA, равные длине стороны основания а = 30.
Из точек A, B, C, D, E, F, A восстанавливаем перпендикуляры и на них откладываем величины ребер усеченной призмы. Величины данных отрезков A1, B2, C3, D4, E5, F6, A1 берем с фронтальной проекции усеченной призмы. Полученные точки соединяем и получаем развертку боковой поверхности призмы.
К одному из отрезков основания, например к BC, пристраиваем 6-угольник ABCDEF.
К одному из звеньев ломаной, например, к отрезку 2-3, пристраиваем 6-угольник 123456 (сечение призмы), который переносим, используя метод засечек, с рисунка 1.
Рис 1
Рис 2
Задача 4. (см. рис. 3)
Строим усеченную 6-и угольную призму в изометрии. Сторона основания призмы, а = 30. Для выполнения задачи учащимся раздаются трафареты 6-и угольника в изометрии. Высоты A1, B2, C3, D4, E5, F6 – берем с фронтальной проекции усеченной призмы.
class.chernykh.net
