Прямоугольная диметрическая проекция. Косоугольная фронтальная диметрическая проекция
Аксонометрические проекции | CADInstructor
Во многих случаях при выполнении технических чертежей оказывается полезным наряду изображением предметов в системе ортогональных проекций иметь более наглядные изображения. Для построения таких изображений применяются проекции, называемые аксонометрическими.
Способ аксонометрического проецирования состоит в том, что данный предмет вместе с осями прямоугольных координат, к которым эта система относится в пространстве, параллельно проецируется на некоторую плоскость α (Рисунок 4.1).
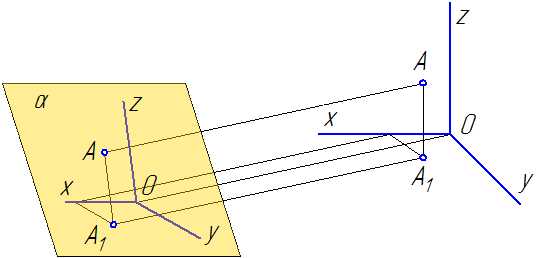
Рисунок 4.1
Направление проецирования S определяет положение аксонометрических осей на плоскости проекций α, а также коэффициенты искажения по ним. При этом необходимо обеспечить наглядность изображения и возможность производить определения положений и размеров предмета.
В качестве примера на Рисунке 4.2 показано построение аксонометрической проекции точки А по ее ортогональным проекциям.
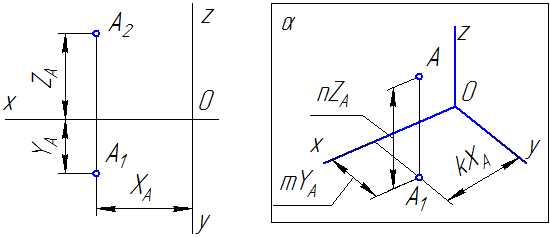
Рисунок 4.2
Здесь буквами k, m, n обозначены коэффициенты искажения по осям OX, OY и OZ соответственно. Если все три коэффициента равны между собой, то аксонометрическая проекция называется изометрической, если равны между собой только два коэффициента, то проекция называется диметрической, если же k≠m≠n, то проекция называется триметрической.
Если направление проецирования S перпендикулярно плоскости проекций α, то аксонометрическая проекция носит названия прямоугольной. В противном случае, аксонометрическая проекция называется косоугольной.
ГОСТ 2.317-2011 устанавливает следующие прямоугольные и косоугольные аксонометрические проекции:
- прямоугольные изометрические и диметрические;
- косоугольные фронтально изометрические, горизонтально изометрические и фронтально диметрические;
Ниже приводятся параметры только трех наиболее часто применяемых на практике аксонометрических проекций.
Каждая такая проекция определяется положением осей, коэффициентами искажения по ним, размерами и направлениями осей эллипсов, расположенных в плоскостях, параллельных координатным плоскостям. Для упрощения геометрических построений коэффициенты искажения по осям, как правило, округляются.
4.1. Прямоугольные проекции
4.1.1. Изометрическая проекция
Направление аксонометрических осей приведено на Рисунке 4.3.
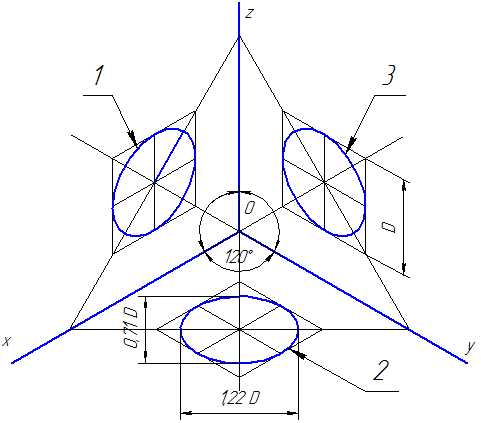
Рисунок 4.3 – Аксонометрические оси в прямоугольной изометрической проекции
Действительные коэффициенты искажения по осям OX, OY и OZ равны 0,82. Но с такими значениями коэффициентов искажения работать не удобно, поэтому, на практике, используются приведенные коэффициенты искажений. Эта проекция обычно выполняется без искажения, поэтому, приведенные коэффициенты искажений принимается k = m = n =1. Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются в эллипсы, большая ось которых равна 1,22, а малая – 0,71 диаметра образующей окружности D.
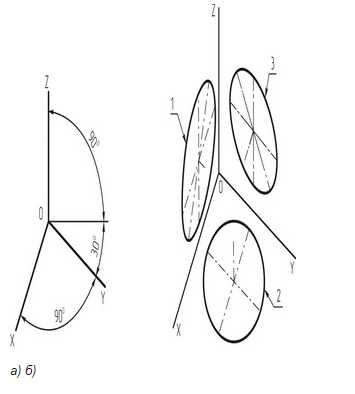
Большие оси эллипсов 1, 2 и 3 расположены под углом 90º к осям OY, OZ и OX, соответственно.
Пример выполнения изометрической проекции условной детали с вырезом приводится на Рисунке 4.4.
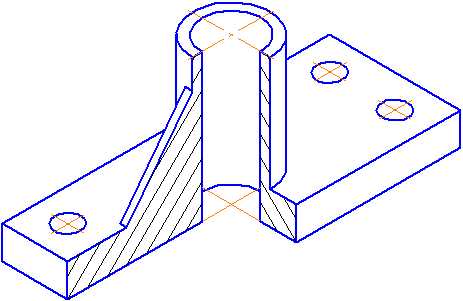
Рисунок 4.4 – Изображение детали в прямоугольной изометрической проекции
4.1.2. Диметрическая проекция
Положение аксонометрических осей проводится на Рисунке 4.5.
Для построения угла, приблизительно равного 7º10´, строится прямоугольный треугольник, катеты которого составляют одну и восемь единиц длины; для построения угла, приблизительно равного 41º25´ — катеты треугольника, соответственно, равны семи и восьми единицам длины.
Коэффициенты искажения по осям ОХ и OZ k=n=0,94 а по оси OY – m=0,47. При округлении этих параметров принимается k=n=1 и m=0,5. В этом случае размеры осей эллипсов будут: большая ось эллипса 1 равна 0,95D и эллипсов 2 и 3 – 0,35D (D – диаметр окружности). На Рисунке 4.5 большие оси эллипсов 1, 2 и 3 расположены под углом 90º к осям OY, OZ и OX, соответственно.
Пример прямоугольной диметрической проекции условной детали с вырезом приводится на Рисунке 4.6.
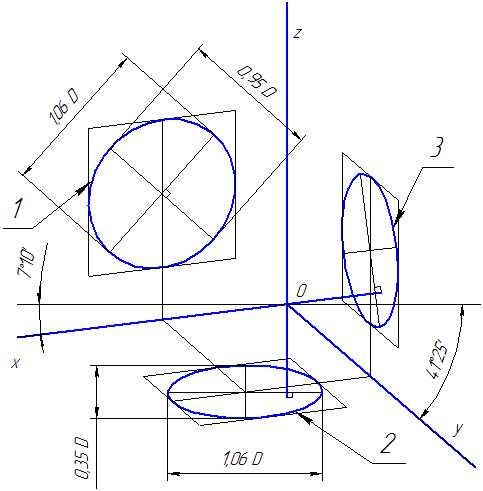
Рисунок 4.5 – Аксонометрические оси в прямоугольной диметрической проекции
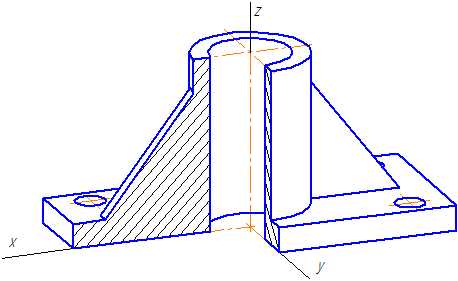
Рисунок 4.6 – Изображение детали в прямоугольной диметрической проекции
4.2 Косоугольные проекции
4.2.1 Фронтальная диметрическая проекция
Положение аксонометрических осей приведено на Рисунке 4.7. Допускается применять фронтальные диметрические проекции с углом наклона к оси OY, равным 300 и 600.
Коэффициент искажения по оси OY равен m=0,5 а по осям OX и OZ — k=n=1.
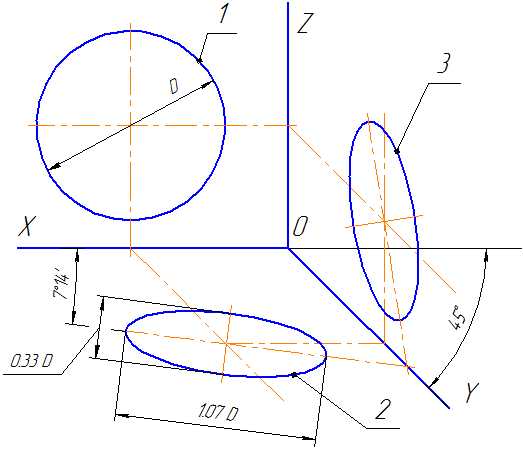
Рисунок 4.7 – Аксонометрические оси в косоугольной фронтальной диметрической проекции
Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на плоскость XOZ без искажения. Большие оси эллипсов 2 и 3 равны 1,07D, а малая ось – 0,33D (D — диаметр окружности). Большая ось эллипса 2 составляет с осью ОХ угол 7º 14´, а большая ось эллипса 3 составляет такой же угол с осью OZ.
Пример аксонометрической проекции условной детали с вырезом приводится на Рисунке 4.8.
Как видно из рисунка, данная деталь располагается таким образом, чтобы её окружности проецировались на плоскость XОZ без искажения.
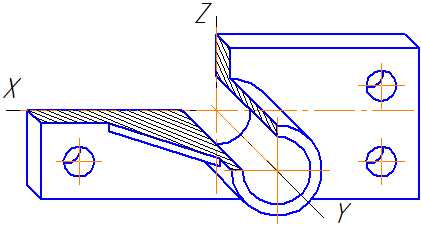
Рисунок 4.8 – Изображение детали в косоугольной фронтальной диметрической проекции
4.3 Построение эллипса
4.3.1 Построения эллипса по двум осям
На данных осях эллипса АВ и СD строятся как на диаметрах две концентрические окружности (Рисунок 4.9, а).
Одна из этих окружностей делится на несколько равных (или неравных) частей.
Через точки деления и центр эллипса проводятся радиусы, которые делят также вторую окружность. Затем через точки деления большой окружности проводятся прямые, параллельные линии АВ.
Точки пересечения соответствующих прямых и будут точками, принадлежащими эллипсу. На Рисунке 4.9, а показана лишь одна искомая точка 1.
а б в
Рисунок 4.9 – Построение эллипса по двум осям (а), по хордам (б)
4.3.2 Построение эллипса по хордам
Диаметр окружности АВ делится на несколько равных частей, на рисунке 4.9,б их 4. Через точки 1-3 проводятся хорды параллельно диаметру CD. В любой аксонометрической проекции (например, в косоугольной диметрической) изображаются эти же диаметры с учетом коэффициента искажения. Так на Рисунке 4.9,б А1В1=АВ и С1 D1 = 0,5CD. Диаметр А 1В1 делится на то же число равных частей, что и диаметр АВ, через полученные точки 1-3 проводятся отрезки, равные соответственным хордам, умноженным на коэффициент искажение (в нашем случае – 0,5).
4.4 Штриховка сечений
Линии штриховки сечений (разрезов) в аксонометрических проекциях наносятся параллельно одной из диагоналей квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям (Рисунок 4.10: а – штриховка в прямоугольной изометрии; б – штриховка в косоугольной фронтальной диметрии).
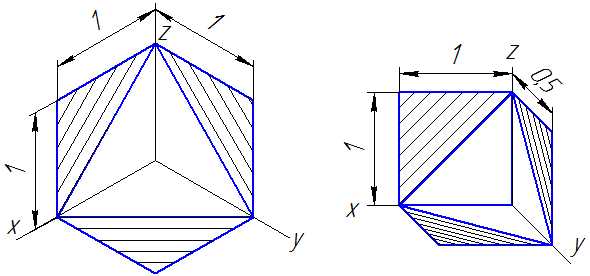
а бРисунок 4.10 – Примеры штриховки в аксонометрических проекциях
cadinstructor.org
Прямоугольная диметрическая проекция
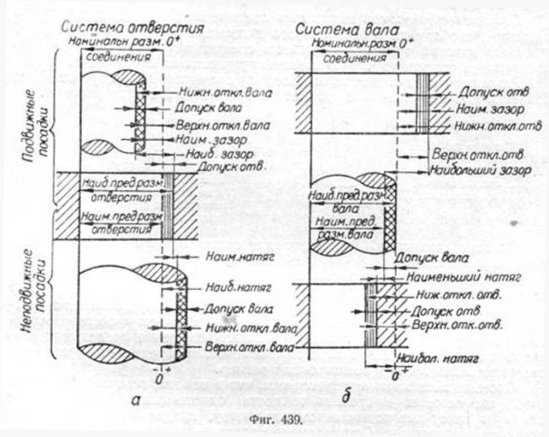
В прямоугольной диметрической проекции аксонометрические оси Ooxo иOozo составляют между собой угол 97о10’. ОсьOoyo является биссектрисой оставшегося угла, составляя с двумя другими осями равные углы 131о25’ (рис. 11). При построении этой проекции принимают, что
Kx=KzиKy= 0,5Kx.
Тогда по основной теореме аксонометрии получаем из формулы
K2x+ K2y + K2z = 2, что 2K2x+ (0,5Kx)2 = 2,
тогда K2x= 8/9;Kx= 0,94.
Приведенные коэффициенты искажения будут равны:
Kx= Kz = 1; Ky = 0,5,
что соответствует увеличению изображения в 1,06 раза (1/0,94 = 1,06).
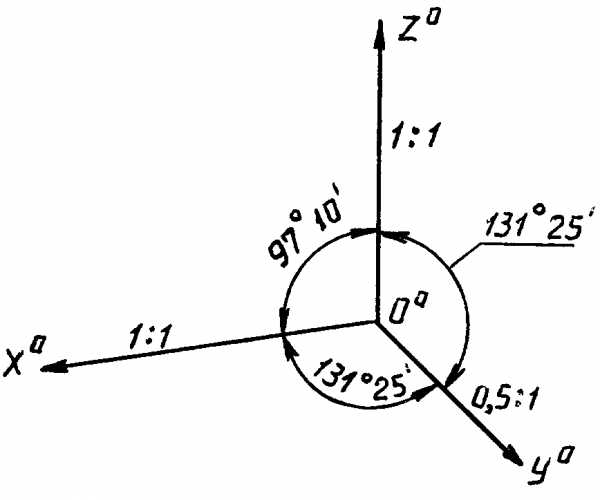
Рис. 11
Прямоугольная диметрия рекомендуется к применению в случае, когда наибольшее число характерных особенностей сосредоточено на одной стороне предмета. Наиболее отличающаяся особенностями сторона предмета располагается параллельно плоскости XoOoZo.Косоугольная фронтальная диметрическая проекция
Аксонометрическая плоскость располагается параллельно фронтальной плоскости проекций V (рис. 12). Поэтому аксонометрические осиOoxo иOozo параллельны декартовым осямOxиOz. Соответственно, коэффициенты искаженияKx=Kz. ЗначениеKyпринимается равным 0,5. Расположение аксонометрических осей показано на рисунке .
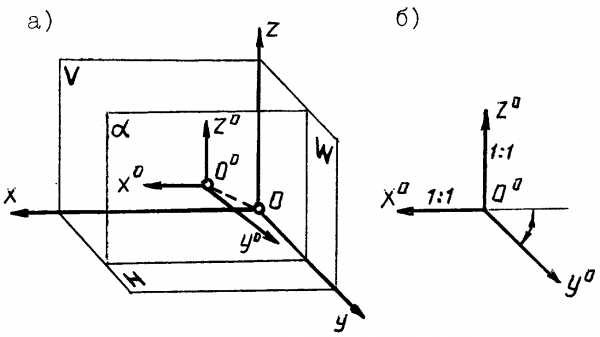
Рис. 12
Косоугольная фронтальная диметрия удобна в тех случаях, когда изображаемая геометрическая фигура содержит большое число окружностей (или других кривых, состоящих из дуг окружностей), лежащих на взаимно параллельных плоскостях. При расположении этих плоскостей параллельно аксонометрической плоскости, все окружности будут проецироваться на ней также в виде окружностей, что упрощает построение.Комплексный чертеж точки и прямой
План:
3.1. Комплексный чертеж точки
3.2. Проекции прямых общего положения
3.3. Проекции прямых уровня
Горизонталь - прямая равных высот
Фронталь - прямая равных глубин
Профильная прямая - прямая равных широт
3.4. Проекции проецирующих прямых
Горизонтально-проецирующая прямая
Фронтально-проецирующая прямая
Профильно-проецирующая прямая
3.5. Определение натуральной величины отрезка прямой общего положения
3.6. Деление отрезка прямой в данном отношени
Комплексный чертеж точки
Внутри трехгранного угла, образованного горизонтальной (H), фронтальной (V) и профильной (W) плоскостями проекций, расположим какую-либо точку А (рис. 13).
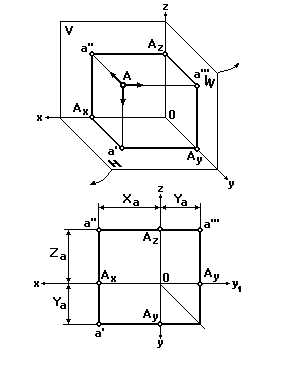
Рис. 13
Направим проецирующий луч перпендикулярно плоскости V. Точка пересечения этого луча с плоскостью V будет фронтальной проекцией a'' точкиA. Спроецируем точку А на плоскость H и получим ее горизонтальную проекциюa'. Проецируя точку А на плоскость W, получим ее профильную проекциюa'''.Для получения чертежа необходимо все три плоскости V, H и W вместе с построенными на них проекциями совместить в одну плоскость, т.е. развернуть их.
При этом плоскость H поворачивается вокруг оси xна 90 градусов книзу, плоскость W — вокруг осиzна 90 градусов вправо, а плоскость V остается неподвижной (при этом осьyкак бы раздваивается).
В результате совмещения получают чертеж точки в трех проекциях. Очертания плоскостей H, V и W на чертеже не показывают.
Линию, связывающую горизонтальную и профильную проекции точки А, представляют двумя отрезками ломаной линии. Вершина ее лежит на биссектрисе угла, образованного осями yиy1. Эту биссектрису называютпостоянной линией чертежа.
Прямые линии, соединяющие проекции точки и перпендикулярные осям проекций, называют линиями проекционной связи(рис. ).
Координатный отрезок, равный превышению точки А над плоскостью H, называют высотойZa(аппликатой) точки А. Координатный отрезок, равный расстоянию от точки А до плоскости V, называютглубинойYa(ординатой) точки А. Координатный отрезок, равный расстоянию от точки А до плоскости W, называютширотойXa(абсциссой) точки А.
Горизонтальная проекция точки А определяется на эпюре ее координатами XaиYa, а фронтальная — координатамиXaиZa(рис. 13).
studfiles.net
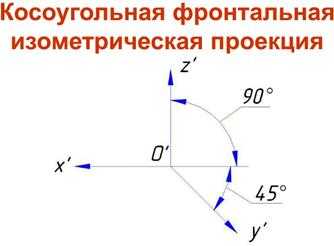
Косоугольная фронтальная изометрия
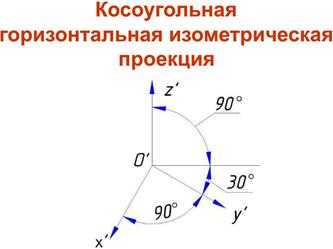
Положение аксонометрических осей приведено на рис. 4, а. Аксонометрические оси Х и Z составляют угол 90°, а ось У образует угол 45° по отношению к горизонтальной линии. Этот угол допускается применять равный 30 или 60°.
Действительные коэффициенты искажения по осям Х, У, Z равны единице: u = v = w = 1. Соответственно линейные размеры предметов изображаются без искажения по всем трем осям.
Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на аксонометрическую плоскость в виде окружности. Окружности, лежащие в плоскостях, параллельных горизонтальной и профильной плоскостям проекций, - в эллипсы (рис. 4, б).
Косоугольная горизонтальная изометрия
Косоугольная горизонтальная изометрическая проекция характерна тем, что все линии предмета, параллельные горизонтальной плоскости проекций, изображаются в горизонтальной изометрии без искажения.
Положение аксонометрических осей приведено на рис. 5, а. Аксонометрические оси Х и У составляют угол 90°, ось У образует угол 30° по отношению к горизонтальной линии. Этот угол допускается применять равный 45 или 60°.
Действительные коэффициенты искажения по осям Х, У, Z равны единице: u = v = w = 1. Соответственно линейные размеры предметов изображаются без искажения по всем трем осям.
Окружности, лежащие в плоскостях, параллельных горизонтальной плоскости проекций, проецируются на аксонометрическую плоскость в виде окружности. Окружности, лежащие в плоскостях, параллельных фронтальной и профильной плоскостям проекций, - в эллипсы (рис. 5, б).
Косоугольная фронтальная диметрия
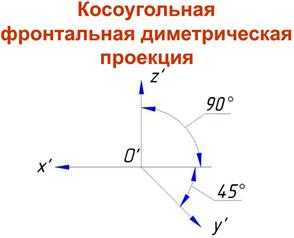
Положение аксонометрических осей в косоугольной фронтальной диметрической проекции приведено на рис. 6, а. Аксонометрические осиХиZсоставляют угол 90°, а осьУобразует угол 45° по отношению к горизонтальной линии. Этот угол допускается применять равный 30 или 60°.
Действительные коэффициенты искажения по осям Х и Z равны единице: u = w = 1;по оси У– вдвое меньше: v = 0,5. Соответственно линейные размеры предметов по оси У сокращаются в два раза.
Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на аксонометрическую плоскость в виде окружности. Окружности, лежащие в плоскостях, параллельных горизонтальной и профильной плоскостям проекций, – в эллипсы (рис. 6, б).
Кривые Безье (https://learn.javascript.ru/bezier)
Кривая Безье задаётся опорными точками.
Их может быть две, три, четыре или больше. Например:
По двум точкам: По трём точкам: По четырём точкам:
Если вы посмотрите внимательно на эти кривые, то «на глазок» заметите:
1. Точки не всегда на кривой. Это совершенно нормально, как именно строится кривая мы рассмотрим чуть позже.
2. Степень кривой равна числу точек минус один. Для двух точек – это линейная кривая (т.е. прямая), для трёх точек – квадратическая кривая (парабола), для четырёх – кубическая.
3. Кривая всегда находится внутри выпуклой оболочки, образованной опорными точками:
Благодаря последнему свойству в компьютерной графике можно оптимизировать проверку пересечений двух кривых. Если их выпуклые оболочки не пересекаются, то и кривые тоже не пересекутся.
Основная ценность кривых Безье для рисования – в том, что, двигая точки, кривую можно менять, причём кривая при этом меняется интуитивно понятным образом.
У кривых Безье есть математическая формула.
Как мы увидим далее, для пользования кривыми Безье знать её нет особенной необходимости, но для полноты картины – вот она.
Координаты кривой описываются в зависимости от параметра t⋲[0,1]
· Для двух точек:
P = (1-t)P1 + tP2
· Для трёх точек:
P = (1−t)2P1 + 2(1−t)tP2 + t2P3
· Для четырёх точек:
P = (1−t)3P1 + 3(1−t)2tP2 +3(1−t)t2P3 + t3P4
Вместо Pi нужно подставить координаты i-й опорной точки (xi, yi).
Эти уравнения векторные, то есть на для каждой из координат:
· x = (1−t)2x1 + 2(1−t)tx2 + t2x3
· y = (1−t)2y1 + 2(1−t)ty2 + t2y3
Вместо x1, y1, x2, y2, x3, y3 подставляются координаты трёх опорных точек, и в то время как t пробегает множество от 0 до 1, соответствующие значения (x, y) как раз и образуют кривую.
Кубический сплайн
Некоторая функция f(x) задана на отрезке , разбитом на части , . Кубическим сплайном дефекта 1 называетсяфункция , которая:
· на каждом отрезке является многочленом степени не выше третьей;
· имеет непрерывные первую и вторую производные на всём отрезке ;
· в точках выполняется равенство , т. е. сплайн интерполирует функцию f в точках .
Для однозначного задания сплайна перечисленных условий недостаточно, для построения сплайна необходимо наложить какие-то дополнительные требования.
Естественным кубическим сплайном называется кубический сплайн, удовлетворяющий также граничным условиям вида:
Теорема: Для любой функции и любого разбиения отрезка существует ровно один естественный сплайн S(x), удовлетворяющий перечисленным выше условиям.
Эта теорема является следствием более общей теоремы Шёнберга-Уитни об условиях существования интерполяционного сплайна.
На каждом отрезке функция есть полином третьей степени , коэффициенты которого надо определить. Запишем для удобства в виде:
тогда
Условия непрерывности всех производных до второго порядка включительно записываются в виде
stydopedia.ru
9. АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ ПРЕДМЕТОВ
Рис. 59. Пример нанесения размеров симметрично расположенных элементов
На технических чертежах изделие изображается в виде ортогональных проекций (видов, разрезов, сечений). Недостатком ортогональных проекций является то, что они не дают непосредственного представления о форме изображенного предмета. Так, каждый основной вид представляет собой точное отображение только одной грани. Чтобы представить по этим видам полную форму предмета, необходимо иметь соответствующие навыки.
Для наглядного объемного представления о предмете применяют аксонометрические проекции по ГОСТ 2.317 – 69 [9], которые позволяют одним изображением передать общую форму предмета.
Аксонометрическая проекция – это проекция предмета на одну плоскость, относительно которой ни одна грань предмета в форме параллелепипеда не расположена параллельно или перпендикулярно. При таком проецировании видны три грани предмета (искаженные), и изображение получается наглядным. В общем случае для предметов любой формы, в том числе и круглых, для построения аксонометрического изображения предмет проецируют на некоторую плоскость вместе с осями прямоугольных координатX,Y иZ, к которым предмет отнесен в пространстве. Направление взгляда при этом не должно совпадать с направлениями координатных осей.
Аксонометрическое изображение дает общее наглядное представление о форме предмета, но не передает точно действительную форму и размеры поверхностей.
Если направление проецирования перпендикулярно к плоскости проекций, то на этой плоскости получают п р я м о у г о л ь н у ю аксонометрическую проекцию (рис. 60, а), если не перпендикулярно – т о к о с о у г о л ь н у ю (рис. 60, б).
Для использования в учебной практике рекомендуются два вида аксонометрических проекций – прямоугольная изометрическая и косоугольная фронтальная диметрическая.
Рис. 60. Построение проекций:
а – ортогональной, б – аксонометрической
30
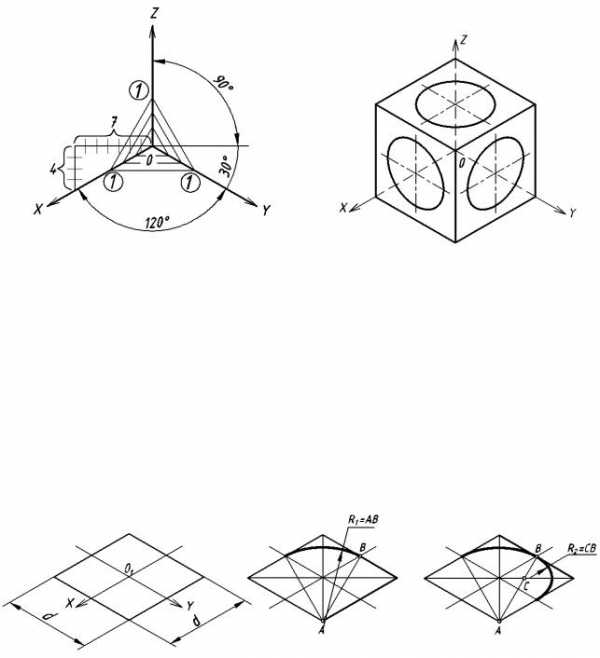
9.1. Прямоугольная изометрическая проекция
Прямоугольной изометрической проекцией (прямоугольной изометрией) называется ак-
сонометрическая проекция, у которой углы между аксонометрическими осями равны 120°, а коэффициенты искажения по всем трем осям равны единице (рис. 61).
Прямоугольные грани, проецируются в виде параллелограммов, а окружности, лежащие на этих гранях проецируются в виде эллипсов. На рис. 62 показано изображение куба и окружностей на его гранях в прямоугольной изометрии. Построение эллипсов заменяется в учебном курсе более простым построением овалов, которое приведено на рис. 63. Эллипсы в каждой грани строятся одинаково.
Рис. 61. Расположение аксонометрических осей | Рис. 62. Изображение куба и окружностей |
в прямоугольной изометрии | на его гранях в прямоугольной изометрии |
П о с т р о е н и е э л л и п с о в . Построим эллипс на верхней грани куба.
Этап 1 (рис. 63, а). Наметим на грани центр эллипса – точку01. Проведем через нее изометрические осиX иY (они параллельны сторонам верхней грани). Отложим в обе стороны от точки01 на каждой оси отрезки, равные радиусу окружности. Через полученные точки проведем прямые, параллельные осям. Получим ромб, представляющий изометрическую проекцию квадрата, в который вписана окружность.
Этап 2 (рис. 63, б). Из вершины ромба в точкеА проведем отрезокAB и, взяв его в качестве радиусаR1, построим верхнюю дугу. Аналогично построим нижнюю дугу (на рисунке она не показана).
Этап 3 (рис. 63, в). На пересечении отрезкаАВ с горизонтальной осью ромба определим точкуС, из которой проведем правую дугу радиусомR2, равным отрезкуСВ. Так же построим левую дугу, которая на рисунке не показана.
Рис. 63. Построение эллипсов в прямоугольной изометрии
31
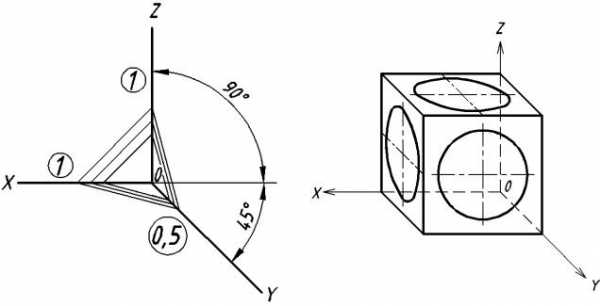
9.2. Косоугольная фронтальная диметрическая проекция
Косоугольной фронтальной диметрической проекцией (фронтальной диметрией) назы-
вается аксонометрическая проекция, у которой углы между аксонометрическими осями располагаются так, как показано на рис. 64. Коэффициенты искажения по осям X иZ равны единице, а по осиY–0,5.
Особенностью этого вида аксонометрии является то, что грань, параллельная координатной плоскости X0Z, и находящаяся на ней окружность проецируются без искажений (рис. 65). Две другие видимые грани и окружности на них проецируются с искажениями: грани в виде равновеликих параллелограммов, а окружности в виде равновеликих эллипсов, причем большие оси этих эллипсов равны1,06d, а малые –0,35d (d – диаметр исходной окружности). Построение упрощенных эллипсов как овалов показано на рис. 66.
Рис. 64. Расположение аксонометрических осей | Рис. 65. Изображение куба и окружностей |
в косоугольной фронтальной диметрии | на его гранях |
П о с т р о е н и е э л л и п с о в . Построим эллипс, например, на верхней грани куба в плоскости X0Y (см. рис. 66).
Этап 1. Наметим в плоскостиX0Y центр эллипса – точку01. Проведем через нее горизонтальную и вертикальную оси; под углом7°14´ к этим осям построим прямые, задающие направления осей эллипса. На этих прямых отложим большую (отрезокА1В1) и малую (отрезокC1D1) оси эллипса с центром в точке01.
Этап 2. Отложим в обе стороны от точки01 на продолжениях осиC1D1 отрезки, равные диаметру исходной окружностиd и определим точки04 и05 (05 на рис. 66 не показана). Из точек04 и05 проведем дуги радиусомR = 04D1.
Этап 3. На пересечении отрезка04E1 с большой осью эллипсаА1В1 определим точку06, из которой радиусомR1 = 06A1 = 06E1 проведем левую дугу. Аналогично построим правую дугу.
Подобным образом на грани Z0Y построим эллипс с центром в точке03. Разница будет только в наклоне большойА3В3 и малой осейC3D3.
В плоскости X0Z построим окружность без искажения ее формы и размера с центром в точ-
ке 02.
32
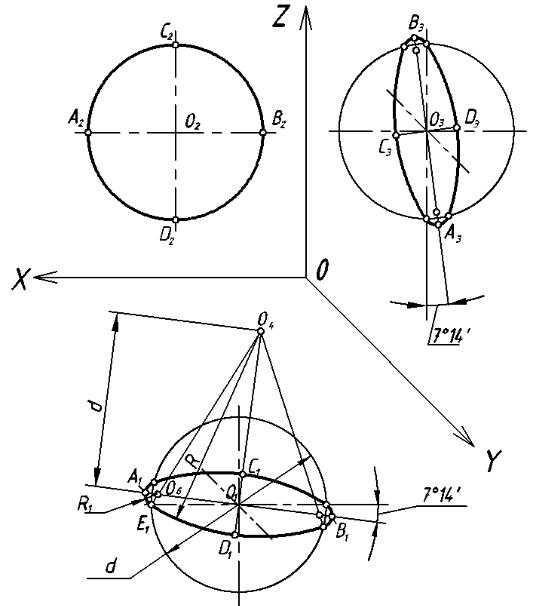
Рис. 66. Построение эллипсов во фронтальной диметрии
9.3.Разрезы в аксонометрических проекциях
Ваксонометрических проекциях предметов для показа внутренней конфигурации, как правило, выполняют разрезы двумя и более взаимно перпендикулярными секущими плоскостями, параллельными координатным плоскостям X0Z,Y0Z илиX0Y. Эти разрезы образуют вырез, на котором видно внутреннее строение предмета. Если предмет имеет две плоскости симметрии (вид сверху симметричен относительно двух осей), то обычно выполняют так называемый «четвертной вырез», при котором секущие плоскости совпадают с плоскостями симметрии (рис. 67). В предметах с одной плоскостью симметрии или несимметричных секущие плоскости должны проходить по осям отверстий и центрам полостей любой формы (рис. 68). Разрезы на ортогональных изображениях чертежа могут не совпадать с разрезами в аксонометрических проекциях. Линии штриховки сечений наносят параллельно одной из диагоналей проекций квадратов, построенных в соответствующих координатных плоскостях (см. рис. 61, 64). Штриховка пересекающихся сечений должна быть встречной. Ниже приведены примеры аксонометрических изображений предметов с «вырезами» (рис. 67, 68).
33
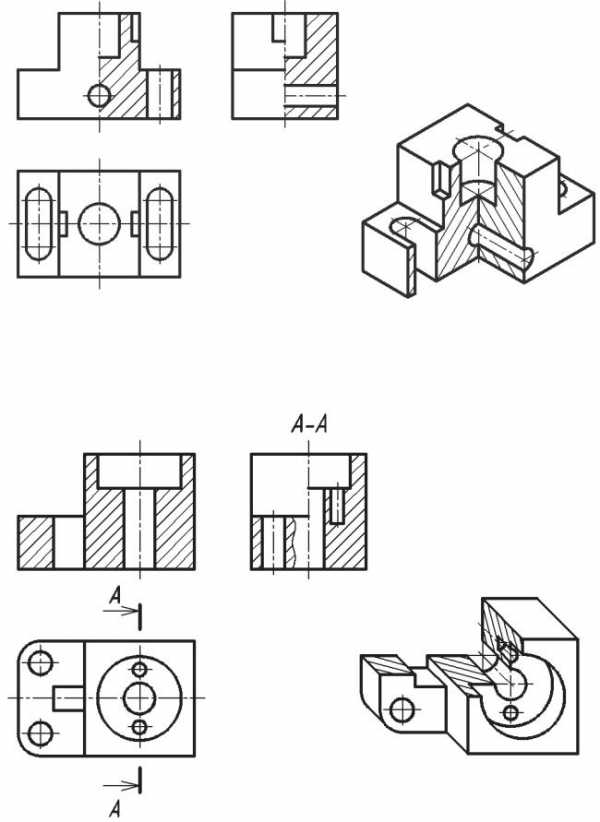
Рис. 67. Прямоугольная изометрическая проекция с «четвертным вырезом»
Рис. 68. Косоугольная фронтальная диметрическая проекция с «вырезом»
34
studfiles.net
Фронтальная косоугольная диметрия - Энциклопедия по машиностроению XXL
На рис. 441 дано изображение крышки сальника во фронтальной косоугольной диметрии. [c.314]| Рис.58. Оси фронтальной косоугольной диметрии |  |
Из частных видов аксонометрических проекций, предусмотренных государственным стандартом, чаше всего используют ортогональную изометрию, ортогональную диметрию, фронтальную (косоугольную) диметрию. [c.34]
Вид аксонометрических проекций назначен вверху чертежей заданий в виде сокращенных наименований ПИ — прямоугольная изометрия, ПД — прямоугольная диметрия, ФД — фронтальная (косоугольная) диметрия. [c.53]
На рис. 78, б пирамида изображена во фронтальной косоугольной диметрии. Условно принято, что ось х проходит через вершину пирамиды А, а ось у — через вершину С. Аксонометрическая проекция вершины пирамиды В найдена с помощью координат х и у (значение координаты у взято уменьшенным в 2 раза). Из точки параллельно оси г откладывают высоту пирамиды (3 3 = ЗгР ) " соединяют полученную вершину 5 с вершинами треугольника основания. Видимые ребра обводят сплошными линиями, а невидимые — штриховыми. [c.72]Так как в косоугольной диметрии передняя Изображение окружности. Способ графиче-фронтальная грань детали изображается так ского определения направления главных осей же, как главный вид ортогонального чертежа, для верхнего эллипса показан на фиг. 417. то косоугольную диметрию часто называют фронтальной проекцией. [c.173]
На рис. 74, а изображено проецирование окружностей во фронталь ной косоугольной диметрии. Окружности, расположенные в плоскости, параллельной фронтальной плоскости проекций, проецируются на [c.66]
Каковы показатели искажения для косоугольной фронтальной диметрии [c.85]
Из косоугольных аксонометрических проекций ГОСТом предусмотрено применение фронтальных изометрии и диметрии. [c.146]
На рис. 1 17 показано пооперационное построение косоугольной фронтальной диметрии по ее ортогональным проекциям (рис. 118). На рис. 119 показана косоугольная фронтальная диметрия и комплексный чертеж из ортогональных проекций корпуса (рис. 120). [c.88]
ГОСТ 2.317—69 (СТ СЭВ 1979—79) устанавливает прямоугольные и косоугольные аксонометрические проекции. Прямоугольные проекции делятся на изометрические и диметрические, косоугольные — на фронтальные изометрические, горизонтальные изометрические и фронтальные диметр ические. [c.72]
Косоугольная фронтальная диметрия. На практике часто бывает полезным построение такой аксонометрической проекции, в которой хотя бы одна из координатных плоскостей не искажалась. Очевидно, что для выполнения этого условия плоскость проекций должна быть параллельной одной из координатных плоскостей. При этом нельзя пользоваться ортогональным проецированием, так как координатная ось, [c.230]
На практике направление оси у выбирают таким, чтобы углы, образованные осью у с осями X иг, равнялись бы 135°, а показатель искажения V = 0,5 (рис. 235). Такую косоугольную аксонометрию называют фронтальной диметрией. [c.231]
Предварительно напомним, что ортогональная проекция шара является кругом того же диаметра, а его косоугольная проекция является эллипсом ( 47). Поэтому в приведенных стандартных ортогональных изометрии и диметрии очерк шара будет окружностью соответственно диаметров 1,22й и 1,06 , а во фронтальной диметрии очерк шара будет эллипсом. [c.238]
На рис. 4.2в показана косоугольная (фронтальная) диметрия с такими же коэффициентами искажения, как и у прямоугольной (1 - по осям X и Z и 0,5 - по оси Y ). Ее оси Х и Z расположены взаимно перпендикулярно, а ось Y под углом 45° к оси X. Отрезки, расположенные на осях X и Z, не искажаются при проецировании, а отрезки, расположенные на оси У", проецируются с уменьшением вдвое. Эту аксонометрию применяют для изображения предметов с окружностями во фронтальных плоскостях, так как они на аксонометрическую проекцию проецируются без искажения (рис. 4.3). [c.87]
Из косоугольных аксонометрических проекций ГОСТ предусмотрено применение фронтальной диметрии. [c.215]Поэтому косоугольную фронтальную диметрию и косоугольные изометрии целесообразно применять в тех случаях, когда деталь имеет несколько окружностей, расположенных в одной или параллельных плоскостях. [c.67]
На рис. 77, б призма изображена в косоугольной фронтальной диметрии, причем условно принято, что аксонометрическая ось г совпадает с ребром призмы СО. [c.70]
В соответствии с ГОСТ 2.317—69 изометрическую проекцию рекомендуется строить без сокращения по осям X, у и Z, а диметрическую — без сокращения по осям X и 2 и с сокращением в два раза по оси у. Тем самым в изометрии все размеры, измеряемые вдоль аксонометрических осей, увеличиваются в 1/0,82 = 1,22, а в диметрии в 1/0,94 = 1,06 раза. В косоугольной (фронтальной) диметрической проекции показатели искажения по осям х и 2 равны 1, а по оси у — 0,5. [c.85]
Изображение окружностей в косоугольной (фронтальной) диметрии приведено на рис. 122. [c.92]
Как изображаются окружности в косоугольной (фронтальной) диметрии [c.92]
Постройте прямоугольную изометрию и косоугольную (фронтальную) диметрию куба, грани которого параллельны плоскостям проекций. В видимые грани куба впишите окружности. [c.92]
Так как эти фигуры расположены параллельно фронтальной плоскости проекций, то в косоугольной (фронтальной) изометрии и диметрии, у которых плоскость аксонометрических проекций параллельна фронтальной [c.50]
В тех случаях, когда необходимо выявить какую-либо важную характерную часть объекта, сохранив неизменной ее форму, целесообразно остановиться на косоугольной аксонометрии — изометрии или диметрии. Аксонометрическое изображение на рис. 286 выполнено во фронтальной ко со угол ной изометрии. Все части объекта, расположенные параллельно фронтальной картинной плоскости (в данном случае — несущая конструкция покрытия), спроецировались без искажений. [c.225]
В косоугольной аксонометрии также направления специально не показываются и не обозначаются. Нетрудно заметить, что в этом случае, если у оригинала нет окружностей в координатных плоскостях XOY и ZOY, то отличить косоугольную фронтальную изометрию от косоугольной фронтальной диметрии можно только по размерам, нанесенным на чертеже. [c.134]
Принятое правило нанесения линий штриховки помогает отличить косоугольные фронтальные изометрию и диметрию. [c.136]
| Рис. 3.57. Аксонометрические оси косоугольной фронтальной диметрии | 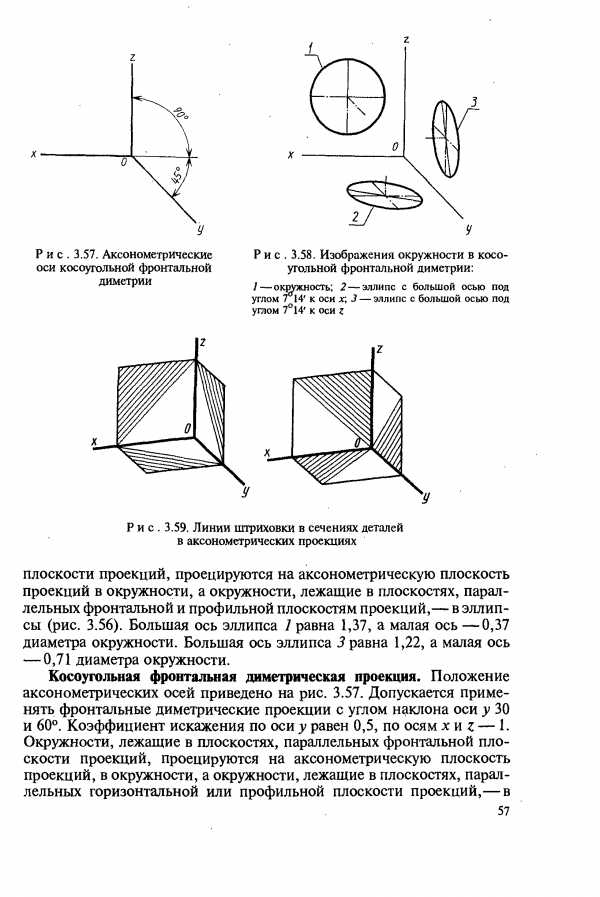 |
Куб, грани которого параллельны координатным плоскостям, изображен в косоугольной изометрии на рис. 473, о, в косоугольной диметрии на рис. 473, б. Окружность, вписанная во фронтально расположенную грань, изображается в виде окружности это объясняется тем, что плоскость этой грани куба параллельна плоскости X П г, а следовательно, и плоскости П ° (см. /43/). Аксонометрии окружностей, расположенных в других видимых гранях куба, представляют собой эллипсы, вписанные в ромбы (изометрия) и в параллелограммы (диметрия). Оси эллипсов всегда наклонены к горизонтальному направлению на чертеже. Когда аксонометрическая ось у (или х) наклонена к горизбн-тальному направлению под углом 45 , то больщая ось эллипсов а иЬ в косоугольной изометрии равна 1,30, малая — 0,541). При том же наклоне оси у (или х) в косоугольной диметрии большая ось эллипсов равна 1,070, а малая ось — 0,33 В. [c.186]
Выражение изобразить наглядно, дать наглядное изображение, означает построить изображение н косоугольной фронтальной диметри-ческой проекции (хотя бы в известной под названием кабинетная ). [c.6]
В косоугольной фронтальной диметрии для линий штриховки в сечениях фронтал ьными илек, костями сохраняется угол 45 к горизонтали.. [c.34]
Рис, 4. Пример оформления изображения в прнмоу олышй изометрии и косоугольной фронтальной диметрии втулки с резьбой, которую и.зобра-жают в аксонометрии услов)Ю по ГОСТ 2.311—68. Допускается изображать в сечениях профиль резьбы полностью или частично. [c.34]
Наиболее часто применяют косоугольную фронтальную диметрию, D которой плоскость хОг параллельна плоскости П, поэтому аксоно-петрические оси О х и О г взаимно перпендикулярны и показатели искажения по ним равны единице и = w = 1. Направление оси О у и показатель искажения v могут быть выбраны произвольно. [c.153]
На практике часто бывает полезным построение такой аксонометрической проекции, в которой хотя бы одна из координатных плоскостей не искажалась. Очевидно, что для выполнения этого условия плоскость проекций должна быть параллельной одной из координатных плоскостей. При этом нельзя пользоваться ортогональным проецированием, так как координатная ось, перпендикулярная указанной координатной плоскости, изобразится точкой, и изображение будет лгапено наглядности. Поэтому пользуются косоугольным проецированием. Направление оси у выбирают таким, чтобы углы, образованные осью У с осями х" и z, равнялись бы 135°, а показатели искажения были бы равны по осям х и z, т.е. р=г=1, по оси у q=0,5. Такую косоугольную аксонометрию называют фронтальной диметрией. [c.36]
Нанесение на разрезах штриховки в косоугольной диметрической проекции выполняется, как и в прямоугольной диметрии (фиг. 199). Откладывают по осям О х и O z отрезки произвольной, но одинаковой величины, а по оси О у — половину этого отрезка. Линии, соединяющие концы этих отрезков, определянэт направление штриховки в плоскости O x z — для фронтального с чения, в плоскости О х у — для горизонтального, в плоскости О у г — для профильного. [c.124]
Косоугольная аксонометрическая проекция — фронтальная диметрия — значительно больше искажает предмет, особенно если он ограничен поверхностями вращения. Фронтальная диметрия применяется при изображении сравнительно несложных предметов, имеющих большое число окружностей, расположенных во взаимно параллельных плоскостях. Если изображаемый предмет расположить так, чтобы эти плоскости оказались парал-ьными картинной (аксонометрической) плоскости вкций, то окружности будут проецироваться на нее [c.17]
mash-xxl.info
Прямоугольная диметрическая проекция
В прямоугольной диметрической проекции аксонометрические оси Ooxo иOozo составляют между собой угол 97о10’. ОсьOoyo является биссектрисой оставшегося угла, составляя с двумя другими осями равные углы 131о25’ (рис. 11). При построении этой проекции принимают, что
Kx=KzиKy= 0,5Kx.
Тогда по основной теореме аксонометрии получаем из формулы
K2x+ K2y + K2z = 2, что 2K2x+ (0,5Kx)2 = 2,
тогда K2x= 8/9;Kx= 0,94.
Приведенные коэффициенты искажения будут равны:
Kx= Kz = 1; Ky = 0,5,
что соответствует увеличению изображения в 1,06 раза (1/0,94 = 1,06).
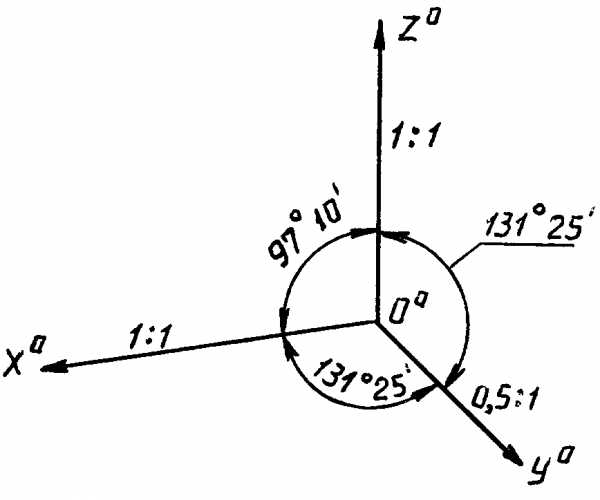
Рис. 11
Прямоугольная диметрия рекомендуется к применению в случае, когда наибольшее число характерных особенностей сосредоточено на одной стороне предмета. Наиболее отличающаяся особенностями сторона предмета располагается параллельно плоскости XoOoZo.Косоугольная фронтальная диметрическая проекция
Аксонометрическая плоскость располагается параллельно фронтальной плоскости проекций V (рис. 12). Поэтому аксонометрические оси Ooxo иOozo параллельны декартовым осямOxиOz. Соответственно, коэффициенты искаженияKx=Kz. ЗначениеKyпринимается равным 0,5. Расположение аксонометрических осей показано на рисунке .
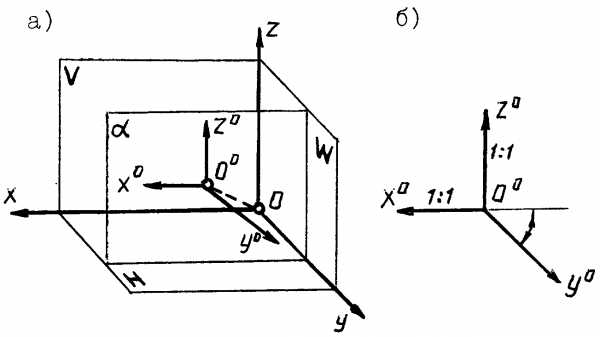
Рис. 12
Косоугольная фронтальная диметрия удобна в тех случаях, когда изображаемая геометрическая фигура содержит большое число окружностей (или других кривых, состоящих из дуг окружностей), лежащих на взаимно параллельных плоскостях. При расположении этих плоскостей параллельно аксонометрической плоскости, все окружности будут проецироваться на ней также в виде окружностей, что упрощает построение.Комплексный чертеж точки и прямой
План:
3.1. Комплексный чертеж точки
3.2. Проекции прямых общего положения
3.3. Проекции прямых уровня
Горизонталь - прямая равных высот
Фронталь - прямая равных глубин
Профильная прямая - прямая равных широт
3.4. Проекции проецирующих прямых
Горизонтально-проецирующая прямая
Фронтально-проецирующая прямая
Профильно-проецирующая прямая
3.5. Определение натуральной величины отрезка прямой общего положения
3.6. Деление отрезка прямой в данном отношени
Комплексный чертеж точки
Внутри трехгранного угла, образованного горизонтальной (H), фронтальной (V) и профильной (W) плоскостями проекций, расположим какую-либо точку А (рис. 13).
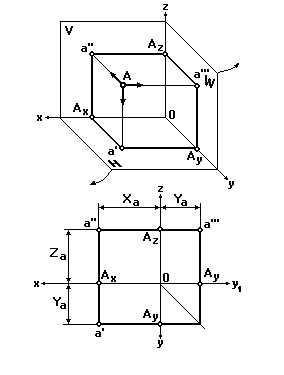
Рис. 13
Направим проецирующий луч перпендикулярно плоскости V. Точка пересечения этого луча с плоскостью V будет фронтальной проекцией a'' точкиA. Спроецируем точку А на плоскость H и получим ее горизонтальную проекциюa'. Проецируя точку А на плоскость W, получим ее профильную проекциюa'''.Для получения чертежа необходимо все три плоскости V, H и W вместе с построенными на них проекциями совместить в одну плоскость, т.е. развернуть их.
При этом плоскость H поворачивается вокруг оси xна 90 градусов книзу, плоскость W — вокруг осиzна 90 градусов вправо, а плоскость V остается неподвижной (при этом осьyкак бы раздваивается).
В результате совмещения получают чертеж точки в трех проекциях. Очертания плоскостей H, V и W на чертеже не показывают.
Линию, связывающую горизонтальную и профильную проекции точки А, представляют двумя отрезками ломаной линии. Вершина ее лежит на биссектрисе угла, образованного осями yиy1. Эту биссектрису называютпостоянной линией чертежа.
Прямые линии, соединяющие проекции точки и перпендикулярные осям проекций, называют линиями проекционной связи(рис. ).
Координатный отрезок, равный превышению точки А над плоскостью H, называют высотойZa(аппликатой) точки А. Координатный отрезок, равный расстоянию от точки А до плоскости V, называютглубинойYa(ординатой) точки А. Координатный отрезок, равный расстоянию от точки А до плоскости W, называютширотойXa(абсциссой) точки А.
Горизонтальная проекция точки А определяется на эпюре ее координатами XaиYa, а фронтальная — координатамиXaиZa(рис. 13).
studfiles.net
Проекция фронтальная диметрическая косоугольная - Энциклопедия по машиностроению XXL
Какова особенность фронтальной диметрической косоугольной проекции [c.313]Если проецирующие лучи направлены под углом к аксонометрической плоскости проекций, то получается косоугольная аксонометрическая проекция. К косоугольным аксонометрическим проекциям относятся фронтальная изометрическая, горизонтальная изометрическая и фронтальная диметрическая проекции. [c.77]
Косоугольная фронтальная диметрическая проекция Z l [c.78]
КОСОУГОЛЬНАЯ ФРОНТАЛЬНАЯ ДИМЕТРИЧЕСКАЯ ПРОЕКЦИЯ [c.84]ГОСТ 2.317—69 (СТ СЭВ 1979—79) устанавливает прямоугольные и косоугольные аксонометрические проекции. Прямоугольные проекции делятся на изометрические и диметрические, косоугольные — на фронтальные изометрические, горизонтальные изометрические и фронтальные диметр ические. [c.72]
Косоугольная фронтальная диметрическая проекция является упрощением прямоугольной диметрической проекции, в которой ось расположена по горизонтали перпендикулярно оси 2, а ось у — под углом 45° к оси X. [c.308]
В косоугольной фронтальной диметрической проекции по обе стороны от точки О на оси у откладывают то же количество равных частей, вдвое уменьшенных по величине. Из точек деления радиусами, равными половине величины соответствующей хорды, описывают окружности, соединив которые по касательной к окружностям плавной кривой получи,м очертание фигуры в виде эллипса. [c.321]
Косоугольная фронтальная диметрическая проекция. Аксонометрическая ось Z направлена вертикально, ось X - горизонтально, ось Y - под углом 45° к горизонтали (черт. 201, а). Допускается наклон оси Y под углом 30° и 60°. [c.84]
Пример косоугольной фронтальной диметрической проекции приведен на черт. 199, б. [c.84]
КОСОУГОЛЬНАЯ ДИМЕТРИЧЕСКАЯ ПРОЕКЦИЯ (ФРОНТАЛЬНАЯ) [c.123]
Задача 131. Задать на чертеже натуральные оси координат и выполнить три технических рисунка (в прямоугольных изометрической и диметрической, а также фронтальной диметрической проекциях) шара с приданием рисункам рельефности, используя для этой цели сечения шара плоскостями параллельными горизонтальной плоскости проекций для прямоугольных проекций и фронтальной плоскости проекций для косоугольной аксонометрической проекции. [c.49]
В косоугольной фронтальной диметрической проекции (рис. 28, в) по обе стороны от точки О на оси у откладывают то же количество равных частей, вдвое уменьшенных по величине. Из точек деления [c.318]
Фронтальную диметрическую проекцию рекомендуется применять в тех случаях, когда целесообразно сохранить неискаженными фигуры, расположенные в плоскостях, параллельных фронтальной плоскости проекции. В том же случае, когда преследуют цель сохранить без искажения фигуры, расположенные в горизонтальных плоскостях, картину (плоскость К) располагают параллельно плоскости Н и принимают все показатели искажения равными единице. Этот вид косоугольной изометрической проекции обычно называется военной перспективой (рис. 453). [c.319]
Из всего многообразия аксонометрических проекций ГОСТ 2.317— 69 Единой системы конструкторской документации устанавливает для выполнения чертежей и схем пять видов — два вида прямоугольных аксонометрических проекций (изометрическую и диметрическую) и три вида косоугольных (фронтальную изометрическую, фронтальную диметрическую и горизонтальную изометрическую). [c.104]
Косоугольная фронтальная диметрическая проекция удобна в тех случаях, когда предмет имеет большое количество окружностей, или сложных по форме плоских фигур, лежащих в параллельных плоскостях. Располагая эти плоскости параллельно плоскости аксонометрических проекций, мы получаем возможность вычерчивать сложные плоские фигуры без искажений. [c.113]
ГОСТ 2.317—69 устанавливает следующие разновидности аксонометрических проекций прямоугольные (изометрическая и ди-метрическая) косоугольные (фронтальная изометрическая, горизонтальная изометрическая, фронтальная диметрическая). [c.152]
Фронтальная диметрическая проекция является косоугольной, так как направление проецирования 8Т составляет острый угол с плоскостью аксонометрических проекций Р. Фронтальной она называется потому, что передняя грань располагается фронтально и изображается без искажения, как в натуре. [c.73]
В зависимости от наклона осей координат, к которым отнесен изображаемый предмет, к аксонометрической плоскости и угла, составляемого проецирующими лучами с этой, плоскостью, образуются различные аксонометрические проекции. Если проецирующие лучи перпендикулярны картинной плоскости, то проекция называется прямоугольной. Если проецирующие лучи наклонны к ней, то проекция называется косоугольной. Мы рассмотрим наиболее употребляемые в технике следующие виды аксонометрических проекций, рекомендуемые ГОСТ 2.317—69 (СТ СЭВ 1979—79) из косоугольных — фронтальную диметрическую (рис. 76, а), из прямоугольных — изометрическую (рис. 76, 6) и диметрическую (рис. 76, а). [c.43]
В соответствии с ГОСТ 2.317—69 изометрическую проекцию рекомендуется строить без сокращения по осям X, у и Z, а диметрическую — без сокращения по осям X и 2 и с сокращением в два раза по оси у. Тем самым в изометрии все размеры, измеряемые вдоль аксонометрических осей, увеличиваются в 1/0,82 = 1,22, а в диметрии в 1/0,94 = 1,06 раза. В косоугольной (фронтальной) диметрической проекции показатели искажения по осям х и 2 равны 1, а по оси у — 0,5. [c.85]
Из большого множества возможных вариантов аксонометрических проекций наибольшее распространение на практике получили прямоугольная изометрическая проекция, прямоугольная диметрическая проекция и фронтальная (косоугольная) диметрическая проекция . [c.13]
Более полное представление о вентиляционных системах дают схемы воздуховодов. Для таких аксонометрических схем чаще всего применяют косоугольную диметрическую проекцию (фронтальную). [c.185]
Косоугольная фронтальная диметрическая проекция (коэффициенты искажения по осям Ку = 0,5 = к — ) — рис. 80, [c.62]
Фронтальная диметрическая проекция относится к косоугольным аксонометрическим проекциям, так как ее получают с помощью проецирующих прямых, не перпендикулярных плоскости аксонометрических проекций Р. Для построения фронтальной ди- [c.119]
Для построения наглядных изображений предметов ГОСТ 3453—59 рекомендует применять следующие виды аксонометрических проекций прямоугольные — изометрическую и диметрическую проекции косоугольную — фронтальную диметрическую проекцию (выбирая в каждом отдельном случае наиболее подходящую из них). [c.112]
Косоугольная фронтальная диметрическая проекция. Положение аксонометрических осей приведено на рис. 3.57. Допускается применять фронтальные диметрические проекции с углом наклона оси у 30 и 60°. Коэффициент искажения по оси у равен 0,5, по осям хи г — 1. Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на аксонометрическую плоскость проекций, в окружности, а окружности, лежащие в плоскостях, параллельных горизонтальной или профильной плоскости проекций,— в [c.57]
Если проецирующие лучи направлены к плоскости проекций под любым острым углом, то проецирование называется косоугольным. Из косоугольных проекций вы знаете фронтальную диметрическую, как одну из аксонометрических проекций. [c.111]
Фронтальная косоугольная диметрическая проекция пирамиды показана на рис. 151,6. [c.85]
Штриховка при разрезах во фронтальной косоугольной диметрической проекции показана на рис. 212,а и б. Направление штриховки находят, откладывая по осям о х и o z любые отрезки одинаковой длины, а по оси оу-половину отрезка а (0,5а). Аналогично выполняют штриховку в прямоугольной диметрической проекции. [c.116]
Наиболее просто построение контура детали криволинейного очертания во фронтальной косоугольной диметрической проекции, так как в этой проекции деталь изображается без искажений. [c.120]
Переплет имеет два форзаца. Один форзац (передний, с аксонометрическими сетками / и 2) служит для построения от руки наглядных чертежей (эскизов) н технических рисунков в косоугольной фронтальной диметрической проекции (сетка /) и в прямоугоизометрической проекции (сетка 2). По этим образцам легко построить аналогичные сетки и для других видов аксонометрических проекций, установленных по ГОСТ 2.317—69. [c.365]
Косоугольная фронтальная диметрическая проеющя. Из косоугольных аксонометрических проекций рассмотрим фронтальную диметрическую проекцию, широко используемую в учебном процессе. Положение аксонометрических осей для нее [c.151]
На рис. 457 показана стандартная фронтальная диметрическая проекция Ф сферы Ф. Эллипс А В С О, являющийся очерковой линией Ф, огибает семейство круговых сечений сферы, параллельных плоскости П, которые проектируются на нее без искажения. Точки и найдены при помощи вспомогательной плоскости П", перпендикулярной к плоскости П и параллельной оси Ох они являются фокусами очеркового эллипса Л Д С П. Этот же эллипс является косоугольной проекцией на плоскости П круга АВСО, плоскость которого перпендикулярна к направлению проектирования s, а его малая ось СО — проекцией диаметра СО круга АВСО, а также проекцией круга СОЕР, параллельного направлению проектирования. [c.381]
Косоугольная фронтальная диметрическая проекция является упрощением диметрической проекции, в которой ось х расположена по горизонтали перпендику-ггярно оси г, а под углом 45° к оси л — ось у. [c.307]
Для аксонометрических изображений предметов применяют пять видов аксонометрических проекций (ГОСТ 2.317—69 ) прямоугольные — изометрические и ди-метрические, косоугольные — фронтальные диметрические, фронтальные изомет- [c.57]
ЕСКД ГОСТ 2.317-69 (СТ СЭВ 1979—79) установлены следующие типы аксонометрии прямоугольная (изометрическая и диметрическая проекции) косоугольная (фронтальная изометрическая, горизонтальная изометрическая и фронтальная диметрическая проекции). Допускается применение других теоретически обоснованных аксонометрических проекций. [c.97]
Итак, в стандарте дана косоугольная диметрическая проекция, причем благодаря выбору направления плоскости аксонометрических проекций окружности, расположенные параллельно фронтальной плоскости проекций, остаются окружностями и в аксонометрической проекции. СЗтсюда рассматриваемая проекция применима не только при вычерчивании тел с прямолинейными очертаниями, но и с круглыми. Однако, если окружности расположены в горизонтальных и профильных плоскостях, изображения их получаются искаженными. Чертить в кабинетной проекции цилиндрические и конические тела следует лишь в том случае, когда их оси вращения перпендикулярны фронтальной плоскости проекций. [c.46]
mash-xxl.info