Как построить развертку пирамиды. Пирамида развертка
Правильные пирамиды - Mnogogranniki.ru - создание моделей многогранников из бумаги
Готовый набор "Волшебные грани"
Для сборки многогранников мы можем вам предложить уже готовые развёртки - вырезанные и подогнутые.
Для этого вам нужно воспользоваться деталями набора Волшебные грани № 14.
Кроме того, в самом выпуске вы найдете информацию о строении многогранников.
Сборка правильной четырехугольной пирамиды:
Вращение готового многогранника, собранного из этих деталей:
Сборка усечённой четырехугольной пирамиды:
Вращение готового многогранника, собранного из этих деталей:
Сборка пирамиды со звёздчатым основанием:
Вращение готового многогранника, собранного из этих деталей:
Сборка би-пирамиды с основанием в форме пятиконечной звезды:
Вращение готового многогранника, собранного из этих деталей:
mnogogranniki.ru
Правильная пирамида развертка | МеханикИнфо
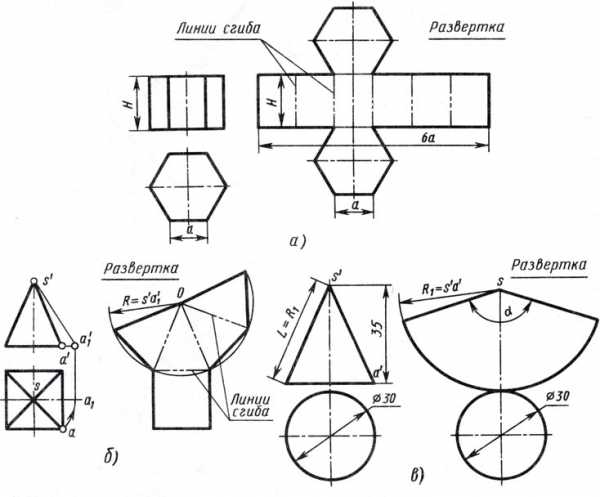
Правильная пирамида. имеющая в основании правильный n — угольник (в данном случае шестиугольник), показана на рис. 1. Для удобства построения одно из ребер, например O’V’ расположено в плоскости, параллельной фронтальной проекции.
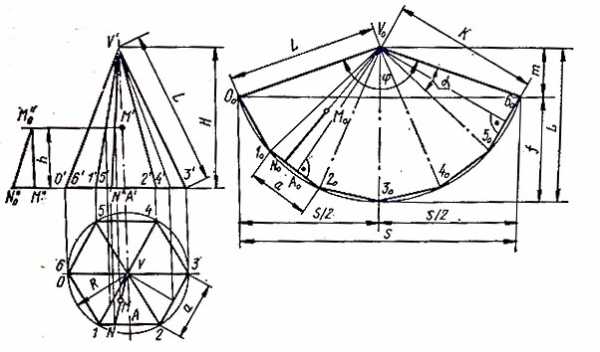
Рис. 1. Правильная пирамида развертка.
Поэтому на рисунке показана его натуральная величина. Построение развертки боковой поверхности следует начинать с произвольной точки V0, из нее как из центра радиусом, равным длине бокового ребра пирамиды R = L, описывается дуга. От произвольной точки O0 на дуге n раз последовательно откладывается сторона многоугольника. Полученные точки 00, 10, …, 60 последовательно соединяются между собой и с высотой V0.
Если дана точка М, принадлежащая одной из плоскостей пирамиды, то ее можно перенести на развертку следующим образом. Проводится прямая MV до пересечения со стороной основания в точке N и соответственно М’V’ до пересечения в точке N’. Расстояние 1N откладывается от точки 10 на стороне 1020 развертки до точки N0. Проводится прямая N0V0. Для определения действительной длины отрезка NM нужно построить вспомогательный прямоугольный треугольник со сторонами N”0M” = NM и М”М”0 = h. От точки N0 откладывается расстояние N”0M”0. Получаем точку М0.
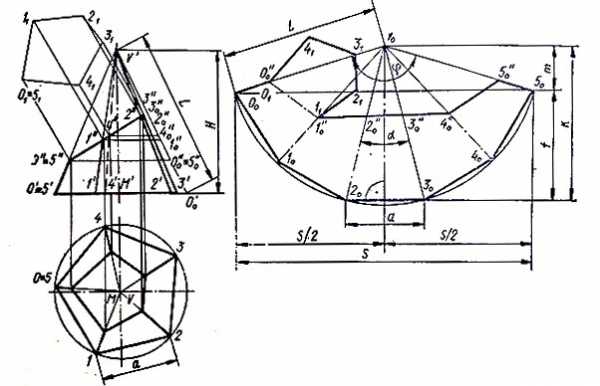
Рис. 2. Правильный пятиугольник усеченный плоскостью.
Для аналитического определения элементов разверток пирамиды используют ряд зависимостей; боковое ребро ,
высота треугольников, составляющих развертку боковой поверхности ; тангенс половины плоского угла при вершине пирамиды:
полный угол развертки ᵠ = nα.
Величины s, m и f можно определить, воспользовавшись зависимостями:
;
.
Для четного количества плоскостей пирамиды (рис. 1):
.
Для нечетного количества плоскостей пирамиды (рис. 2):
.
mechanicinfo.ru
Усечённые правильные пирамиды - Mnogogranniki.ru
Готовый набор "Волшебные грани"
Для сборки многогранников мы можем вам предложить уже готовые развёртки - вырезанные и подогнутые.
Для этого вам нужно воспользоваться деталями набора Волшебные грани № 14.
Кроме того, в самом выпуске вы найдете информацию о строении многогранников.
Сборка правильной четырехугольной пирамиды:
Вращение готового многогранника, собранного из этих деталей:
Сборка правильной четырехугольной пирамиды:
Вращение готового многогранника (усечённой четырехугольной пирамиды), собранного из этих деталей:
Сборка пирамиды со звёздчатым основанием:
Вращение готового многогранника, собранного из этих деталей:
Сборка би-пирамиды с основанием в форме пятиконечной звезды:
Вращение готового многогранника, собранного из этих деталей:
mnogogranniki.ru
Как построить развертку пирамиды
Развертка пирамиды – это фигура, которая образуется при последовательном совмещении плоских элементов поверхности с плоскостью чертежа. Пирамида относится к многогранной поверхности, ее плоскими элементами являются грани в виде треугольников. При выполнении развертки любой поверхности обязательно соблюдение основных правил: размеры всех элементов должны иметь натуральную величину; площадь построенной развертки равняется площади развертываемой поверхности.
Вам понадобится
- Карандаш, линейка, циркуль, треугольник.
Инструкция
Пример. Построить полную развертку трехгранной пирамидыОснование пирамиды – треугольник АВС – параллельно горизонтальной плоскости проекций П₁. Значит горизонтальная проекция А₁В₁С₁ равна натуральной величине.
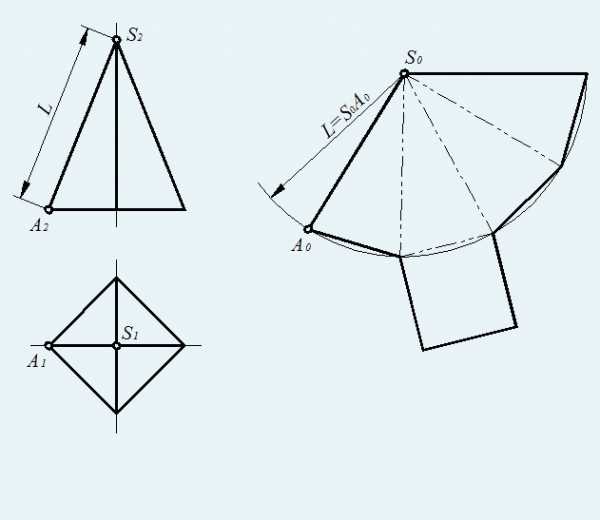
- Боковая поверхность пирамиды состоит из граней, имеющих форму треугольника. Способом прямоугольного треугольника определите натуральную величину ребер SC и SB. Для этого на плоскости П₂ начертите высоту фронтальной проекции пирамиды h и обозначьте точку S₀.
- Под прямым углом к высоте h от ее основания отложите горизонтальные проекции S₁С₁ и S₁В₁. Точки В₀ и С₀ соедините с точкой S₀ – получите S₀В₀ и S₀С₀ – натуральную величину ребер SB и SC.
- Ребро AS(A₂S₂, A₁S₁) является фронтальной прямой, значит, A₂S₂ – ее натуральная величина.
- Имея истинные размеры всех граней пирамиды, постройте ее развертку. Отложите отрезок А₀С₀=А₁С₁ на произвольной горизонтальной прямой. Из точки А₀ сделайте засечку радиусом A₂S₂ (н.в. АS), а из точки С₀ – засечку радиусом S₀С₀ (н.в. SC), получите точку S ₀.
- Треугольник А₀S₀C₀ – одна из граней пирамиды. Достройте смежные ее грани. Из точки С₀ сделайте засечку радиусом С₁В₁, а из точки S₀ радиусом S₀В₀ (н.в. SB) – получите точку В₀.
- Из точки В₀ сделайте засечку радиусом В₁А₁, а из точки S₀ – радиусом A₂S₂. Отметьте точку А₀.
- К прямой А₀C₀ засечками достройте основание пирамиды – треугольник АВС. Это будет полная развертка данной трехгранной пирамиды.
completerepair.ru
РАЗВЁРТКА ТРЕУГОЛЬНОЙ ПИРАМИДЫ - Пирамида (геометрия) — Википедия
6 5. Площадью полной поверхности пирамиды называется… Развертка боковой поверхности пирамиды представляет собой плоскую фигуру, состоящую из треугольников – граней пирамиды и многоугольника – основания. Конус называется вписанным в пирамиду, если вершины их совпадают, а его основание вписано в основание пирамиды.
С развертками поверхностей мы часто встречаемся в обыденной жизни, на производстве и в строительстве. Для одних тел развертки могут быть точными, для других — приближенными. Точные развертки имеют все многогранники (призмы, пирамиды и др.), цилиндрические и конические поверхности и некоторые другие. Приближенные развертки имеют шар, тор и другие поверхности вращения с криволинейной образующей. При построении разверток многогранников придется находить действительную величину ребер и граней этих многогранников с помощью вращения или перемены плоскостей проекций.
Точки на развертке принято обозначать теми же буквами, как и на комплексном чертеже, но с индексом 0 (нулевое). При построении развертки прямой призмы по комплексному чертежу (рис. 171, а) высоту граней берут с фронтальной проекции, а ширину — с горизонтальной. Длина развертки при таком построении получается несколько меньше действительной длины развертки.
К развертке боковой поверхности пристраивают основания цилиндра. Значительно труднее построение развертки пирамиды (рис. 174, а). Ее ребра SA и SC являются прямыми общего положения и проецируются на обе плоскости проекций искажением.
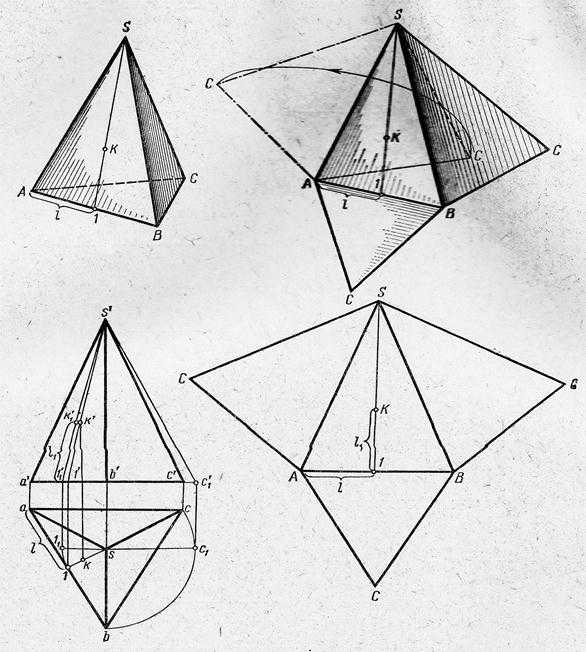
Длины сторон этого треугольника можно взять непосредственно с развертки, как показано на чертеже. Делят окружность основания на равные части, например на 12 частей (рис. 175, а), и представляют, что в конус вписана правильная двенадцатиугольная пирамида. Согласитесь, вы намного быстрее догадаетесь, о чем идет речь, если услышите слово “пирамида”. Пирамида – это в первую очередь геометрическая фигура, а потом все остальное.
Геометрические фигуры. Пирамида
По числу углов основания бывают следующие пирамиды треугольные, четырёхугольные и т. д. Пирамида это частный случай конуса. Пирамида, как и другие многогранники, были известны с древних времен и имеет богатую историю. Слово пирамида имеет много значений. Еще в Древней Греции словом «пирамис» называли пшеничный пирог, напоминавший форму египетских пирамид. Затем это слово стало означать сложный термин «монументальную структуру имеющая квадратную площадь в основании с наклонными сторонами, встречающимися на вершине».
Первым, кто установил, чему был равен объем пирамиды является Демокрит, а доказал все это Евдокс Книдский. Евклид называет пирамиду телесной фигурой, которая ограничивается плоскостями, от одной плоскости, т. е. основания и сходятся в одной точке, т. е. вершине.
Развертка и схема пирамиды. Как сделать пирамиду из бумаги самому
С началом развития наук в XVIII веке, пирамида становиться не просто древнейшим памятников архитектуры, а также правильной геометрической фигурой имеющей четыре симметричные стороны. В современном Египте “пирамида” – является собирательным образом, у каждой из пирамид есть свое имя: пирамида Хеопса, пирамида Хефрена и т.д. Египтяне называли пирамиду “Mr”, правильно произносится, как “мэр”. Но происхождение слова “мэр” осталось загадкой.
Не менее грандиозны пирамиды индейцев майя в Мексике. Сейчас можно встретить большое количество сувениров в форме пирамиды, они завораживают и кажется содержат в себе нечто таинственное. В противном случае пирамида называется неправильной (фиг.286,в). В правильной пирамиде все боковые ребра равны между собой (как наклонные с равными проекциями).
Высота точки S равна высоте пирамиды. Натуральные размеры сторон основания выявлены на его горизонтальной проекции. III, б. Изображаем ребра S’A, S’C’ и S’B’ пирамиды, соединяя вершину S’ с вершинами основания А’В’С’.
Из истории пирамид
Начало геометрии пирамиды было положено в Древнем Египте и Вавилоне, однако активное развитие получило в Древней Греции. Объем пирамиды был известен древним египтянам. Развёрткой называется плоская фигура, полученная при совмещении поверхности геометрического тела с одной плоскостью (без наложения граней или иных элементов поверхности друг на друга). Приступая к изучению развёртки поверхности, последнюю целесообразно рассматривать как гибкую, нерастяжимую плёнку.
При этом, если отсек поверхности может быть совмещён с плоскостью без разрывов и склеивания, то такую поверхность называют развёртывающейся, а полученную плоскую фигуру — её развёрткой. Причём описать цилиндр около пирамиды можно только тогда, когда в основании пирамиды — вписанный многоугольник (необходимое и достаточное условие). Тетраэдром называется треугольная пирамида.
Правильная треугольная пирамида — это пирамида с правильным треугольником в основании (грани же должны быть равнобедренными треугольниками). Площадь треугольной пирамиды рассчитывается, как сумма площадей основания и боковой развертки. Также ее можно найти, если рассчитать площадь одной из боковых граней и основания. Пусть дана треугольная пирамида. В целом, найти объем правильной треугольной пирамиды очень просто.
Для построения развертки необходимо предварительно определить истинные длины боковых ребер пирамиды. Прямоугольник, квадрат, треугольник, трапеция и другие – геометрические фигуры из раздела точной науки. Пирамида – это многогранник. Основанием этой фигуры является многоугольник, а боковыми гранями треугольники, имеющие общую вершину, или трапеции. Используют самый разнообразный материал, из которого выполняется пирамида.
Слово пирамида на разных языках мира
Создать макет поможет метод преобразования плоских предметов в объемные многогранники и определенные знания из геометрии. Прежде всего определим, какой будет пирамида. Развертка данной фигуры является основой для изготовления объемной фигуры. Допустим, необходимо изготовить макет правильной треугольной пирамиды. Данная фигура имеет основанием правильный многоугольник, а ее вершина спроецирована в его центр. В качестве основания выбран равносторонний треугольник.
Пирамидой называется многогранник, у которого одна из граней – основание – какой – нибудь многоугольник, а все остальные – боковые – треугольники, имеющие общую вершину.
Уже опубликовано на сайте:
labrowendosin.ru
Наклонная пирамида развертка. | МеханикИнфо
Наклонная пирамида развертка. Усеченная четырехгранная пирамида. 4.14/5 (82.86%) проголосовало 7
Наклонная усеченная пирамида с четырехугольным основанием показана на рис. 1.
Через точки 0′, 0′1 и 2′, 2′1 проводятся прямые до пересечения в точке V’, являющейся вершиной пирамиды.
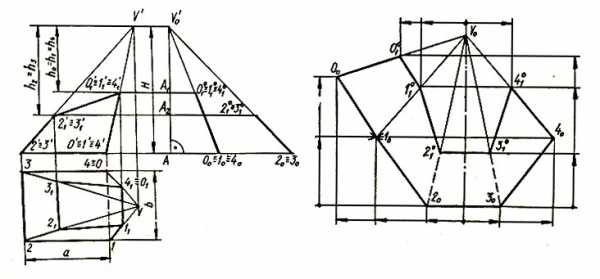
Рис. 1.
Для определения действительном длины ребер пирамиды через произвольную точку А проводят две перпендикулярные прямые. На горизонтальной линии от точки А откладываются расстояния V0, V1,…,V4 до точек 00, 10, 20,…,40. На вертикальной линии откладывается высота пирамиды Н до точки V’0. Расстояния 00V’0, 10V’0,…, 40V’0 представляют собой действительные длины ребер. Для построения развертки необходимо из произвольной точки V0 отложить отрезок V000 = V’000. Из центров V0 и 00 радиусами соответственно V010 = V’010 и 0010 = 01 описываются дуги до пересечения в точке 10. Из центров V0 и 00 описываются дуги радиусами V020 = V’020 и 1020 = 12 до пересечения в точке 20. Построение продолжается по описанному способу до получения точки 40. Точки 10, 20, 30 и 40 последовательно соединяются между собой и каждая с V0.
Развертка усеченной пирамиды четырехугольной.
Действительная длина ребер малого основания определяется следующим образом. От точки V’0 откладываются расстояния h0 = h2 = h5 до точки А1 и h3 = h4 до точки А2. Через точки А1 и А2 проводятся горизонтальные прямые до пересечения V’000 и V’020 в точках 001 = 101 = 401 и 201 = 301. Из центра V0 радиусом V’0001 описывается дуга до пересечения V000, V010 и V040 соответственно в точках 001, 101 и 401. Радиусом V’0201 из центра V0 описывается дуга до пересечения V020 и V030 в точках 201 и 301, Полученные точки 001, 101, 401 последовательно соединяются, расстояния 001101, 101201 являются действительными длинами ребер малого основания.
mechanicinfo.ru
Пирамида - развертка. Развертка пирамиды для склеивания. Развертки из бумаги
Прямоугольник, квадрат, треугольник, трапеция и другие – геометрические фигуры из раздела точной науки. Пирамида - это многогранник. Основанием этой фигуры является многоугольник, а боковыми гранями треугольники, имеющие общую вершину, или трапеции. Для полного представления и изучения любого геометрического объекта изготавливают макеты. Используют самый разнообразный материал, из которого выполняется пирамида. Поверхность многогранной фигуры, развернутая на плоскости, называется ее разверткой. Создать макет поможет метод преобразования плоских предметов в объемные многогранники и определенные знания из геометрии. Развертки из бумаги или картона изготовить непросто. Потребуется умение выполнять чертежи по заданным размерам.
Материалы и приспособления
Моделирование и выполнение многогранных объемных геометрических фигур - интересный и захватывающий процесс. Из бумаги можно выполнить большое количество всевозможных макетов. Для работы будут необходимы:
- бумага или картон;
- ножницы;
- карандаш;
- линейка;
- циркуль;
- ластик;
- клей.
Определение параметров
Прежде всего определим, какой будет пирамида. Развертка данной фигуры является основой для изготовления объемной фигуры. Выполнение работы потребует предельной точности. При неправильном чертеже геометрическую фигуру собрать будет невозможно. Допустим, необходимо изготовить макет правильной треугольной пирамиды.
Любое геометрическое тело обладает определенными свойствами. Данная фигура имеет основанием правильный многоугольник, а ее вершина спроецирована в его центр. В качестве основания выбран равносторонний треугольник. Данное условие определяет название. Боковые ребра у пирамиды – это треугольники, количество которых зависит от выбранного для основания многогранника. В данном случае их будет три. Также важно знать размеры всех составных частей, из которых будет составлена пирамида. Развертки из бумаги выполняются в соответствии с учетом всех данных геометрической фигуры. Параметры будущей модели оговариваются заранее. От этих данных зависит выбор используемого материала.
Как выполняется развертка правильной пирамиды?
Основой модели является лист бумаги или картона. Работу начинают с чертежа пирамиды. Фигура представляется в развернутом виде. Плоское изображение на бумаге соответствует заранее выбранным размерам и параметрам. Правильная пирамида имеет основанием правильный многоугольник, а высота проходит через его центр. Изготавливаем для начала простую модель. В данном случае – это треугольная пирамида. Определяем размеры выбранной фигуры.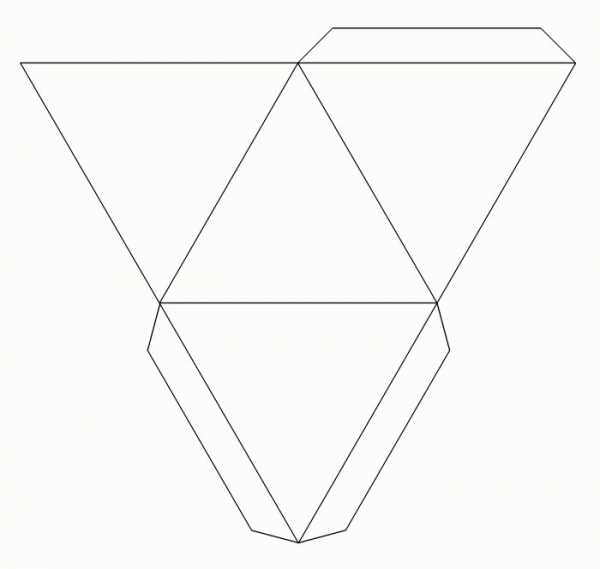 
Чтобы построить развертку пирамиды, основанием которой является правильный треугольник, в центре листа, используя линейку и карандаш, нарисуем основание заданных размеров. Далее к каждой его стороне вычерчиваем боковые грани пирамиды – треугольники. Теперь переходим к их построению. Размеры сторон треугольников боковой поверхности измеряем циркулем. Ножку циркуля ставим в вершину нарисованного основания и делаем засечку. Действие повторяем, перемещаясь в следующую точку треугольника. Пересечение, полученное в результате таких действий, определит вершины боковых граней пирамиды. Их соединяем с основанием. Получаем чертеж пирамиды. Для склеивания объемной фигуры на сторонах боковых граней предусматривают клапаны. Дорисовываем небольшие трапеции.
Сборка макета
Вырезаем ножницами выполненный рисунок по контуру. Аккуратно сгибаем развертку по всем линиям. Клапаны-трапеции заправляем внутрь фигуры таким образом, чтобы ее грани сомкнулись. Их смазываем клеем. Через тридцать минут клей высохнет. Объемная фигура готова.
Развертка четырехугольной пирамиды
Сначала представим, как выглядит геометрическая фигура, макет которой будем изготавливать. Основанием выбранной пирамиды является четырехугольник. Боковые ребра - треугольники. Для работы используем те же материалы и приспособления, что и в предыдущем варианте. Чертеж выполняем на бумаге карандашом. В центре листа чертим четырехугольник с выбранными параметрами.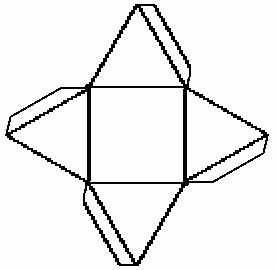
Каждую сторону основания делим пополам. Проводим перпендикуляр, который будет являться высотой треугольной грани. Раствором циркуля, равным длине боковой грани пирамиды, делаем на перпендикулярах засечки, установив его ножку в вершину основания. Оба угла одной стороны основания соединяем с полученной точкой на перпендикуляре. В результате получаем в центре чертежа квадрат, на гранях которого нарисованы треугольники. Чтобы зафиксировать модель на боковых гранях, дорисовывают вспомогательные клапаны. Для надежного крепления достаточно полоски сантиметровой ширины. Пирамида готова к сборке.
Завершающий этап выполнения макета
Полученную выкройку фигуры вырезаем по контуру. По начерченным линиям сгибаем бумагу. Сбор объемной фигуры производят путем склеивания. Предусмотренные клапаны смазываем клеем и фиксируем полученную модель.
Объемные макеты сложных фигур
После выполнения простой модели многогранника можно перейти к более сложным геометрическим фигурам. Развертка пирамиды усеченной намного сложнее в выполнении. Ее основаниями являются подобные многогранники. Боковые грани – это трапеции. Последовательность выполнения работы будет такой же, как та, в которой изготавливалась простая пирамида. Развертка будет более громоздкой. Для выполнения чертежа используют карандаш, циркуль и линейку.
Построение чертежа
Развертка пирамиды усеченной выполняется в несколько этапов. Боковой гранью усеченной пирамиды является трапеция, а основаниями - подобные многогранники. Допустим, что это квадраты. На листе бумаги выполняем чертеж трапеции с заданными размерами. Боковые стороны полученной фигуры продлеваем до пересечения. В результате получаем равнобедренный треугольник. Его сторону измеряем циркулем. На отдельном листе бумаги строим окружность, радиусом которой будет измеренное расстояние.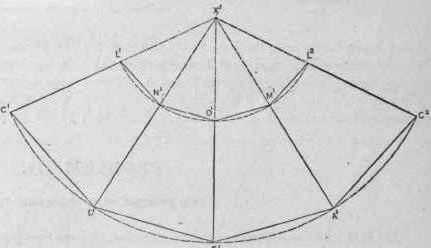
Следующий этап – это построение боковых ребер, которые имеет усеченная пирамида. Развертка выполняется внутри нарисованной окружности. Циркулем измеряют нижнее основание трапеции. На окружности отмечаем пять точек, которые соединяют линии с ее центром. Получаем четыре равнобедренных треугольника. Циркулем измеряем сторону трапеции, нарисованной на отдельном листе. Данное расстояние откладываем на каждой стороне нарисованных треугольников. Полученные точки соединяем. Боковые грани трапеции готовы. Остается только нарисовать верхнее и нижнее основания пирамиды. В данном случае это подобные многогранники – квадраты. К верхнему и нижнему основаниям первой трапеции дорисовываем квадраты. На чертеже изображены все части, которые имеет пирамида. Развертка практически готова. Остается только дорисовать соединительные клапаны на сторонах меньшего квадрата и одной из граней трапеций.
Завершение моделирования
Перед склеиванием объемной фигуры чертеж по контуру вырезают ножницами. Далее развертку аккуратно сгибают по начерченным линиям. Крепежные клапаны заправляем внутрь модели. Их смазываем клеем и прижимаем к граням пирамиды. Модели даем высохнуть.
Изготовление разных моделей многогранников
Выполнение объемных моделей геометрических фигур - увлекательное занятие. Чтобы его досконально освоить, следует начинать с выполнения самых простых разверток. Постепенно переходя от простых поделок к более сложным моделям, можно приступать к созданию самых замысловатых конструкций.
4u-pro.ru
