Косоугольная проекция. Проекция косоугольная

Косоугольная проекция - это... Что такое Косоугольная проекция?

Косоугольная проекция

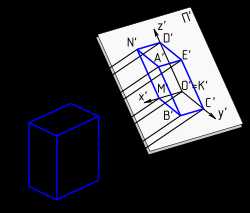
Проецирование параллелепипеда на плоскость П'.

Аксонометрическая проекция (греч. άχοπ — «ось» и «метрия») — способ изображения геометрических предметов на чертеже при помощи параллельных проекций.

Предмет с системой координат, к которой он отнесён, проецируют на произвольную плоскость (картинная плоскость аксонометрической проекции) таким образом, чтобы эта плоскость не совпадала с его координатной плоскостью. В этом случае получается две взаимосвязанные проекции одной фигуры на одну плоскость, что позволяет восстановить положение в пространстве, получив наглядное изображение предмета. Так как картинная плоскость не параллельна ни одной из координатных осей, то имеются искажения отрезков по длине параллельных координатным осям. Это искажение может быть равным по всем трём осям — изометрическая проекция, одинаковыми по двум осям — диметрическая проекция и с искажениями разными по всем трём осям — триметрическая проекция.

Стандартизированные аксонометрические проекции [1]

прямоугольная проекция (направление проецирования перпендикулярно к плоскости проекции):
косоугольная проекция (направление проецирования не перпендикулярно к плоскости проекции):
- фронтальная изометрическая проекция;
- фронтальная диметрическая проекция;
- горизонтальная изометрическая проекция.

См. также

Проекция (геометрия)

Источники

↑ По ГОСТ 2.317-69 — Единая система конструкторской докуметации. Аксонометрические проекции.

Литература

Богданов В. Н., Малежик И. Ф., Верхола А. П. и др. Справочное руководство по черчению.. — М.: Машиностроение., 1989. — С. 864. — ISBN 5-217-00403-7
Под ред. Ишлинский А. Ю. Новый политехнический словарь.. — М.: Большая Российская энциклопедия., 2003. — С. 671. — ISBN 5-7107-7316-6
Фролов С. А. Начертательная геометрия.. — 2-е изд., перераб. и доп.. — М.: Машиностроение., 1983. — С. 240.

Wikimedia Foundation. 2010.

Косоугольная система координат

Коспас

Смотреть что такое "Косоугольная проекция" в других словарях:

косоугольная проекция — pražulnioji projekcija statusas T sritis fizika atitikmenys: angl. oblique projection vok. schiefwinklige Projektion, f rus. косая проекция, f; косоугольная проекция, f pranc. projection oblique, f … Fizikos terminų žodynas
косоугольная проекция — 3.3 косоугольная проекция: Аксонометрическая проекция, у которой направление проецирования неперпендикулярно к плоскости проецирования. Источник: ГОСТ 2.317 2011: Единая система конструкторской документации. Аксонометрические проекции … Словарь-справочник терминов нормативно-технической документации
Проекция косоугольная — Косоугольная проекция: аксонометрическая проекция, у которой направление проецирования неперпендикулярно к плоскости проецирования... Источник: ГОСТ 2.317 2011. Межгосударственный стандарт. Единая система конструкторской документации.… … Официальная терминология
Проекция (геометрия) — У этого термина существуют и другие значения, см. Проекция. Проекции Параллельная Прямоугольная (ортогональная) Аксонометрическая Изометрическая Диметрическая Триметрическая Косоугольная Аксонометрическая Изометрическая Диметрическая… … Википедия
Аксонометрическая проекция — Проекции Параллельная Прямоугольная (ортогональная) Аксонометрическая Изометрическая Диметрическая Триметрическая Косоугольная Аксонометрическая Изометрическая Диметрическая Триметрическая Перспективная (центральная) … Википедия
косая проекция — pražulnioji projekcija statusas T sritis fizika atitikmenys: angl. oblique projection vok. schiefwinklige Projektion, f rus. косая проекция, f; косоугольная проекция, f pranc. projection oblique, f … Fizikos terminų žodynas
Изометрическая проекция — Проекции Параллельная Прямоугольная (ортогональная) Аксонометрическая Изометрическая Диметрическая Триметрическая Косоугольная Аксонометрическая Изометрическая Диметрическая Триметрическая Перспективная (центральная) … Википедия
Ортогональная проекция — Проекции Параллельная Прямоугольная (ортогональная) Аксонометрическая Изометрическая Диметрическая Триметрическая Косоугольная Аксонометрическая Изометрическая Диметрическая Триметрическая Перспективная (центральная) Прочие Птичий глаз Рыбий глаз … Википедия
Параллельная проекция — Проекции Параллельная Прямоугольная (ортогональная) Аксонометрическая Изометрическая Диметрическая Триметрическая Косоугольная Аксонометрическая Изометрическая Диметрическая Триметрическая Перспективная (центральная) Прочие Птичий глаз Рыбий глаз … Википедия
Центральная проекция — Проекции Параллельная Прямоугольная (ортогональная) Аксонометрическая Изометрическая Диметрическая Триметрическая Косоугольная Аксонометрическая Изометрическая Диметрическая Триметрическая Перспективная (центральная) Прочие Птичий глаз Рыбий глаз … Википедия

dic.academic.ru

5. Косоугольное проецирование

При параллельном проецировании проецирующие лучи параллельны между собой.

Косоугольное проецирование- это частный случай параллельного проецирования. При нем проецирующие лучи наклонены к плоскости проекций, угол не равен 90○.

Косоугольное проецирование используется для построения теней и построения аксонометрических проекций

Как он вчера говорил: Есть одна плоскость без искажения (фронтальная или горизонтальная).

Примером искажения является тень предметов в утреннее или вечернее время.

Косоугольное проецирование применяется в основном при решении позиционных задач, что значительно упрощает построения, связанные с решением задач на пересечение прямых с плоскостями и взаимное пересечение плоскостей, когда необходимо получить вырожденные проекции названных геометрических образов, т.е. прямую превратить в точку, а плоскость – в прямую. Косоугольное проецирование может быть как центральным, так и параллельным.

Свойства:

Проекцией точки является точка.
Проекцией линии является линия.
Проекцией прямой в общем случае является прямая. (Если прямая совпадает с проецирующим лучом, то её проекцией является точка).
Если точка принадлежит линии, то проекция точки принадлежит проекции линии.
Точка пересечения линий проецируется в точку пересечения проекций этих линий.
В общем случае плоский многогранник проецируется в многогранник с тем же числом вершин.
Проекции параллельных прямых параллельны.
Если точка делит длину отрезка в отношении m:n, то проекция этой точки делит длину проекции отрезка в том же отношении.
Плоская фигура, параллельная плоскости проекций, проецируется без искажения.

Пример:

П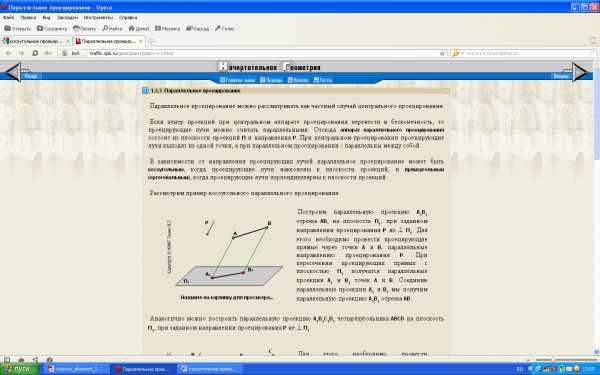остроим параллельную проекцию А1В1 отрезка АВ, на плоскость П1, при заданном направлении проецирования Р не П1. Для этого необходимо провести проецирующие прямые через точки А и В, параллельные направлению проецирования Р. При пересечении проецирующих прямых с плоскостью П1 получатся параллельные проекции А1 и В1 точек А и В. Соединив параллельные проекции А1 и В1 мы получим параллельную проекцию А1В1 отрезка АВ.

6. Центральное проецирование

Наиболее общий случай получения проекций пространственных фигур - это центральное проецирование.

Вэтом случае проецирующиелучи выходят из одной точки - центра проецирования S, который находится на конечном расстоянии от плоскости проекций П1.

Для того чтобы получить центральные проекции точек А и B, необходимо провести проецирующие лучи из центра проецирования S через точки А и B до пересечения с плоскостью проекций П1. При пересечении получаются точки А1 и B1 - центральные проекции точек А и B.

Для того чтобыопределить положение точки А в пространстве по её центральным проекциям, необходимо иметь две центральные проекции этой точки А1 и А2, полученные из двух различных центров S1 и S2. Если провести проецирующие лучи S1А1 и S2А2, то точка их пересечения однозначно определит положение точки А в пространстве.

Для построения центральной проекции A1B1 отрезка АВ достаточно построить центральные проекции А1 и B1 точек А и В, так как две точки однозначно определяют прямую.

Центральное проецирование обладает большой наглядностью, так как оно соответствует зрительному восприятию предметов.

Свойства центрального проецирования:

Проекцией точки является точка.
Проекцией линии является линия.
Проекцией прямой в общем случае является прямая. (Если прямая совпадает с проецирующим лучом, то её проекцией является точка).
Если точка принадлежит линии, то проекция точки принадлежит проекции линии.
Точка пересечения линий проецируется в точку пересечения проекций этих линий.
В общем случае плоский многогранник проецируется в многогранник с тем же числом вершин.
Проекцией взаимно параллельных прямых является пучок прямых.
Если плоская фигура параллельна плоскости проекций, то её проекция подобна этой фигуре.

7. Прямые и плоскости общего и частного положения Прямая частного положения (или прямая уровня) - прямая, параллельная хотя бы одной из называетсягоризонталью. На горизонтальную плоскость проекций горизонталь проецируется в натуральную величину. Прямая, параллельная фронтальной плоскости проекций, называетсяфронталью. На фронтальную плоскость проекций фронталь проецируется в натуральную величину. Прямая, параллельная профильной плоскости проекций, называетсяпрофильной прямой. На профильную плоскость проекций профильная прямая проецируется в натуральную величину. Прямая называется проецирующей, если она перпендикулярна одной из плоскостей проекций. Одна из проекций такой прямой есть точка. Эта проекция называется главной или вырожденной. Все точки проецирующей прямой являются конкурирующими.

1.Горизонтально проецирующая прямая - прямая горизонтальной плоскости проекций. Горизонтальной проекцией такой прямой является точка, а фронтальная и профильная проекции || оси z.

2.Фронтально проецирующая прямая - прямая фронтальной плоскости проекций. Фронтальной проекцией такой прямой является точка, а горизонтальная и профильная проекции || оси y.

3.Профильно проецирующая прямая - прямая профильной плоскости проекций. Профильной проекцией такой прямой является точка, а горизонтальная и фронтальная проекции || оси x.

Прямой общего положения называется прямая, не параллельная ни одной из плоскостей проекций.№ Плоскость общего положения - плоскость не перпендикулярная ни к одной из плоскостей проекций. Плоскость частного положения - плоскость проходящая через проецирующие прямые, т.е. перпендикулярная к одной или одновременно к двум основным плоскостям проекций. Если плоскость перпендикулярна только к одной плоскости проекций, то она называется проецирующей плоскостью.

Существует три вида проецирующих плоскостей:

1.Горизонтально-проецирующая плоскость - перпендикулярна к П1. И поэтому проецируется на нее как прямая.

2. Фронтально-проецирующая плоскость - перпендикулярна к П2. И поэтому проецируется на нее как прямая.

3. Профильно-проецирующая плоскость - перпендикулярна к П3. И поэтому проецируется на нее как прямая.

На обычном ортогональном чертеже, когда плоскость П3 не используется, профильно-проецирующая плоскость выглядит как плоскость общего положения. Если плоскость перпендикулярна к двум плоскостям проекций, то она называется плоскостью уровня. Следовательно, плоскость уровня всегда параллельна одной из плоскостей проекций. Существует три вида плоскостей уровня: 1. Горизонтальная плоскость уровня - || П1. 2. Фронтальная плоскость уровня - || П2. 3. Профильная плоскость уровня - || П3.

studfiles.net

Косоугольные проекции

⇐ ПредыдущаяСтр 2 из 3Следующая ⇒

Косоугольное проецирование отличается от ортогонального тем, что в нем для объемного видения объекта пучок параллельных проецирующих лучей не ортогонален КП. При этом сам объект и его ОСК остаются неподвижными. Соответственно, Sкос=S. Косоугольное проецирование – основной инструмент для построения тени объекта на плоскости и отражения объекта в плоском зеркале.

Во многих задачах (построение теней и зеркальных отражений, расчет освещенности поверхностей) требуется знать вектор направления на источник проецирующих лучей, выраженный в объектных координатах. В МСК это вектор S. Например, при фронтальном ортогональном проецировании S=[0 0 1], при горизонтальном – S=[0 1 0], профильном – S=[1 0 0], для стандартной диметрии Sдим=[1 1 Ö7], для стандартной изометрии Sизо=[1 1 1].

При косоугольном проецировании вектор направления на проецирующий пучок S=[sx sy sz] составляет с нормалью к ФКП угол проецирования lf такой, что (рис.1):

Косоугольное проецирование на фронтальную плоскость:

p'=pKf

, cx= sx / sz, cy= sy / sz.

Получим коэффициенты осевых искажений, проецируя косоугольно орты ОСК на ФКП:

Þ mx = my = 1,

Углы ориентации проекций осей ОСК на ФКП (рис.2) определяются условиями:

gxy=90°, tg(gyz) = cx / cy = sx / sy, tg(gzx) = tg(90 - gyz + 180) = cy / cx = sy / sx .

Окружности, в плоскостях, параллельных КП, проецируются в окружности, т.е. без искажений. Это главное отличие и основное преимущество косоугольного проецирования перед аксонометрическим, позволяющее избежать построения эллипсов с произвольной ориентацией полуосей.

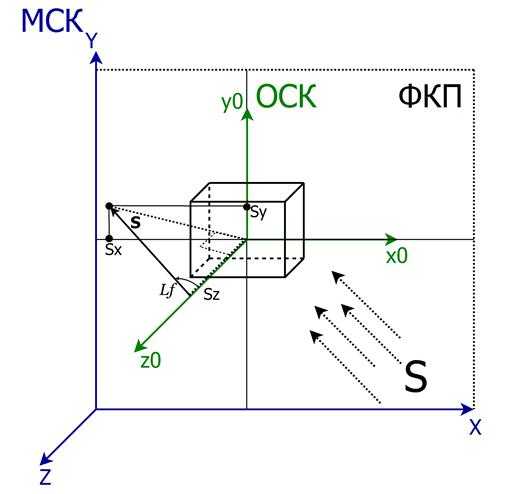
Рис.1. Расчет параметров косоугольной проекции, проекция осей ОСК на ФКП

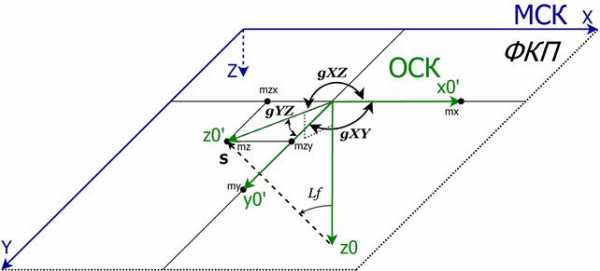
Рис.2. Расчет параметров косоугольной проекции, углы между проекциями осей ОСК на ФКП (g ® g)

Приведем по аналогии без вывода формулы расчета параметров косоугольной горизонтальной и профильной проекций:

Горизонтальная проекция:

, cx = sx / sy, cz = sz / sy.

Получим коэффициенты осевых искажений, проецируя косоугольно орты ОСК на ГКП:

mx = mz = 1,

Углы ориентации проекций осей ОСК на ГКП определяются условиями:

gxz=90°, tg(gyz) = cx / cz = sx / sz, tg(gxy) = cz / cx = sz / sx.

Профильная проекция:

, cy = sy / sx, cz = sz / sx.

Получим коэффициенты осевых искажений, проецируя косоугольно орты ОСК на ПКП:

my = mz = 1,

Углы ориентации проекций осей ОСК на ПКП определяются условиями:

gyz=90°, tg(gzx) = cy / cz = sy / sz, tg(gxy) = cz / cy = sz / sy.

Некоторые направления вектора S дают стандартные косоугольные проекции:

– Кабинетная проекция (косоугольная фронтальная диметрия) образуется при S=[1 1 2Ö2].

Тогда mx = my = 1, mz = 0.5, gxy = 90°, gyz = gzx = 135°.

Данная проекция наиболее наглядна и проста в построении. Часто кабинетной проекцией ошибочно называют построенную на бумаге в клетку косоугольную проекцию с соотношением масштабов 2:2:Ö2, близким к соотношению 2:2:1 кабинетной проекции.

– Кавальерная или военная проекция (косоугольная фронтальная изометрия) образуется при выборе S=[1 1 Ö2].

Тогда mx = my = mz = 1, gxy = 90°, gyz = gzx = 135°.

По сравнению с кабинетной проекцией лучи при кавальерном проецировании проходят более полого, под большим углом к КП. Из-за этого проекции объектов выглядят вытянутыми и несколько неестественными. В то же время кавальерная проекция удобна для измерения длин отрезков, параллельных осям координат. Геометрическая точность и способность отображать объем объясняют использование в старину кавальерных проекций в фортификационном деле.

– Зенитная проекция (косоугольная горизонтальная изометрия) образуется при выборе направления проецирования S=[1 2 Ö3].

Тогда mx = my = mz = 1, gxy = 90°, gyz = 150°, gzx = 120°.

Данная проекция представляет наклонный вид на объект сверху. В аэрофотосъемке используется зенитная диметрия – вид с высоты птичьего полета – с углом наблюдения lh»0° и соотношениями осевых масштабов и координат точки наблюдения mx:my:mz = 1:ky:1, где выбор коэффициента сжатия высоты ky позволяет изображать на чертеже вытянутые вверх объекты – горы, небоскребы, башни.

Если перед косоугольным проецированием выполнить вращения объекта, то получим косоугольную триметрию – наиболее общий вид параллельного проецирования, в котором осевые масштабы связаны условием:

mx2 + my2 + mz2 = 2 + tg2(l)

arhivinfo.ru

Косоугольная проекция Википедия

Проецирование параллелепипеда на плоскость П'.

Аксонометри́ческая прое́кция (от др.-греч. ἄξων «ось» + μετρέω «измеряю») — способ изображения геометрических предметов на чертеже при помощи параллельных проекций.

Предмет с системой координат, к которой он отнесён, проецируют на произвольную плоскость (картинная плоскость аксонометрической проекции) таким образом, чтобы эта плоскость не совпадала с его координатной плоскостью. В этом случае получаются две взаимосвязанные проекции одной фигуры на одну плоскость, что позволяет восстановить положение в пространстве, получив наглядное изображение предмета. Так как картинная плоскость не параллельна ни одной из координатных осей, то имеются искажения отрезков по длине параллельных координатным осям. Это искажение может быть равным по всем трём осям — изометрическая проекция, одинаковыми по двум осям — диметрическая проекция и с искажениями разными по всем трём осям — триметрическая проекция.

Стандартизированные аксонометрические проекции [1]

Аксонометрическая проекция

прямоугольная проекция (направление проецирования перпендикулярно к плоскости проекции):
косоугольная проекция (направление проецирования не перпендикулярно к плоскости проекции):
- фронтальная изометрическая проекция;
- фронтальная диметрическая проекция;
- горизонтальная изометрическая проекция.

См. также

Проекция (геометрия)

Источники

↑ По ГОСТ 2.317-69 — Единая система конструкторской документации. Аксонометрические проекции.

Литература

Богданов В. Н., Малежик И. Ф., Верхола А. П. и др. Справочное руководство по черчению. — М.: Машиностроение, 1989. — С. 864. — ISBN 5-217-00403-7.
Под ред. Ишлинский А. Ю. Новый политехнический словарь. — М.: Большая Российская энциклопедия, 2003. — С. 671. — ISBN 5-7107-7316-6.
Фролов С. А. Начертательная геометрия. — 2-е изд., перераб. и доп. — М.: Машиностроение, 1983. — С. 240.

Ссылки

wikiredia.ru

Косоугольные проекции

Косоугольная проекция определяется углом наклона линии проецирования к плоскости проекции.

Отличие координат X,Y точки в исходной трехмерной системе и одноименных ее координат на плоскости проекции можно проанализировать на примере проекции единичного вектора по оси Z, которая приведена на Рис. 6.3 -62. На рисунке рассматривается случай, когда плоскость проекции совпадает с координатной плоскостью X,Y исходной трех мерной системы, из которой выполняется проецирование.

Рис. 6.3‑62

Проекцией конца единичного вектора, расположенного на оси Z (точки «т»), является точка на плоскости проекции, обозначенная как «тп», с координатами Px и Py. Эти координаты зависят от наклона линий проецирования, в частности от наклона линии проецирования, проходящей через конец рассматриваемого единичного вектора. С учетом этого, можно записать:

xтп = xт + Рx = 0 + Рx;

yтп = yт + Рy = 0 + Рx.

Величины Рx и Рy рассматриваются как отклонения, соответственно, по координатам X и Y при формировании косоугольной проекции точки.

Линии проецирования в рассматриваемой проекции параллельные, поэтому можно утверждать, что для всех точек исходной трех мерной системы с координатой по оси Z, равной «1», будет иметь место такие же отклонения по осям X и Y. Кроме того, очевидно при изменении координаты Z будут пропорционально изменяться отклонения по осям X и Y. Это позволяет записать для любой точки A(xA, yA, zA) исходной трех мерной системы ее координаты на плоскости проекции как:

xAп = xA + Рx z A;

xAп = yA + Рy z A.

Матрица, отражающая эту связь координат, имеет вид:

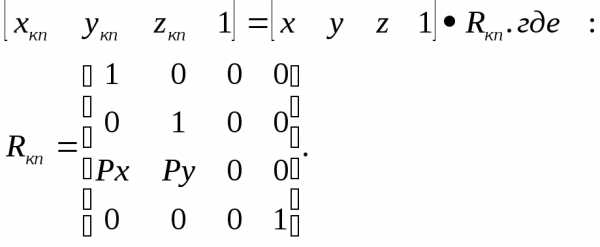
Для свободной косоугольной проекции имеет место:

Рx = сos 450;

Рy = sin 450.

Для кабинетной косоугольной проекии используется уменьшенный масштаб влияния координаты Z на смещение:

Рx = 0.5 сos 450;

Рy = 0.5 sin 450.

Аксонометрическая проекция

Простейшим случаем аксонометрической проекции является ортогональная проекция. Это такая аксонометрическая проекция, у которой плоскость проекции перпендикулярна одной из координатных осей исходной трех мерной системы координат. При этом возможны три случая.

Первый случай.

Плоскость проекции перпендикулярна оси Z и совпадает с координатной плоскостью XY. Проекция точки в этом случае определяется как:

Второй случай.

Плоскость проекции перпендикулярна оси X и совпадает с координатной плоскостью ZY. Проекция точки в этом случае определяется как:

Третий случай.

Плоскость проекции перпендикулярна оси Y и совпадает с координатной плоскостью XZ. Проекция точки в этом случае определяется как:

Общий случай аксонометрической проекции, когда плоскость проекции занимает произвольное положение в исходной трех мерной системе координат, иллюстрируется ниже приведенным рисунком (Рис. 6.4 -63).

Рис. 6.4‑63

На рисунке приведены следующие обозначения:

ПП – плоскость проецирования;
V – вектор направленности линий проецирования;
b – угол между осью Z и проекции вектора V на координатную плоскость XZ;
a – угол наклона вектора V к координатной плоскости XZ.

Найдем матрицу аксонометрической проекции Rпп, которая связывает координаты x, y, z точки в трех мерной системе и ее координаты xп, yп, zп на плоскости проекции ПП (координата zп на плоскости проекции равна 0):

Матицу Rпп можно найти, выполнив два этапа преобразований.

Первый этап.

От исходной системы координат перейдем в видовую систему координат, направление оси Zв которой совпадает с вектором проецирования V. Для этого исходную систему координат повернем на угол «в» относительно оси Y, а полученную систему координат повернем на угол «a» относительно оси X. Тогда матрица видового преобразования Rв рассчитывается следующим образом:

Полученная матрица обеспечивает переход к видовой системе координат, ось Z которой перпендикулярна плоскости проекции. Для такой видовой системы координат заданная проекция превращается в ортогональную проекцию с плоскостью проекции, перпендикулярной оси Z. Поэтому для получения матрицы аксонометрической проекции Rпп необходимо матрицу Rв умножить на матрицу Rопz ортогональной проекции на плоскость X,Y,0, т.е. имеем:

Полученная матрица обеспечивает преобразование для общего случая аксонометрической проекции, называемой триометрией, при которой углы «a» и «в» выбираются независимо друг от друга.

Для вывода зависимостей параметров аксонометрии для случаев диметрии и изометрии, рассмотрим аксонометрические проекции единичных векторов по координатным осям:

Используя матрицу аксонометрической проекции, запишем проекции этих векторов:

Возьмем диметрию, у которой координатные оси X и Y имеют одинаковые углы с осью Z. В этом случае можно утверждать, что проекции единичных векторов Ux и Uy, будут иметь одинаковую длину, а следовательно можно записать:

Uxп2 = Uуп2, т. е.

cos2b + sin2a sin2b = cos2a.

Разрешим это уравнение относительно «b», используя только функцию sin:

1-sin2b + sin2a sin2b =1- sin2a;

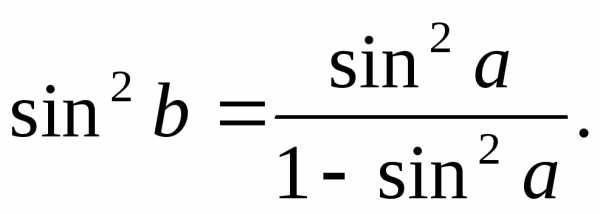(6.4-1)

Таким образом, при построении диметрии, задавая произвольный угол «а», необходимо по полченной формуле рассчитать угол «b».

Для изометрии проекции всех рассматриваемых единичных векторов будут одинаковыми. Поэтому можно записать:

Uzп2 = Uуп2, т. е.

sin2b + sin2a cos2b = cos2a.

Разрешим это уравнение относительно «b», используя только функцию sin:

sin2b + sin2a (1-sin2b) = 1-sin2a,

(6.4-2)

На основании выражений (6.4-1) и (6.4-2), можем записать:

sin2a = 1- 2sin2a, откуда:

sin2a = 1/3, а .

Подставляя полученное значение для sin a в выражение (6.4-1), будем иметь:

Из этого следует, что для задания изометрии, необходимо взять в качестве значений для ее параметров «а» и «в» выше рассчитанные значения.

studfiles.net

Косоугольные проекции

Косоугольная проекция определяется углом наклона линии проецирования к плоскости проекции.

Рис. 6.3‑62

xтп = xт + Рx = 0 + Рx;

yтп = yт + Рy = 0 + Рx.

xAп = xA + Рx z A;

xAп = yA + Рy z A.

Матрица, отражающая эту связь координат, имеет вид:

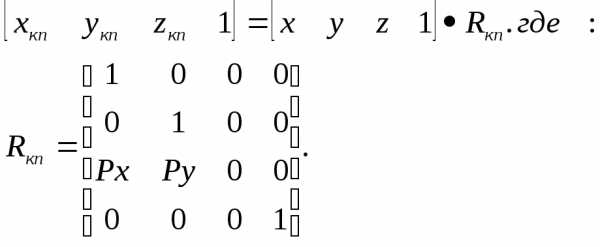
Для свободной косоугольной проекции имеет место:

Рx = сos 450;

Рy = sin 450.

Для кабинетной косоугольной проекии используется уменьшенный масштаб влияния координаты Z на смещение:

Рx = 0.5 сos 450;

Рy = 0.5 sin 450.

Аксонометрическая проекция

Первый случай.

Второй случай.

Третий случай.

Рис. 6.4‑63

На рисунке приведены следующие обозначения:

ПП – плоскость проецирования;
V – вектор направленности линий проецирования;
b – угол между осью Z и проекции вектора V на координатную плоскость XZ;
a – угол наклона вектора V к координатной плоскости XZ.

Матицу Rпп можно найти, выполнив два этапа преобразований.

Первый этап.

Используя матрицу аксонометрической проекции, запишем проекции этих векторов:

Uxп2 = Uуп2, т. е.

cos2b + sin2a sin2b = cos2a.

Разрешим это уравнение относительно «b», используя только функцию sin:

1-sin2b + sin2a sin2b =1- sin2a;

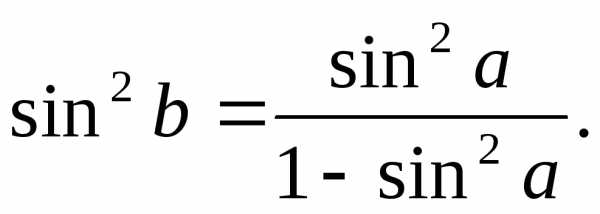(6.4-1)

Для изометрии проекции всех рассматриваемых единичных векторов будут одинаковыми. Поэтому можно записать:

Uzп2 = Uуп2, т. е.

sin2b + sin2a cos2b = cos2a.

Разрешим это уравнение относительно «b», используя только функцию sin:

sin2b + sin2a (1-sin2b) = 1-sin2a,

(6.4-2)

На основании выражений (6.4-1) и (6.4-2), можем записать:

sin2a = 1- 2sin2a, откуда:

sin2a = 1/3, а .

Подставляя полученное значение для sin a в выражение (6.4-1), будем иметь:

studfiles.net

Косоугольная проекция Википедия

Проецирование параллелепипеда на плоскость П'.

Предмет с системой координат, к которой он отнесён, проецируют на произвольную плоскость (картинная плоскость аксонометрической проекции) таким образом, чтобы эта плоскость не совпадала с его координатной плоскостью. В этом случае получаются две взаимосвязанные проекции одной фигуры на одну плоскость, что позволяет восстановить положение в пространстве, получив наглядное изображение предмета. Так как картинная плоскость не параллельна ни одной из координатных осей, то имеются искажения отрезков по длине параллельных координатным осям. Это искажение может быть равным по всем трём осям — изометрическая проекция, одинаковыми по двум осям — диметрическая проекция и с искажениями разными по всем трём осям — триметрическая проекция.

Стандартизированные аксонометрические проекции [1][ | код]

Аксонометрическая проекция

прямоугольная проекция (направление проецирования перпендикулярно к плоскости проекции):
косоугольная проекция (направление проецирования не перпендикулярно к плоскости проекции):
- фронтальная изометрическая проекция;
- фронтальная диметрическая проекция;
- горизонтальная изометрическая проекция.

См. также[ | код]

Проекция (геометрия)

Источники[ | код]

↑ По ГОСТ 2.317-69 — Единая система конструкторской документации. Аксонометрические проекции.

Литература[

ru-wiki.ru