Прямоугольная изометрия. Прямоугольная изометрия
Прямоугольная изометрия
Плоскость Р наклонена к Оxyz под равными углами, отсюда следует следующее расположение осей (рис.20).
Коэффициенты искажения по всем осям одинаковые и равны 0,82 (k = m = n =0,82). Однако ГОСТ 2.317-69 рекомендует использовать приведенные коэффициенты искажения, равные 1 (k = m = n = 1), т. е. отрезки, параллельные осям, откладываются в натуральную величину. Изображение получается увеличенным, но пропорциональным.
Рис. 20
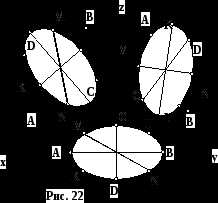
Аксонометрической проекцией окружности на любую плоскость проекций в любом виде аксонометрии будет эллипс. Эллипс – это плоская замкнутая кривая, которая характеризуется рядом параметров. ГОСТ 2.317-69 разрешает строить эллипсы по самым простым – величинам большой (AB) и малой (CD) осей эллипса (рис. 21).
В прямоугольной изометрии на любую плоскость проекций окружность проецируется следующим образом (рис. 22):
Большая ось эллипса (AB) перпендикулярна оси координат отсутствующей в данной плоскости. Например, при проецировании окружности на горизонтальную плоскость проекций большая ось перпендикулярна оси z (AB ┴ oz).
Малая ось эллипса перпендикулярна большой (CD ┴ AB).
AB = 1,22 d
CD = 0,71 d
где d-диаметр исходной окружности.
Поскольку построить гладкий эллипс по четырем точкам достаточно сложно, можно провести в окружности диаметры, параллельные осям координат, сопряженные с ними - сопряженные диаметры. Например, для окружности, проецируемой на горизонтальную плоскость проекций, диаметры, параллельные осям x и y.
KL // ox, KL = 1 d
MN // oy, MN = 1 d
Косоугольная диметрия
По ГОСТ 2.317-69 расположение осей координат следующее: ось x – горизонтальна, ось z – вертикальна, ось y – отклонена от горизонтали на 45о. Устанавливаются следующие приведенные коэффициенты искажения вдоль:
- оси x – 1, k = 1;
- оси z – 1, n = 1;
- оси y – 1, m = 0,5
При проецировании на фронтальную плоскость сохраняются не только линейные, но и угловые размеры. Это значит, что плоские фигуры, параллельные фронтальной плоскости, проецируются на нее в натуральную форму, т. е. без искажения. Например, окружность проецируется на фронтальную плоскость, как окружность.
На горизонтальную и профильную плоскости проекций окружности проецируются, как эллипсы. При проецировании на горизонтальную плоскость проекций большая ось эллипса отклонена от горизонтали в сторону оси x на угол 7о14′. При проецировании на профильную плоскость проекций большая ось эллипса отклонена от вертикали в сторону оси z на угол 7о14′. Такой угол определяется из прямоугольного треугольника с соотношением сторон 1 : 8 (рис. 23).
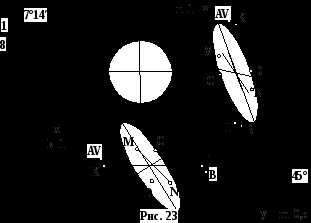
Коэффициенты искажения по большой и малой осям эллипса по отношению к диаметру окружности при проецировании на горизонтальную и профильную плоскости проекций:
AB = 1,07 d;
CD ┴ AB, CD = 0,33 d.
Для горизонтальной проекции:
KL // ox, KL = 1 d;
MN //oy, MN = 0,5d.
Для профильной проекции:
KL // oz, KL = 1 d.
MN //oy, MN = 0,5 d.
Прямоугольная диметрия
Из трех стандартных аксонометрических проекций прямоугольная диметрия наиболее трудоемка, но и наиболее наглядна (рис. 24).
Для этой проекции приняты следующее расположение осей координат и приведенные коэффициенты искажения:
– ось x отклонена от горизонтали на угол 7о10′. Такой угол с достаточной точностью определяется из прямоугольного треугольника с соотношением катетов 1 : 8. Приведенный коэффициент искажения – k = 1;
– ось y отклонена от горизонтали на угол 41о25′. Такой угол строится в прямоугольном треугольнике с соотношением сторон 7 : 8. приведенный коэффициент искажения – m = 0,5;
– ось z направлена вертикально. Приведенный коэффициент искажения – n = 1.
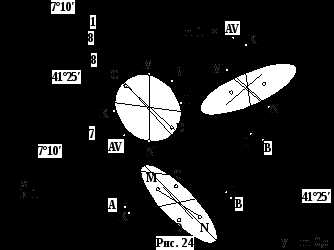
На все три плоскости проекций окружности проецируются, как эллипсы.
При проецировании на горизонтальную плоскость проекций:
– большая ось эллипса AB расположена горизонтально.
AB = 1,06 d;
– малая ось CD перпендикулярна AB. CD = 0,35 d;
– сопряженный диаметр KL // OX. KL = 1 d;
– сопряженный диаметр MN // OY. MN = 0,5 d;
При проецировании на профильную плоскость проекций:
– большая ось эллипса AB расположена перпендикулярно оси X. AB = 1,06 d;
– малая ось CD перпендикулярна AB. CD = 0,35 d;
– сопряженный диаметр KL // OZ. KL = 1 d;
– сопряженный диаметр MN // OY. MN = 0,5 d.
При проецировании на фронтальную плоскость проекций:
– большая ось эллипса AB расположена перпендикулярно оси Y. AB = 1,06 d;
– малая ось CD перпендикулярна AB. CD = 0,95 d;
– сопряженный диаметр KL // OX. KL = 1 d;
studfiles.net
Прямоугольная изометрия
⇐ ПредыдущаяСтр 9 из 12Следующая ⇒
В изометрии все оси наклонены к аксонометрической плоскости под одним и тем же углом, следовательно угол между осями (120° ) и коэффициент искажения будет одинаков. Выбираем масштаб 1 : 0,82=1,22; М 1,22 : 1.
Для удобства построения пользуются приведенными коэффициентами и тогда на всех осях и линиях им параллельных откладываются натуральные размеры. Изображения таким образом становятся больше, но на наглядности это не отражается.
Выбор вида аксонометрии зависит от формы изображаемой детали. Проще всего строить прямоугольную изометрию, поэтому такие изображения встречаются чаще. Однако, при изображении деталей, включающих четырехугольные призмы и пирамиды, их наглядность уменьшается. В этих случаях лучше выполнять прямоугольную диметрию.
Косоугольную диметрию следует выбирать для деталей, имеющих большую длину при небольшой высоте и ширине (типа вала) или когда одна из сторон детали содержит наибольшее число важных особенностей.
В аксонометрических проекциях сохраняются все свойства параллельных проекций.
Рассмотрим построение плоской фигуры АВСDE.
Рис.10.4
Прежде всего построим оси в аксонометрии. На рис.10.4 представлено два способа построения аксонометрических осей в изометрии. На рис.10.4 а показано построение осей при помощи циркуля, а на рис.10.4б - построение при помощи равных отрезков.
Далее рассмотрим построение плоской фигуры АВСDE на плоском чертеже (рис.10.5а) и в аксонометрии (рис.10.5б)
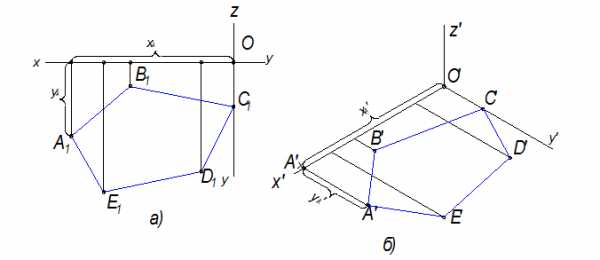Рис.10.5
Фигура АВСDЕ лежит в горизонтальной плоскости проекций, которая ограничена осями ОХ и ОY (рис.10.5а). Строим эту фигуру в аксонометрии (рис.10.5б).
Каждая точка, лежащая в плоскости проекций, сколько имеет координат? Две.
Точка, лежащая в горизонтальной плоскости - координаты Х и Y.
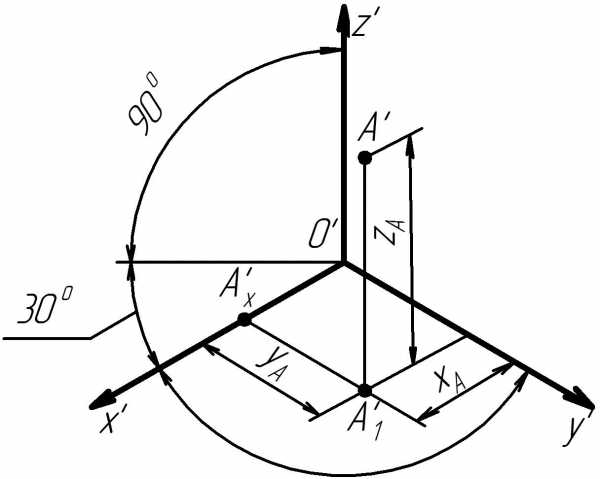
Рассмотрим построение т.А. С какой координаты начнем построение? С координаты ХА.
Для этого замеряем на ортогональном чертеже величину ОАХ и откладываем на оси Х', получим точку АХ'. АХА1 какой оси параллельна? Оси Y. Значит из т. АХ' проводим прямую параллельную оси Y' и откладываем на ней координату YA. Полученная точка А' и будет аксонометрической проекцией т.А.
Аналогично строятся все остальные точки. Точка С лежит на оси ОY, значит имеет одну координату.
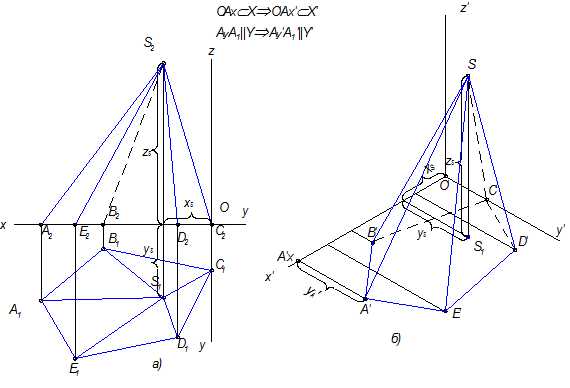
Рис.10.6
На рисунке 10.6 задана пятигранная пирамида, у которой основанием является этот же пятиугольник АВСDЕ. Что нужно достроить, чтобы получилась пирамида? Надо достроить точку S, которая является ее вершиной.
Точка S- точка пространства, поэтому имеет три координаты ХS, YS и ZS. Сначала строится вторичная проекция S (S1 ), а затем все три размера переносятся с ортогонального чертежа. Соединив S' c A', B', C', D' и E', получим аксонометрическое изображение объемной фигуры - пирамиды.
©2015 arhivinfo.ru Все права принадлежат авторам размещенных материалов.
arhivinfo.ru
Прямоугольная изометрическая проекция - Технические чертежи
Прямоугольная изометрическая проекцияКатегория:
Технические чертежи
Положение осей в прямоугольной изометрической проекции следующее: ось oz располагают вертикально, а оси ох и оу— под углом 120° к ней (рис. 1). Оси симметрии или ребра изделия располагают параллельно направлению осей ох, оу и oz.
При построении изометрической проекции изделия линейные размеры его откладывают обычно в натуральную величину по всем трем осям. Получающееся изображение будет несколько увеличенным по отношению к его натуральным размерам (в 1,22 раза). Чтобы получить в изометрической проекции изображение, равное натуральной величине предмета, применяют коэффициент искажения по всем трем осям ox, оу, oz, равный 0,82. Ввиду одинакового коэффициента искажения по всем трем аксонометрическим осям этот вид аксонометрической проекции называется изометрической проекцией.
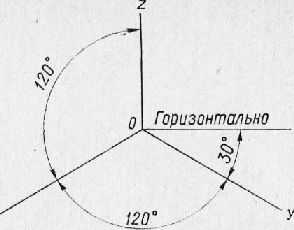
Рис. 1. Расположение аксонометрических осей в прямоугольной изометрической проекции.
Для представления о направлении осей эллипсов предположим, что дана изометрическая проекция куба с вписанными в его грани окружностями.
Из рисунка видно, что всякую окружность, находящуюся на горизонтальной поверхности, изображают в виде эллипса с горизонтально расположенной большой осью и вертикально расположенной малой. Кроме того, всякую окружность, находящуюся на передней или боковой поверхности, изображают в виде эллипса с большой осью, направленной под углом 60° к горизонтали. При этом во всех случаях большую ось эллипса располагают по большой диагонали ромба, а малую ось — по его малой диагонали.
Эллипсы в изометрической проекции можно заменить овалами. Строят ромб с острым углом 60° и со стороной, равной диаметру окружности. Из точки D опускают перпендикуляры Dn и Dnx на стороны АС и ВС ромба. Получают точки сопряжения п и п%. Перпендикуляры Dn и Dri]_ пересекают большую ось (диагональ) ромба в точках Ох и 02.
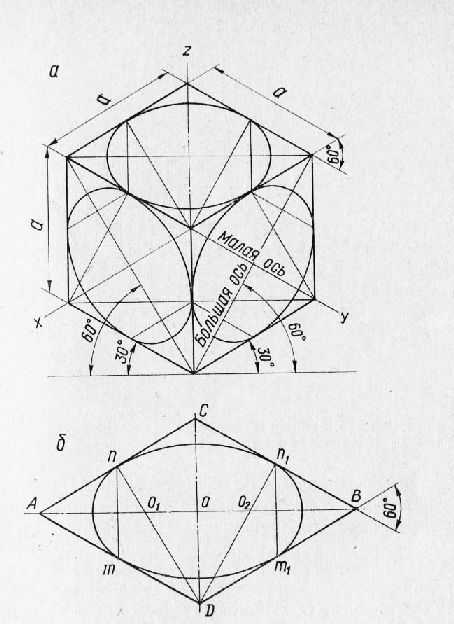
Рис. 2. Изометрические проекции куба со вписанными в его грани окружностями: а —окружности изображены в виде эллипсов; б — эллипсы заменены овалами.
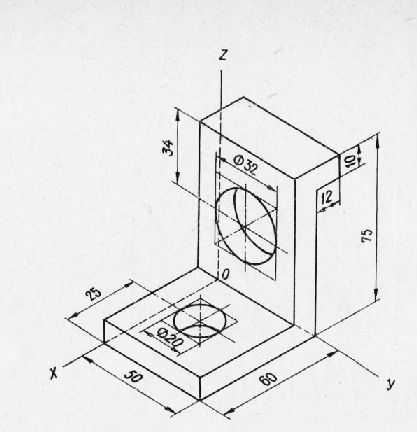
Рис. 3. Пример построения изометрической проекции.
На рис. 3 показано построение изометрической проекции угольника с двумя цилиндрическими отверстиями, расположенными в различных гранях. Сначала строят оси изометрической проекции и на них откладывают размеры длины, ширины и высоты угольника. На оси ох откладывают размер длины 60 мм, на оси оу — размер ширины 50 мм и на оси oz — размер высоты 75 мм. Прямолинейные очертания угольника изображаются контурными прямыми параллельно этим осям.
Для изображения отверстий, имеющихся в угольнике, сперва определяют положение их центров. Затем строят ромбы со сторонами, параллельными аксонометрическим осям и равными диаметру отверстий. В эти ромбы вписывают овалы, изображающие отверстия.
Построение овалов осуществляют согласно рис. 2, б. Так, отверстие 020 мм, расположенное на горизонтальной грани угольника, изображается овалом, вписанным в ромб, стороны которого параллельны осям охи оу и равны 20 мм. Овал, изображающий отверстие 0 32 мм, расположенное на вертикальной грани угольника, вписывается в ромб, стороны которого равны 32 мм и расположены параллельно осям оу и oz. Подобные построения могут быть применены и для деталей более сложных форм.
Читать далее:
Прямоугольная диметрическая проекция
Статьи по теме:
Прямоугольная изометрическая проекция
Наибольшее распространение получили прямоугольные изометрические проекции, поэтому рассмотрим их более детально.
Положение аксонометрических осей приведено на рис. 70 Ось z' расположена вертикально, а оси х' и у' составляют с осью z' углы по 120°.
Показатели искажения для всех осей одинаковы и равны 0,82(по теории), но для удобства p = k = q = 1.
| Рис. 70 Построение точки в прямоугольной изометрии |
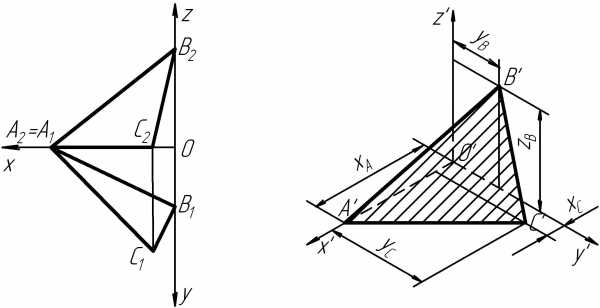
а б
Рис. 71 Построение плоскости треугольника в прямоугольной изометрии
При построении аксонометрических проекций предметов, имеющих плоскости симметрии, за координатные плоскости принимают плоскости симметрии предметов.
Например, на рис. 72,а за координатные плоскости хОz и yOz приняты плоскости симметрии правильной шестигранной призмы.
Построим приведенную изометрическую проекцию призмы. Построение начнем с нижнего основания призмы, лежащего в плоскости хОу (рис. 72,б). Находим изометрические проекции точек 1 и 2,принадлежащих оси х, и точек 3 и 4,принадлежащих оси у. Через найденные точки 3' и 4'проводим линии, параллельные аксонометрической оси х', и откладываем на них координаты х точек 5,6,7 и 8.Из точек 1', 2', 5', 6', 7', 8'проводим вертикальные линии, параллельные оси z', и откладываем на них отрезки, равные по величине высоте призмы. Соединив найденные точки прямыми, получим приведенную изометрическую проекцию призмы. Можно начать построение и с верхнего основания призмы.
При построении аксонометрических проекций следует помнить, что координаты точек или отрезки прямых можно откладывать только по осям или по линиям, параллельным осям, так как отрезки, не параллельные ни одной из осей координат, проецируются на плоскость аксонометрических проекций с иным искажением.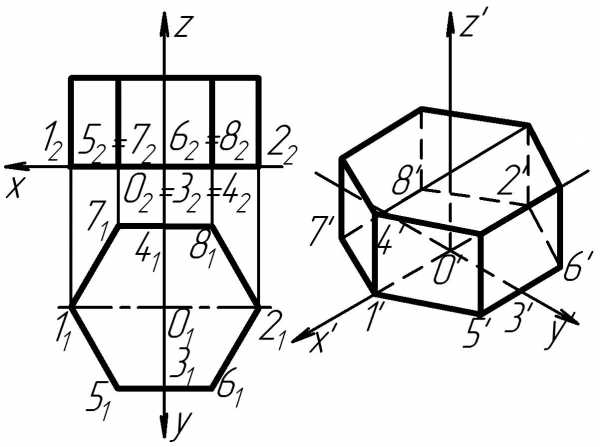
а б
Рис. 72 Построение правильной шестигранной призмы в прямоугольной изометрии
Похожие статьи:
poznayka.org
Прямоугольная изометрия
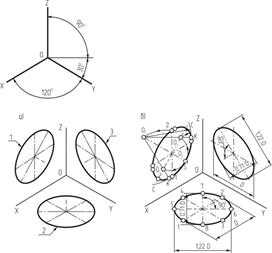
⇐ ПредыдущаяСтр 2 из 4Следующая ⇒Прямоугольная изометрическая проекция образуется при прямоугольном проецировании предмета и связанных с ним координатных осей на плоскость аксонометрических проекций П', одинаково наклоненную к каждой координатной оси.
В этом случае все три коэффициента искажения будут равны между собой, так как равны углы наклона координатных осей к плоскости П', то есть u = v = w.
Углы между аксонометрическими осями будут равны 120° (рис. 2, а). Ось Z всегда проводят вертикально. Оси Х и У располагают под углами 30° к линии горизонта.
Согласно основной формуле аксонометрии (2), действительные (точные) коэффициенты искажения для прямоугольной изометрической проекции u = v = w = 0,82.
Следовательно, при образовании данной проекции натуральные размеры вдоль координатных осей сокращаются в ≈ 0,82 раза.
В практике (ГОСТ 2.317–69) построения аксонометрических изображений дробные коэффициенты заменяют приведенными коэффициентами искажения (целыми числами) – единицами: U= V = = W = 1.
В этом случае изображение получается увеличенным в 1,22 раза.
Аксонометрический масштаб такого изображения 1,22 : 1.
Равные окружности, расположенные в координатных или параллельных им плоскостях, будут проецироваться в равные по величине эллипсы (рис. 2, б).
а) б)
Рис. 2
Длины осей эллипсов 1, 2, 3 при диаметре окружности D в зависимости от принятых коэффициентов искажения приведены в табл. 1.
Таблица 1
| Показатели | Действительные | Приведенные |
| Коэффициент искажения | 0,82 | |
| Большая ось эллипса | D | 1,22 D |
| Малая ось эллипса | 0,58D | 0,71 D |
mykonspekts.ru
