Open Library - открытая библиотека учебной информации. Развертка четырехугольной призмы
Развертка поверхности прямой четырехугольной призмы
Всякое разное Развертка поверхности прямой четырехугольной призмы
Количество просмотров публикации Развертка поверхности прямой четырехугольной призмы - 17
| Наименование параметра | Значение |
| Тема статьи: | Развертка поверхности прямой четырехугольной призмы |
| Рубрика (тематическая категория) | Всякое разное |
Полная развертка такой призмы (рис. 9.1) состоит из четырех прямоугольников, представляющих в истинном виде боковые грани призмы, и двух четырехугольников – её верхнᴇᴦο и нижнᴇᴦο оснований.
Взяв произвольную прямую (рис. 9.2), отложим на ней произвольно отрезки, равные сторонам основания призмы AB, BC, CD, DA, истинные длины которых имеем на рис. 9.1. Далее проведя в точках A, B, C и D к прямой перпендикуляры, отложим на них длину боковых ребер (высоту) призмы и соединим полученные точки прямой. Построенный прямоугольник представит развертку боковой поверхности призмы.
Пристроив к однои̌ из граней верхнее и нижнее основания призмы, получим полную развертку призмы.
Пересечем ту же призму фронтально проецирующей плоскостью a (рис. 9.1) и нанесем на развертку линию, по которой плоскость a пересечет поверхность призмы.
Для ϶того будет достаточно отметить на развертке точки 1, 2, 3 и 4, в которых боковые ребра призмы пересекаются плоскостью a, и каждые две смежные точки соединить прямой – ϶то будут линии, по которым грани призмы пересекаются той же плоскостью.
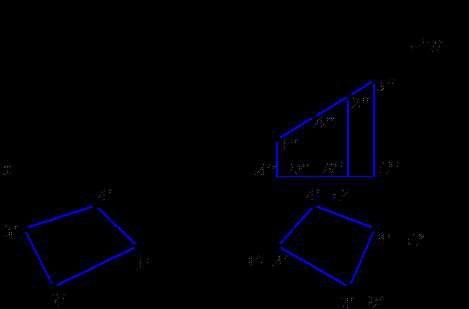
Рис. 9.1
Для получения полнои̌ развертки усеченнои̌ призмы необходимо выяснить способом совмещения истинный вид сечения и построить фигуру сечения на развертке к однои̌ из граней призмы, что и выполнено на рис. 9.2.
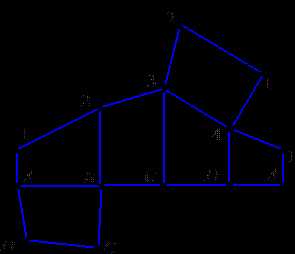
Рис. 9.2
Развертка поверхности прямой четырехугольной призмы - понятие и виды. Классификация и особенности категории "Развертка поверхности прямой четырехугольной призмы"2017-2018.
referatwork.ru
Развертка поверхности прямой четырехугольной призмы
РАЗВЕРТЫВАНИЕ ПОВЕРХНОСТЕЙ
Разверткой называется плоская фигура, получаемая путем совмещения с плоскостью чертежа поверхности тела.
Построение разверток имеет большое значение в таких областях техники, как котлостроение, судостроение, кровельное и жестяничное дело, продукция которых изготовляется из листового материала.
Точные развертки могут быть построены лишь для линейчатых поверхностей, смежные положения образующих которых параллельны (цилиндрическая поверхность) или пересекаются (коническая поверхность).
Для поверхностей нелинейчатых, образующей которых является кривая линия (например, сферическая поверхность), можно построить развертки лишь приближенные. С этой целью такие поверхности разбиваются на небольшие элементы и каждая такая часть кривой поверхности заменяется плоскостью. Это означает, что данная кривая поверхность заменяется вписанным в нее многогранником, развертка которого приближенно принимается за развертку кривой поверхности.
Полная развертка такой призмы (рис. 9.1) состоит из четырех прямоугольников, представляющих в истинном виде боковые грани призмы, и двух четырехугольников – ее верхнего и нижнего оснований.
Взяв произвольную прямую (рис. 9.2), отложим на ней произвольно отрезки, равные сторонам основания призмы AB, BC, CD, DA, истинные длины которых имеем на рис. 9.1. Затем проведя в точках A, B, C и D к прямой перпендикуляры, отложим на них длину боковых ребер (высоту) призмы и соединим полученные точки прямой. Построенный прямоугольник представит развертку боковой поверхности призмы.
Пристроив к одной из граней верхнее и нижнее основания призмы, получим полную развертку призмы.
Пересечем ту же призму фронтально проецирующей плоскостью a (рис. 9.1) и нанесем на развертку линию, по которой плоскость a пересечет поверхность призмы.
Для этого будет достаточно отметить на развертке точки 1, 2, 3 и 4, в которых боковые ребра призмы пересекаются плоскостью a, и каждые две смежные точки соединить прямой – это будут линии, по которым грани призмы пересекаются той же плоскостью.

Рис. 9.1
Для получения полной развертки усеченной призмы необходимо определить способом совмещения истинный вид сечения и построить фигуру сечения на развертке к одной из граней призмы, что и выполнено на рис. 9.2.

Рис. 9.2
studlib.info
Развертка поверхности прямой четырехугольной призмы
Изобретательство Развертка поверхности прямой четырехугольной призмы
просмотров - 360
РАЗВЕРТЫВАНИЕ ПОВЕРХНОСТЕЙ
Разверткой принято называть плоская фигура, получаемая путем совмещения с плоскостью чертежа поверхности тела.
Построение разверток имеет большое значение в таких областях техники, как котлостроение, судостроение, кровельное и жестяничное дело, продукция которых изготовляется из листового материала.
Точные развертки бывают построены лишь для линейчатых поверхностей, смежные положения образующих которых параллельны (цилиндрическая поверхность) или пересекаются (коническая поверхность).
Для поверхностей нелинейчатых, образующей которых является кривая линия (к примеру, сферическая поверхность), можно построить развертки лишь приближенные. С этой целью такие поверхности разбиваются на небольшие элементы и каждая такая часть кривой поверхности заменяется плоскостью. Это означает, что данная кривая поверхность заменяется вписанным в нее многогранником, развертка которого приближенно принимается за развертку кривой поверхности.
Полная развертка такой призмы (рис. 9.1) состоит из четырех прямоугольников, представляющих в истинном виде боковые грани призмы, и двух четырехугольников – ее верхнего и нижнего оснований.
Взяв произвольную прямую (рис. 9.2), отложим на ней произвольно отрезки, равные сторонам основания призмы AB, BC, CD, DA, истинные длины которых имеем на рис. 9.1. Затем проведя в точках A, B, C и D к прямой перпендикуляры, отложим на них длину боковых ребер (высоту) призмы и соединим полученные точки прямой. Построенный прямоугольник представит развертку боковой поверхности призмы.
Пристроив к одной из граней верхнее и нижнее основания призмы, получим полную развертку призмы.
Пересечем ту же призму фронтально проецирующей плоскостью a (рис. 9.1) и нанесем на развертку линию, по которой плоскость a пересечет поверхность призмы.
Для этого будет достаточно отметить на развертке точки 1, 2, 3 и 4, в которых боковые ребра призмы пересекаются плоскостью a, и каждые две смежные точки соединить прямой - ϶ᴛᴏ будут линии, по которым грани призмы пересекаются той же плоскостью.
Рис. 9.1
Для получения полной развертки усеченной призмы крайне важно определить способом совмещения истинный вид сечения и построить фигуру сечения на развертке к одной из граней призмы, что и выполнено на рис. 9.2.
Рис. 9.2
Читайте также
РАЗВЕРТЫВАНИЕ ПОВЕРХНОСТЕЙ Разверткой называется плоская фигура, получаемая путем совмещения с плоскостью чертежа поверхности тела. Построение разверток имеет большое значение в таких областях техники, как котлостроение, судостроение, кровельное и... [читать подробенее]
Построение развертки поверхности прямой четырехугольной призмы
Изобретательство Построение развертки поверхности прямой четырехугольной призмы
просмотров - 84
Развертки
Лекция № 16
Тема лекции: Определение развертки, развертываемые и неразвертываемые поверхности. Построение развертки поверхностей призмы, пирамиды. (раздел 5)
1. Определение развертки, развертываемые и неразвертываемые поверхности.
2. Построение развертки поверхности призмы.
3. Построение развертки поверхности пирамиды.
Разверткой принято называть плоская фигура, получаемая путем совмещения с плоскостью чертежа поверхности тела.
Построение разверток имеет большое значение в таких областях техники, как котлостроение, судостроение, кровельное и жестяное дело, продукция которых изготовляется из листового материала.
Точные развертки бывают построены лишь для линейчатых поверхностей, смежные положения образующих которых параллельны (цилиндрическая поверхность) или пересекаются (коническая поверхность).
Для поверхностей нелинейчатых, образующей которых является кривая линия (к примеру, сферическая поверхность), можно построить развертки лишь приближенные. С этой целью такие поверхности разбиваются на небольшие элементы, и каждая такая часть кривой поверхности заменяется плоскостью. Это означает, что данная кривая поверхность заменяется вписанным в нее многогранником, развертка которого приближенно принимается за развертку кривой поверхности.
Полная развертка такой призмы (рис. 16.1) состоит из четырех прямоугольников, представляющих в истинном виде боковые грани призмы, и двух четырехугольников – ее верхнего и нижнего оснований.
Взяв произвольную прямую (рис. 16.2), отложим на ней произвольно отрезки, равные сторонам основания призмы AB, BC, CD, DA, истинные длины которых имеем на рис. 16.1. Затем, проведя в точках A, B, C и D к прямой перпендикуляры, отложим на них длину боковых ребер (высоту) призмы и соединим полученные точки прямой. Построенный прямоугольник представит развертку боковой поверхности призмы.
Пристроив к одной из граней верхнее и нижнее основания призмы, получим полную развертку призмы.
Пересечем ту же призму фронтально проецирующей плоскостью a (рис. 16.1) и нанесем на развертку линию, по которой плоскость a пересечет поверхность призмы.
Для этого будет достаточно отметить на развертке точки 1, 2, 3 и 4, в которых боковые ребра призмы пересекаются плоскостью a, и каждые две смежные точки соединить прямой - ϶ᴛᴏ будут линии, по которым грани призмы пересекаются той же плоскостью.
Для получения полной развертки усеченной призмы крайне важно определить способом совмещения истинный вид сечения и построить фигуру сечения на развертке к одной из граней призмы, что и выполнено на рис. 16.2.
Читайте также
Развертки Лекция № 16 Тема лекции: Определение развертки, развертываемые и неразвертываемые поверхности. Построение развертки поверхностей призмы, пирамиды. (раздел 5) 1. Определение развертки, развертываемые и неразвертываемые поверхности. 2. Построение... [читать подробенее]
oplib.ru
Развертка поверхности прямой четырехугольной призмы
Изобретательство Развертка поверхности прямой четырехугольной призмы
просмотров - 359
РАЗВЕРТЫВАНИЕ ПОВЕРХНОСТЕЙ
Разверткой принято называть плоская фигура, получаемая путем совмещения с плоскостью чертежа поверхности тела.
Построение разверток имеет большое значение в таких областях техники, как котлостроение, судостроение, кровельное и жестяничное дело, продукция которых изготовляется из листового материала.
Точные развертки бывают построены лишь для линейчатых поверхностей, смежные положения образующих которых параллельны (цилиндрическая поверхность) или пересекаются (коническая поверхность).
Для поверхностей нелинейчатых, образующей которых является кривая линия (к примеру, сферическая поверхность), можно построить развертки лишь приближенные. С этой целью такие поверхности разбиваются на небольшие элементы и каждая такая часть кривой поверхности заменяется плоскостью. Это означает, что данная кривая поверхность заменяется вписанным в нее многогранником, развертка которого приближенно принимается за развертку кривой поверхности.
Полная развертка такой призмы (рис. 9.1) состоит из четырех прямоугольников, представляющих в истинном виде боковые грани призмы, и двух четырехугольников – ее верхнего и нижнего оснований.
Взяв произвольную прямую (рис. 9.2), отложим на ней произвольно отрезки, равные сторонам основания призмы AB, BC, CD, DA, истинные длины которых имеем на рис. 9.1. Затем проведя в точках A, B, C и D к прямой перпендикуляры, отложим на них длину боковых ребер (высоту) призмы и соединим полученные точки прямой. Построенный прямоугольник представит развертку боковой поверхности призмы.
Пристроив к одной из граней верхнее и нижнее основания призмы, получим полную развертку призмы.
Пересечем ту же призму фронтально проецирующей плоскостью a (рис. 9.1) и нанесем на развертку линию, по которой плоскость a пересечет поверхность призмы.
Для этого будет достаточно отметить на развертке точки 1, 2, 3 и 4, в которых боковые ребра призмы пересекаются плоскостью a, и каждые две смежные точки соединить прямой - ϶ᴛᴏ будут линии, по которым грани призмы пересекаются той же плоскостью.
Рис. 9.1
Для получения полной развертки усеченной призмы крайне важно определить способом совмещения истинный вид сечения и построить фигуру сечения на развертке к одной из граней призмы, что и выполнено на рис. 9.2.
Рис. 9.2
Читайте также
РАЗВЕРТЫВАНИЕ ПОВЕРХНОСТЕЙ Разверткой называется плоская фигура, получаемая путем совмещения с плоскостью чертежа поверхности тела. Построение разверток имеет большое значение в таких областях техники, как котлостроение, судостроение, кровельное и... [читать подробенее]
oplib.ru
5.5. Развертки многогранников
Совмещение всех граней многогранника с одной плоскостью путем последовательного вращения их вокруг ребер называется разверткой многогранника.
Все грани многогранника на развертке изображаются в натуральной величине. Поэтому построение развертки сводится к построению натуральных величин граней многогранника. Их расположение и последовательность могут быть различны.
Чтобы получить развертку выпуклого многогранника нужно на его поверхности провести линию разреза, которая должна удовлетворять трем условиям:
1) проходить через все вершины выпуклого многогранника;
2) не должна быть замкнутой;
3) состоять из связанных между собой участков (линия разреза должна представлять собой одну линию).
Задача: Построить развертку прямой четырехугольной усеченной призмы, с основанием на плоскости Н, (рис. 5.10).
Решение.
1. Определяем линию разреза многогранника для построения развертки (САВD4312).
2. Устанавливаем, что нижнее основание (АВСD) призмы изображено в натуральную величину на горизонтальной плоскости проекций, а ребра призмы изображены в натуральную величину на фронтальной плоскости проекций.
3. Определяем натуральную величину верхнего основания (сечения) призмы методом вращения вокруг проецирующей оси проходящей через точку 1 перпендикулярно плоскости V: (1н,2н,3н,4н - натуральная величина сечения).

Рис. 5.10 – Построение развертки прямой четырехугольной
Усеченной призмы
4. Строим развертку призмы. На горизонтальной линии отложим отрезки DВ = DнВн; ВА = ВнАн; АС = АнСн; СD = СнDн (ширина каждой из боковых граней).
На перпендикулярах к этим отрезкам откладываются величины ребер D4=Dv4v; В2=Вv2v; А1=Аv1v; С3=СvЗv.
Многоугольник D42134D представляет собой развертку боковой поверхности призмы. Нижнее основание призмы, равное горизонтальной проекции его (АнВнDнСн) пристраивается, например, к стороне СD развертки боковой поверхности призмы. Натуральная величина основания (1н2’н3’н4’н) примыкает к развертке боковой поверхности стороной 24.
Глава 6. Кривые линии
6.1. Основные определения и проекции кривых
Кривая в начертательной геометрии определяется как множество последовательных положений точки, непрерывно перемещающейся в пространстве с изменением направления движения. Если движение точки изменяется по определенному закону, то кривая называется закономерной. Если движение произвольное, то получается кривая общего вида.
Кривые линии могут быть плоскими и пространственными. У плоской кривой все точки инцидентны некоторой плоскости. Закономерные плоские кривые могут определяться своими уравнениями - алгебраическими (окружность, гипербола, эллипс, парабола и др.) или трансцендентными (спираль Архимеда, синусоида). Кривые общего вида могут задаваться только графически. Степень уравнения алгебраической кривой определяет ее порядок. Графически порядок кривой определяется количеством точек пересечения с прямой, причем точки берутся как действительные, так и мнимые. Порядок кривой сохраняется и у проекций кривой. Если спроецировать кривую b на плоскость Н по направлению S, то на ней получится проекция кривой bH, обладающая всеми свойствами, которые сохраняются при параллельном проецировании (см. рис.6.1).

Рис. 6.1 – Проекция кривой Рис. 6.2 – Касательная к
b на плоскость Н кривой b
Касательной t к плоской кривой b в точке A называется предельное положение секущей t1, когда точки A1 и A2, оставаясь на кривой b, стремятся к точке A (рис.6.2).
Нормалью n к кривой b в точке A называют прямую инцидентную плоскости P и перпендикулярную к касательной t в этой точке. К плоской кривой может быть проведена только одна нормаль. К пространственной кривой в данной точке можно провести бесчисленное множество перпендикуляров к касательной, которые определяют нормальную плоскость.
Касательная к кривой в заданной точке проецируется в касательные к ее проекциям (tH; tv). Проекции нормали (nH; nV) (рис.6.3) не перпендикулярны к проекциям (tH; tv) на чертеже, если плоскость, в которой находится кривая – плоскость общего положения (см. рис. 6.1)
Рис. 6.3 – Проекция кривой b на эпюре
Монжа
На кривой можно выделить обыкновенные, особые и экстремальные точки.
Обыкновенная точка А кривой характеризуется тем, что направление движения точки по кривой и направление касательной остаются неизменными (см. рис. 6.2).
Если же в данной точке меняется направление касательной или направление самой кривой, точка является экстремальной или особой.
Рассмотрим некоторые из особых точек.
1.Точка перегиба E, в которой касательная и нормаль меняют направление, а кривая пересекает касательную (рис. 6.4а).
2.Вершина кривой B – точка, в которой нормаль является осью симметрии для некоторого участка кривой (рис. 6.4б).
3.Точки возврата O и C (клюв), в которых ветви кривой имеют общую касательную (рис. 6.4 в, г).
4.Двойная точка (F, F1), в которой кривая пересекает самое себя и меняется направление касательной (рис. 6.4 д, е).
studfiles.net
5.5. Развертки многогранников
Совмещение всех граней многогранника с одной плоскостью путем последовательного вращения их вокруг ребер называется разверткой многогранника.
Все грани многогранника на развертке изображаются в натуральной величине. Поэтому построение развертки сводится к построению натуральных величин граней многогранника. Их расположение и последовательность могут быть различны.
Чтобы получить развертку выпуклого многогранника нужно на его поверхности провести линию разреза, которая должна удовлетворять трем условиям:
1) проходить через все вершины выпуклого многогранника;
2) не должна быть замкнутой;
3) состоять из связанных между собой участков (линия разреза должна представлять собой одну линию).
Задача: Построить развертку прямой четырехугольной усеченной призмы, с основанием на плоскости Н, (рис. 5.10).
Решение.
1. Определяем линию разреза многогранника для построения развертки (САВD4312).
2. Устанавливаем, что нижнее основание (АВСD) призмы изображено в натуральную величину на горизонтальной плоскости проекций, а ребра призмы изображены в натуральную величину на фронтальной плоскости проекций.
3. Определяем натуральную величину верхнего основания (сечения) призмы методом вращения вокруг проецирующей оси проходящей через точку 1 перпендикулярно плоскости V: (1н,2н,3н,4н - натуральная величина сечения).

Рис. 5.10 – Построение развертки прямой четырехугольной
Усеченной призмы
4. Строим развертку призмы. На горизонтальной линии отложим отрезки DВ = DнВн; ВА = ВнАн; АС = АнСн; СD = СнDн (ширина каждой из боковых граней).
На перпендикулярах к этим отрезкам откладываются величины ребер D4=Dv4v; В2=Вv2v; А1=Аv1v; С3=СvЗv.
Многоугольник D42134D представляет собой развертку боковой поверхности призмы. Нижнее основание призмы, равное горизонтальной проекции его (АнВнDнСн) пристраивается, например, к стороне СD развертки боковой поверхности призмы. Натуральная величина основания (1н2’н3’н4’н) примыкает к развертке боковой поверхности стороной 24.
Глава 6. Кривые линии
6.1. Основные определения и проекции кривых
Кривая в начертательной геометрии определяется как множество последовательных положений точки, непрерывно перемещающейся в пространстве с изменением направления движения. Если движение точки изменяется по определенному закону, то кривая называется закономерной. Если движение произвольное, то получается кривая общего вида.
Кривые линии могут быть плоскими и пространственными. У плоской кривой все точки инцидентны некоторой плоскости. Закономерные плоские кривые могут определяться своими уравнениями - алгебраическими (окружность, гипербола, эллипс, парабола и др.) или трансцендентными (спираль Архимеда, синусоида). Кривые общего вида могут задаваться только графически. Степень уравнения алгебраической кривой определяет ее порядок. Графически порядок кривой определяется количеством точек пересечения с прямой, причем точки берутся как действительные, так и мнимые. Порядок кривой сохраняется и у проекций кривой. Если спроецировать кривую b на плоскость Н по направлению S, то на ней получится проекция кривой bH, обладающая всеми свойствами, которые сохраняются при параллельном проецировании (см. рис.6.1).

Рис. 6.1 – Проекция кривой Рис. 6.2 – Касательная к
b на плоскость Н кривой b
Касательной t к плоской кривой b в точке A называется предельное положение секущей t1, когда точки A1 и A2, оставаясь на кривой b, стремятся к точке A (рис.6.2).
Нормалью n к кривой b в точке A называют прямую инцидентную плоскости P и перпендикулярную к касательной t в этой точке. К плоской кривой может быть проведена только одна нормаль. К пространственной кривой в данной точке можно провести бесчисленное множество перпендикуляров к касательной, которые определяют нормальную плоскость.
Касательная к кривой в заданной точке проецируется в касательные к ее проекциям (tH; tv). Проекции нормали (nH; nV) (рис.6.3) не перпендикулярны к проекциям (tH; tv) на чертеже, если плоскость, в которой находится кривая – плоскость общего положения (см. рис. 6.1)
Рис. 6.3 – Проекция кривой b на эпюре
Монжа
На кривой можно выделить обыкновенные, особые и экстремальные точки.
Обыкновенная точка А кривой характеризуется тем, что направление движения точки по кривой и направление касательной остаются неизменными (см. рис. 6.2).
Если же в данной точке меняется направление касательной или направление самой кривой, точка является экстремальной или особой.
Рассмотрим некоторые из особых точек.
1.Точка перегиба E, в которой касательная и нормаль меняют направление, а кривая пересекает касательную (рис. 6.4а).
2.Вершина кривой B – точка, в которой нормаль является осью симметрии для некоторого участка кривой (рис. 6.4б).
3.Точки возврата O и C (клюв), в которых ветви кривой имеют общую касательную (рис. 6.4 в, г).
4.Двойная точка (F, F1), в которой кривая пересекает самое себя и меняется направление касательной (рис. 6.4 д, е).
studfiles.net