Оригами: как сделать додекаэдр из бумаги. Развертка пятиугольника

Развертка усеченной пирамиды. | МеханикИнфо

Правильная пятиугольная пирамида. Развертка усеченной пирамиды. 4.29/5 (85.71%) проголосовало 7

Правильная пирамида, в основании которой лежит правильный пятиугольник, усеченная плоскостью, показана на рис. 1.

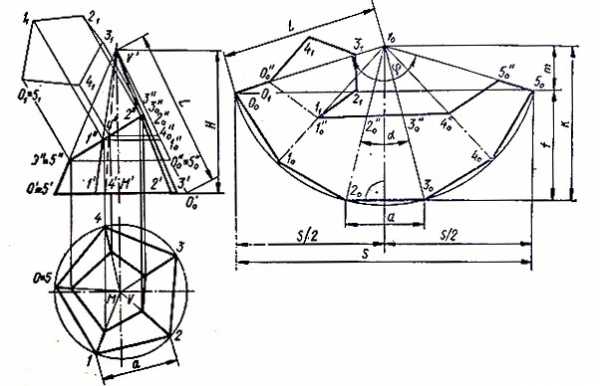
Рис. 1. Развертка правильного пятиугольника усеченного плоскостью.

Как построить сечение пятиугольной пирамиды?!

Через точки 3′, 3″ и 0′, 0″ проводятся прямые до пересечения в точке V’, являющейся вершиной пирамиды. Откладывается расстояние М’0′0 = М0. Точки 0’0 и V’ соединяются. Через точки пересечения ребер с плоскостью 0″, 1″, …, 5″ проводятся горизонтальные прямые до пересечения с прямой 0’0V’ в точках 0″0, 1″0, …, 5″0. Расстояние 0’0V’ = L определяет действительную длину ребра пирамиды.

Развертка строится следующим образом. Выбирается произвольный центр V0.

Из него радиусом, равным длине бокового ребра пирамиды R = L, описывается дуга. От произвольной точки 00 на дуге как хорда пять раз последовательно откладывается сторона основания а. Полученные точки 00, 10, …, 50 соединяются последовательно между собой и с вершиной V0. Из вершины откладываются расстояния V00″0 = V’0″0, V01″0 = V’1″0 и т. д. Полученные точки соединяются.

Для построения верхнего основания проводятся перпендикуляры к отрезку 0″3″ из точек 0″, 1″, 4″, 2″, 3″. После выбора произвольной точки 01 на перпендикуляре из точки 0″ из центра 01 радиусом 0″01″0 развертки описывается, дуга до пересечения с перпендикуляром в точке 11. Из центра 11 радиусом 1″02″0 описывается дуга до пересечения, перпендикуляра, проходящего через точку 2″, в точке 21. Построение продолжается при сохранении выбранного направления до замыкания многоугольника. Полученный многоугольник 011141 присоединяется к какому-либо из ребер развертки или выполняется отдельно.

mechanicinfo.ru

Построение пятиугольника подробно. - Чертежик

Построение пятиугольника рассмотрим подробно:

Чертим необходимую окружность;
Строим вспомогательную окружность такого же размера;
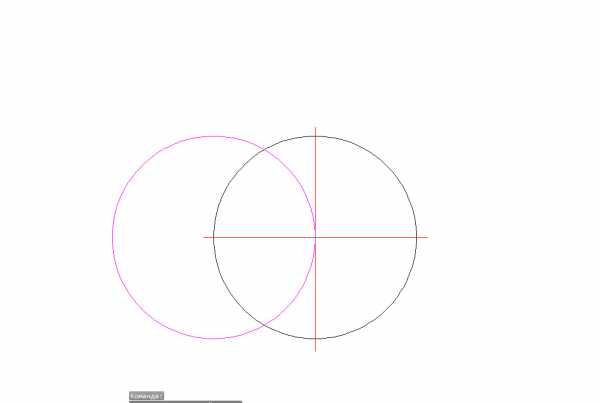
Соединяем точки пересечения прямой линией, полученные при построении вспомогательной окружности;
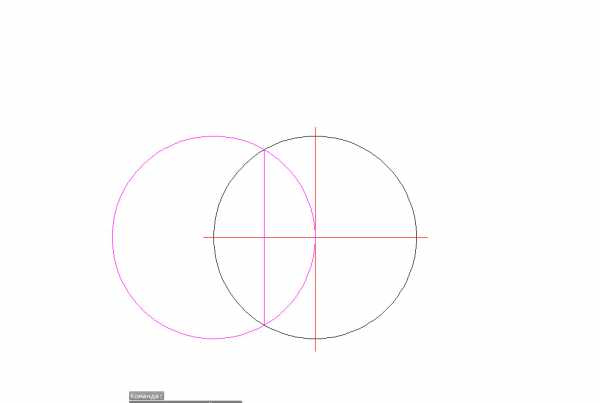
Соединяем пересечение прямой линии с осью первоначальной окружности;
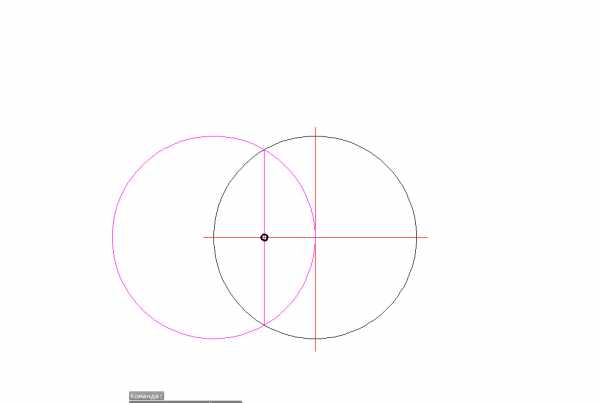
От полученной точки ведем отрезок к верхней точки пересечения окружности и оси;
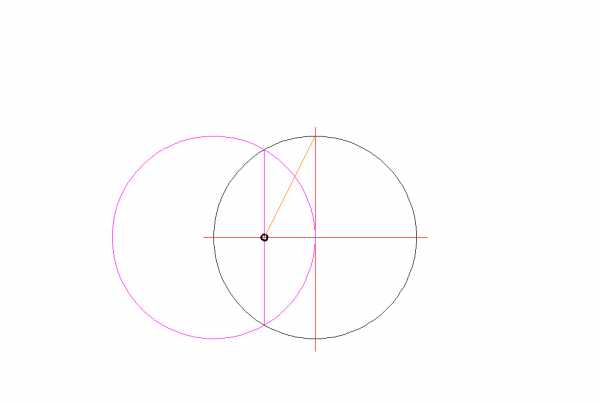
Полученный отрезок есть ни что иное как радиус 2-й вспомогательной окружности;
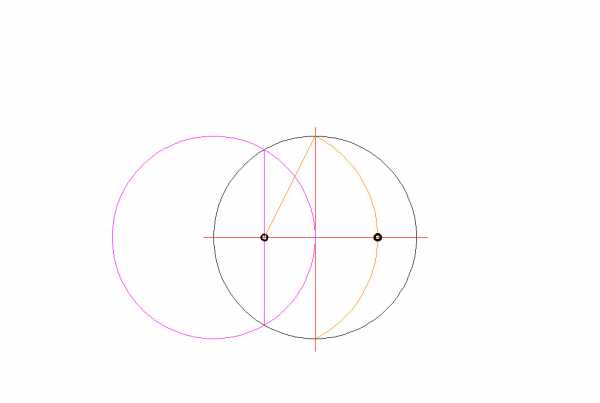
Соединяем прямой линией от верхней точки пересечения с осью к точки пересечения вспомогательной окружности с горизонтальной осью. Полученная прямая и есть необходимый нам радиус для построения пятиугольника;
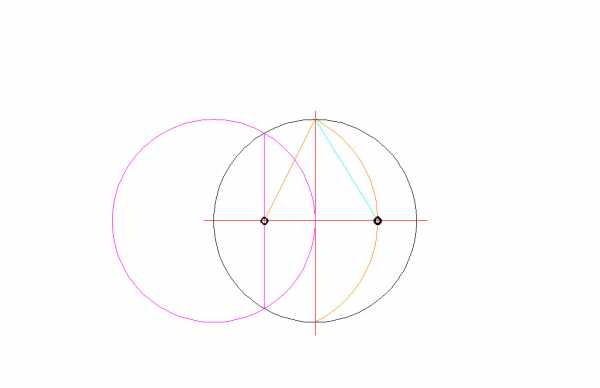
Строим «засечки» с первоначальной окружностью;
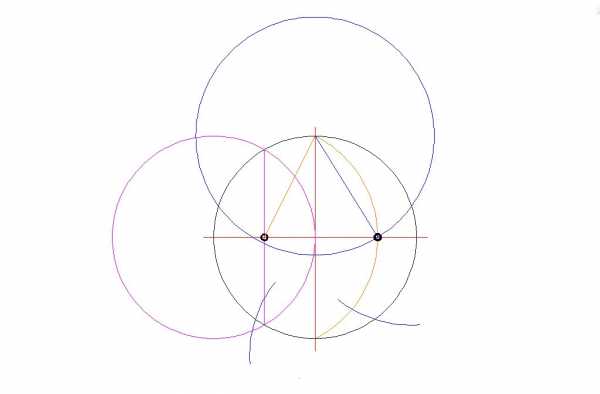
Соединяем полученные точки пересечения.

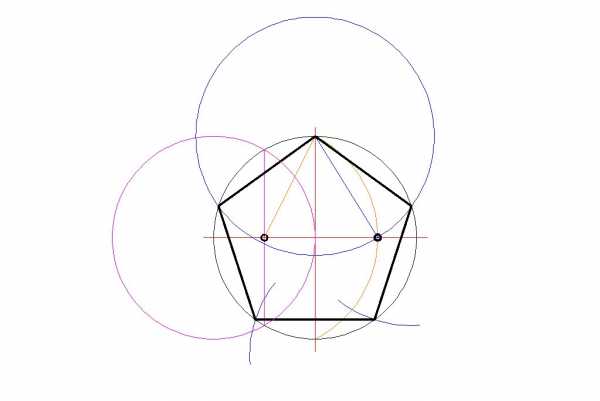
Вы можете посмотреть построение пятиугольника в видео:

Посмотрите примеры чертежей

chertegik.ru

Разузнай! - Додекаэдр - Как сделать правильный додекаэдр своими руками - Как сделать звездчатый додекаэдр

Додекаэдром называется правильный многогранник, составленный из двенадцати правильных пятиугольников. Эта эффектная объемная фигура обладает центром симметрии, называемым центром додекаэдра. Кроме того, в ней присутствуют пятнадцать плоскостей симметрии (в каждой грани любая из них проходит через середину противоположного ребра и вершину) и пятнадцать осей симметрии (пересекающих середины параллельных противолежащих ребер). Каждая из вершин додекаэдра является вершиной трех пятиугольников правильной формы.

Свое название конструкция получила по количеству входящих в нее граней (традиционно древние греки давали многогранникам имена, отображающие число граней, составляющих структуру фигуры). Таким образом, понятие «додекаэдр» образовано из значений двух слов: «додека» (двенадцать) и «хедра» (грань). Фигура относится к одному из пяти Платоновых тел (наряду с тетраэдром, октаэдром, гексаэдром (кубом) и икосаэдром). Интересно, что согласно многочисленным историческим документам, все они активно использовались жителями Древней Греции в виде настольных игральных костей и изготавливались из самого различного материала.

Правильные многогранники всегда привлекали людей своей красотой, органичностью и необыкновенным совершенством форм, но додекаэдр имеет особую историю, которая из года в год обрастает все новыми, иногда совершенно мистическими, фактами. Представители многих цивилизаций усматривали в нем сверхъестественную и таинственную сущность, утверждая, что: «Из числа двенадцать произрастает многое». На территориях древних разрушенных государств до сих пор находят маленькие фигурки в виде додекаэдров, выполненные из бронзы, камня или кости. Кроме того, при раскопках на землях современной Англии, Франции, Германии, Венгрии, Италии археологи обнаружили несколько сотен так называемых «римских додекаэдров», датирующихся II-III-м веками нашей эры. Основные размеры фигурок составляют от четырех до одиннадцати сантиметров, причем отличаются они самыми невероятными узорами, текстурами и техникой исполнения. Выдвинутая еще во времена Платона версия о том, что Вселенная представляет собой огромного размера додекаэдр, нашла подтверждение уже в начале XXI -го века. После тщательного анализа данных, полученных при помощи WMAP(многофункционального космического аппарата NASA), ученые согласились с предположением древнегреческих астрономов, математиков и физиков, в свое время занимавшихся вопросами изучения небесной сферы и ее строением. Более того, современные исследователи считают, что наша Вселенная представляет собой бесконечно повторяющийся набор додекаэдров.

Как сделать правильный додекаэдр своими руками

Сегодня конструкция данной фигуры нашла свое отображение во многих вариантах художественного творчества, архитектуре и строительстве. Народные умельцы изготавливают из цветной или белой бумаги необыкновенные по красоте оригами в виде ажурных додекаэдров, а из картона делают оригинальные и прочее). В продаже можно приобрести уже готовые наборы, содержащие все необходимое для изготовления сувениров, но наиболее интересно произвести весь процесс работы своими руками, начиная от построения отдельных деталей и заканчивая сборкой готовой конструкции.

Материалы:

Для того, чтобы сделать правильный додекаэдр из картона, необходим собственно сам материал и подручные средства:

ножницы,
карандаш,
ластик,
линейка,
клей.

Хорошо иметь тупой нож или какое-либо приспособление для загибания припусков, но если их нет, то вполне подойдет металлическая линейка или те же ножницы.

Делаем правильный додекаэдр

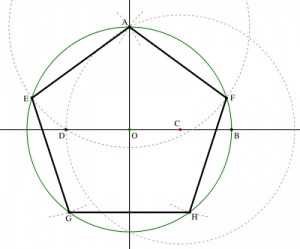
1. Самый первый этап в изготовлении – построение пятиугольника нужного размера. Должен получиться вот такой элемент. Он и станет основой фигуры.
Далее конструируете развертку додекаэдра с учетом припусков на склеивание. В результате получится «выкройка» приблизительно такого вида. Варианты могут различаться, если припуски будут другой формы или размещены на других гранях.
Аккуратно по линиям сгибаете припуски.
Склеиваете.
Наносите на готовый додекаэдр нужный рисунок или декорируете другим выбранным способом.

Готово!

Как сделать звездчатый додекаэдр

Звездчатые додекаэдры имеют более сложную конструкцию по сравнению с обычными. Эти многогранники подразделяются на малый (первого продолжения), средний (второго продолжения) и большой (последняя звездчатая форма правильного додекаэдра). Каждый из них отличается своими особенностями построения и сборкой. Для работы Вам потребуются те же материалы и инструменты, что и для изготовления стандартного додекаэдра. Если Вы решили сделать первый вариант (малый додекаэдр), то необходимо построить чертеж первого элемента, который станет основой для всей конструкции (в дальнейшем производится ее склеивание или сборка деталей при помощи скрепок).

Делаем звездчатый додекаэдр

Строите схему основной детали нужных размеров с необходимыми припусками. Должен получиться приблизительно такой элемент.
По обозначенным линиям сгибаете, в том числе не забываете о припусках.

Склеиваете каждую деталь по отдельности.
Собираете додекаэдр полностью.
Раскрашиваете или наносите любое из выбранных изображений.

Готово!

Видео как сделать Додекаэдр:

Представляем Вам некоторые видео как сделать додекаэдр:

И парочку тяжелых, для трудолюбивых..

Вперед!

Усечённые правильные пирамиды - Mnogogranniki.ru

Готовый набор "Волшебные грани"

Для сборки многогранников мы можем вам предложить уже готовые развёртки - вырезанные и подогнутые.

Для этого вам нужно воспользоваться деталями набора Волшебные грани № 14.

Кроме того, в самом выпуске вы найдете информацию о строении многогранников.

Сборка правильной четырехугольной пирамиды:

Вращение готового многогранника, собранного из этих деталей:

Сборка правильной четырехугольной пирамиды:

Вращение готового многогранника (усечённой четырехугольной пирамиды), собранного из этих деталей:

Сборка пирамиды со звёздчатым основанием:

Вращение готового многогранника, собранного из этих деталей:

Сборка би-пирамиды с основанием в форме пятиконечной звезды:

Вращение готового многогранника, собранного из этих деталей:

mnogogranniki.ru

как сделать додекаэдр из бумаги

Додекаэдр - это многогранник, состоящий из 12 одинаковых пятиугольников. Это базовая фигура для множества поделок: от настольных календарей до ажурных подвесных фонариков.

Как сделать додекаэдр из бумаги?

Можно построить пятиугольник самостоятельно - это несложно и гарантирует высокую точность рисунка. Для построения правильного пятиугольника понадобится циркуль и линейка. Нарисуйте круг необходимого размера. Проведите в любом месте радиус. К нему перпендикулярно проведите другой радиус. Затем один из радиусов разделите на две равные части. Каждая половинка будет радиусом другой, маленькой окружности, которая выполнит роль вспомогательной. Затем соедините центр этой вспомогательной окружности с тем местом, где основную окружность пересекает другой радиус (допустим, в точке А). Полученная линия пересечет вспомогательную окружность в определенной точке - В. Расстояние АВ и есть одна десятая часть окружности. Именно это расстояние циркулем отметьте на основной окружности, а затем соедините прямыми линиями эти точки через одну - правильный пятиугольник готов!

Есть и другие методы. Например, пятиугольник можно построить с помощью транспортира, но точности он не гарантирует. Наиболее легий способ - взять готовую схему, распечатать ее и по этой "выкройке" уже мастерить из подходящей бумаги поделку. Но этот способ, несмотря на простоту, подходит не всегда - ведь иногда нужно сделать додекаэдр какого-то конкретного размера. Можно увеличить один пятиугольник до нужного масштаба и распечатать только его, затем построить фигуру по схеме ниже.

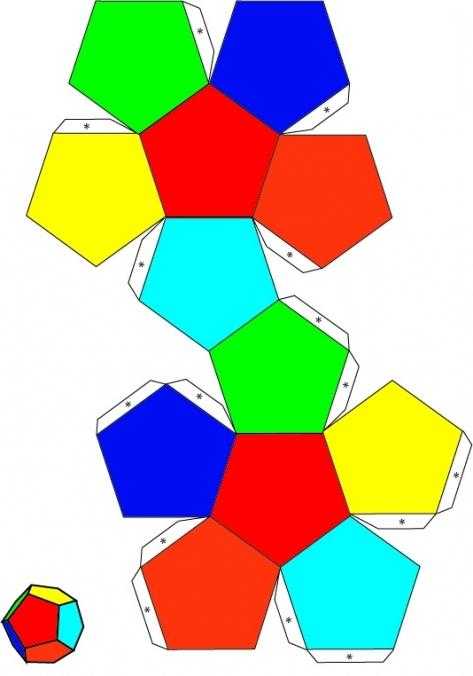
Но "выкройка" - это еще не готовая поделка. Как сделать додекаэдр из бумаги? Для этого понадобятся:

1. Бумага, подходящая по плотности. Она не должна быть слишком тонкой или же слишком толстой - желательно 220 г/м², именно такой плотностью обладает картон, который продают в детских наборах. Хотя из толстого картона вполне можно создавать объемные фигуры, нужно только предварительно обработать все сгибы - слегка надрезать или хорошо продавить, чтобы они хорошо и ровно сгибались.

2. Ножницы, карандаш, клей, вязальная спица или канцелярский нож

Советы по изготовлению додекаэдра

Бумагу в местах сгибов желательно слегка продавить спицей, тупой стороной канцелярского ножа или чем-то острым, но не режущим. Аккуратные ровные сгибы - половина успеха.

Если клея под рукой нет, додекаэдр можно собрать, как конструктор, сделав надрезы по сгибам, а затем просто вставив стороны одна в другую.

Если вы собираете додекаэдр в модульной технике (инструкция ниже), то места соединений желательно проклеивать или закреплять скрепками, поскольку конструкция станет устойчивой только после закрепления последнего модуля.

Додекаэдр в технике оригами

Модуль оригами - отличная основа для додекаэдра. Как сделать додекаэдр из бумаги в модульной технике? Понадобится 30 прямоугольных или квадратных листов бумаги. Каждый из листочков складывается пополам, затем каждую половинку нужно отогнуть в противоположную сторону - получится "гармошка" в четыре сложения. Иногда, если лист не квадратный, делают "гармошку" в три сложения. В итоге у вас в руках узкая промоугольная полоска. Затем с каждой стороны прямоугольника по узкой стороне нужно отогнуть уголок. Уголки складываются в одну сторону - это будущие крепления, которые будут заправляться в "гармошку". Затем согните модуль вовнутрь наискосок по диагонали от маленьких боковых уголков. Таким образом, один модуль для оригами додекаэдра - трехмерный, он включает два ребра будущей фигуры и уголки. Когда все модули готовы, можно начинать сборку.

Сборка начинается с одного узла, для которого необходимо взять три модуля. На рисунке ниже это голубой, розовый и желтый модули оригами. Схемы сборки достаточно просты, и с такими фигурами легко справляются даже начинающие.

Какие поделки можно сделать на основе додекаэдра?

Каждая сторона додекаэдра из бумаги - это плоский пятиугольник, который сам по себе может являться основой для самых разных и причудливых форм. Например, на фото ниже пятиугольник заменен пятиконечнй звездой. Ребра в такой фигуре отсутствуют, хотя предполагаются. Как сделать додекаэдр из бумаги в виде звезды? Замените в развертке, представленной выше, каждый пятиугольник необходимой пятиконечной фигурой и соедините их не по ребрам, а по вершинам.

На этом фото представлен звездчатый додекаэдр. В основе каждого "луча" лежит все тот же пятиугольник.

Вместо пятиугольных пирамид может быть выполнена любая объемная фигура.

На фото ниже в качестве пятиугольников выступают более сложные модули оригами, схемы которых заинтересовавшиеся этой техникой смогут найти в специальной литературе.

В любом случае освоение даже простейшей схемы сборки додекаэдра уже даст огромные возможности для творчества и поиска своих собственных вариантов.

fb.ru

Правильные пирамиды - Mnogogranniki.ru - создание моделей многогранников из бумаги

Готовый набор "Волшебные грани"

Для сборки многогранников мы можем вам предложить уже готовые развёртки - вырезанные и подогнутые.

Для этого вам нужно воспользоваться деталями набора Волшебные грани № 14.

Кроме того, в самом выпуске вы найдете информацию о строении многогранников.

Сборка правильной четырехугольной пирамиды:

Вращение готового многогранника, собранного из этих деталей:

Сборка усечённой четырехугольной пирамиды:

Вращение готового многогранника, собранного из этих деталей:

Сборка пирамиды со звёздчатым основанием:

Вращение готового многогранника, собранного из этих деталей:

Сборка би-пирамиды с основанием в форме пятиконечной звезды:

Вращение готового многогранника, собранного из этих деталей:

mnogogranniki.ru

Пирамида

Пирамидой называется многогранник, у которого одна из граней - основание - какой - нибудь многоугольник, а все остальные - боковые - треугольники, имеющие общую вершину. Общая вершина S боковых граней называется вершиной пирамиды, а перпендикуляр SO, опущенный из вершины на плоскость основания, - высотой ее (фиг.286,а).

Пирамиды бывают: треугольные, четырехугольные и т. д., смотря по тому, что является основанием - треугольник, четырехугольник и т. д. Пирамида называется правильной (фиг.286,б), если, во - первых, ее основанием является правильный многоугольник, и, во - вторых, высота проходит через центр этого многоугольника. В противном случае пирамида называется неправильной (фиг.286,в). В правильной пирамиде все боковые ребра равны между собой (как наклонные с равными проекциями). Поэтому все боковые грани правильной пирамиды есть равные равнобедренные треугольники.Анализ элементов правильной шестиугольной пирамиды и их изображение на комплексном чертеже (фиг.287).

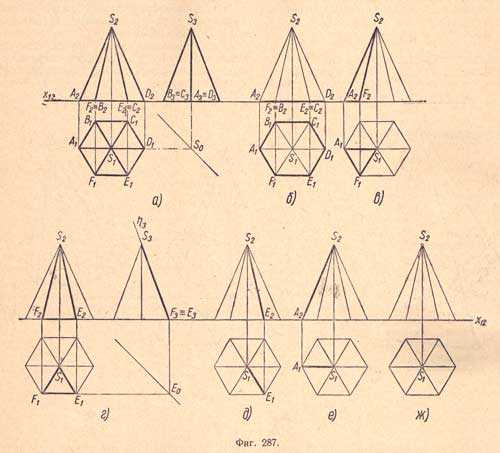
а) Комплексный чертеж правильной шестиугольной пирамиды. Основание пирамиды расположено на плоскости П1; две стороны основания пирамиды параллельны плоскости проекций П2.б) Основание ABCDEF - шестиугольник, расположенный в плоскости проекций П1.в) Боковая грань ASF - треугольник, расположенный в плоскости общего положения.г) Боковая грань FSE - треугольник, расположенный в профильно - проектирующей плоскости .д) Ребро SE - отрезок общего положения.е) Ребро SA - фронтальный отрезок.ж) Вершина S пирамиды - точка в пространстве. На (фиг.288 и фиг.289) приведены примеры последовательных графических операций при выполнении комплексного чертежа и наглядных изображений (аксонометрии) пирамид.Изображение правильной пятиугольной пирамиды.

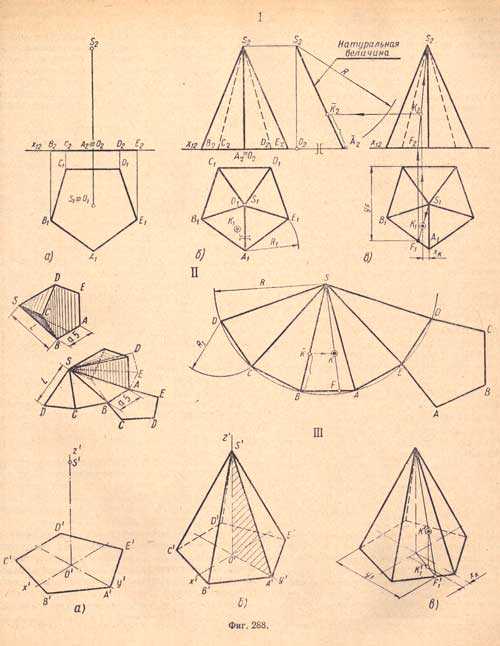
Дано: 1. Основание расположено на плоскости П1. 2. Одна из сторон основания параллельна оси х12.I. Комплексный чертеж.I, а. Проектируем основание пирамиды - многоугольник, по данному условию лежащий в плоскости П1. Проектируем вершину - точку, расположенную в пространстве. Высота точки S равна высоте пирамиды. Горизонтальная проекция S1 точки S будет в центре проекции основания пирамиды (по условию).I, б. Проектируем ребра пирамиды - отрезки; для этого соединяем прямыми проекции вершин основания ABCDE с соответствующими проекциями вершины пирамиды S. Фронтальные проекции S2 С2и S2 D2 ребер пирамиды изображаем штриховыми линиями, как невидимые, закрытые гранями пирамиды (SBА и SAE).I, в. Дана горизонтальная проекция К1 точки К на боковой грани SBА, требуется найти ее фронтальную проекцию. Для этого проводим через точки S1и K1 вспомогательную прямую S1F1, находим ее фронтальную проекцию и на ней при помощи вертикальной линии связи определяем место искомой фронтальной проекции K2 точки К.II. Развертка поверхности пирамиды - плоская фигура, состоящая из боковых граней - одинаковых равнобедренных треугольников одна сторона которых равна стороне основания, а две другие - боковым ребрам, и из правильного многоугольника - основания. Натуральные размеры сторон основания выявлены на его горизонтальной проекции. Натуральные размеры ребер на проекциях не выявлены. Гипотенуза S2¯A2 (фиг.288, 1, б) прямоугольного треугольника S2O2¯A2, у которого большой катет равен высоте S2O2 пирамиды, а малый - горизонтальной проекции ребра S1A1является натуральной величиной ребра пирамиды. Построение развертки следует выполнять в следующем порядке:а) из произвольной точки S (вершины) проводим дугу радиусом R, равным ребру пирамиды;б) на проведенной дуге отложим пять хорд размером R1 равным стороне основания;в) соединим прямыми точки D, С, В, А, Е, D последовательно между собой и с точкой S, получим пять равнобедренных равных треугольников, составляющих развертку боковой поверхности данной пирамиды, разрезанной по ребру SD;г) пристраиваем к любой грани основание пирамиды - пятиугольник, пользуясь способом триангуляции, например к грани DSE. Перенос на развертку точки К осуществляется вспомогательной прямой с помощью размера В1F1, взятого на горизонтальной проекции, и размера А2К2, взятого на натуральной величине ребра.III. Наглядное изображение пирамиды в изометрии.III, а. Изображаем основание пирамиды, пользуясь координатами согласно (фиг.288, 1, а). Изображаем вершину пирамиды, пользуясь координатами по (фиг.288, 1, а).III, б. Изображаем боковые ребра пирамиды, соединяя вершину с вершинами основания. Ребро S'D' и стороны основания C'D' и D'E' изображаем штриховыми линиями, как невидимые, закрытые гранями пирамиды C'S'B', B'S'A' и A'S'E'.III, e. Определяем на поверхности пирамиды точку К, пользуясь размерами уF и хK. Для ди-метрического изображения пирамиды следует придерживаться той же последовательности.Изображение неправильной треугольной пирамиды.

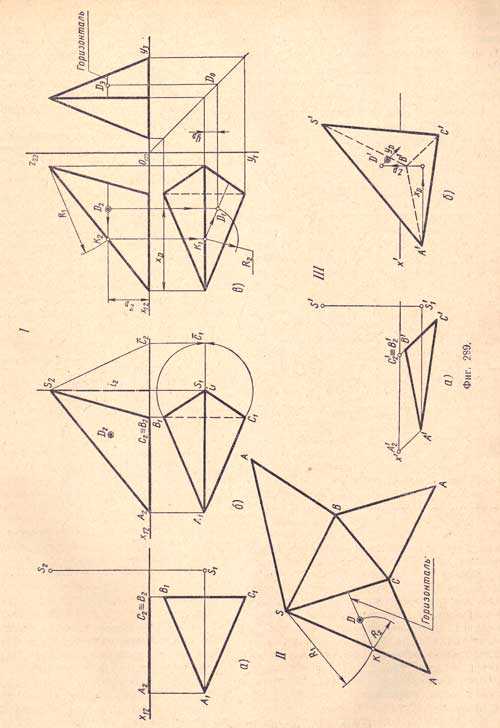
Дано: 1. Основание расположено на плоскости П1.2. Сторона ВС основания перпендикулярна оси X.I. Комплексный чертежI, а. Проектируем основание пирамиды - равнобедренный треугольник, лежащий в плоскости П1, и вершину S - точку, расположенную в пространстве, высота которой равна высоте пирамиды.I, б. Проектируем ребра пирамиды - отрезки, для чего соединяем прямыми одноименные проекции вершин основания с одноименными проекциями вершины пирамиды. Горизонтальную проекцию стороны основания ВС изображаем штриховой линией, как невидимую, закрытую двумя гранями пирамиды ABS, ACS.I, в. На фронтальной проекции A2С2S2 боковой грани дана проекция D2 точки D. Требуется найти ее горизонтальную проекцию. Для этого через точку D2 проводим вспомогательную прямую параллельно оси х12 - фронтальную проекцию горизонтали, затем находим ее горизонтальную проекцию и на ней, при помощи вертикальной линии связи, определяем место искомой горизонтальной проекции D1 точки D.II. Построение развертки пирамиды. Натуральные размеры сторон основания выявлены на горизонтальной проекции. Натуральная величина ребра AS выявлена на фронтальной проекции; натуральной величины ребер BS и CS в проекциях нет, величину этих ребер выявляем путем вращения их вокруг оси i, перпендикулярной к плоскости П1 проходящей через вершину пирамиды S. Новая фронтальная проекция ¯C2S2 является натуральной величиной ребра CS. Последовательность построения развертки поверхности пирамиды:а) вычерчиваем равнобедренный треугольник - грань CSB, основание которого равно стороне основания пирамиды СВ, а боковые стороны - натуральной величине ребра SC;б) к сторонам SC и SB построенного треугольника пристраиваем два треугольника - грани пирамиды CSA и BSA, а к основанию СВ построенного треугольника - основание СВА пирамиды, в результате получаем полную развертку поверхности данной пирамиды. Перенос на развертку точки D выполняется в следующем порядке: сначала на развертке боковой грани ASC проводим линию горизонтали при помощи размера R1 а затем определяем на линии горизонтали место точки D при помощи размера R2.III. Наглядное изображение пирамиды е фронтальной диметрической проекцииIII, а. Изображаем основание А'В'С и вершину S' пирамиды, пользуясь координатами согласно (фиг.289, 1, а).

III, б. Изображаем ребра S'A, S'C' и S'B' пирамиды, соединяя вершину S' с вершинами основания А'В'С'. Ребро S'B' и стороны основания A'В' и В'С' изображаем штриховыми линиями, как невидимые, закрытые гранью A'S'C'. Для определения на поверхности пирамиды места точки D пользуемся координатами точки xD, yD, zD (фиг.289, 1, в), причем координата yD сокращается вдвое.

Вращения и развертки поверхностей.....