Содержание
Удельное сопротивление (при 20° C)
| Вещество | Уровень удельного сопротивления, мкОм • мм2/м |
|---|---|
| Алюминий | 0,028 |
| Вольфрам | 0,055 |
| Железо | 0,098 |
| Золото | 0,023 |
| Константан | 0,44−0,52 |
| Латунь | 0,025−0,06 |
| Манганин | 0,42−0,48 |
| Медь | 0,0175 |
| Молибден | 0,057 |
| Никелин | 0,39−0,45 |
| Никель | 0,100 |
| Олово | 0,115 |
| Ртуть | 0,958 |
| Свинец | 0,221 |
| Серебро | 0,016 |
| Тантал | 0,155 |
| Фехраль | 1,1−1,3 |
| Хром | 0,027 |
| Цинк | 0,059 |
| Вещество | К | Вещество | К |
|---|---|---|---|
| Алюминий | 0,0042 | Олово | 0,0042 |
| Вольфрам | 0,0048 | Платина | 0,004 |
| Константан | 0,2 | Ртуть | 0,0009 |
| Латунь | 0,001 | Свинец | 0,004 |
| Медь | 0,0043 | Серебро | 0,0036 |
| Манганин | 0,3 | Сталь | 0,006 |
| Молибден | 0,0033 | Тантал | 0,0031 |
| Никель | 0,005 | Хром | 0,006 |
| Никелин | 0,0001 | Фехраль | 0,0002 |
| Нихром | 0,0001 | Цинк | 0,004 |
Сплавы сопротивления
- Константан (58,8 Cu, 40 Ni, 1,2 Mn)
- Манганин (85 Cu, 12 Mn, 3 Ni)
- Нейзильбер (65 Cu, 20 Zn, 15 Ni)
- Никелин (54 Cu, 20 Zn, 26 Ni)
- Нихром (67,5 Ni, 15 Cr, 16 Fe, 1,5 Mn)
- Реонат (84Cu, 12Mn, 4 Zn)
- Фехраль (80 Fe, 14 Cr, 6 Al)
Удельное сопротивление нихрома
Рассмотрим электронную теорию данного явления. При движении по проводнику свободные электроны постоянно встречают на своем пути другие электроны и атомы. Взаимодействуя с ними, свободный электрон теряет часть своего заряда. Таким образом, электроны сталкиваются с сопротивлением со стороны материала проводника. Каждое тело имеет свою атомную структуру, которая оказывает электрическому току разное сопротивление. Единицей сопротивления принято считать Ом.
При движении по проводнику свободные электроны постоянно встречают на своем пути другие электроны и атомы. Взаимодействуя с ними, свободный электрон теряет часть своего заряда. Таким образом, электроны сталкиваются с сопротивлением со стороны материала проводника. Каждое тело имеет свою атомную структуру, которая оказывает электрическому току разное сопротивление. Единицей сопротивления принято считать Ом.
Сопротивление каждого отдельно взятого проводника (обозначается R или r.) зависит от свойств материала, из которого он изготовлен. Для точной характеристики электрического сопротивления того или иного материала было введено понятие — удельное сопротивление (нихрома, алюминия и т. д.). Удельным считается сопротивление проводника длиной до 1 м, сечение которого — 1 кв. мм. Этот показатель обозначается буквой p. Каждый материал, использующийся в производстве проводника, обладает своим удельным сопротивлением. Для примера рассмотрим удельное сопротивление нихрома и фехрали.
- Х15Н60 — 1.
 13 Ом* мм2/м
13 Ом* мм2/м - Х23Ю5Т — 1.39 Ом* мм2/м
- Х20Н80 — 1.12 Ом* мм2/м
- ХН70Ю — 1.30 Ом* мм2/м
- ХН20ЮС — 1.02 Ом* мм2/м
Применение
Высокий уровень удельное сопротивления нихрома, фехрали позволяет использовать эти материалы в произвгоодстве нагревательных элементов. Самая распространенная продукция — нихромовая нить, лента, полоса Х15Н60 и Х20Н80, а также фехралевая проволока Х23Ю5Т. для приборов теплового действия, бытовых приборов и электронагревательных элементов промышленных печей.
Удельное сопротивление и сверхпроводимость
Публикации по материалам Д. Джанколи. «Физика в двух томах» 1984 г. Том 2.
На опыте установлено, что сопротивление R металлического проводника прямо пропорционально его длине L и обратно пропорционально площади его поперечного сечения А:
R = ?L/А (26. 4)
4)
где коэффициент ? называется удельным сопротивлением и служит характеристикой вещества, из которого изготовлен проводник. Это соответствует здравому смыслу: сопротивление толстого провода должно быть меньше, чем тонкого, поскольку в толстом проводе электроны могут перемещаться по большей площади. И можно ожидать роста сопротивления с увеличением длины проводника, так как увеличивается количество препятствий на пути потока электронов.
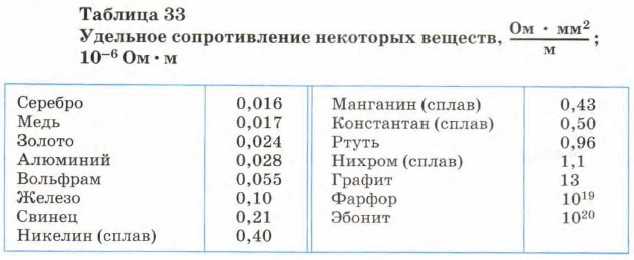
Типичные значения ? для разных материалов приведены в первом столбце табл. 26.2. (Реальные значения зависят от чистоты вещества, термической обработки, температуры и других факторов.)
|
Таблица 26.2. Удельное сопротивление и температурный коэффициент сопротивления (ТКС) (при 20 °С) | ||
| Вещество | Удельное сопротивление ?,Ом·м | ТКС ?,°C-1 |
| Проводники | ||
| Серебро | 1,59·10-8 | 0,0061 |
| Медь | 1,68·10-8 | 0,0068 |
| Алюминий | 2,65·10-8 | 0,00429 |
| Вольфрам | 5,6·10-8 | 0,0045 |
| Железо | 9,71·10-8 | 0,00651 |
| Платина | 10,6·10-8 | 0,003927 |
| Ртуть | 98·10-8 | 0,0009 |
| Нихром (сплав Ni, Fe, Сг) | 100·10-8 | 0,0004 |
| Полупроводники 1) | ||
| Углерод (графит) | (3-60)·10-5 | -0,0005 |
| Германий | (1-500)·10-5 | -0,05 |
| Кремний | 0,1 — 60 | -0,07 |
| Диэлектрики | ||
| Стекло | 109 — 1012 | |
| Резина твердая | 1013 — 1015 | |
1) Реальные значения сильно зависят от наличия даже малого количества примесей. | ||
Самым низким удельным сопротивлением обладает серебро, которое оказывается, таким образом, наилучшим проводником; однако оно дорого. Немногим уступает серебру медь; ясно, почему провода чаще всего изготовляют из меди.
Удельное сопротивление алюминия выше, чем у меди, однако он имеет гораздо меньшую плотность, и в некоторых случаях ему отдают предпочтение (например, в линиях электропередач), поскольку сопротивление проводов из алюминия той же массы оказывается меньше, чем у медных. Часто пользуются величиной, обратной удельному сопротивлению:
? = 1/? (26.5)
? называемой удельной проводимостью. Удельная проводимость измеряется в единицах (Ом·м) -1.
Удельное сопротивление вещества зависит от температуры. Как правило, сопротивление металлов возрастает с температурой. Этому не следует удивляться: с повышением температуры атомы движутся быстрее, их расположение становится менее упорядоченным, и можно ожидать, что они будут сильнее мешать движению потока электронов. В узких диапазонах изменения температуры удельное сопротивление металла увеличивается с температурой практически линейно:
В узких диапазонах изменения температуры удельное сопротивление металла увеличивается с температурой практически линейно:
где ?T — удельное сопротивление при температуре Т, ?0 — удельное сопротивление при стандартной температуре Т0, а ? — температурный коэффициент сопротивления (ТКС). Значения а приведены в табл. 26.2. Заметим, что у полупроводников ТКС может быть отрицательным. Это очевидно, поскольку с ростом температуры увеличивается число свободных электронов и они улучшают проводящие свойства вещества. Таким образом, сопротивление полупроводника с повышением температуры может уменьшаться (хотя и не всегда).
Значения а зависят от температуры, поэтому следует обращать внимание на диапазон температур, в пределах которого справедливо данное значение (например, по справочнику физических величин). Если диапазон изменения температуры окажется широким, то линейность будет нарушаться, и вместо (26.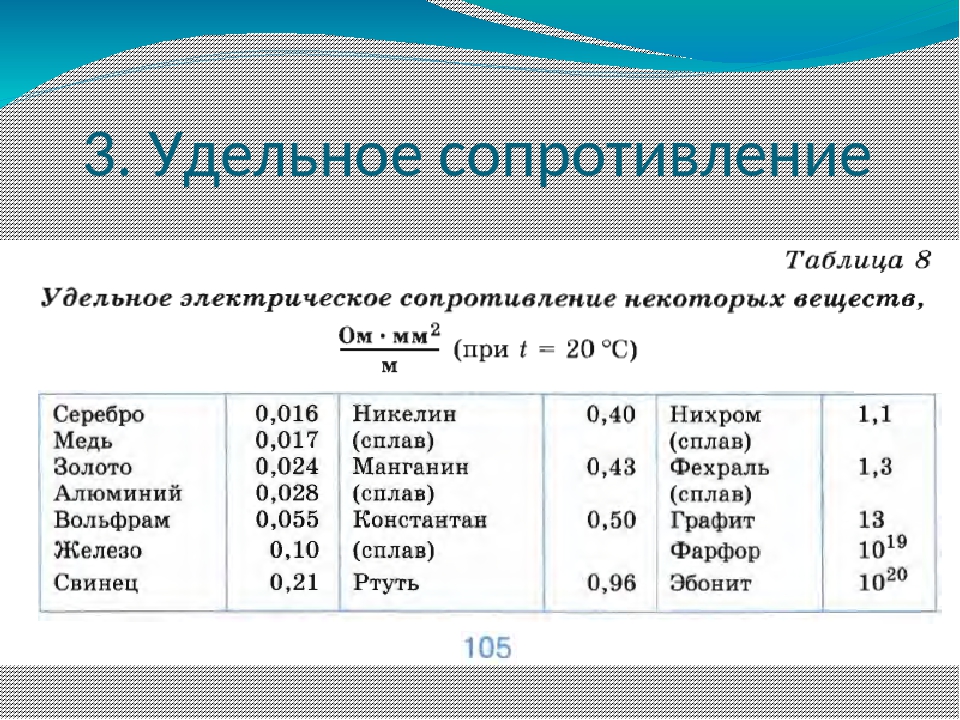 6) надо использовать выражение, содержащее члены, которые зависят от второй и третьей степеней температуры:
6) надо использовать выражение, содержащее члены, которые зависят от второй и третьей степеней температуры:
?T = ?0(1+?Т+ + ?Т 2 + ?Т 3),
где коэффициенты ? и ? обычно очень малы (мы положили Т0 = 0°С), но при больших Т вклад этих членов становится существенным.
При очень низких температурах удельное сопротивление некоторых металлов, а также сплавов и соединений падает в пределах точности современных измерений до нуля. Это свойство называют сверхпроводимостью; впервые его наблюдал нидерландский физик Гейке Камер-линг-Оннес (1853-1926) в 1911 г. при охлаждении ртути ниже 4,2 К. При этой температуре электрическое сопротивление ртути внезапно падало до нуля.
Сверхпроводники переходят в сверхпроводящее состояние ниже температуры перехода, составляющей обычно несколько градусов Кельвина (чуть выше абсолютного нуля). Наблюдался электрический ток в сверхпроводящем кольце, который практически не ослабевал в отсутствие напряжения в течение нескольких лет.
В последние годы сверхпроводимость интенсивно исследуется с целью выяснить ее механизм и найти материалы, обладающие сверхпроводимостью при более высоких температурах, чтобы уменьшить стоимость и неудобства, обусловленные необходимостью охлаждения до очень низких температур. Первую успешную теорию сверхпроводимости создали Бардин, Купер и Шриффер в 1957 г. Сверхпроводники уже используются в больших магнитах, где магнитное поле создается электрическим током (см. гл. 28), что значительно снижает расход электроэнергии. Разумеется, для поддержания сверхпроводника при низкой температуре тоже затрачивается энергия.
Продолжение следует: Мощность.
Альтернативные статьи: Электрический ток, Закон Ома.
Замечания и предложения принимаются и приветствуются!
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Физика твердого тела — Почему серебро с большим количеством свободных электронов имеет меньшее сопротивление?
$\begingroup$
В моей книге (Краткая физика ICSE) упоминаются следующие сведения о зависимости сопротивления от материала проводника: —
Зависимость от материала проводника: Различные материалы имеют
различная концентрация свободных электронов и, следовательно, сопротивление
проводника зависит от его материала.Металлы, такие как серебро,
медь, алюминий, свинец и др. имеют концентрацию свободных
электронов в порядке убывания, поэтому их одинаковые провода предлагают
сопротивление в порядке возрастания .
Я сомневаюсь в следующем Заявлении:
Металлы, такие как серебро, медь, алюминий, свинец и т. д., имеют концентрацию свободного
электронов в порядке убывания, поэтому их одинаковые провода предлагают
сопротивление в порядке возрастания
Это означает, что, поскольку серебро имеет большое количество свободных электронов, оно обеспечивает низкое сопротивление. У меня возникают сомнения, что, поскольку серебро имеет большее количество свободных электронов, количество столкновений электронов с положительными ионами серебра также будет больше, что должно привести к более высокое сопротивление (поскольку большее количество свободных электронов означает большее количество столкновений), но происходит обратное (т. е. серебро предлагает более низкое, чем более высокое сопротивление). Итак, мой первый вопрос: почему серебро с большим количеством свободных электронов имеет низкое сопротивление?
Итак, мой первый вопрос: почему серебро с большим количеством свободных электронов имеет низкое сопротивление?
Точно так же, как свинец с меньшим количеством свободных электронов имеет более высокое сопротивление?
- физика твердого тела
- электроны
- электрическое сопротивление
- проводники
- металлы
$\endgroup$
1
$\begingroup$
Количество электронов влияет на скорость рассеяния, но для этих металлов это несущественно. Скорее, в их рассеянии обычно преобладают фононы, а при более низких температурах — дефекты. Таким образом, в первом приближении скорость рассеяния можно считать фиксированной. Тогда проводимость (то есть обратное удельное сопротивление) пропорциональна числу электронов.
Ваша книга немного обманчива, поскольку удельное сопротивление этих металлов пропорционально скорости рассеяния, а кто сказал, что скорость у них одинакова? На самом деле скорости рассеяния немного отличаются, и различия между сопротивлениями не могут быть полностью объяснены числом электронов.
 13 Ом* мм2/м
13 Ом* мм2/м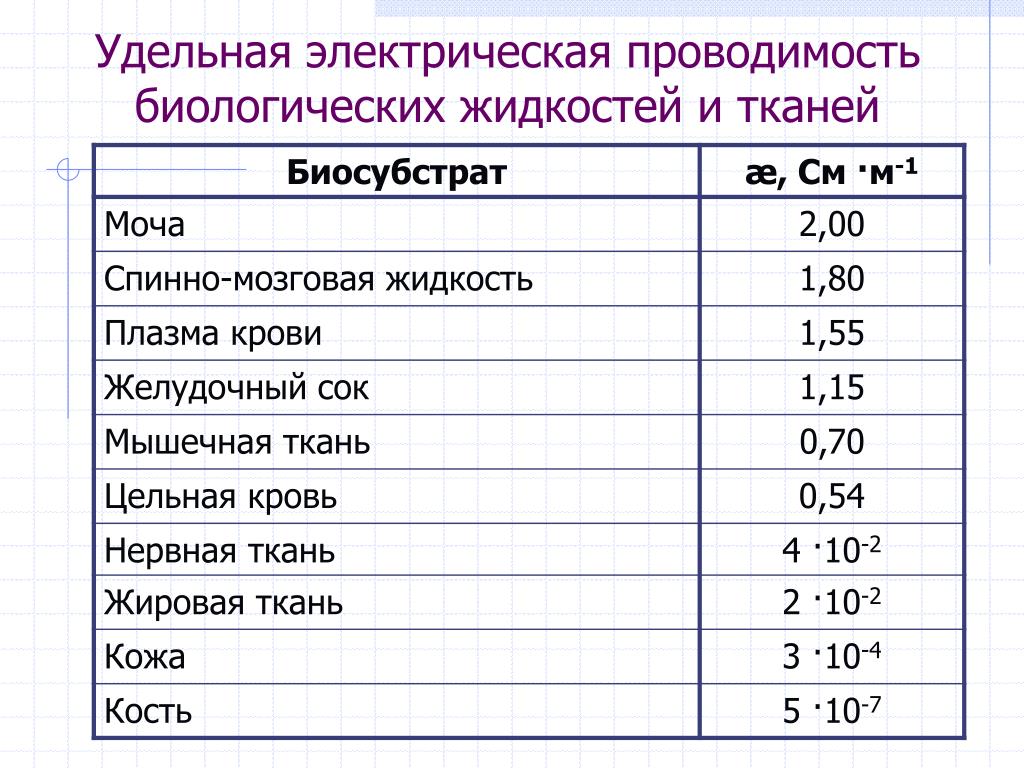 Удельное сопротивление выражается в единицах, которые являются произведением
Удельное сопротивление выражается в единицах, которые являются произведением
 1
1 1
1
 Всемирная паутина (Интернет) была в значительной степени неизвестной сущностью в то время.
Всемирная паутина (Интернет) была в значительной степени неизвестной сущностью в то время. Металлы, такие как серебро,
Металлы, такие как серебро,