Радиус и высота конуса. Как вычислить угол конуса

Нормальные конусности и углы

Источник: ГОСТ 8593-81

Конусность К есть отношение разности диаметров двух поперечных сечений конуса к расстоянию между ними.

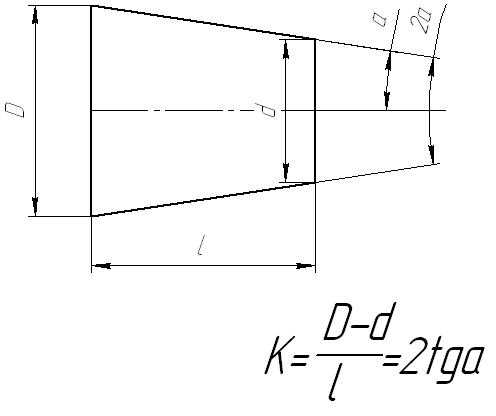
Уклон "i" есть отношение разности размеров двух поперечных сечений к расстоянию между ними.

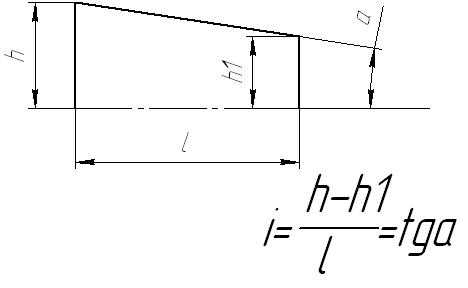
Таблица 1. Углы конусности

Конусность К	Угол конуса 2а	Угол уклона а	Исходное значение (К или 2а)
1:200	0°7'11"	0°8'36"	1:200
1:100	0°34'23"	0°17'11"	1:100
1:50	1°8'46"	0°34'23"	1:50
1:30	1°54'35"	0°57'17"	1:30
1:20	2°51'51"	1°25'56"	1:20
1:15	3°49'6"	1°54'33"	1:15
1:12	4°46'19"	2°23'9"	1:12
1:10	5°43'29"	2°51'45"	1:10
1:8	7°9'10"	3°34'35"	1:8
1:7	8°10'16"	4°5'8"	1:7
1:5	11°25'16"	5°42'38"	1:5
1:3	18°55'29"	9°27'44"	1:3
1:1,866	30°	15°	30°
1:1,207	45°	22°30'	45°
1:0,866	60°	30°	60°
1:0,652	75°	37°30'	75°
1:0,500	90°	45°	90°
1:0,289	120°	60°	120°

К оглавлению

glavconstructor.ru

Уклон и Конусность - Определение, обозначение на чертеже, формула расчёта уклона и конусности

Иногда, в задачах по начертательной геометрии или работах по инженерной графике, или при выполнении других чертежей, требуется построить уклон и конус. В этой статье Вы узнаете о том, что такое уклон и конусность, как их построить, как правильно обозначить на чертеже.

Что такое уклон? Как определить уклон? Как построить уклон? Обозначение уклона на чертежах по ГОСТ.

Уклон. Уклон это отклонение прямой линии от вертикального или горизонтального положения.Определение уклона. Уклон определяется как отношение противолежащего катета угла прямоугольного треугольника к прилежащему катету, то есть он выражается тангенсом угла а. Уклон можно посчитать по формуле i=AC/AB=tga.

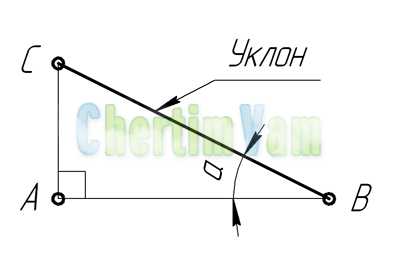
Построение уклона. На примере (рисунок ) наглядно продемонстрировано построение уклона. Для построения уклона 1:1, например, нужно на сторонах прямого угла отложить произвольные, но равные отрезки. Такой уклон, будет соответствовать углу в 45 градусов. Для того чтобы построить уклон 1:2, нужно по горизонтали отложить отрезок равный по значению двум отрезкам отложенным по вертикали. Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а.

Обозначение уклона на чертежах. Обозначение уклонов на чертеже выполняется в соответствии с ГОСТ 2.307—68. На чертеже указывают величину уклона с помощью линии-выноски. На полке линии-выноски наносят знак и величину уклона. Знак уклона должен соответствовать уклону определяемой линии, то есть одна из прямых знака уклона должна быть горизонтальна, а другая должна быть наклонена в ту же сторону, что и определяемая линия уклона. Угол уклона линии знака примерно 30°.

Что такое конусность? Формула для расчёта конусности. Обозначение конусности на чертежах.

Конусность. Конусностью называется отношение диаметра основания конуса к высоте. Конусность рассчитывается по формуле К=D/h, где D – диаметр основания конуса, h – высота. Если конус усеченный, то конусность рассчитывается как отношение разности диаметров усеченного конуса к его высоте. В случае усечённого конуса, формула конусности будет иметь вид: К = (D-d)/h.

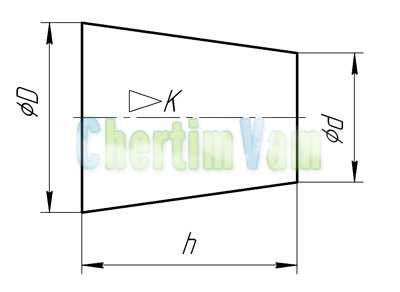
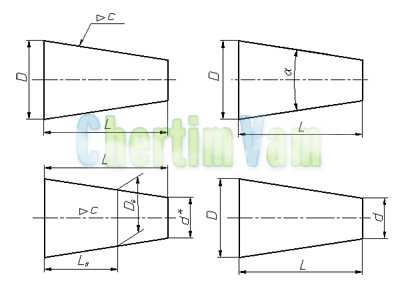
Обозначение конусности на чертежах. Форму и величину конуса определяют нанесением трех из перечисленных размеров: 1) диаметр большого основания D; 2) диаметр малого основания d; 3) диаметр в заданном поперечном сечении Ds , имеющем заданное осевое положение Ls; 4) длина конуса L; 5) угол конуса а; 6) конусность с . Также на чертеже допускается указывать и дополнительные размеры, как справочные.

Размеры стандартизованных конусов не нужно указывать на чертеже. Достаточно на чертеже привести условное обозначение конусности по соответствующему стандарту.

Конусность, как и уклон, может быть указана в градусах, дробью (простой, в виде отношения двух чисел или десятичной), в процентах.Например, конусность 1:5 может быть также обозначена как отношение 1:5, 11°25’16», десятичной дробью 0,2 и в процентах 20.Для конусов, которые применяются в машиностроении, OCT/BKC 7652 устанавливает ряд нормальных конусностей. Нормальные конусности — 1:3; 1:5; 1:8; 1:10; 1:15; 1:20; 1:30; 1:50; 1:100; 1:200. Также в могут быть использованы — 30, 45, 60, 75, 90 и 120°.

chertimvam.ru

Конусность | Начертательная геометрия - nGeo.FXYZ.ru

Конусность - отношение разности диаметров двух поперечных сечений кругового конуса к расстоянию между ними.

$ κ =\frac{D-d}{l} = 2tgφ = 2i $

Конусность имеет двойной Уклон: k=2i Конусность на чертеже может быть указана в градусной мере, в радианах и в процентах. Заданы конусность пробки крана 1:5, диаметр D=BC=20 мм, длина l=35 мм.

Конусность

Необходимо построить очертание пробки крана одним из двух способов: Первый способ. Из формулы k=2i находим i=1:10. Отмечаем точки BC и строим треугольник DKP так, чтобы KP:BK=1:10. Продолжив BP до пересечения с осью конуса, получим вершину конуса S. Точку S соединяем с точкой C. Отложив по оси пробки от BC отрезок l=35 мм и проведя через конец этого отрезка прямую, перпендикулярную к оси , получим диаметр d=EF=13 мм торца пробки; Второй способ. Из формулы k=(D-d)/l находим d=EF=20-35/5=13 мм; Величина угла при вершине конуса:

здесь угол φ представлен в радианах.

где L - расстояние от большого сечения до вершины S конуса, а отношение: D/(2L) = tgφ Пусть задана конусность например 1 : 2,5 откуда i=1:5 и tgφ=0,2 тогда перевод ее в градусы выполняется по формулам:

$ φ=arctgφ=arctg(0,2)=0.1974 [рад] $

$ φ=\frac{0.1974×180°}{π}=11.3102° $

Конусность стандартизована. ГОСТ 8593-81 устанавливает нормальные конусности и углы конусов

Обозна-чение	конуса	Конус-	ность	Угол	конуса	Угол	уклона
Ряд 1	Ряд 2			Угл. ед.	Рад.	Угл. ед.	Рад.
1:500		1:500	0,0020000	6`52,5"	0,0020000	3`26,25"	0,0010000
1:200		1:200	0,0050000	17`11,3"	0,0050000	8`25,65"	0,0025000
1:100		1:100	0,0100000	34`22,6"	0,0100000	17`11,3"	0,0050000
1:50		1:50	0,0200000	1°8`45,2"	0,0199996	34`22,6"	0,0099998
	1:30	1:30	0,0333333	1°54`34,9"	0,0333304	57`17,45"	0,0166652
1:20		1:20	0,0500000	2°51`51,1"	0,0499896	1°25`55,55"	0,0249948
	1:15	1:15	0,0666667	3°49`5,9"	0,0666420	1°54`32,95"	0,0333210
	1:12	1:12	0,0833333	4°46`18,8"	0,0832852	2°23`9,4"	0,0416426
1:10		1:10	0,1000000	5°43`29,3"	0,0999168	2°51`44,65"	0,0499584
	1:8	1:8	0,1250000	7°9`9,6"	0,1248376	3°34`34,8"	0,0624188
	1:7	1:7	0,1428571	8°10`16,4"	0,1426148	4°5`8,2"	0,0713074
	1:6	1:6	0,1666667	9°31`38,2"	0,1662824	4°45`49,1"	0,0831412
1:5		1:5	0,2000000	11°25`16,3"	0,1993374	5°42`38,15"	0,0996687
	1:4	1:4	0,2500000	14°15`0,1"	0,2487100	7°7`30,05"	0,1243550
1:3		1:3	0,3333333	18°55`28,7"	0,3302972	9°27`44,35"	0,1651486
30°		1:1,866025	0,5358985	30°	0,5235988	15°	0,2617994
45°		1:1,207107	0,8284269	45°	0,7853982	22°30`	0,3926991
60°		1:0,866025	1,1547010	60°	1,0471976	30°	0,5235988
	75°	1:0,651613	1,5346532	75°	1,3089970	37°30`	0,6544985
90°		1:0,500000	2,0000000	90°	1,5707964	45°	0,7853982
120°		1:0,288675	3,4641032	120°	2,0943952	60°	1,0471976

Конусности и углы конусов должны соответствовать указанным на чертеже и в таблице. При выборе конусностей или углов конусов ряд 1 следует предпочитать ряду 2.

Конусность поверхности

Конусность

обозначается на чертеже: - надписью Конусность с указанием ее величины; - указывающей на нее стрелкой с полкой где пишется: - Конусность с указанием ее величины; - знак конусности и ее величина.

ngeo.fxyz.ru

Онлайн калькулятор: Конус

Конус - трехмерная фигура, имеющая одно основание и одну вершину.

Косой конусПравильный конус

Косой конус - конус у которого вершина не находится по центру основания.Правильный конус имеет вершину четко выровненную по центру основания. Основание правильного конуса не обязательно должно быть кругом.

Объем конуса: , где __ площадь основания конуса, -кратчайшее расстояние от вершины конуса до основания.

Конус

Если основание правильного конуса - круг, то такой конус будет правильным круговым конусом.Такой конус характеризуется радиусом основания и высотой- расстоянием от вершины до центра основания. Объем правильного кругового конуса:

Площадь поверхности конуса выражается следующей формулой: , где - наклонная высота конуса, измеряемая как расстояние от вершины конуса до любой точки на периметре основания.

Точность вычисления

Знаков после запятой: 5

Площадь боковой поверхности

Площадь поверхности

Сохранить share extension

Схема усеченного правильного конусаПравильный усеченный конус

Объем правильного кругового усеченного конуса Площадь поверхности правильного усеченного конуса

Точность вычисления

Знаков после запятой: 5

Площадь боковой поверхности

Площадь поверхности

planetcalc.ru

Радиус и высота конуса | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU

Через радиус конуса можно найти все параметры конуса, связанные с основанием, а значение высоты позволяет вычислить площади, объемы и все остальные объемные параметры конуса. Так, диаметр конуса равен удвоенному радиусу, периметр окружности в основании вычисляется по стандартной формуле через радиус, равно как и площадь основания. d=2r P=2πr S_(осн.)=πr^2

Прямоугольный треугольник, образованный высотой конуса, радиусом основания и образующей конуса, связывает эти три значения теоремой Пифагора, по которой можно вычислить неизвестную образующую, а также угол между образующей и основанием. Тем временем, угол α рассчитывается из равнобедренного треугольника, сформированного двумя образующими и диаметром из того принципа, что сумма всех углов в треугольнике равна 180 градусам. (рис.40.1, 40.2) l=√(h^2+r^2 ) tan⁡β=h/r α=180°-2β

Чтобы найти площадь боковой поверхности конуса, необходимо умножить радиус и апофему на число π. Площадь полной поверхности конуса состоит из площади его основания и площади боковой поверхности. В обеих формулах вместо апофемы нужно подставить квадратный корень через высоту и радиус, полученный по теореме Пифагора. S_(б.п.)=πrl=πr√(h^2+r^2 ) S_(п.п.)=S_(б.п.)+S_(осн.)=πrl+πr^2=πr(l+r)=πr(√(h^2+r^2 )+r)

Чтобы найти объем конуса, достаточно знать значения радиуса и высоты, тогда формула объема выглядит как произведение числа π на квадрат радиуса и высоту, деленное на три. V=1/3 S_(осн.) h=(πr^2 h)/3

Радиус сферы, вписанной в конус, зависит не только от радиуса основания конуса и его высоты, но и от образующей, поэтому чтобы вычислить радиус вписанной сферы конуса через радиус конуса и высоту, нужно вместо образующей подставить полученное для нее выше выражение. Радиус описанной сферы может быть представлен сразу формулой только с переменными радиуса и высоты. (рис.40.3, 40.4) r_1=hr/(l+r)=rh/(√(h^2+r^2 )+r) R=(h^2+r^2)/2h

geleot.ru

радиус основанияконуса равен 12, образующая 40. найти угол развертки конуса.

Пусть угол развёртки равен φ. Произведение длины образующей на угол развёртки равно длине окружности основания: 40φ = 2π•12 ⇒ φ = 3π/5 = 0,6π (= 108°) ОТВЕТ: 3π/5, или 108°

Ответ: 2*arcsin(12/40)=2*arcsin(0.3)

Если радиус основания конуса 12, то длина окружности 2п*12 = 24п. Развертка конуса - круговой сектор, радиус которого равен 40, длина дуги 24п, угол n градусов. Имеем: 24п = 40пn / 180 24 = 2n /9 отсюда n = 12*9 =108 градусов Ответ: 108

touch.otvet.mail.ru

Конус. Усеченный конус

Конической поверхностью называется поверхность, образованная всеми прямыми, проходящими через каждую точку данной кривой и точку вне кривой (рис.32).

Данная кривая называется направляющей, прямые – образующими, точка – вершиной конической поверхности.

Прямой круговой конической поверхностью называется поверхность, образованная всеми прямыми, проходящими через каждую точку данной окружности и точку на прямой, которая перпендикулярна плоскости окружности и проходит через ее центр. В дальнейшем эту поверхность будем кратко называть конической поверхностью (рис.33).

Конусом (прямым круговым конусом) называется геометрическое тело, ограниченное конической поверхностью и плоскостью, которая параллельна плоскости направляющей окружности (рис.34).

Рис. 32 Рис. 33 Рис. 34

Конус можно рассматривать как тело, полученное при вращении прямоугольного треугольника вокруг оси, содержащей один из катетов треугольника.

Круг, ограничивающий конус, называется его основанием. Вершина конической поверхности называется вершиной конуса. Отрезок, соединяющий вершину конуса с центром его основания, называется высотой конуса. Отрезки, образующие коническую поверхность, называются образующими конуса. Осью конуса называется прямая, проходящая через вершину конуса и центр его основания. Осевым сечением называется сечение, проходящее через ось конуса. Разверткой боковой поверхности конуса называется сектор, радиус которого равен длине образующей конуса, а длина дуги сектора равна длине окружности основания конуса.

Для конуса верны формулы:

(7)

где R – радиус основания;

H – высота;

l – длина образующей;

Sосн – площадь основания;

Sбок – площадь боковой поверхности;

Sполн – площадь полной поверхности;

V – объем конуса.

Усеченным конусом называется часть конуса, заключенная между основанием и секущей плоскостью, параллельной основанию конуса (рис.35).

Рис. 35

Усеченный конус можно рассматривать как тело, полученное при вращении прямоугольной трапеции вокруг оси, содержащей боковую сторону трапеции, перпендикулярную основаниям.

Два круга, ограничивающие конус, называются его основаниями. Высотой усеченного конуса называется расстояние между его основаниями. Отрезки, образующие коническую поверхность усеченного конуса называются образующими. Прямая, проходящая через центры оснований, называется осью усеченного конуса. Осевым сечением называется сечение, проходящее через ось усеченного конуса.

Для усеченного конуса верны формулы:

(8)

где R – радиус нижнего основания;

r – радиус верхнего основания;

H – высота, l – длина образующей;

Sбок – площадь боковой поверхности;

Sполн – площадь полной поверхности;

V – объем усеченного конуса.

Пример 1.Сечение конуса параллельное основанию делит высоту в отношении 1:3, считая от вершины. Найти площадь боковой поверхности усеченного конуса, если радиус основания и высота конуса равны 9 см и 12 см.

Решение. Сделаем рисунок (рис. 36).

Для вычисления площади боковой поверхности усеченного конуса используем формулу (8). Найдем радиусы оснований О1А и О1В и образующую АВ.

Рассмотрим подобные треугольники SO2B и SO1A, коэффициент подобия , тогда

Отсюда

Из SO1A

Так как то

Площадь боковой поверхности усеченного конуса равна:

Ответ: .

Пример2. Четверть круга радиуса свернута в коническую поверхность. Найти радиус основания и высоту конуса.

Решение.Четверить круга является разверткой боковой поверхности конуса. Обозначим r – радиус его основания, H – высота. Площадь боковой поверхности вычислим по формуле: . Она равна площади четверти круга: . Получим уравнение с двумя неизвестными r и l (образующая конуса). В данном случае образующая равна радиусу четверти круга R, значит, получим следующее уравнение: , откуда Зная радиус основания и образующую, найдем высоту конуса:

Ответ: 2 см, .

Пример 3. Прямоугольная трапеция с острым углом 45О, меньшим основанием 3см и наклонной боковой стороной равной , вращается вокруг боковой стороны перпендикулярной основаниям. Найти объем полученного тела вращения.

Решение.Сделаем рисунок (рис. 37).

В результате вращения получим усеченный конус, чтобы найти его объем вычислим радиус большего основания и высоту. В трапеции O1O2AB проведем AC^O1B. В имеем: значит, этот треугольник равнобедренный AC=BC=3 см.

Ответ:

Пример 4.Треугольник со сторонами 13 см, 37 см и 40 см вращается вокруг внешней оси, которая параллельна большей стороне и находится от нее на расстоянии 3 см (Ось расположена в плоскости треугольника). Найти площадь поверхности полученного тела вращения.

Решение. Сделаем рисунок (рис. 38).

Поверхность полученного тела вращения состоит из боковых поверхностей двух усеченных конусов и боковой поверхности цилиндра. Для того чтобы вычислить эти площади необходимо знать радиусы оснований конусов и цилиндра (BE и OC), образующие конусов (BC и AC) и высоту цилиндра (AB). Неизвестной является только CO. это расстояние от стороны треугольника до оси вращения. Найдем DC. Площадь треугольника ABC с одной стороны равна произведению половины стороны AB на высоту , проведенную к ней DC, с другой стороны, зная все стороны треугольника, его площадь вычислим по формуле Герона:

Но

Из этих равенств находим Подставляя найденные значения, получаем:

Таким образом, площадь поверхности тела вращения равна

Ответ: см2.

Пример 5. Два конуса имеют общую высоту, но вершины их лежат в разных концах высоты. Образующая первого конуса равна l, а угол при вершине его осевого сечения равен 2a. Угол при вершине осевого сечения второго конуса равен 2b.Найти объем общей части конусов.

Решение.Сделаем рисунок (рис. 39).

Объем общей части конусов равен сумме объемов конуса с общим основанием радиуса ВА, высотой BD и высотой BC соответственно. Получим следующее выражение для вычисления объема:

Рассмотрим первый конус, у которого образующая DF равна l, а угол при вершине осевого сечения Треугольник CDF прямоугольный, , тогда Из треугольника BDA ( ) выразим DB: из треугольника BCA ( ) выразим BC:

Получим следующее: или Из этих равенств выразим AB: Þ

Подставив найденные выражения в формулу для вычисления объема, получим: