Инжинерная графика,начертательная геометрия, лекции / Курс лекций по ИКГ. Принцип работы икг
Графическое представление результатов измерений
Для наглядного представления взаимной связи физических величин и их закономерного изменения результата наблюдений представляют графически.
Чаще всего используют прямоугольную систему координат. По оси абсцисс в произвольном масштабе откладывают независимую переменную, т.е. величину, значения которой задает сам экспериментатор. а по оси ординат ту величину, которую он при этом определяет. При выборе масштаба нужно исходить из следующих соображений: I) экспериментальные точки не должны сливаться друг с другом, т.е. они должны располагаться с разумным интервалом; 2) масштаб должен быть удобным. Проще всего, если I см соответствует 1,2,5,10,100,0.1 и т.д. единицам измеренной величины.
На осях координат следует указывать название или символ величины. Обязательно нужно также указывать единицы измерений, причем десятичный множитель следует отнести к единице измерения. Тогда деления на графике можно помечать цифрами 1,2,3... или 10,20.30 ..., а не 10000, 20000 ... и т.д. или 0.0001, 0,0002 и т.д. Экспериментальные данные следует отмечать "жирными", хорошо выделяющимися точками. По полученным на плоскости точкам проводят "наилучшую " плавную (неломаную) кривую (рис-6), которая может проходить не через все отмеченные точки, а близко к ним. Такая кривая дает нам возможность проводить графическим путем интерполяцию, т.е. находить значения У даже для таких значений X, которые непосредственно не наблюдались.
Если полученные данные не образуют прямой на линейной (миллиметровой) графической бумаге, то можно попытаться построить график в логарифмических координатах (или наносить логарифмы значений Х и У на линейную графическую бумагу). В логарифмических координатах график простой, но важной функции
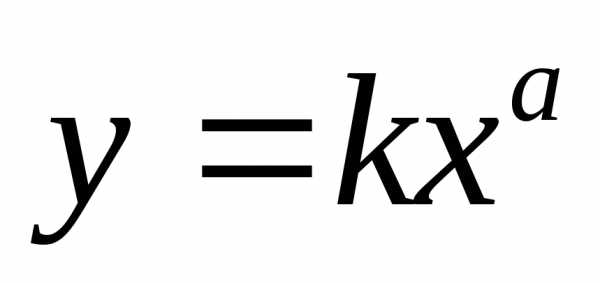 (62)
(62)
имеет вид прямой. Переходя к логарифмам, действительно, получаем уравнение прямой:
где К и а - постоянные.
Имеется также третий тип графической бумаги -полулогарифмическая, когда одна шкала является лога-рифмической, а другая -линейной. В этом случае получается прямая, если данные подчиняются закону
Рис.6
(64)После преобразований этой функции имеем
(65)
Чтобы получилась прямая, шкала по оси У должна быть логарифмической, а по оси х – линейной.
Лабораторная работа 102 измерение линейных размеров оптиметром икг
Цель работы: ознакомиться с устройством горизонтального оптиметра ККГ, провести измерение толщины алюминиевой фольги и статистическую обработку результатов прямого измерения.
Назначение и устройство ИКГ. Оптиметр - оптикомеханический прибор, который служит для измерения линейных размеров абсолютным (в пределах шкалы) или относительным (сравнением о концевой мерой мины) методами. На горизонтальном оптиметре можно производить измерения толщины пластинок, диаметра шариков, внутренних диаметров.
ИКГ состоит из массивного штатива I (рио.1), на котором укреплены предметный столик 2, оптическая труба 3 с оптическим отсчетным устройством. В левой части трубы укреплен штифт 4, соприкасающийся с поверхностью измеряемого изделия. Отсчеты при измерении снимают по шкале окуляра 5,6 - пиноль-металлическая труба, внутри которой помещается стержень 9 с пружиной. Стержень может перемещаться вдоль оси вращением винта 7,
а положение наконечника 9 закрепляется винтом 8. Составной частью оптиметра является проекционное устройство ПН-6.

Рис. I
Оптическая труба оптиметра - основная часть прибора (рис.2). Световой поток источника S , отражаясь от зеркала 3 и призмы П1 (явление полного внутреннего отражения), освещает шкалу Ш, которая находится в фокальной плоскости объектива ОБ и через окуляр ОК не видна, так как она закрыта призмой П1. Пройдя через призму П2 и объектив ОЕ, лучи падают на зеркало З2, в котором изображается шкала Ш. При отражении лучей от зеркала З2 изображение шкалы И по принципу автоколлимации создается объективом рядок с самой шкалой Ш так, что нулевой штрих совпадает с неподвижным указателем у .
Наблюдение ведется через окуляр ОК. Если совпадения нет, то его можно добиться смещением штифта 4 винтом 7 (см-рис.1). Измеряемая деталь, помещенная между наконечниками 4 и 9 (см.рис. I и 2), приведет к поступательному перемещению штифта 4, который повернет плоское зеркало З2 на угол φ .Изображение шкалы И смещается параллельно шкале Ш; величина смещения отсчитывается относительно неподвижного указателя.
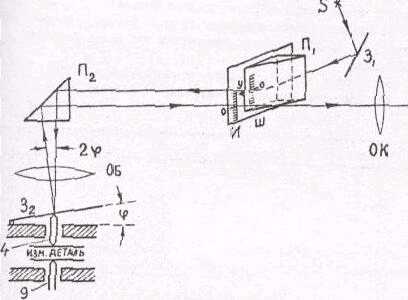
Рис. 2
Механические и оптические соотношения системы оптиметра подобраны так, что видимое в окуляр смещение изображения шкалы на одно деление соответствует осевому перемещению штифта на один микрон, т.е. цена деления прибора - I мк.
studfiles.net
Графическое представление результатов измерений
Для наглядного представления взаимной связи физических величин и их закономерного изменения результата наблюдений представляют графически.
Чаще всего используют прямоугольную систему координат. По оси абсцисс в произвольном масштабе откладывают независимую переменную, т.е. величину, значения которой задает сам экспериментатор. а по оси ординат ту величину, которую он при этом определяет. При выборе масштаба нужно исходить из следующих соображений: I) экспериментальные точки не должны сливаться друг с другом, т.е. они должны располагаться с разумным интервалом; 2) масштаб должен быть удобным. Проще всего, если I см соответствует 1,2,5,10,100,0.1 и т.д. единицам измеренной величины.
На осях координат следует указывать название или символ величины. Обязательно нужно также указывать единицы измерений, причем десятичный множитель следует отнести к единице измерения. Тогда деления на графике можно помечать цифрами 1,2,3... или 10,20.30 ..., а не 10000, 20000 ... и т.д. или 0.0001, 0,0002 и т.д. Экспериментальные данные следует отмечать "жирными", хорошо выделяющимися точками. По полученным на плоскости точкам проводят "наилучшую " плавную (неломаную) кривую (рис-6), которая может проходить не через все отмеченные точки, а близко к ним. Такая кривая дает нам возможность проводить графическим путем интерполяцию, т.е. находить значения У даже для таких значений X, которые непосредственно не наблюдались.
Если полученные данные не образуют прямой на линейной (миллиметровой) графической бумаге, то можно попытаться построить график в логарифмических координатах (или наносить логарифмы значений Х и У на линейную графическую бумагу). В логарифмических координатах график простой, но важной функции
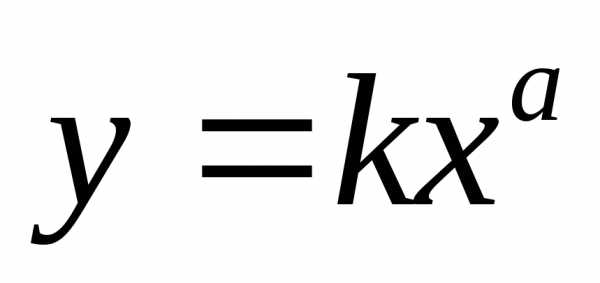 (62)
(62)
имеет вид прямой. Переходя к логарифмам, действительно, получаем уравнение прямой:
где К и а - постоянные.
Имеется также третий тип графической бумаги -полулогарифмическая, когда одна шкала является лога-рифмической, а другая -линейной. В этом случае получается прямая, если данные подчиняются закону
Рис.6
(64)После преобразований этой функции имеем
(65)
Чтобы получилась прямая, шкала по оси У должна быть логарифмической, а по оси х – линейной.
Лабораторная работа 102 измерение линейных размеров оптиметром икг
Цель работы: ознакомиться с устройством горизонтального оптиметра ККГ, провести измерение толщины алюминиевой фольги и статистическую обработку результатов прямого измерения.
Назначение и устройство ИКГ. Оптиметр - оптикомеханический прибор, который служит для измерения линейных размеров абсолютным (в пределах шкалы) или относительным (сравнением о концевой мерой мины) методами. На горизонтальном оптиметре можно производить измерения толщины пластинок, диаметра шариков, внутренних диаметров.
ИКГ состоит из массивного штатива I (рио.1), на котором укреплены предметный столик 2, оптическая труба 3 с оптическим отсчетным устройством. В левой части трубы укреплен штифт 4, соприкасающийся с поверхностью измеряемого изделия. Отсчеты при измерении снимают по шкале окуляра 5,6 - пиноль-металлическая труба, внутри которой помещается стержень 9 с пружиной. Стержень может перемещаться вдоль оси вращением винта 7,
а положение наконечника 9 закрепляется винтом 8. Составной частью оптиметра является проекционное устройство ПН-6.
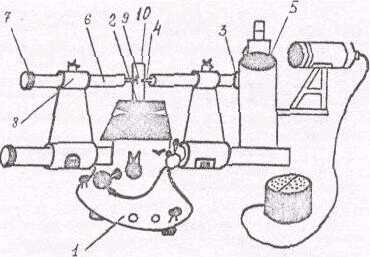
Рис. I
Оптическая труба оптиметра - основная часть прибора (рис.2). Световой поток источника S , отражаясь от зеркала 3 и призмы П1 (явление полного внутреннего отражения), освещает шкалу Ш, которая находится в фокальной плоскости объектива ОБ и через окуляр ОК не видна, так как она закрыта призмой П1. Пройдя через призму П2 и объектив ОЕ, лучи падают на зеркало З2, в котором изображается шкала Ш. При отражении лучей от зеркала З2 изображение шкалы И по принципу автоколлимации создается объективом рядок с самой шкалой Ш так, что нулевой штрих совпадает с неподвижным указателем у .
Наблюдение ведется через окуляр ОК. Если совпадения нет, то его можно добиться смещением штифта 4 винтом 7 (см-рис.1). Измеряемая деталь, помещенная между наконечниками 4 и 9 (см.рис. I и 2), приведет к поступательному перемещению штифта 4, который повернет плоское зеркало З2 на угол φ .Изображение шкалы И смещается параллельно шкале Ш; величина смещения отсчитывается относительно неподвижного указателя.
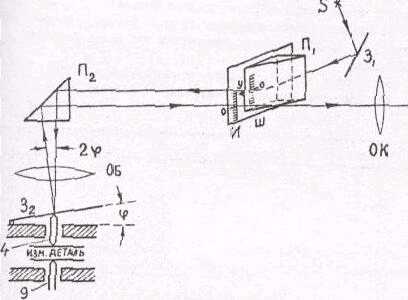
Рис. 2
Механические и оптические соотношения системы оптиметра подобраны так, что видимое в окуляр смещение изображения шкалы на одно деление соответствует осевому перемещению штифта на один микрон, т.е. цена деления прибора - I мк.
studfiles.net
Графическое представление результатов измерений
Для наглядного представления взаимной связи физических величин и их закономерного изменения результата наблюдений представляют графически.
Чаще всего используют прямоугольную систему координат. По оси абсцисс в произвольном масштабе откладывают независимую переменную, т.е. величину, значения которой задает сам экспериментатор. а по оси ординат ту величину, которую он при этом определяет. При выборе масштаба нужно исходить из следующих соображений: I) экспериментальные точки не должны сливаться друг с другом, т.е. они должны располагаться с разумным интервалом; 2) масштаб должен быть удобным. Проще всего, если I см соответствует 1,2,5,10,100,0.1 и т.д. единицам измеренной величины.
На осях координат следует указывать название или символ величины. Обязательно нужно также указывать единицы измерений, причем десятичный множитель следует отнести к единице измерения. Тогда деления на графике можно помечать цифрами 1,2,3... или 10,20.30 ..., а не 10000, 20000 ... и т.д. или 0.0001, 0,0002 и т.д. Экспериментальные данные следует отмечать "жирными", хорошо выделяющимися точками. По полученным на плоскости точкам проводят "наилучшую " плавную (неломаную) кривую (рис-6), которая может проходить не через все отмеченные точки, а близко к ним. Такая кривая дает нам возможность проводить графическим путем интерполяцию, т.е. находить значения У даже для таких значений X, которые непосредственно не наблюдались.
Если полученные данные не образуют прямой на линейной (миллиметровой) графической бумаге, то можно попытаться построить график в логарифмических координатах (или наносить логарифмы значений Х и У на линейную графическую бумагу). В логарифмических координатах график простой, но важной функции
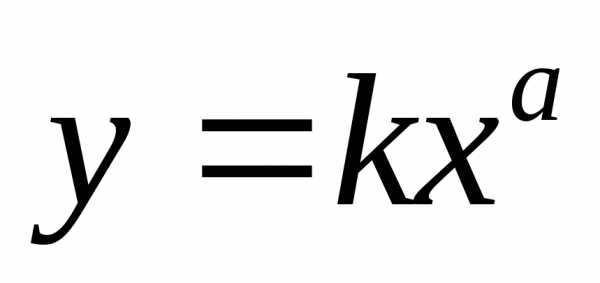 (62)
(62)
имеет вид прямой. Переходя к логарифмам, действительно, получаем уравнение прямой:
где К и а - постоянные.
Имеется также третий тип графической бумаги -полулогарифмическая, когда одна шкала является лога-рифмической, а другая -линейной. В этом случае получается прямая, если данные подчиняются закону
Рис.6
(64)После преобразований этой функции имеем
(65)
Чтобы получилась прямая, шкала по оси У должна быть логарифмической, а по оси х – линейной.
Лабораторная работа 102 измерение линейных размеров оптиметром икг
Цель работы: ознакомиться с устройством горизонтального оптиметра ККГ, провести измерение толщины алюминиевой фольги и статистическую обработку результатов прямого измерения.
Назначение и устройство ИКГ. Оптиметр - оптикомеханический прибор, который служит для измерения линейных размеров абсолютным (в пределах шкалы) или относительным (сравнением о концевой мерой мины) методами. На горизонтальном оптиметре можно производить измерения толщины пластинок, диаметра шариков, внутренних диаметров.
ИКГ состоит из массивного штатива I (рио.1), на котором укреплены предметный столик 2, оптическая труба 3 с оптическим отсчетным устройством. В левой части трубы укреплен штифт 4, соприкасающийся с поверхностью измеряемого изделия. Отсчеты при измерении снимают по шкале окуляра 5,6 - пиноль-металлическая труба, внутри которой помещается стержень 9 с пружиной. Стержень может перемещаться вдоль оси вращением винта 7,
а положение наконечника 9 закрепляется винтом 8. Составной частью оптиметра является проекционное устройство ПН-6.
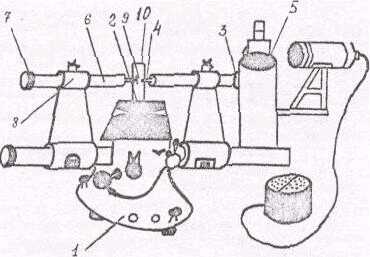
Рис. I
Оптическая труба оптиметра - основная часть прибора (рис.2). Световой поток источника S , отражаясь от зеркала 3 и призмы П1 (явление полного внутреннего отражения), освещает шкалу Ш, которая находится в фокальной плоскости объектива ОБ и через окуляр ОК не видна, так как она закрыта призмой П1. Пройдя через призму П2 и объектив ОЕ, лучи падают на зеркало З2, в котором изображается шкала Ш. При отражении лучей от зеркала З2 изображение шкалы И по принципу автоколлимации создается объективом рядок с самой шкалой Ш так, что нулевой штрих совпадает с неподвижным указателем у .
Наблюдение ведется через окуляр ОК. Если совпадения нет, то его можно добиться смещением штифта 4 винтом 7 (см-рис.1). Измеряемая деталь, помещенная между наконечниками 4 и 9 (см.рис. I и 2), приведет к поступательному перемещению штифта 4, который повернет плоское зеркало З2 на угол φ .Изображение шкалы И смещается параллельно шкале Ш; величина смещения отсчитывается относительно неподвижного указателя.
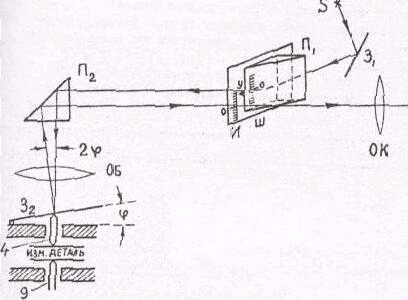
Рис. 2
Механические и оптические соотношения системы оптиметра подобраны так, что видимое в окуляр смещение изображения шкалы на одно деление соответствует осевому перемещению штифта на один микрон, т.е. цена деления прибора - I мк.
studfiles.net
Случайные величины
Случайной величиной называется переменная величина, которая в зависимости от тех или иных, не поддающихся учету обстоятельств может принимать различные численные значения.
К таким величинам относятся, например, скорость хаотического движения молекулы газа, число радиоактивного распада атомов за данный промежуток времени, ошибка измерения физической величина и т.п.
Случайные величины могут быть дискретными и непрерывными. Дискретной называется случайная величина,
принимающая только отдельные числовые значения (например, число молекул в данный момент в некотором элементе объема газа, результаты отдельных измерений Х и т.п.)
Для того, чтобы полностью охарактеризовать случайную дискретную величину, надо перечислить все ее возможные значения и их вероятности. Зависимость между значениями случайной величины Х и их вероятностями
Р(X) представляет закон распределения вероятностей случайной дискретной величины или просто распределение. Она обычно задается в виде таблицы.
| X | X1 | X2 | X3 | … | Xn |
| P(X) | P1 | P2 | P3 | … | Pn |
При этом сумма вероятностей всех возможных значений случайной величины равна единице:
(8)
В примера с кубиком с занумерованными гранями случайная величина может иметь только шесть значений (граней) с равными вероятностями и следовательно,

Параметры распределения случайных величин
Законы распределения являются полными характерис-тиками случайных величин. Но они не всегда удобны для практики. На практике чаще случайную величину характеризуют определенными числовыми параметрами, связанными с законом ее распределения. Основные из них: математическое ожидание и дисперсия. Математическим ожиданием М (X) случайной величины называется сумма произведений всех ее возможных значений на их вероятности:
(9)
Определение математического ожидания требует знания закона распределения вероятностей. Если он не выявлен, то вычисляют среднее арифметическое значение случайной величины X, т.е.
(10)
Согласно закону больших чисел :
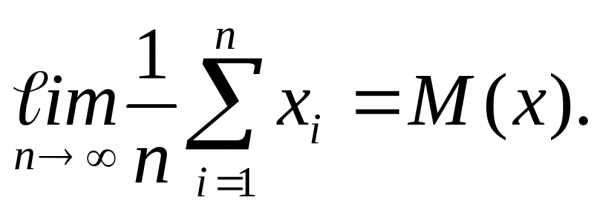 (11)
(11)
Таким образом, математическое ожидание М(х) является центром распределения вероятностей случайной величины Х и оценивается одним числом, т.е. М(х)= Const.
Отдельные значения случайной величины группируются около математического ожидания как центра (см.рис.I). Степень рассеяния или разброса этих значений характеризуют величиной, называемой дисперсией D(х) случайной величины.
Дисперсией D(х) называют математическое ожидание квадрата отклонений возможных значений случайной величины от ее математического ожидания:
(12)
Таким образом, дисперсия предcтавляет средний квадрат отклонений случайной величины от ее математического ожидания. Формулу (12) можно выразить через средние величины в удобной
для вычислений форме:
(13)
Дисперсия имеет размерность квадрата размерности случайной величины. Поэтому для сопоставления и оценки рассеяния возможных значений случайной величины около математического ожидания вводят понятие среднего квадратичного отклонения, имеющего в отличие от дисперсии такую же размерность, как и случайная величина.
Средним квадратичным отклонением σ случайной величины называют корень квадратный из дисперсии:
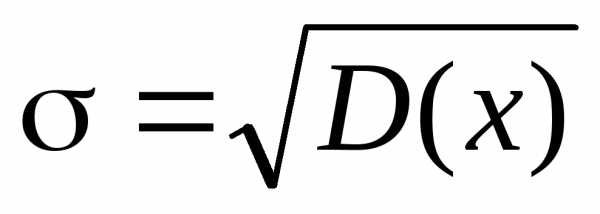 (14)
(14)
В теории ошибок σ называют средней квадратичной ошибкой.
studfiles.net
7.1.1 Описание метода и средства измерения
Для измерения калибров-скоб используются приборы высокой точности: миниметры, оптиметры и т. д. В данной работе измерение калибра-скобы производится на горизонтальном оптиметре типа ИКГ. Это прибор рычажно-оптической системы, предназначен для измерения наружных и внутренних размеров методом сравнения с мерой (относительный метод). Метрологические характеристики горизонтального оптиметра приведены в табл. 7.2.
Таблица 7.2 - Метрологические характеристики горизонтального оптиметра
| Наименование показателей | Числовое значение показателей, мм |
| Наибольшая длина измеряемого изделия | 300 |
| Пределы измерения внутренних размеров | 13,3 - 150 |
| Цена деления шкалы | 0,001 |
| Пределы измерения шкалы | ±0,100 |
| Погрешность показаний при измерении наружных размеров | ±0,0003 |
| Погрешность показаний при измерении внешних размеров | ±0,001 |
7.1.2 Устройство и принцип действия горизонтального оптиметра
Оптическая схема трубки оптиметра показана на рис.7.3. В нее входят: зеркало, объектив, призма полного внутреннего отражения, сетка и окуляр
Осветительную систему составляют зеркало в оправе и призма, установленная в рамке окуляра.
Сетка представляет собой стеклянную плоскопараллельную пластинку со шкалой и удлиненным штриховым индексом, причем деления шкалы нанесены на одной половине пластинки, а индекс — на другой. Шкала со стороны окуляра закрыта призмой так, что через окуляр можно видеть только индекс и изображение шкалы, отраженное от зеркала.
Лучи света, отражаясь от осветительного зеркала, через призму осветительной системы освещают шкалу; пройдя призму и объектив, они параллельным пучком падают на зеркало, отражаются от него и возвращаются
в объектив, снова проходя призму, сетку и попадают в окуляр. При осевом перемещении измерительного штифта трубки оптиметра зеркало будет отклоняться на некоторый угол φ, вследствие чего изображение шкал в поле зрения окуляра будет перемещаться относительно неподвижного индекса.
При установке окуляра по глазу наблюдателя; видно одновременно изображение шкалы и индекса.
Оптическая схема оптиметра ИКГ-3
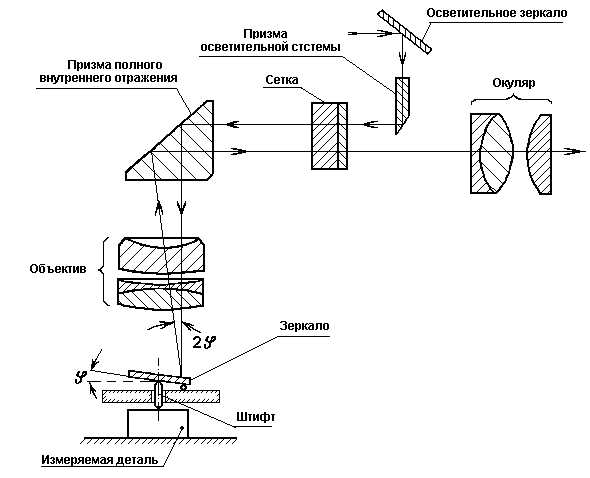
Рис. 7.3
Между величиной перемещения измерительного штифта и величиной перемещения изображения шкалы существует следующая зависимость:
перемещение штифта на величину h (рис. 7.4) вызывает наклон зеркала на угол φ величина которого определяется из отношения
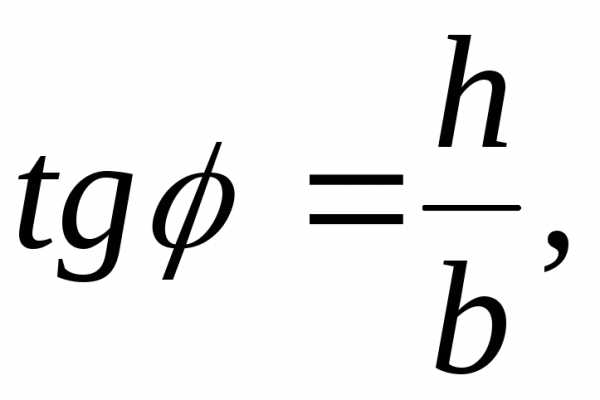 /7,1/
/7,1/
где b — длина плеча, равная расстоянию от оси вращения зеркала до точки касания штифта.
Луч MN при отражении от зеркала отклонится на угол 2φ и точка М вследствие этого переместится в точку М1.
Схема соотношения между величиной перемещения измерительного штифта и величиной перемещения изображения шкалы
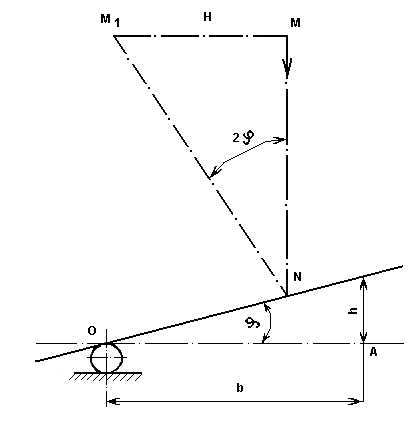
Рис. 7.4
Из треугольника MNM1 имеем:
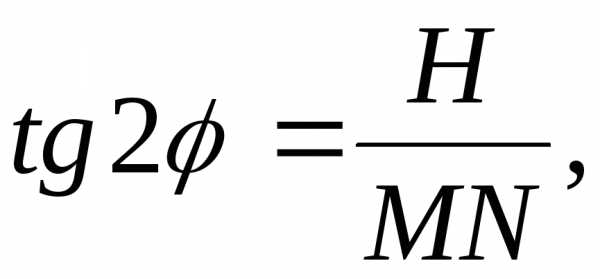 /7,2/
/7,2/
где H – величина перемещения изображения шкалы;
MN – фокусное расстояние объектива.
Так как углы φ и 2φ малы, то значения tgφ tg2φ можно заменить значениями этих углов, тогда:
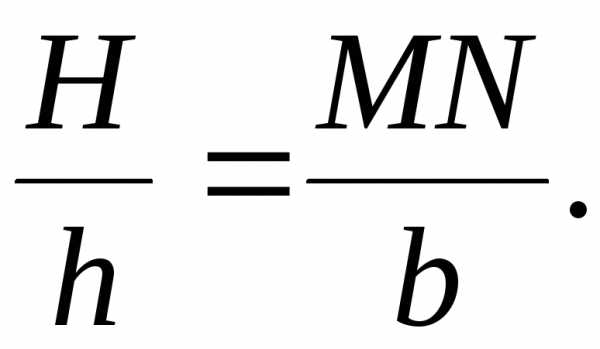 /7,3/
/7,3/
Полученное соотношение является передаточным отношением между величиной перемещения измерительного штифта и величиной перемещения изображения шкалы.
На рис. 7.5 показаны шкала и удлиненный штриховой индекс, видимые в поле зрения трубки оптиметра. Шкала имеет 100 делений с каждой стороны от нуля, расположенных симметрично.
Видимое в окуляр смещение шкалы на одно деление соответствует осевому перемещению измерительного штифта на 0,001 мм.
Общий вид прибора показан на рис. 7.6.
Шкала, видимая в окуляр
Рис. 7.5
Оптиметр горизонтальный ИКГ-3, общий вид
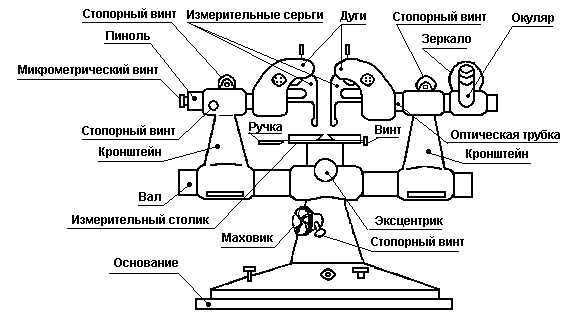
Рис. 7.6
Основными узлами прибора являются основание с установленными на нем измерительным столиком и валом. На валу с помощью кронштейнов закреплены дуги с подвижными измерительными серьгами. Оптическая трубка расположена на правом кронштейне. Перемещение серьги вызывает перемещение шкалы в окуляре. Измерительный столик может перемещаться в вертикальной плоскости при вращении маховика и в горизонтальной плоскости при вращении винта на измерительном столике. Ручкой на измерительном столике можно повернуть столик на угол вокруг вертикальной оси, а эксцентриком можно повернуть столик вокруг горизонтальной оси (при этом стопорные винты должны быть ослаблены).
При работе с оптиметром можно использовать различные приспособления, которые позволяют измерять наружные и внутренние линейные размеры изделий.
Оптиметр должен работать в сухом и чистом помещении при отсутствии тряски и вибраций. При измерениях необходимо соблюдать строгий температурный режим. Отклонения температуры от нормальной (20оС) не должны превышать ±2оС, а при особо важных измерениях ±0,5оС. Перед работой необходимо проверить установку по горизонту по круговому уровню.
studfiles.net
Измерение размеров и контроль качества поверхностей деталей оптико-механическим способом, страница 22
Все полученные показания прибора заносятся в бланк отчёта. Сравнивая действительные размеры проходной и непроходной сторон калибра-пробки, полученные путём измерения, с допустимыми предельными размерами по ГОСТ 24853-81 и ГОСТ 24852-81 дать заключение о годности каждой стороны калибра-пробки отдельно.
Определить отклонение от правильной геометрической формы: овальность – как наибольшую разность размеров диаметра, измеренного в двух взаимно перпендикулярных направлениях одного сечения; конусность, бочкообразность (или вогнутость) – как наибольшую разность размеров диаметров, измеренных в двух различных сечениях.
Библиографический список
1. Белкин И. М. Допуски и посадки. М.: Машиностроение, 1992.
2. Ганевский Г. М., Гольдин И. И. Допуски, посадки и технические измерения. М.: Машиностроение, 1993.
3. Медовый И. А. и др. Исполнительные размеры калибров: Справочник. М.: Машиностроение, 1980.
Лабораторная работа № 5
ИЗМЕРЕНИЕ ВНУТРЕННИХ РАЗМЕРОВ ОПТИМЕТРОМ ИКГ
Цель работы: ознакомление с конструкцией горизонтального оптиметра ИКГ, с приёмами измерения на нём внутренних размеров и выдача на основании измерений заключения о годности измеряемой детали. Кроме этого, настоящая работа имеет своей целью также закрепление полученных на лекциях основных понятий об отечественной системе допусков на изготовление деталей и внутренних колец подшипников качения.
Принцип действия и оптическая система прибора
Принцип действия и оптическая система прибора ИКГ описана в работе № 4. В данном случае измерение внутренних диаметров производится наконечниками серёг 26, закруглённых на дугах 25. Закрепление серёг на осях дуг производится с помощью винтов 27 (рис. 1).
Порядок выполнения работы
При измерении внутренних размеров в качестве образцовой меры применяется калибр-скоба, составленная из блока концевых мер и особых боковичков, притираемых к блоку по концам и закреплённых в специальной державке.
Измерение производится в следующем порядке.
1. Установить основание прибора 1 (рис. 1) в горизонтальное положение с помощью регулировочных винтов 10 и круглого уровня 11.
2. Сдвинуть кронштейны 5 и 6, освободив предварительно их стопорные винты 12 так, чтобы выступ левой серьги 26 вошел в паз правой серьги.
ПРИМЕЧАНИЕ. Для сокращения затраты времени на настройку прибора взаимное положение дуг оптиметра и пиноли отрегулировано заранее. Поэтому стопорные винты 13 и 14 трогать не следует. Передвижение пиноли и трубки оптиметра производить только совместно с кронштейном 5 и 6.

Рис. 1. Общий вид оптиметра ИКГ для измерения внутренних размеров: 1 - основание прибора, 2 - трубка оптиметра, 3 - пиноль, 4 - проекционное устройство, 5, 6 - кронштейны, 7 - стол, 9 - трансформатор, 10 - регулировочный винт, 11 - круглый уровень, 12, 13, 14, 15 - стопорные винты, 16 - маховичок, 17 - стопорный винт, 18 - головка микрометрического винта, 19, 20 - рукоятки, 21 - стопорный винт, 22 - арретир, 23 - кремальера, 25 - серьга, 27 - винт
3. На середину стола 7 положить образцовую калибр-скобу, размер которой соответствует номинальному размеру проверяемого отверстия, и закрепить с помощью струбцин. При этом рабочие поверхности калибр-скобы должны быть перпендикулярны к линии измерения размера.
4. Отстопорить винт 15 и с помощью маховичка 16 поднять стол 7 так, чтобы внутренние поверхности боковичков калибр-скобы были на одной оси с измерительными наконечниками, находящимися на серьгах 26, т. е. необходимо поднять стол до уровня линии измерения. Застопорить столик винтом 15.
5. Поворотом кремальеры 23 переместить верхнюю площадку стола так, чтобы серьги 26 с измерительными наконечниками оказались внутри боковичков калибр-скобы.
6. Отодвинуть кронштейн 6 с пинолью так, чтобы наконечник слегка коснулся боковичка калибр-скобы. Застопорить кронштейн 6 винтом 12. Следить при этом, чтобы верхняя площадка стола свободно перемещалась в обе стороны вдоль линии измерения.
vunivere.ru
Курс лекций по ИКГ
графические материалов и правила их нанесения на чертежах»; ГОСТ 2.307-68*«Нанесение размеров и предельных отклонений»; ГОСТ2.311-68«Изображение резьбы»; ГОСТ2.316-2008«Правила нанесения на чертежах надписей, технических требований и таблиц»; ГОСТ2.317-69«Аксонометрические проекции».
1.1.1. Изделия
Объект производства, для изготовления которого выполняют конструкторскую документацию, определяют термином «изделие».
Изделие – предмет или совокупность предметов производства, подлежащих изготовлению на предприятии. В зависимости от назначения различают изделия основного и вспомогательного производства. Изделие, предназначенное для поставки заказчику (потребителю), относят к изделиям основного производства; изделие, предназначенное для обеспечения собственных нуждпредприятия-изготовителя,относят к изделиям вспомогательного производства.
ГОСТ 2.101-68устанавливает следующие виды изделий: 1)детали; 2)сборочные единицы; 3)комплексы; 4)комплекты. Из этого перечня рассмотрим два вида изделий.
Деталь – изделие, изготовленное из однородного по наименованию и марке материала без применения сборочных операций, но при необходимости с нанесением на него защитного или декоративного покрытия, а также изготовленное с применением местной сварки, пайки, склейки. Например: литой корпус; винт, подвергнутый хромированию; трубка, спаянная из одного куска листового материала; коробка, склеенная из одного куска картона.
Сборочная единица – изделие, составные части которого подлежат соединению между собой напредприятии-изготовителесборочными операциями (свинчиванием, прессовкой, сваркой, склеиванием, клепкой и т. п.). Например, сварной корпус, редуктор, станок.
Основным производственным документом, по которому изготовляют детали и собирают машины, возводят инженерные сооружения и строят здания, является чертеж. Чертеж является средством выражения замыслов конструктора или проектировщика. Виды и комплектность конструкторских документов на все изделия всех отраслей промышленности устанавливает ГОСТ2.102-68.
Чертеж детали – документ, содержащий изображение детали и другие данные, необходимые для ее изготовления и контроля.
Спецификация – документ, определяющий состав сборочной единицы, комплекса или комплекта.
Сборочный чертеж – документ, содержащий изображение сборочной единицы и другие данные, необходимые для ее сборки (изготовления) и контроля.
Чертеж общего вида – документ, определяющий конструкцию изделия, взаимодействие его основных частей и поясняющий принцип работы изделия.
Эскиз – чертеж, выполненный без применения чертежных инструментов
studfiles.net