Растровая развертка окружностей. Развертка окружности

Развёртка окружности - это... Что такое Развёртка окружности?

Развёртка окружности

Эвольвентой окружности является траектория любой точки прямой линии, перекатываемой по окружности без скольжения. По эвольвенте обрабатывают профиль зубьев зубчатых колёс. Эвольвенту окружности можно получить, сматывая натянутую нить с цилиндрической поверхности. Конец этой нити будет описывать эвольвенту.

Параметрические уравнения эвольвенты окружности:

где — радиус окружности; — угол поворота радиуса окружности.

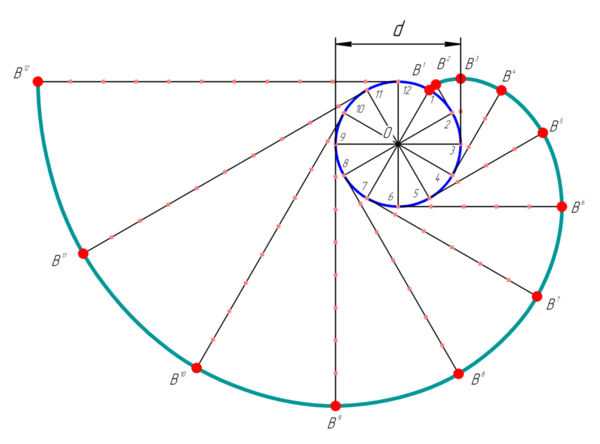
Построение эвольвенты окружности по заданному диаметру

Имеется окружность с диаметром , и с центром в точке . Данную окружность делим на двенадцать равных частей. В точках 2, 3, 4, … проводим касательные к окружности, направленные в одну сторону. Точки эвольвенты находим исходя из того, что при развёртывании окружности точка , должна отстоять от точки 2 на расстоянии, равном длине дуги между точками 1 и 2, а точка , должна отстоять от точки 3 на расстоянии, равном длине дуги между точками 1 и 3 (две длины предыдущей дуги), и т. д.

Точное положение точек эвольвенты получим, откладывая по касательным длины соответствующих дуг. Длину дуги между точками 1 и 2 определяем по формуле , где — диаметр окружности; — число частей, на которое разделена окружность.

Получив ряд точек эвольвенты соединяем их плавной линией.

В данном случае окружность с диаметром является эволютой к этой эвольвенте.

Эвольвента окружности

См. также

Литература

1. Богданов В. Н., Малежик И. Ф., Верхола А. П. и др. Справочное руководство по черчению.. — М.: Машиностроение., 1989. — С. 438-480. — 864 с. — ISBN 5-217-00403-7

Wikimedia Foundation. 2010.

Развёртка во времени
Развёртывание (технич.)

Смотреть что такое "Развёртка окружности" в других словарях:

Построение разверток тел вращения — Окружающий нас мир динамичен и разнообразен, и далеко не всякий объект можно просто обмерить линейкой. Для подобного переноса используются специальные техники, как то триангуляция. Потребность в составлении сложных развёрток, как правило,… … Википедия
МАСС-СПЕКТРОМЕТР — прибор для разделения ионизов. молекул и атомов по их массам, основанный на воздействии магн. и электрич. полей на пучки ионов, летящих в вакууме. В М. с. регистрация ионов осуществляется электрич. методами, в м а с с с п е к т р о г р а ф а х по … Физическая энциклопедия
Изгибаемый многогранник — Многогранник (точнее многогранная поверхность) называется изгибаемым, если его пространственную форму можно изменить такой непрерывной во времени деформацией, при которой каждая грань не изменяет своих размеров (то есть движется как твёрдое тело) … Википедия
Эвольвента — Эвольвенты окружности. Являются частью профиля в зубчатом колесе с эвольвентным зацеплением … Википедия
Масс-спектрометры — приборы для разделения ионизированных частиц вещества (молекул, атомов) по их массам, основанные на воздействии магнитных и электрических полей на пучки ионов, летящих в вакууме. В М. с. регистрация ионов осуществляется электрическими… … Большая советская энциклопедия
Сверлильный станок — станок для обработки отверстий со снятием стружки. На С. с. производят Сверление, Рассверливание, Зенкерование, Развёртывание, Растачивание, Нарезание резьбы. Различают следующие типы С. с. по металлу: вертикально сверлильные,… … Большая советская энциклопедия
Тетраэдр — (греч. τετραεδρον четырёхгранник) простейший многогранник, гранями которого являются четыре треугольника. У тетраэдра 4 грани, 4 вершины и 6 рёбер. Содержание 1 Связанные определения … Википедия
Открытые математические проблемы — Открытые (нерешённые) математические проблемы проблемы, которые рассматривались математиками, но до сих пор не решены. Часто имеют форму гипотез, которые предположительно верны, но нуждаются в доказательстве. В научном мире популярна… … Википедия
Теорема Линделёфа о многограннике — У этого термина существуют и другие значения, см. Теорема Линделёфа. Теорема Линделёфа о многограннике наименьшей площади при заданном объёме геометрическая теорема, впервые доказанная Лоренсом Линделёфом в 1869 году .[1]. Может быть… … Википедия

dic.academic.ru

Развертка окружности - это... Что такое Развертка окружности?

Развертка окружности

Параметрические уравнения эвольвенты окружности:

где — радиус окружности; — угол поворота радиуса окружности.

Построение эвольвенты окружности по заданному диаметру

Получив ряд точек эвольвенты соединяем их плавной линией.

В данном случае окружность с диаметром является эволютой к этой эвольвенте.

Эвольвента окружности

См. также

Литература

Wikimedia Foundation. 2010.

Развертка графа
Развернутый угол

Смотреть что такое "Развертка окружности" в других словарях:

Кривые* — Всякая линия, за исключением прямой, называется К. Если через все точки К. можно провести одну общую плоскость, то К. называется плоской. В противном случае К. называется К. двоякой кривизны. К. может быть рассматриваема или как геометрическое… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Кривые — Всякая линия, за исключением прямой, называется К. Если через все точки К. можно провести одну общую плоскость, то К. называется плоской. В противном случае К. называется К. двоякой кривизны. К. может быть рассматриваема или как геометрическое… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Построение разверток тел вращения — Окружающий нас мир динамичен и разнообразен, и далеко не всякий объект можно просто обмерить линейкой. Для подобного переноса используются специальные техники, как то триангуляция. Потребность в составлении сложных развёрток, как правило,… … Википедия
Винтовые линии движения и поверхности — Винтовые линии, цилиндрические и конические, суть кривые двоякой кривизны, начерченные первые на прямой круглой цилиндрической, а последние на прямой круговой конической поверхности и пересекающие прямолинейные производящие под постоянным для… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Винтовые линии, движения и поверхности — Винтовые линии, цилиндрические и конические, суть кривые двоякой кривизны, начерченные первые на прямой круглой цилиндрической, а последние на прямой круговой конической поверхности и пересекающие прямолинейные производящие под постоянным для… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
ГОСТ 16531-83: Передачи зубчатые цилиндрические. Термины, определения и обозначения — Терминология ГОСТ 16531 83: Передачи зубчатые цилиндрические. Термины, определения и обозначения оригинал документа: 5.3.1. Воспринимаемое смещение Разность межосевого расстояния цилиндрической зубчатой передачи со смещением и ее делительного… … Словарь-справочник терминов нормативно-технической документации
КАРТА — уменьшенное обобщенное изображение поверхности Земли (или ее части) на плоскости. Человек создавал карты с древнейших времен, пытаясь наглядно представить взаимное расположение различных участков суши и морей. Собрание карт, обычно переплетенных… … Энциклопедия Кольера
основная — 3.2 основная общеобразовательная школа: Школа, организуемая как самостоятельное общеобразовательное учреждение с 1 по 9 класс включительно. Источник: ТСН 31 328 2004: Общеобразовательные школы. Республика Саха (Якутия) Смотри также родственные… … Словарь-справочник терминов нормативно-технической документации
Маятник — М. называется тяжелое тело, совершающее колебания около неподвижной точки. Высокий интерес, представляемый движением М., замечен был впервые Галилеем, который усмотрел тесную связь между законами падения тел и законом качаний М. В 1657 г. Гюйгенс … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
легенда к географическим картам — НАСЕЛЕННЫЕ ПУНКТЫ :: более 1 млн. жителей :: от 250 тыс. до 1 млн. жителей :: от 100 тыс. до 250 тыс. жителей :: менее 100 тыс. жителей Прописными буквами выделены столицы. ПУТИ СООБЩЕНИЯ :: Железные дороги … Географическая энциклопедия

dic.academic.ru

Растровая развертка окружности. — КиберПедия

- окружность с центром в начале координат.

1 способ: - решение уравнения относительно y. Чтобы изобразить четвертую часть окружности, будем изменять x с единичным шагом от 0 до R и на каждом шаге вычислять y.

2 способ: использование вычислений x и y по формулам x=Rcosα, y=Rsinα при пошаговом изменении угла α от 0 до 90 градусов.

Окружность симметрична относительно координатных осей и прямых . В случае, когда центр окружности не совпадает с началом координат, эти прямые необходимо сдвинуть параллельно так, чтобы они прошли через центр окружности. Тем самым достаточно построить растровое представление для 1/8 части окружности, а все оставшиеся точки получить симметрией.

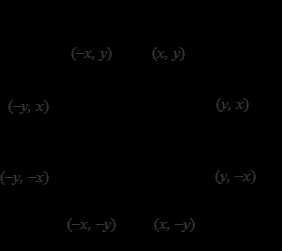
Алгоритм Брезенхейма (для участка окружности из второго октанта ).

Рассмотрим небольшой участок сетки пикселов, а также возможные способы (от A до E) прохождения истинной окружности через сетку (см. рис. ниже).

Предположим, что точка была выбрана как ближайшая к окружности при . Теперь найдем, какая из точек ( или ) расположена ближе к окружности при .

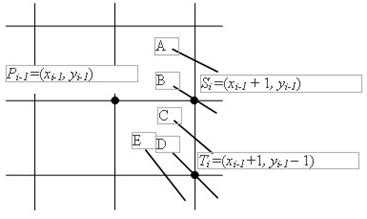
Заметим, что ошибка при выборе точки была равна .

Запишем выражение для ошибок, получаемых при выборе точки или :

, .

Если , то ближе к реальной окружности, иначе выбирается .

Введем .

Опуская алгебраические преобразования, запишем и для разных вариантов выбора точки или ( ):

Если выбирается ( ), то .

Закраска области, заданной цветом границы.

Рассмотрим алгоритм заполнения области с затравкой. В этих алгоритмах предполагается, что граница области задана на растровой плоскости и указана одна из внутренних точек области, которая называется затравочной. Требуется заполнить определенным цветом связную компоненту области, содержащую затравочную точку. Под связностью будем понимать 4-х или 8-ми связности, определенные выше.

Заполнение многоугольника.

Часто возникает задача заполнения многоугольников, заданных набором вершин.

Задача заполнения многоугольников решается в два этапа:

1) сначала проводится операция отсечения многоугольника;

2) затем производится заполнение полученных многоугольников.

Методы устранения ступенчатости.

Основная причина появления лестничного эффекта заключается в том, что отрезки, ребра многоугольника, цветовые границы и пр. имеют непрерывную природу, тогда как растровые устройства дискретны.

Метод увеличения частоты выборки.

Увеличение частоты выборки достигается с помощью увеличения разрешения растра. Таким образом учитываются более мелкие детали (размер картинки не меняется).

Метод, основанный на использовании полутонов.

В этом эвристическом методе интенсивность пикселя на ребре устанавливается пропорционально площади части пикселя, находящегося внутри многоугольника.

cyberpedia.su

Эвольвента (развертка) круга!

В близком родстве с архимедовой спиралью находится другая спираль — эвольвента круга (или эвольвента окружности). Это — линия, описываемая концом М (смотрите на рисунке) натянутой нити LM, сматываемой с круглой катушки D0LL1 (или наматываемой на катушку; в последнем случае точка М движется в обратном направлении). Геометрически указанное свойство выражается следующим образом.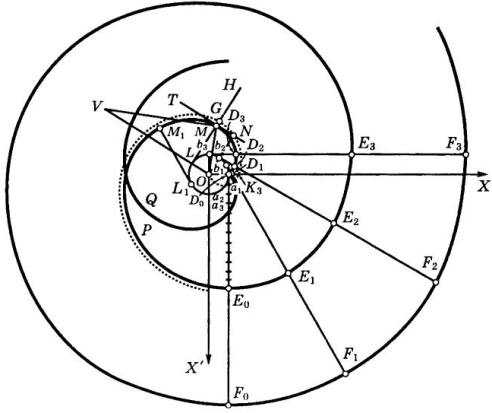Определение. Пусть точка L, исходя из начального положения D0, многократно описывает окружность радиуса k (k — параметр эвольвенты круга). На касательной LH откладывается по направлению, противоположному направлению вращения, отрезок LM, равный дуге D0L, пройденной точкой L. Эвольвента круга есть линия, описываемая точкой М. Одна и та же окружность имеет бесчисленное множество эвольвент (соответствующих всевозможным положениям начальной точки D0).

В зависимости от того, вращается ли точка L по часовой стрелке или в противоположном направлении, получаем правую эвольвенту круга (D0MP на рисунке) или левую (D0Q). Обычно две эвольвенты данного круга рассматриваются как две ветви одной линии.

Связь с архимедовой спиралью. Сопоставим правую (левую) ветвь эвольвенты круга с правой (левой) архимедовой спиралью с тем же параметром k = OD0 (т. е. с шагом 2πа =D0E0), что и эвольвента круга. Пусть эта спираль (пунктирная линия на рисунке) исходит из центра О данной окружности по направлению луча ОХ’, получаемого поворотом начального радиуса OD0 на угол -90° (+90°). Точка G, описывающая спираль, неограниченно приближается к эвольвенте: кратчайшее расстояние от точки G до эвольвенты (оно измеряется отрезком GM нормали LH эвольвенты) уже в конце первого витка составляет лишь 1% от шага спирали.

С другой стороны, полярный радиус ON спирали, составляющий угол -90° (+90°) с радиусом OL, имеет ту же длину kα , что отрезок LM. Это значит, что основание перпендикуляра, опущенного из центра О на касательную МТ эвольвенты у описывает архимедову спираль.

И на окончание небольшие исторические сведения. Эвольвенты различных линий впервые были изучены X. Гюйгенсом в его известной работе о часовом маятнике (1673 г.). Основные свойства эвольвенты круга найдены французским ученым Ла Гиром (1640—1718) и изложены в его работе 1706 г. Ещё некоторые А. К. Клеро (1713—1765) в 1740 г., а также кинематическое свойство натурального уравнения (любой линии) указаны Мангеймом в 1859 г.

Материалы по теме:

Поделиться с друзьями:

Загрузка...

matemonline.com

Растровая развертка окружностей

Четырехсторонняя симметрия

Рис. 3.7

Существует несколько простых, но не эффективных способов развертки окружности. Рассмотрим окружность с центром в начале координат:

Чтобы изобразить окружности, можно x с 0 до R и на каждом шаге вычислить y. Остальные четверти получаются симметричным отображением. Этот метод неэффективен, т.к. в него входят операции “ ” и “ ”. Более того, при значениях x близких к R в окружности появляются незаполненные промежутки. Можно было бы воспользоваться расчетом координат окружности, заданной в полярных координатах – , путем пошагового изменения от 00 до 900. Но недостатки остаются все те же.

Восьмисторонняя симметрия

Процесс преобразования окружностей в растровую форму можно улучшить, если полнее использовать симметричную окружности. Поэтому удобно вычислить значения окружности на дуге в 450, а потом симметрично отобразить их.

Алгоритм Брезенхэма для окружностей

Брезенхэм разработал пошаговый генератор дуг, который более эффективен, чем рассмотренные ранее. Необходимо сгенерировать только 1\8 часть окружности. Остальные части получаются путем отображения:

· 1-ой октант – отражение относительно y=x 1-го октанта;

· 2-ой квадрант – отражение относительно x=0 1-го квадранта;

· нижняя полуокружность – отражение относительно y=0 верхней полуокружности .

Рис. 3.8

Рассмотрим 1-ую четверть окружности с центром в начале координат. Начнем работу в т. x=0, y=R, окружность генерируется по часовой стрелке, y – монотонно убывающая функция аргумента x до т. .

Для любой заданной т. на окружности существует только 2 возможности выбрать следующий , наилучшим образом приближающий окружность.

Алгоритм выбирает , для которого минимален квадрат расстояния между одним из этих пикселов и окружностью.

Рис. 3.9

Вводится упрощающая переменная , значение которой можно вычислить в пошаговом режиме, используя лишь небольшое число сложений, вычитаний и сдвигов.

Возможно 7 способов прохождения истинной окружности через сетку. Пусть был выбран как ближайший к окружности при . Теперь найдем, какой из ( или ) расположен ближе к окружности при .

Рис. 3.10

Если , то ближе к окружности, чем .

Если , то ближе к окружности.

Введем упрощающую переменную :

Если

Для случаев 1,2: ( - внутри окружности)

( - внутри окружности)

Для случая 3: ( - внутри)

( - снаружи)

Для случаев 4,5: ( - снаружи)

( - снаружи)

После некоторых математических выводов было получено:

если ( ) если ( )

Растровая развертка окружности. - Программирование

- окружность с центром в начале координат.

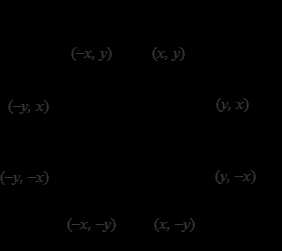
Алгоритм Брезенхейма (для участка окружности из второго октанта ).

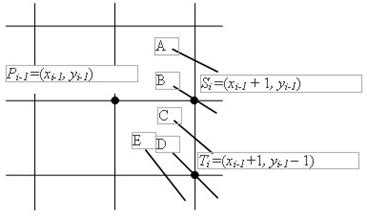
Заметим, что ошибка при выборе точки была равна .

Запишем выражение для ошибок, получаемых при выборе точки или :

, .

Если , то ближе к реальной окружности, иначе выбирается .

Введем .

Опуская алгебраические преобразования, запишем и для разных вариантов выбора точки или ( ):

Если выбирается ( ), то .

Закраска области, заданной цветом границы.

Заполнение многоугольника.

Часто возникает задача заполнения многоугольников, заданных набором вершин.

Задача заполнения многоугольников решается в два этапа:

1) сначала проводится операция отсечения многоугольника;

2) затем производится заполнение полученных многоугольников.

Методы устранения ступенчатости.

Метод увеличения частоты выборки.

Метод, основанный на использовании полутонов.

student2.ru

Растровая развертка окружностей

Существует несколько очень простых, но неэффективных способов преобразования окружностей в растровую форму. Рассмотрим для простоты окружность с центром в начале координат, для которой

x2+y2=R2. Решая это уравнение относительно у, получим

Y = ± 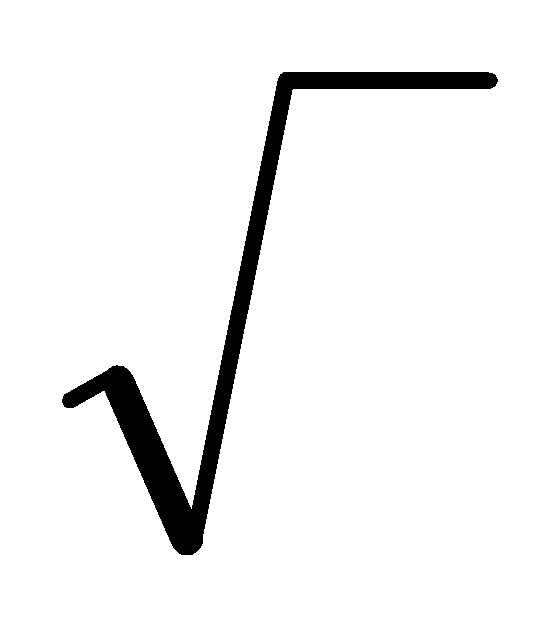R2 –x2

Чтобы изобразить четвертую часть окружности, можно увеличивать х с единичным шагом от 0 до R и на каждом шаге вычислять +у (остальные четверти изображаются симметрично).

Этот метод работоспособен, но не эффективен, поскольку в него входят операции умножения и извлечения квадратного корня. Более того, при значениях х, близких к R, в окружности появляются заметные незаполненные промежутки, так как при этих значениях х тангенс угла наклона касательной к окружности стремится к бесконечности (рис.).

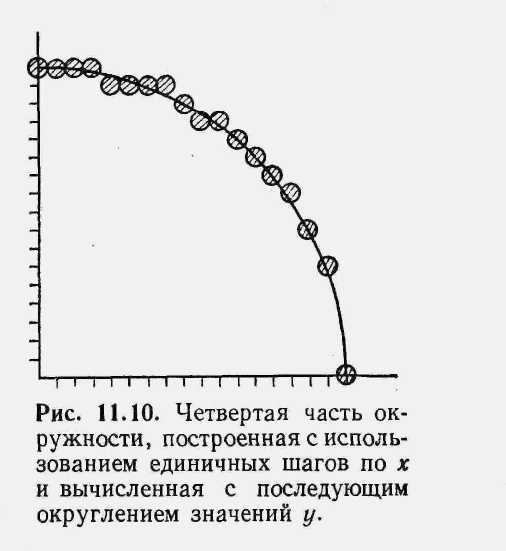
Неэффективным методом, при использовании которого также не удается избежать больших разрывов, является изображение R*cos или R*sin путем пошагового изменения от 0 до 900

Восьмисторонняя симметрия

Процесс преобразования окружностей в растровую форму можно улучшить, если полнее использовать симметрию окружности. Рассмотрим окружность с центром в начале координат. Если точка (х, у) лежит на окружности, очень просто вычислить семь других точек, принадлежащих окружности (рис.). Поэтому, если применять уравнение

Y = ± 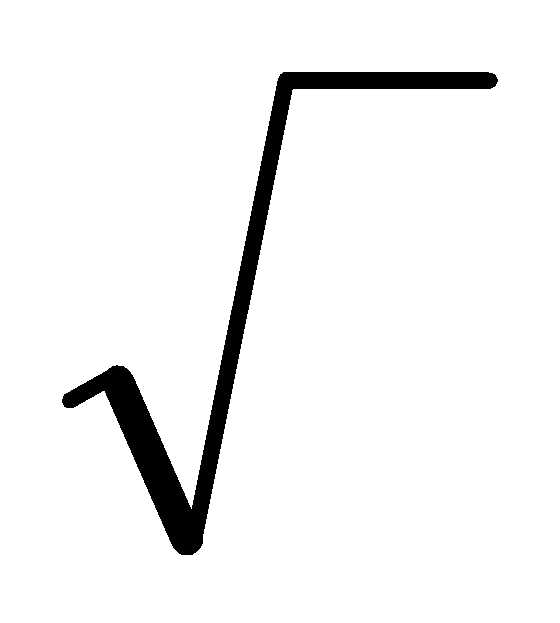R2 –x2

или некоторый другой более эффективный механизм вычисления у по значениям х из диапазона 0 — R/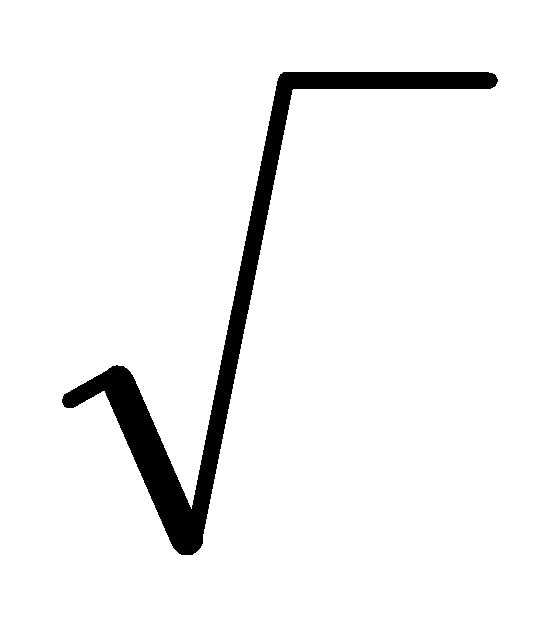2 (точка, в которой х = у) можно получить еще семь дополнительных точек на окружности. Этот диапазон х соответствует дуге окружности 45°, показанной на рисунке.

Алгоритм брезенхема для генерации окружности

В растр нужно разлагать не только линейные, но и другие, более сложные функции. Один из наиболее эффективных и простых для понимания алгоритмов генерации окружности принадлежит Брезенхему. Заметим, что необходимо сгенерировать только одну восьмую часть окружности. Остальные ее части могут быть получены последовательными отражениями, как это показано на рис. 2.10. Если сгенерирован первый октант (от О до 45° против часовой стрелки), то второй октант можно получить зеркальным отражением относительно прямой у=х, что дает в совокупности первый квадрант. Первый квадрант отражается относительно прямой х = 0 для получения соответствующей части окружности во втором квадранте. Верхняя полуокружность отражается относительно прямой у = 0 для завершения построения. На рис. 2.10 приведены двумерные матрицы соответствующих преобразований.

Для вывода алгоритма рассмотрим первую четверть окружности с центром в начале координат. Заметим, что если работа алгоритма начинается в точке х = 0, у = R, то при генерации окружности по часовой стрелке в первом квадранте у является монотонно убывающей функцией аргумента Х (рис. 2.11).

Отразить первый октант относительно Y= Х

0 1

1 0

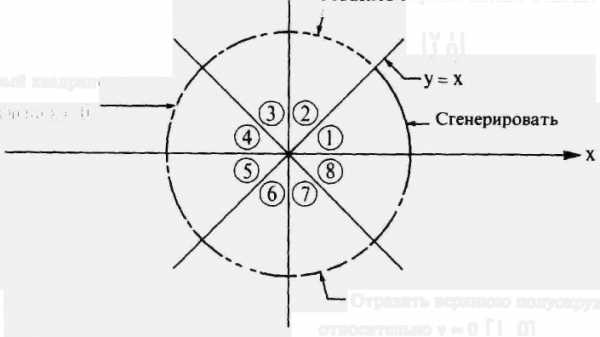
Отразить первый квадрант относительно х = 0

-1 0

0 1

Отразить верхнюю 1 0 полуокружность 0 -1 относительно У=0

Рис. 2.10. Генерация полной окружности из дуги в первом октанте.

Аналогично, если исходной точкой является у = 0, х = R , то при генерации окружности против часовой стрелки х будет монотонно убывающей функцией аргумента у. В нашем случае выбирается генерация по часовой стрелке с началом в точке х = 0, у = R . Предполагается, что центр окружности и начальная точка находятся точно в точках растра.

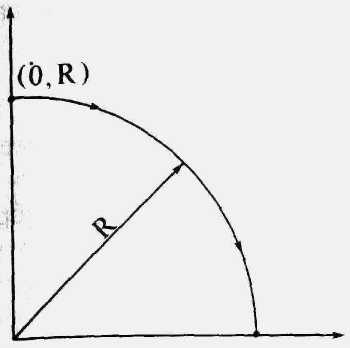
Рис. 2.11. Окружность в первом квадранте.

Для любой заданной точки на окружности при генерации по часовой стрелке существует только три возможности выбрать следующий пиксел, наилучшим образом приближающий окружность: горизонтально вправо, по диагонали вниз и вправо, вертикально вниз. На рис. 2.12 эти направления обозначены соответственно mH, mD, mV. Алгоритм выбирает пиксел, для которого минимален квадрат расстояния между одним из этих пикселов и окружностью, т. е. минимум из (здесь минимизируется не квадрат расстояния, а абсолютное значение разности квадратов расстояний от центра окружности до пиксела и до окружности)

mH = |(xi + 1)2 + (yi)2 – R2|

mD = |(xi + l)2 + (yi –l )2 - R2|

mV = |(xi)2 + (уi - 1)2 - R2|

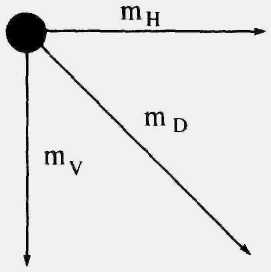
Рис. 2.12. Выбор пикселов в первом квадранте.

Вычисления можно упростить, если заметить, что в окрестности точки (xi, yi) возможны только пять типов пересечений окружности и сетки растра, приведенных на рис. 2.13.

Разность между квадратами расстояний от центра окружности до диагонального пиксела (xi + 1, уi - 1) и от центра до точки на окружности R2 равна

Di = (xi + 1)2 + (yi – 1)2 – R2

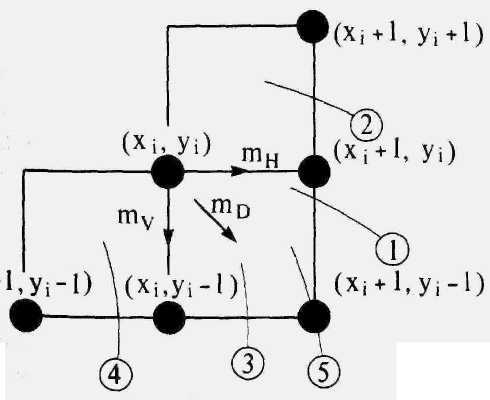
Рис. 2.13. Пересечение окружности и сетки растра.

Как и в алгоритме Брезенхема для отрезка, для выбора соответствующего пиксела желательно использовать только знак ошибки, а не ее величину.

A) При Di < 0

- диагональная точка (хi + 1, уi — 1) находится внутри реальной окружности, т. е. это случаи 1 или 2 на рис. 2.13. Ясно, что в этой ситуации следует выбрать либо пиксел (xi + 1, yi), т.е. mH, либо пиксел (xi + l, yi - 1), т. е. mD.

Для этого сначала рассмотрим случай 1 и проверим разность квадратов расстояний от окружности до пикселов в горизонтальном и диагональном направлениях:

d = |{(xi + I)2 + (уi)2 - R2}| - |{(xi + 1)2 + (уi - 1)2 - R2}|

При d < 0 расстояние от окружности до диагонального пиксела (mD) больше, чем до горизонтального (mH).

Напротив, если d > О, расстояние до горизонтального пиксела (mH) больше. Таким образом,

при d ≤0 выбираем mH в (хi + 1, уi)

при d > О выбираем mD в (xi + l, yi - 1)

При d = 0, когда расстояние от окружности до обоих пикселов одинаковы, выбираем горизонтальный шаг.

Количество вычислений, необходимых для оценки величины d, можно сократить, если заметить, что в случае 1

(xi + 1)2 + (yi)2 – R2  0

(xi + 1)2 + (yi - 1)2 – R2 < 0

так как диагональный пиксел (xi + 1, уi - 1) всегда лежит внутри окружности, а горизонтальный (xi + 1, уi) — вне ее.

Таким образом,  можно вычислить по формуле

 = (хi + 1)2 + (уi)2 - R2  (xi + 1)2 + (уi - 1)2 - R2

Дополнение до полного квадрата члена (уi)2 с помощью добавления и вычитания - 2уi + 1 дает

 = 2[(xi + 1)2 + (уi - 1)2 -R2] + 2yi – 1

В квадратных скобках стоит по определению i, и его подстановка

 = 2*(i + yi) - 1

существенно упрощает выражение.

Рассмотрим случай 2 на рис. 2.13 и заметим, что здесь должен быть выбран горизонтальный пиксел (хi + 1, уi,), так как y является монотонно убывающей функцией. Проверка компонент  показывает, что

(xi + 1)2 + (уi)2 - R2 < 0

(xi + 1)2 + (уi-1)2 - R2 < 0

поскольку в случае 2 горизонтальный (xi + 1, уi) и диагональный (хi + l, yi - 1) пикселы лежат внутри окружности.

Следовательно,  < 0, и при использовании того же самого критерия, что и в случае 1, выбирается пиксел (хi + 1,уi).

Б) Если i > 0,

то диагональная точка (хi + 1, yi — 1) находится вне окружности, т. е. это случаи 3 и 4 на рис. 2.13. В данной ситуации ясно, что должен быть выбран либо пиксел (xi + 1, yi — 1), т. е. mD, либо (xi, yi - 1), т. е. mV.

Аналогично разбору предыдущего случая, критерий выбора можно получить, рассматривая сначала случай 3 и проверяя разность между квадратами расстояний от окружности до диагонального mD и вертикального mV пикселов,

' = |{(xi + 1)2 + (yi - 1)2 - R2}| - |{(xi)2 + (уi - 1)2 - R2}|

При ' < 0 расстояние от окружности до вертикального пиксела (xi, yi — 1) больше и следует выбрать диагональный шаг mD, к пикселу (xi + 1, уi - 1).

В случае ' > 0 расстояние от окружности до диагонального пиксела больше и следует выбрать вертикальное движение к пикселу (xi, уi - 1).

Таким образом,

при ' ≤ 0 выбираем mD в (xi + 1, уi — 1)

при ' > 0 выбираем mVв (xi, уi — 1)

В случае ' = 0, т. е. когда расстояния равны, выбран диагональный шаг.

Проверка компонент ' показывает, что

(xi +1)2 + (yi - 1)2 – R2  0

(xi)2 + (yi – 1)2 – R2 < 0

поскольку для случая 3 диагональный пиксел mD (xi + l, yi — 1) находится вне окружности, тогда как вертикальный пиксел mV (xi, yi — 1) лежит внутри ее. Это позволяет записать ' в виде

' = (хi + 1)2 + (уi - 1)2 - R2  (xi)2 + (уi - 1)2 - R2

Дополнение до полного квадрата члена (хi)2 с помощью добавления и вычитания 2хi + 1 дает

' = 2[(xi + 1)2 + (уi - 1)2 - R2] – 2xi – 1

Использование определения i приводит выражение к виду

' = 2(i - xi) – 1

Рассматривая случай 4, снова заметим, что следует выбрать вертикальный пиксел (xi, yi - 1), так как у является монотонно убывающей функцией при возрастании х.

Проверка компонент ' для случая 4 показывает, что

(хi +1)2 + (yi - 1)2 -R2 > 0

(xi)2 + (yi – 1)2 – R2 > 0

поскольку оба пиксела находятся вне окружности.

Следовательно, ' > 0 и при использовании критерия, разработанного для случая 3, происходит верный выбор mV.

Случай 5, когда диагональный пиксел (xi + l, yi — 1) лежит на окружности, т. е. I = 0. Проверка компонент  показывает, что

(хi + 1)2 + (yi)2 –R2 > 0

(xi + 1)2 + (yi – 1)2 – R2 = 0

Следовательно,  > 0 и выбирается диагональный пиксел (xi + 1, уi — 1).

Аналогичным образом оцениваем компоненты ' :

(хi +1)2 + (уi - 1)2 - R2 = 0

(xi)2 + (уi - 1)2 - R2 < 0

и ' < 0, что является условием выбора диагонального шага к (хi + 1, уi -1)

Таким образом, случай I = 0 подчиняется тому же критерию, что и случай I< 0 или I > 0.

Подведем итог для полученных результатов:

I < 0

 ≤ 0 выбираем пиксел (xi + l, yi)  mH

I > 0

' ≤ 0 выбираем пиксел (xi + l, yi — 1)  mD

' > 0 выбираем пиксел (xi, yi - 1)  mV

I = 0 выбираем пиксел (xi + 1, уi - 1)  mD

Легко разработать простые рекуррентные соотношения для реализации пошагового алгоритма.

Рассмотрим горизонтальный шаг mH к пикселу (xi+1, у). Обозначим это новое положение пиксела как (i + 1). Тогда координаты нового пиксела и значение i равны

xi+1 = xi + 1

yi+1 = yi

i+1 = (xi+1 + 1)2 + (уi+1 - 1)2 - R2 =

= (xi+1)2 + 2xi+1 + 1 + (yi - 1)2 - R2 =

= [(xi + 1)2 + (yi – 1)2 – R2] + 2xi+1 +1 =

= I + 2xi+1 +1

Аналогично координаты нового пиксела и значение I для шага mD к пикселу (xi + 1, yi - 1) таковы:

xi+1 = xi + 1

yi+1 = yi - 1

i+1 = I + 2xi+1 -2yi+1 +2

То же самое для шага mV к (xi, уi - 1)

xi+1 = xi

yi+1 = уi - 1

i+1 = i - 2yi+1 + 1

studfiles.net

Растровая развертка окружностей. Развертка окружности

Развёртка окружности - это... Что такое Развёртка окружности?

Построение эвольвенты окружности по заданному диаметру

См. также

Литература

Смотреть что такое "Развёртка окружности" в других словарях:

Развертка окружности - это... Что такое Развертка окружности?

Построение эвольвенты окружности по заданному диаметру

См. также

Литература

Смотреть что такое "Развертка окружности" в других словарях:

Растровая развертка окружности. — КиберПедия

Эвольвента (развертка) круга!

Растровая развертка окружностей

Похожие статьи:

Растровая развертка окружности. - Программирование

Растровая развертка окружностей

Алгоритм брезенхема для генерации окружности