Построение проекции пирамиды. Развертка пирамиды начертательная геометрия
Начертательная геометрия
12.6. Развертки линейчатых поверхностей
Развертки конических, пирамидальных и других линейчатых поверхностей, за исключением цилиндрических, поверхностей строятся способом триангуляции (способом треугольников). Для построения разверток цилиндрических поверхностей данный способ хотя и применим, но не удобен.
Способ заключается в следующем: данная поверхность заменяется вписанной или описанной многогранной поверхностью с треугольными гранями и строится развертка этой многогранной поверхности.
Другими словами, построение разверток указанных поверхностей сводится к многократному построению натурального вида треугольников. Чем на большее количество треугольников разбита данная поверхность, тем точнее ее развертка.
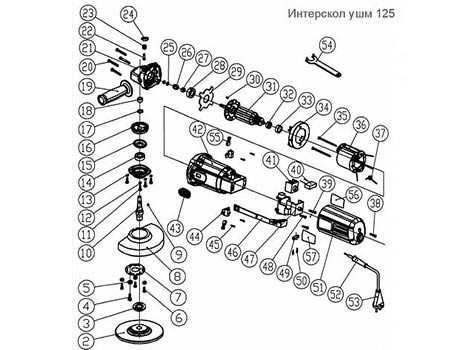
Рассмотрим применение этого способа для построения разверток пирамидальных поверхностей на примере наклонной пирамиды (рис. 157)
Грани пирамиды являются треугольниками, поэтому для построения ее развертки достаточно определить натуральные величины этих треугольников.
Для этого способом вращения вокруг горизонтально – проецирующей оси i(i1,i2) определены натуральные величины ребер:
Натуральная величина основания пирамиды определена способом замены плоскостей проекций:
После этого строится развертка боковой поверхности пирамиды и к ней пристраивается треугольник основания для получения полной развертки поверхности наклонной пирамиды. Положение точки S0 выбирается произвольно:
Также на рис. 157 показано построение с помощью прямой SD точки K, лежащей в грани SAB.
Рассмотрим построение разверток конических поверхностей. Для построения развертки способом триангуляции коническую поверхность заменяют вписанной в нее поверхностью пирамиды.
Подробнее рассмотрим применение этого способа для построения разверток конических поверхностей на примере эллиптического конуса с круговым основанием (рис. 158).
Рис. 157. Построение развертки наклонной пирамиды способом триангуляции
Рис. 158. Построение развертки наклонного конуса способом триангуляции
Коническая поверхность заменяется поверхностью вписанной шестиугольной пирамиды. Основание конуса точками I, II, III,… разбито на шесть частей. Так как коническая поверхность имеет плоскость симметрии α(α1)⊥ П1, то можно построить развертку только одной половины поверхности. Таким образом, поверхность разбита на ряд примыкающих один к другому треугольников с общей вершиной S: ∆ S-I-II, ∆ S-II-III, ∆ S-III-IV,…Каждый из этих треугольников строится по трем сторонам, при этом две стороны равны натуральным величинам образующих, а третья – хорде, стягивающей дугу окружности основания между соседними точками деления. Для определения натуральных величин этих треугольников способом вращения вокруг оси i(i1,i2) построены натуральные величины их сторон – образующих конуса:
Стороны I–II, II–III, III–IV,…изображаются на П1 в натуральную величину, так как основание конуса лежит в горизонтальной плоскости уровня.
Для построения развертки положение точки S0 выбирается произвольно, а каждый треугольник строится по трем сторонам:
После этого построена развертка боковой поверхности конуса – фигура S0–I0–II0–…–I0, при этом точки I0, II0,…I0 соединены плавной кривой линией, являющейся разверткой окружности основания.
cdot-nntu.ru
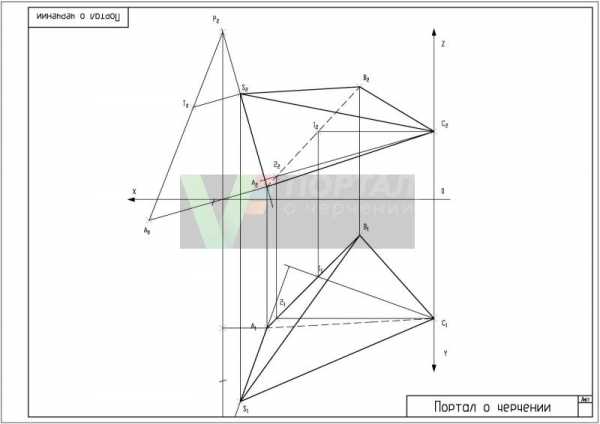
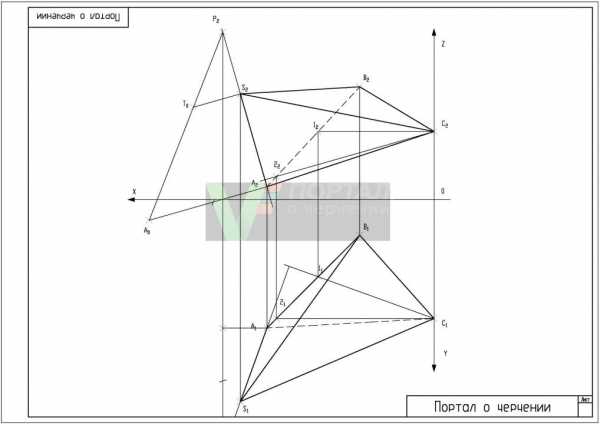
Построение проекции пирамиды
Дано:Таблица значения координат основания ABC прямоугольной пирамиды. Значение высоты h прямоугольной пирамиды SABC
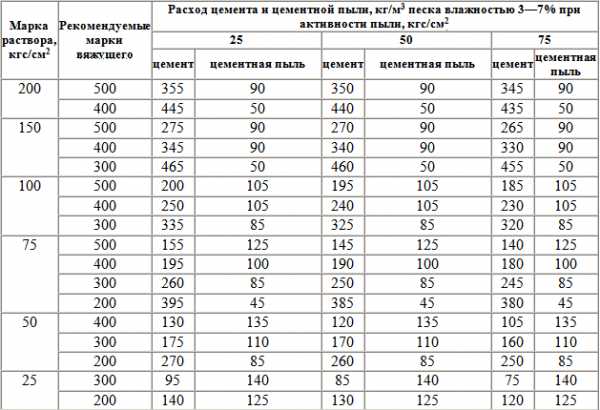
| Вариант | XA | YA | ZA | XB | YB | ZB | XC | YC | ZC | h |
| 1 | 117 | 90 | 9 | 52 | 25 | 79 | 83 | 48 | 85 |
Необходимо: Построить проекции пирамиды
Решение задачи на построение проекции пирамиды схоже с решением задачи на построение плоскости параллельной заданной.
Алгоритм решение задачи по начертательной геометрии на построение проекции пирамиды:
Подробнее в видеоуроке по начертательной геометрии в Автокад.
Автор:
Построение проекции пирамиды
P.S.
Этот видеоурок и статья входят в профессиональный бесплатный самоучитель Автокад, который подходит как для начинающих пользователей, так и уже давно работающих в Автокад.Тематика писем:
Выберите из спискаВсе статьиAutoCAD 2DAutoCAD 3DAutoCAD Architecture КомпасInventor3D maxRevitОсновы черченияНачертательная геометрияИнженерная графикаМашиностроительное черчениеСтроительное черчениеСхемы
drawing-portal.com
Способ построения проекции перпендикуляра. Развертка пирамиды методом треугольников
Вопрос №9
Способ построения проекции перпендикуляра, опущенного из точки М на треугольник общего положения АВС
Пример 2. Задана точка D и проекции треугольника АВС. Требуется определить расстояние от точки D до плоскости треугольника АВС.
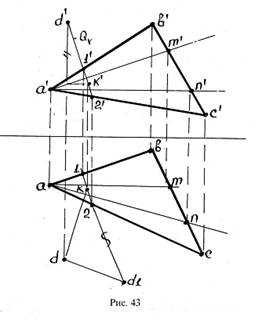
Решение: Из точки D опускается перпендикуляр на плоскость треугольника АВС. Для построения проекций перпендикуляра используются горизонталь и фронталь треугольника АВС (АМ, AN, рис. 43).
Определяется точка встречи перпендикуляра с плоскостью треугольника АВС. С этой целью через фронтальную проекцию перпендикуляра проводится вспомогательная фронтально-проектирующая плоскость Q. Эта плоскость пересекает стороны треугольника АВС в точках 1, 2 (см. рис. 43).
На горизонтальной проекции определяется точка пересечения перпендикуляра с линией 1-2 (точка k, см. рис. 43).
Определяется натуральная величина отрезка DК, которая представляет расстояние от точки D до плоскости треугольника АВС.
Вопрос №10
Построение сечения поверхности плоскостью общего положения методом ребер. Привести пример.
Вопрос №31
Развертка пирамиды методом треугольников. Пояснить на примере.
Рассматривается пример построения линии пересечения пирамиды плоскостью общего положения Р (рис. 73 а).
Через ребро SC проводится горизонтально – проектирующая плоскость Q и определяется линия пересечения плоскостей P и Q – линия 1 –2.
На фронтальной проекции определяется точка пересечения линии 1¢ - 2¢ с ребром S¢C¢ - точка m¢ (см. рис 73 а).
Через ребро sb проводится проектирующая плоскость S и определяется линия пересечения плоскостей S и Р – линия 3 – 4. Находится точка пересечения линии 3¢ - 4¢ с ребром s¢b¢ - точка n¢.
Через ребро s¢a¢ проводится фронтально – проектирующая плоскость R и строится линия пересечения плоскостей R и Р – линия 5 – 6. Определяется точка пересечения линии 5 - 6 с ребром sa – точка К.
На горизонтальной и фронтальной проекциях точки KMN соединяются прямыми. В результате построения получают проекции сечения пирамиды плоскостью.
Развертка пирамиды выполняется способом прямоугольников. Вначале определяются натуральные размеры ребер пирамиды способом плоско – параллельного перемещения: точка S перемещается параллельно оси Х в положение S1 (см. рис. 72 а). Прямая SA разворачивается вокруг точки S1 до положения, когда она станет параллельной оси Х – положение s1a1. Аналогично определяются положения ребер s1b1и s1c1.
Определяются фронтальные проекции точек SABC - s¢1, a¢1, b¢1, c¢1. Соединив вершину s¢1 с точкой основания пирамиды, получают натуральные величины ребер s¢1 a¢1, s¢1 b¢1, s¢1 c¢1.
На полученные линии проектируются точки k¢, n¢, m¢ - k¢1, n¢1, m¢1.
Развертка пирамиды выполняется путем последовательного построения ее граней, совмещенных с плоскостью проекции:
Проводится базовая линия. На ней отмечаются точки S и А. Размер отрезка SA снимается с фронтальной проекции - s¢1 a¢1.
Строится грань SAB – из точки S радиусом R1 = s¢1 b¢1 строится дуга окружности. Из точки А радиусом r1 = sa наносится вторая дуга окружности. Пересечение двух дуг окружностей определяет положение точки В.
vunivere.ru
|
онлайн Чтобы развертка поверхностей осуществлялась, их необходимо представлять как гибкую, нерастяжимую пленку. Представленные таким образом поверхности можно путем распрямления совместить с плоскостью. Если отсек поверхности может быть совмещен с плоскостью без разрывов, то такую поверхность называют развертывающейся, а полученнуюплоскую фигуру - ее разветкой. Поверхности, которые не могут быть совмещены с плоскостью из-за разрывов, относятся к неразвертываемым поверхностям. К группе для которой возможна развертка поверхностей могут быть отнесены только линейчатые поверхности и, в частности, те из них, которые имеют пересекющиеся смежные образующие. Точка пересечения может быть собственной - поверхности с ребром возврата и конические, и несобственной - поверхности цилиндрические. Рассмотрим развертывание конической поверхности α на плоскость β 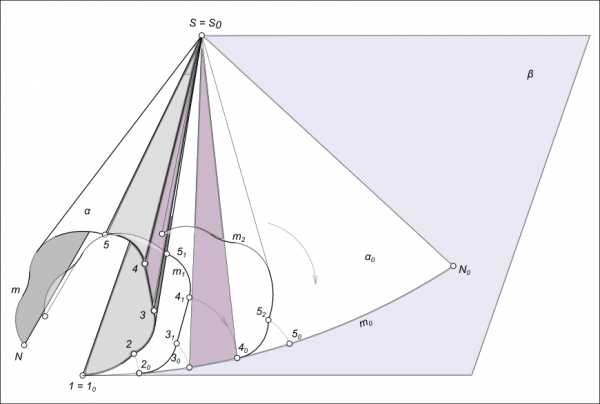 Развертка поверхностей Развертка поверхностей сопровождается постепенным спрямлением поверхности α и ее совмещением с плоскостью β, касательной к ней. Линия касания - образующая 1S. Проведем из точки 2, на направляющей конической поверхности m, образующую конической поверхности 2S. Если расстояние между точками 1 и 2 мало, то Δ1S2 можно с определенной степенью точности отождествлять с отсеком конической поверхности, заключенной между образующими 1S и 2S. Поворачивая Δ1S2 вокруг стороны 1S до его совмещения с плоскостью β, получим Δ1S20, представляющий развертку отсека поверхности α 1S2 на плоскость β. При перемещении точки 2 в положение 20 направляющая конической поверхности m займет положение m1. Проведя такие же действия к точкам 3; 4; ...; N получим развертку поверхности α на плоскость β. Развертка поверхностей представлена в следующих статьях: Графическая работа 7 - призма и пирамида; Графическая работа 8 - развертки поверхностей вращения цилиндра и конуса Графическая работа 12 - развертки поверхности усеченной пирамиды. Графическая работа 13 - развертки поверхности усеченного прямого кругового конуса. Графическая работа 14 - развертки боковой поверхности конуса. + |
ngeo.fxyz.ru
Начертательная геометрия: решение задач 1 курса
Предмет начертательной геометрии
Начертательная геометрия – одна из фундаментальных дисциплин инженерного образования, где пространственные фигуры изучаются по их проекционным изображениям. Основной целью данной дисциплины является разработка методов изображения геометрических фигур на плоскости или на другой поверхности и дальнейшее их применение при решении задач.
Методы начертательной геометрии позволяют с высокой степенью точности решать математические задачи графически. В изобразительном искусстве, архитектуре и строительстве метод проекций позволяет получать наглядные изображения создаваемых объектов.
Задачи начертательной геометрии решаются графическим путем. Знание базовых правил и теорем позволяет решать сложные задания путем расчленения процесса их решения на ряд элементарных однотипных операций. Основополагающей операцией, которую приходится выполнять в процессе решения, является определение точки пересечения двух линий.
Начертательная геометрия является одним из лучших средств развития у человека пространственного воображения, логического мышления, без которых сложно представить любое инженерное творчество.
Основные виды задач
Метрическими называются задачи, в которых требуется определить действительные значения величин плоских фигур, углов, отрезков, расстояний или построить геометрические объекты заданных размеров.
В общем случае геометрические фигуры произвольно расположены по отношению к плоскостям проекций и проецируются на эти плоскости с искажением их линейных и угловых величин. Чтобы определить натуральную величину любой плоской фигуры, ее нужно перевести в положение, при котором она будет параллельна одной из плоскостей проекций.
Позиционными называются задачи, в которых требуется определить взаимное положение геометрических объектов – построить линию их пересечения или определить принадлежность точки некоторой фигуре. Для решения позиционных задач обычно используют ряд вспомогательных поверхностей. Их выбирают таким образом, чтобы они пересекались с заданными фигурами по линиям, которые просты для построения – например, по прямым и окружностям.
В начертательной геометрии существуют базовые задачи, без освоения которых невозможно дальнейшее изучение предмета. Это построение ортогональных проекций точек и поверхностей, определение следов прямых и плоскостей. Владение методами преобразования проекций позволяет самостоятельно анализировать и значительно упрощать решение многих задач.
ngeometry.ru